基于线性补偿方式的电磁式CT负荷特性的研究

张杰梁

（福建省计量科学研究院，福建 福州 350003）

基于线性补偿方式的电磁式CT负荷特性的研究

张杰梁

（福建省计量科学研究院，福建 福州 350003）

为分析二次负荷对电磁式电流互感器误差的影响，利用电流互感器的T型等效电路建立未经补偿电磁式电流互感器误差的数学模型,通过实验得出其负荷特性试验数据，进而拟合出负荷特性曲线。在分析各检定规程对电流互感器负荷箱计量性能要求的基础上，采用OMICRON公司的CT分析仪对两种不同相数和线圈外绝缘介质的电磁式电流互感器进行负荷特性试验。结果表明：高压电磁式电流互感器对二次负荷并不敏感，当负荷误差在-13%～13%变化时，比值差和相位差的变化还不到一个修约间隔；而对低压电磁式电流互感器而言，比值差最大变化超过1个修约间隔。

电流互感器；负荷特性；线性补偿；非线性补偿

0 引 言

虽然电流负荷在电磁式电流互感器的检定中仅扮演配套设备的角色，但由于电磁式电流互感器的准确度与负荷有关，若检定时的实际负荷与铭牌上标注的二次负荷差异过大，将对被检电磁式电流互感器产生明显的容量变化，影响测量结果的准确度与可靠性。

文献[1]～[5]提出了二次负荷对电流互感器误差的重要影响，但均未对不同补偿方式、不同相数以及采用不同的绝缘介质的电流互感器负荷特性进行比较分析。考虑到目前国内广泛使用的电磁式电流互感器，其准确度一般为0.1级及以下等级，这类电流互感器采用的铁心一般为冷轧硅钢片，普遍采用线性补偿方式，如匝数补偿、分数匝补偿等。0.05级及以上的精密电流互感器主要在一些特殊场合下使用，如在电流互感器检定装置中作为主标准器用来检定低等级的电流互感器，此时，其误差负荷特性往往因采用多种非线性补偿方式而不具备规律性。故本文的研究工作主要针对线性补偿方式的电磁式电流互感器展开。

首先分析了未经补偿电磁式电流互感器的误差形成机理及负荷特性，在此基础上以线性补偿方式的电磁式电流互感器为例，对其上下限误差特性曲线进行分析。同时在给出国内各检定规程对电流互感器负荷箱的计量性能要求的前提下，基于OMICRON公司的CT分析仪，对相数采用支柱式和母线式、线圈外绝缘介质采用绕组浇注成型固体和塑料壳的电力系统用电流互感器的误差负荷特性进行试验分析[6-7]。

1 未经补偿电磁式电流互感器的误差形成机理及负荷特性

未经补偿的的电磁式电流互感器，其等值电路如图1所示。图中，二次电流通过外接负荷阻抗Z，产生二次压降通过绕组内阻抗产生电压降二次回路的总阻抗为[8]

式中：B——磁密，T（1T=10000Gs）；

S——铁心截面，cm2；

k——铁心叠片系数，目前电磁式电流互感器通常采用的冷扎硅钢片k=0.9～0.95。

要使铁心有磁密B，铁心必须有磁场强度H，磁密和磁场强度的比值就是铁心的磁导率，一般用μ表示。

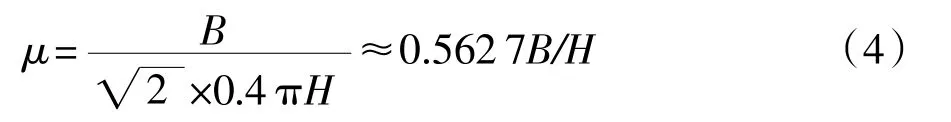
图1 未经补偿的电磁式电流互感器等值电路图

由于电流互感器的复数误差，是反转180°的二次电流相量按额定电流比折算至一次后，与实际一次电流相量之差对实际一次电流的比值，并用百分数表示[9]，即：

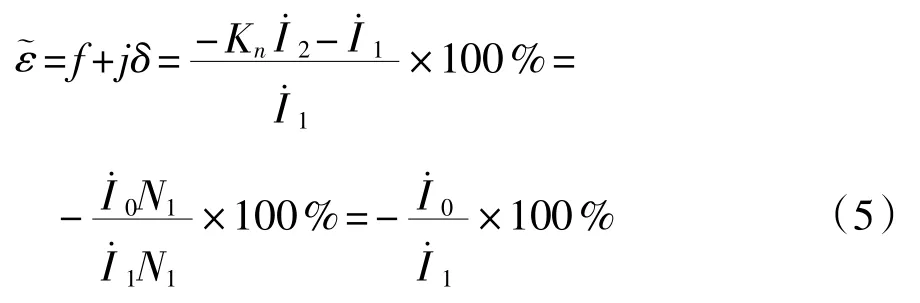
即复数误差为二次负荷与二次励磁阻抗之比的负值。

联立式（2）、式（3）、式（7），并将I1W1=I2W2代入，可得电流互感器的误差计算公式：

式中：Z2——二次回路的总阻抗；

l——铁心的平均磁路长度；

W——二次绕组匝数；

μ——铁心磁导率；

S——铁心截面积；

k——铁心叠片系数。

由式（7）可知，电流互感器的误差与二次负荷的大小成正比。当二次负荷增大时，铁心的磁密增大，铁心的磁导率也略有增大，所以互感器的误差随着二次负荷的增大而增大，但小于正比的增大[10]。

2 基于线性补偿方式的电磁式电流互感器上下限负荷误差特性曲线的分析

为了分析基于线性补偿方式的电磁式电流互感器上下限误差特性曲线，以未经补偿的电磁式电流互感器为例，对其额定变比500A/5A时的负荷特性进行试验（试验结果见表1），从表1可知，该电磁式电流互感器的基本误差不符合0.1级要求。为提高其准确度等级，需对其误差进行补偿，考虑到其比值差总体偏负，故可采用匝数补偿的方式对二次绕组少绕一匝，此时比值差补偿量Δf=W×100/W2=1.00%，相位差补偿量Δδ=0.00%，经补偿后的数据如表2所示。从表2可以看出，匝数补偿起到了平移比值差曲线的作用。经过线性补偿后的电流互感器，其准确度可达到0.1级，现采用Matlab进行二次拟合。图2为电磁式电流互感器负荷误差特性曲线，从图2（a）～（f）可以看出，功率因数相同时，额定负荷的误差（包括比值差和相位差）大于下限负荷的误差，且二者的比值差（相位差）曲线随着电流的增大而增大（减小），当增大到100%额定电流时，互感器接近饱和，此时误差曲线不再按比例增加（减小）；当负荷相同时，在功率因数1.0时的比值差较0.8时小，而相位差则相反。值得一提的是，当电磁式电流互感器采用匝数补偿方式或分数匝补偿方式进行误差补偿时，其比值差虽然减小了，但二次负荷对误差的影响趋势没有发生变化。此外，不同厂家生产的不同型号电磁式电流互感器，虽误差不同，但上下限负荷误差特性曲线大致相同。

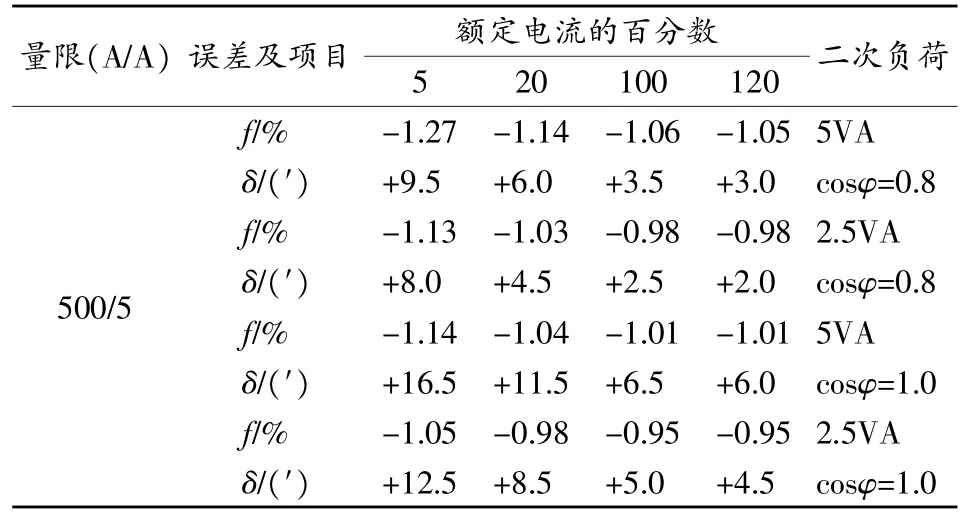
表1 未经补偿电流互感器负荷特性试验结果

表2 经匝数补偿后电流互感器负荷特性试验结果

3 CT二次负荷计量性能要求及误差负荷特性影响试验

3.1 各检定规程对电流互感器负荷箱的计量性能要求

目前涉及电流互感器负荷箱的规程主要有JJG 313—2010《测量用电流互感器检定规程》、JJG 1021—2007《电力互感器检定规程》以及JJG 1264—2010《互感器负荷箱校准规范》。JJG 313—2010《测量用电流互感器检定规程》和JJG 1264—2010《互感器负荷箱校准规范》对电流互感器负荷的误差要求基本是一致的，JJG 1021—2007《电力互感器检定规程》主要针对现场电流互感器的检定，其参考气温为-25～55℃，此时要保证负荷箱的最大相对误差达到±3%级就比较困难[11]。因此该规程将负荷箱在80%～ 120%范围内的有功和无功分量相对误差规定为不超过±6%，在其他有规定的电流百分数下，不超过±9%。此外，为了考虑电阻受温度的影响，JJG 313—2010《电流互感器检定规程》和JJF 1264—2010《互感器负荷箱校准规范》增加了温度附加误差，即周围温度每变化10℃时，负荷的误差变化不超过±2%。此时，若环境温度在10～35℃时，允许误差变化为±5%[12]。

3.2 电磁式电流互感器误差负荷特性影响试验及分析

不同的规程规范在不同温度类型和额定电流百分值下的计量性能要求是不同的。现以LZZBJ9-10h1型高压电磁式电流互感器和LMK-0.66型低压电磁式电流互感器为例，采用OMICRON公司的CT分析仪对二者在额定电流百分值为100%时的负荷误差影响进行试验，试验结果如表3和表4所示。

试验数据表明：高压电磁式电流互感器对二次负荷并不敏感，当负荷误差在-13%～13%变化时，比值差和相位差的变化还不到一个修约间隔；而对低压电磁式电流互感器而言，比值差最大变化为0.24%，超过1个修约间隔。

表3 LZZBJ9-10h1型高压电磁式电流互感器负荷误差试验结果

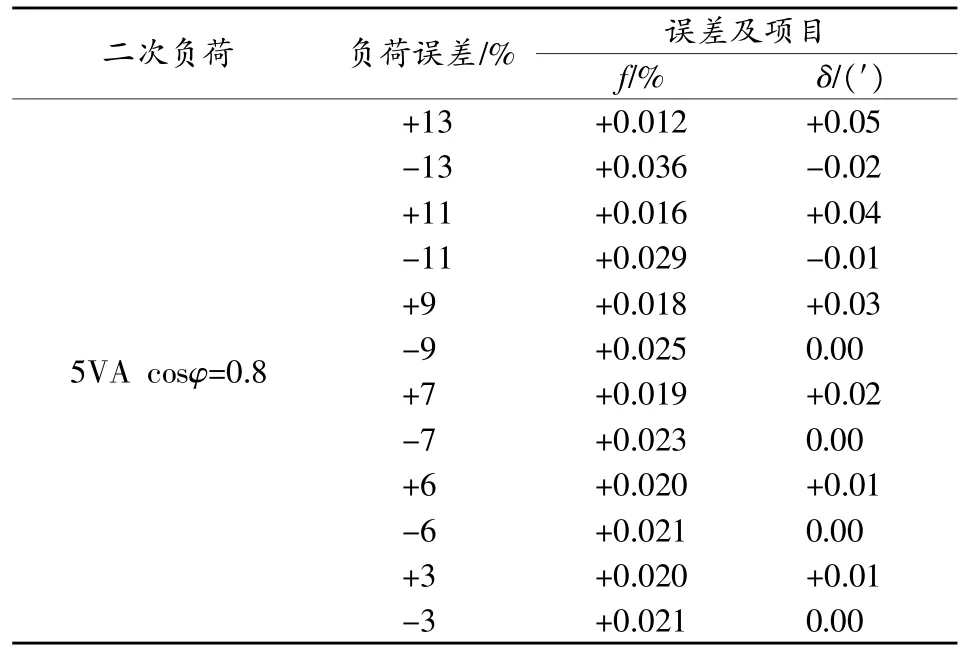
表4 LMK-0.66型低压电磁式电流互感器负荷误差试验结果

图2 电磁式电流互感器负荷误差特性曲线

4 结束语

无论是基于线性补偿方式还是非线性补偿方式的电磁式电流互感器，其二次负荷对测量结果的影响都是相当大的，基于线性补偿方式的电磁式电流互感器的误差随着二次负荷的增大而增大，但小于成正比的增大。当二次负荷的功率因数角φ增大时，将引起互感器的比值差增大，相位差减小。而基于非线性补偿方式的电磁式电流互感器的误差负荷特性不具备规律性。

型号不同，基于线性补偿方式的电磁式电流互感器其误差负荷特性曲线大致相同，而基于非线性补偿方式的电磁式电流互感器因其补偿方式不尽相同故其误差负荷特性曲线往往差异较大。

高压电力用电流互感器对二次负荷并不敏感当负荷误差在-13%～13%变化时，误差变化还不到一个修约间隔，但这并不意味着二次负荷对电流互感器误差的影响可以忽略。实际上，高压电磁式电流互感器一般用于电力系统中，二次负荷与现场的其他因素如邻近载流导体、环境电磁场干扰、环境温度、相对湿度等可能对测量结果带来更大的误差，故二次负荷应在满足一定的准确度要求，从而保证电磁式电流互感器测量结果的可靠性和准确性。

[1]JJG 1264—2010互感器负荷箱校准规范[S].北京：中国计量出版社，2010.

[2]赵屹涛，赵修民.升压升流器与负荷箱[M].北京：中国水利水电出版社，2005：91-112.

[3]赵修民.在互感器检定中负载误差所造成的影响[J].互感器通讯，1993（4）：1-5，22.

[4]吴丽静.二次压降和二次负荷对电能计量准确度的影响[J].电测与仪表，2007（3）：38-39.

[5]唐国民，秦富祥，王郁，等.电流互感器标准装置中二次负荷检测方法探讨[J].中国测试，2013（7）：22-25.

[6]张杰梁.数字式互感器校验仪误差频率特性的试验分析及改善[J].工业计量，2013（1）：12-15.

[7]张杰梁.电磁式电压互感器检定方法综述 [J].机电技术，2012（6）：90-92.

[8]赵修民.电流互感器[M].太原：山西科学教育出版社，1990：31-38.

[9]刘庆余.电流互感器的补偿方法及电流比较仪在电流互感器校验中的应用[J].电测与仪表，1981（8）：1-7.

[10]张杰梁，黄洪，方杰.电流互感器负荷箱的检测及误差分析[J].计量技术，2010（12）：38-40.

[11]王榕模，张杰梁，陈丹英.电流互感器现场校验仪校准方法研究[J].计量技术，2012（3）：52-55.

[12]张杰梁.电流互感器现场测试仪校准方法研究[D].厦门：厦门大学，2011.

[13]Kusters N L，Moore W J M.A phantom burden for currenttransformer[J].IEEE Trans on Instrumentation and Measurement，1969，1（18）：261-265.

Research on error characteristic changing with burden for CT with linear compensation style

ZHANG Jie-liang
（Fujian Institute of Metrology，Fuzhou 350003，China）

Mathematicalmodelofuncompensated CT based on T equivalentcircuits was established to analyze the CT error characteristic.Then the error characteristics changing with burden were obtained by experiment and simulation software MATLAB.Finally，the results were gotten by analyzing CT error characteristic with CT analyzer under the performance requirements of burden box of CT in calibration specification or verification regulation.The results show the error of high-voltage CT is not sensitive to the burden.When the load error in the range from-13% to 13%and the low-voltage CT，the ratio difference the biggest change more than 1 rounding interval.

current transformer；error characteristic changing with burden；linear compensation；nonlinear compensation

TM933.1；TM934.43；TM714；TM930.114

：A

：1674-5124（2014）05-0040-04

10.11857/j.issn.1674-5124.2014.05.010

2013-11-05；

：2013-12-28

张杰梁（1981-），男，福建莆田市人，工程师，硕士，主要从事电磁计量测试技术的研究。