换电模式下电动汽车供能网络的全寿命周期成本规划

徐婧劼，肖 贤，范镇南

（1.国网四川省电力公司技能培训中心，成都610000；2.国网内江供电公司，内江641003；3.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400030）

电动汽车EV（electric vehicle）由于使用电力驱动避免了石油燃料消耗，减少了对环境的污染，正逐步受到人们的关注。目前，多数发达国家已经初步形成了电动汽车的规模市场[1]，我国也颁布了《节能与新能源汽车产业规划（2012—2020）》。电动汽车将有着巨大的发展潜力[2]。

电动汽车的快速发展要求其供能的便捷性与经济性，而供能网络的规划建设基于供能模式的选择。文献[3]指出在国外电动汽车在能源供给模式的选择方面充电仍是主导，换电发展相对滞后；文献[4]提出了我国纯电动汽车可以根据不同车型采用电池租赁或整车充电，以及2 种方式相结合的模式；文献[5-6]研究了研究电动汽车充电站的规划与定容；文献[7]研究了在配电网规划的同时进行充电站的选址定容规划；文献[8]研究了电动汽车换电模式下供能网络的规划模型。目前，对于充电模式研究较多且比较深入，而换电模式的研究相对较少[9]，特别是对于换电网络规划考虑的因素不够全面，规划方法单一，没有把集中型充换电站和换电站作为整体考虑。

本文基于国家电网提出的“集中充电，统一配送”思想，研究了换电模式下供能网络的规划问题，将集中型充换电站和换电站作为整体考虑，引入全寿命周期成本LCC（life cycle costing）理论进行建模，结合泰森多边形和量子差分算法QDEA（quantum and differential evolution algorithm）对模型求解，提出电动汽车供能网络的近期规划方案，并展望到远期全寿命周期结束。

1 换电模式下供能网络规划思路

“集中充电，统一配送”是换电模式的典型代表，其供能网络主要包括集中型充换电站和换电站。集中型充换电站不仅需要为电动汽车换电，而且需要对所有电池进行充电，并通过配送车辆将电池配送到换电站；换电站只需要为电动汽车换电，不承担电池充电任务，在选址方面具有一定的灵活性。

所以，在进行供能网络规划时，首先应该通过专家经验对集中充换电站站址进行预选，形成待选站址集合（此时着重考虑有条件的公交车站，因为公交车行业是最容易推广电动汽车的行业，也是换电需求较大的行业）；然后依据近期电动汽车保有量确定站内主要设备的数量，依据远期全寿命周期结束时的保有量确定各站的占地面积；最后，从用户便捷性，整体供能网络经济性来确定集中充换电站和换电站的近期规划方案。这样既保证了各集中充换电站在寿命周期内有条件扩建，在未来增加换电站布点时又能实现供能网络的平滑过渡。

2 供能网络的全寿命周期成本规划模型

为了使模型简单化，建模时只考虑2 种类型的车辆，即大型车辆和小型车辆。大型车辆主要指公交车等配置电池较多的车辆，小型车辆主要指小轿车等配置电池较少的车辆。

2.1 规划目标年电池数量预测

在换电模式下，需要配置的电动汽车电池数量较大，由于目前电池的价格也比较昂贵，所以合理地配置电动汽车电池数量对控制整个供能网络的成本具有重要意义。

本文通过电动汽车的保有量和日均换电池数量来确定需要配置的电池数，日均换电池数可以通过日行驶里程来计算。则第i 个充换电站需要配置的电池数为

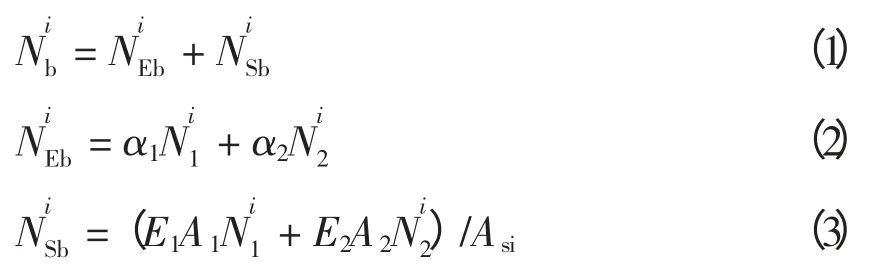
根据待规划城市各分区在目标年2 类采用换电模式的电动汽车数量及相关的运行参数，就可以确定各集中充电站需要配置的电池数量，为下一步设备需求计算做准备。

2.2 集中型充换电站与换电站的设备需求计算

集中型充换电站的主要设备包括电池充电设备（包含监视保护设备）、电池换电设备、配送车辆和叉车，换电站的主要设备包括电池换电设备和叉车。充换电站相应的配置需求计算公式为

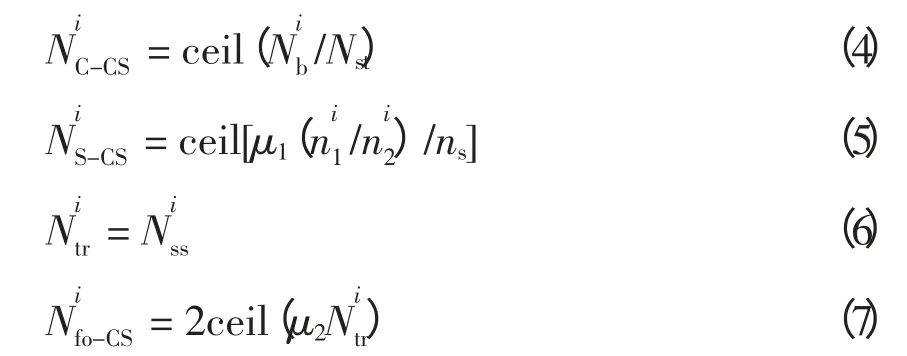
充换电站和换电站的占地面积是影响其建设成本的重要因素，可以参考已建成站的面积，将其折算到每套充电设备和换电设备上的等效面积β1、β2来确定，即

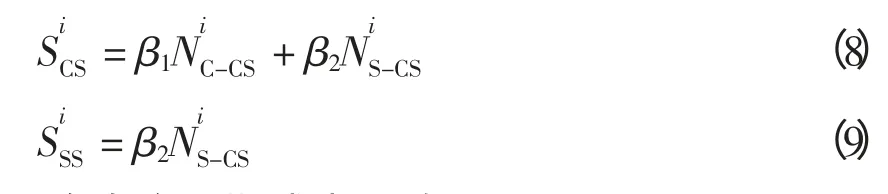
2.3 全寿命周期成本理论

全寿命周期成本是指设备在预期寿命周期内，为研制、生产、使用与保障以及退役处置所支付的所有费用之和[11]。根据国际电工委员会的IEC60300-3-3 标准[12]，设备的LCC 包括购置成本（investment cost）、拥有成本（owership cost）和废弃成本（disposal cost）[13]。

LCC 体现的是资金的时间价值，而电动汽车供能网络的规划建设是一个长时间连续发生费用的过程，应该考虑资金的时间价值；同时也能够将评价规划效果的可靠性、经济性和持续性等指标体现在等效的费用里面，使整个规划模型简单化，只需要优化一个目标，即总费用，从而将多目标优化问题变成了单目标优化问题。故采用LCC 对电动汽车供能网络规划问题进行建模具有重要意义，可以实现经济、社会、环境效益的最大化。LCC模型为

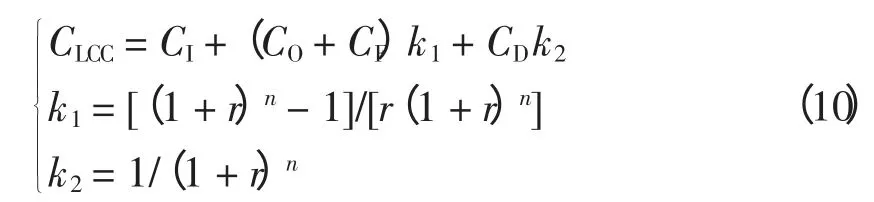
式中：CLCC为全寿命周期成本；CI、CO、CF和CD分别初使成本、年度运维成本、年度故障成本和主要设备的处置成本；k1为年金现值系数，将未来年度的运维和故障费用折算到目前规划阶段；k2为折现系数，将规划期末的处置成本折算到目前规划阶段；n 为寿命周期；r 为社会折现率。

2.4 基于全寿命周期成本的规划模型

供能网络主要包括集中站和换电站，对其成本构成进行解剖，建立规划模型。

（1）初始成本CI主要包括集中型充换电站初期购买电池、充电设备、换电设备、配送车辆、叉车和土地的费用，以及换电站购买换电设备、叉车和土地的费用，即

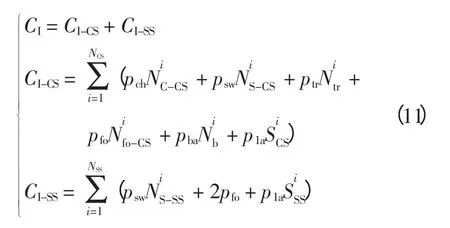
式中：CI-CS和CI-SS分别为充换电站和换电站的初始成本；pch、psw、ptr、pfo和pba分别为充电设备、换电设备、配送车辆、叉车和电池的单价；p1a为城市建设土地综合单价；NCS、NSS分别为整个区域内规划的充换电站和换电站数量。

（2）年度运维成本CO主要包括集中型充换电站的充电损耗费用、配送电池的成本、设备日常维护成本、用户的换电成本和生命周期内更新电池的年度费用，以及换电站的设备维护成本和用户换电成本，即

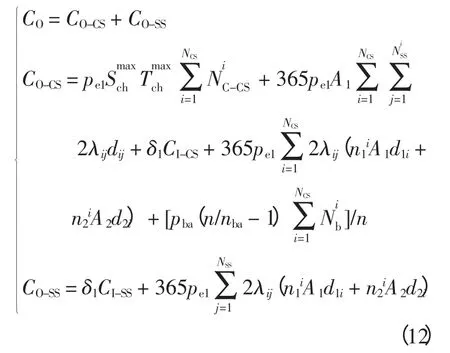
式中：CO-CS和CO-SS分别为充换电站和换电站的年度运维成本；pe1为单位电价分别为充电设备的最大损耗功率和最大负荷利用小时数为集中型充换电站i 服务的换电站数量；dij为换电站j与对应充换电站i 的直线距离；λij为非直线系数[14]，就是将站与站之间或者充换电需求点与站之间的直线距离转换为实际行驶的曲线距离；δ1为设备运维成本折算系数，即通过初始成本来折算设备的维护费用；d1i、d2i（d1j、d2j）分别为集中型充换电站i（换电站j）换电服务区域内2 类车辆的多个换电需求点到站的直线距离之和；nba为电池的使用年限；（n/nba-1）为全寿命周期内整体更新电池的次数。

（3）年度故障成本CF主要包括集中型充换电站的充电设备和换电设备的修复费用、故障造成的卖电损失费用和对用户造成的损失，以及换电站的换电设备的修复费用、卖电损失费用和用户损失费用，其中对用户造成的损失通过产电比方法等效计算[15]，即

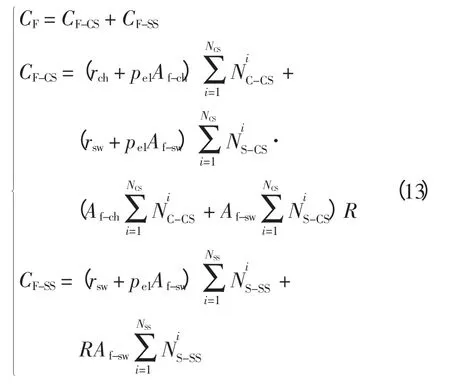
式中：CF-CS和CF-SS分别为充换电站和换电站的年度故障成本；rch、rsw分别为单套充电设备和换电设备的年修复成本；R 为待规划城市的产电比；Af-ch、Af-sw分别为单套充电设备和换电设备因故障造成的卖电损失量，即

式中，Sf、Tf分别为单套充电设备或换电设备的充换电功率和年均故障时间。

（4）主要设备处置成本CD主要包括集中型充换电站和换电站的主要设备报废时处置所需要的费用，以及设备可以回收的部分价值，如大量的电池可以进行梯次利用等，即

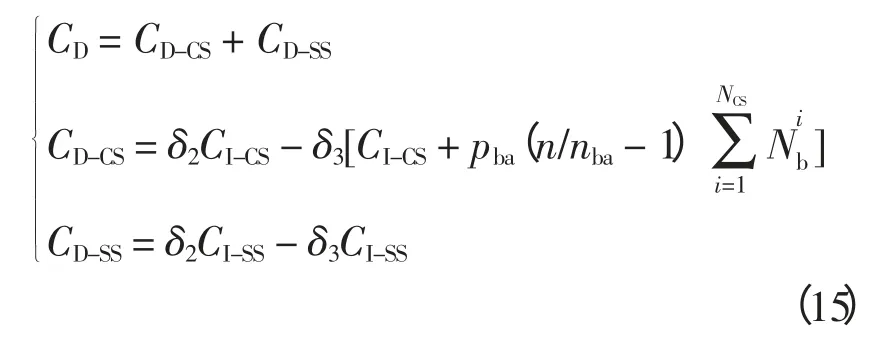
式中：CD-CS和CD-SS分别为充换电站和换电站的处置成本；δ2、δ3分别为设备处置成本折算系数和设备残值折算系数，都可通过初始成本来折算；[pba·为运营过程中更换电池的费用。

根据以上成本建立的规划模型为

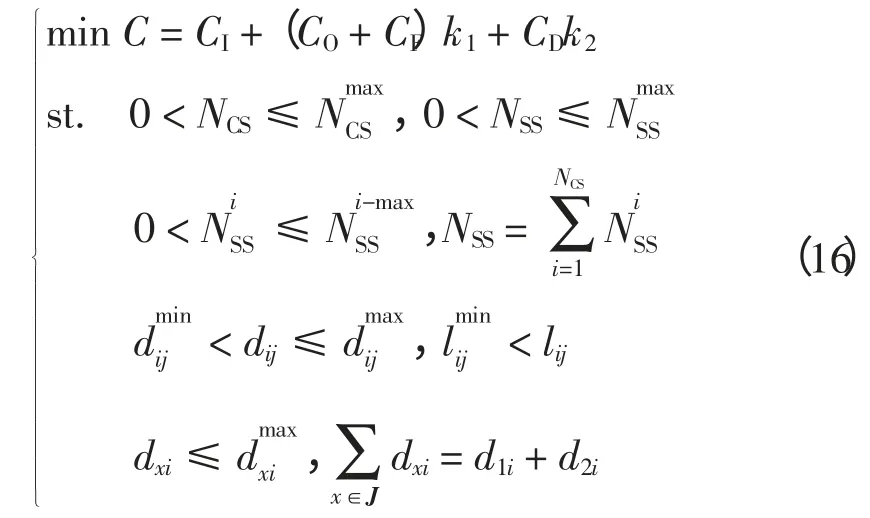
3 模型求解

模型涉及充换电站的服务区域，同时需要求解站址坐标等连续变量，所以结合泰森多边形（简称V 图）和量子差分算法对模型进行求解。

泰森多边形是计算几何的重要分支，在地理、气象、考古中广泛应用[16]。泰森多边形是由区域中已经确定的点向周围扩张形成的凸多边形，因为扩张的速度一样，所以多边形内任何地方到相应点的距离都是最短。由此既可以用来确定集中充换电站为换电站配送电池的区域，又可以确定各站的换电服务区域。

QDEA[17]基于量子进化算法，利用差分进化思想进化部分随机选取的个体，兼具二者较强的局部搜索能力、全局搜索能力和鲁棒性，非常适合需要多次调用算法求解连续空间优化问题的情况。

V 图和QDEA 结合的规划步骤如下。

步骤1 输入规划目标年各换电需求点的大型和小型车辆的保有量及坐标、可用地块的地价以及规划模型的常量参数。

步骤2 通过专家经验，从可以利用的土地中（包括有条件的公交车站），确定集中型充换电站待选站址集G，容量为着重考虑电网接入情况和周围大型公交站情况，尽量将待选站址安排在换电需求较大，且集中的区域。

步骤3 在待选站址集合G 中，选择NCS个站址进行组合，得到x个方案，针对每种方案，以集中型充换电站作为V 图的生长点，产生V 图，得到每个站i 的服务区域。

步骤5 判断NCS是否等于。如果不等，则

NCS=NCS+1，回到步骤3；如果相等，则选出min CNCS，对应的NCS和便是最优的充换电站和换电站座数，对应的坐标便是站址，即得最优规划方案。

4 实例分析

某城市概况：城区规划面积200 km2，城市道路网规划结构为方格与星形组合式，满足建集中型充换电站条件的地块有10 块，其中包含公交站4座。全寿命周期n 取15 a，近期规划到未来5 a，远期展望到未来15 a。已知近远期电动汽车保有量（近期：大型车400 辆，小型车100 辆；远期：大型车2 000 辆，小型车1 400 辆）及大致分布（大型车辆以公交车站分布为主，小型车辆以办公和居住小区分布为主）。电动汽车及充换电设备相关参数见表1，模型的全寿命周期参数见表2，约束条件参数见表3。

利用Matlab 进行建模与求解。根据专家经验得到集中站的10 个待选站址，如图1 所示，再按照步骤3 的方法进行排列组合得到多种方案；每种方案的集中站站址已确定，以其作为V 图的生长点，每个生长点以相同速度向四周扩展直到相遇为止，形成的多个凸多边形就是每个集中站的电池配送（电池充电服务）区域，每个区域中任意点到相应的集中站距离最短，即电池配送成本最小。

表2 模型的全寿命周期参数Tab.2 LCC parameters of the model

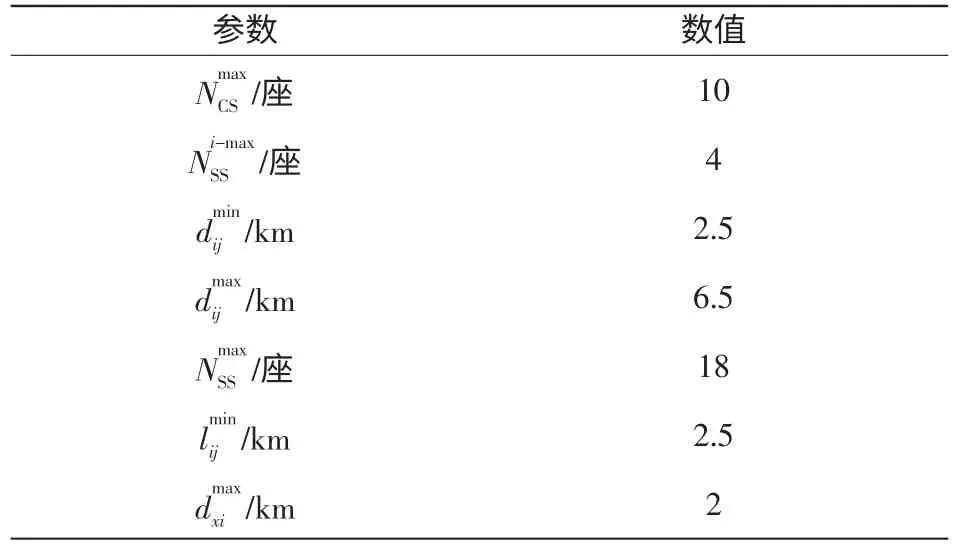
表3 模型的约束条件参数Tab.3 Constraint condition parameters of the model

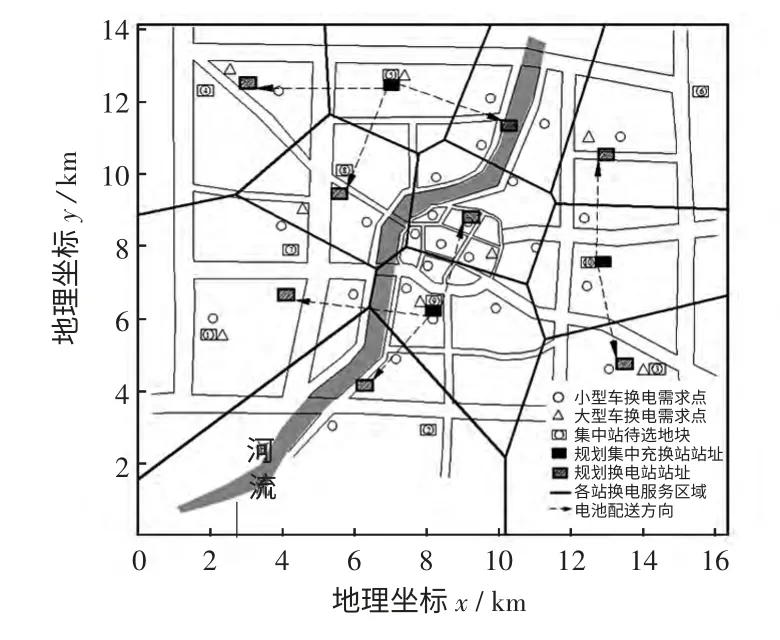
图1 供能网络的最优规划方案Fig.1 Optimal planning program of the battery supply network

在每个集中站服务区域中，初始的换电站数量及对应坐标通过随机产生（满足约束条件），然后通过染色体编码、互补变异和差分进化更新及对应坐标，找到此种集中站分布方案下配送站的最优及对应坐标。最后遍历所有集中站的排列组合方案，找出C 最小的方案即为最优方案。其中QDEA 采用的基本参数：初始旋转角0.4π，进化尺度0.05，连续“求精”次数5，连续“求泛”次数2，实数放缩因子0.5，交叉概率0.4，优秀个体数7，随机选择个体数7，最大运行代数800。在寻优过程中，目标值C 的计算要求明确各个站的换电服务区域以计算各种设备配置数量，同样采用V 图进行划分，只是将集中站和换电站一起作为V 图生长点。

供能网络最优规划方案如图1 所示。从图中可以看到：换电站（10.3，11.3）选址在河流中，应该进行局部调整；换电站（13.5，4.7）、（3.1，12.5）选址靠近集中充换站待选地块3 和4，可以直接选择建在地块3 和4 上，因为这些地块是经过前期论证的。故最优规划方案只是理论上的最优解，并不能完全满足实际工程需求，应该人为进行微调，使其更加符合实际情况。

表4 为3 种主要规划方案的成本对比分析。首先，方案1 的全寿命周期成本C 最小，为最优方案；其次，方案1 的CI大于方案2，即CI最小的方案并不是整个寿命周期的最优方案，CI的最优决策能力是不够的；最后，无论哪种方案的CI都远小于C，只考虑初始建设成本进行工程方案的筛选评价从长远来看是不合理的。图2 是两类成本对集中站数量变化的灵敏度分析。因为单个集中站的成本远大于换电站，所以集中站数量对建设成本控制有着重要的影响。C 对应的曲线斜率明显大于CI，即C 对集中充换站数量变化的灵敏度是大于初始成本CI的，C 能够较好地控制集中站数量（当集中充换电站数量小于3 时，因为不能满足约束条件，从而不能产生规划方案）。故对于电动汽车供能网络这种时间跨度较长的规划问题，采用全寿命周期成本理论是有实际意义的。

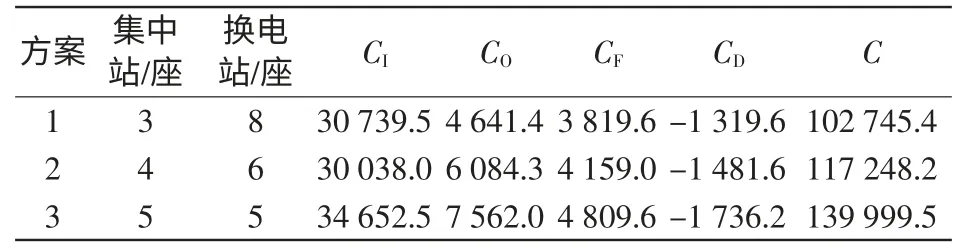
表4 规划方案成本对比Tab.4 Investment comparison of planning programs万元

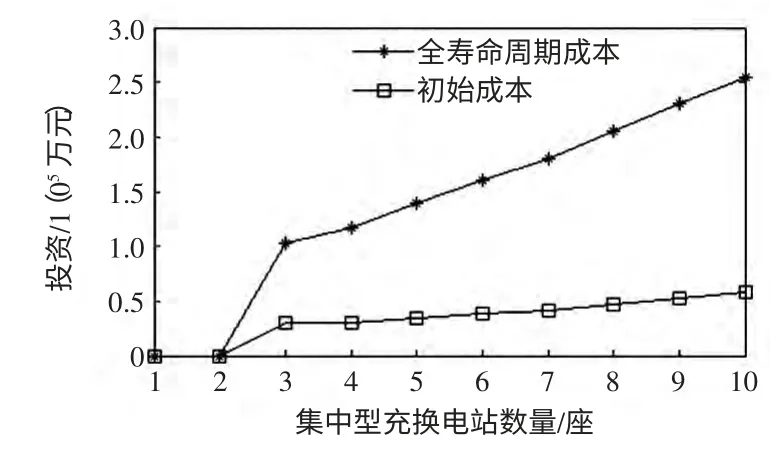
图2 两类成本灵敏度分析Fig.2 Sensitivity analysis of two costs

表5 是对两类站的平均CI的构成进行分析，可以看到集中充换站的CI主要是土地和电池的成本，而换电站的CI主要是换电设备的成本，所以在实际规划中可以着重对这部分成本进行优化，以降低总投资。

在进行未来第2 个五年规划时，已有集中充换站只需增加设备进行扩建，其他新的布点利用本文方法进行规划，以实现供能网络的平滑过渡。

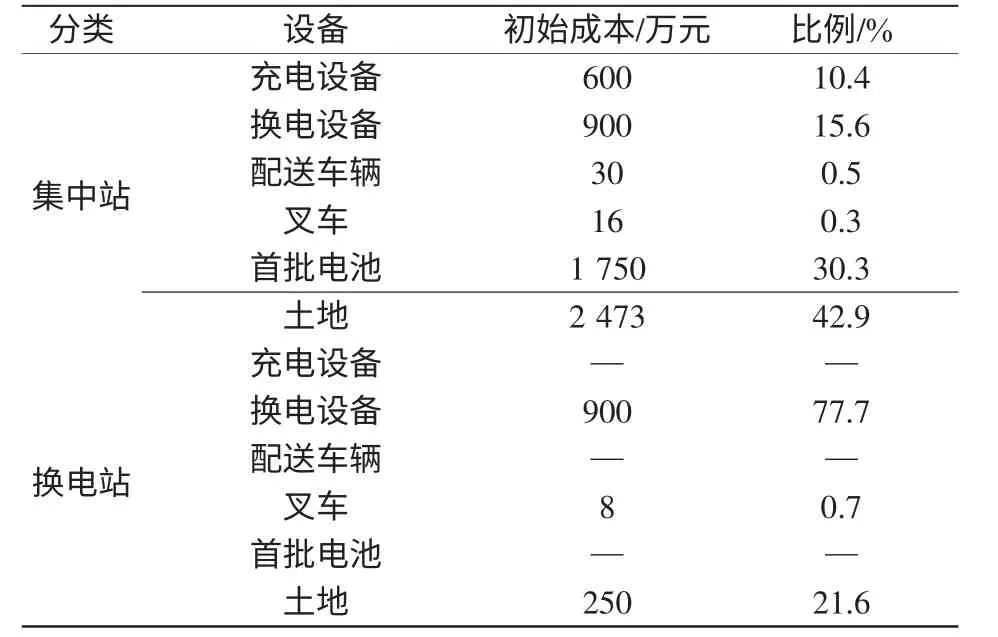
表5 各站平均初始成本的构成Tab.5 Composition of average CI for each station

5 结语

本文重点研究了电动汽车换电网络的规划问题，利用LCC 进行建模，结合数学理论和专家经验对问题进行求解，同时考虑了整个网络从电动汽车低渗透率到高渗透率的平滑过渡，具有一定的实用意义。下一步将着重研究整个换电网络的运行问题，特别是数量庞大的电池如何准确配送，以及兼顾电网和用户的集中充电策略如何与电池配送进行协调调度。

[1]Ozel Fatih Mehmet，Ernst Christian-Simon，Davies Huw C，et al.Development of a battery electric vehicle sector in North-West Europe：challenges and strategies[J]. International Journal of Electric and Hybrid Vehicles，2013，5（1）：1-14.

[2]冯艾，刘继春，吴磊，等（Feng Ai，Liu Jichun，Wu Lei，et al）. 基于前景理论的电动汽车多模式充电行为分析（Analysis on multiple modes charging behavior of electric vehicle based on prospect theory）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（2）：58-64.

[3]陈良亮，张浩，倪峰，等（Chen Liangliang，Zhang Hao，Ni Feng，et al）.电动汽车能源供给设施建设现状与发展探讨（Present situation and development trend for construction of electric vehicle energy supply infrastructure）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（14）：11-17.

[4]张文亮，武斌，李武峰，等（Zhang Wenliang，Wu Bin，Li Wufeng，et al）.我国纯电动汽车的发展方向及能源供给模式的探讨（Discussion on development trend of battery electric vehicles in China and its energy supply mode）[J].电网技术（Power System Technology），2009，33（4）：1-5.

[5]刘自发，张伟，王泽黎（Liu Zifa，Zhang Wei，Wang Zeli）.基于量子粒子群优化算法的城市电动汽车充电站优化布局（Optimal planning of charging station for electric vehicle based on quantum PSO algorithm）[J]. 中国电机工程学报（Proceedings of the CSEE），2012，32（22）：39-45.

[6]刘志鹏，文福拴，薛禹胜，等（Liu Zhipeng，Wen Fushuan，Xue Yusheng，et al）.电动汽车充电站的最优选址和定容（Optimal siting and sizing of electric vehicle charging stations）[J]. 电力系统自动化（Automation of Electric Power Systems），2012，36（3）：54-59.

[7]陈婷，卫志农，吴霜，等（Chen Ting，Wei Zhinong，Wu Shuang，et al）. 考虑电动汽车充电站选址定容的配电网规划（Distribution network planning by considering siting and sizing of electric vehicle charging stations）[J]. 电力系统及其自动化学报（Proceeding of the CSU-EPSA），2013，25（3）：1-7.

[8]李国，张智晟，温令云（Li Guo，Zhang Zhisheng，Wen Lingyun）. 换电模式下电动汽车充换电网络的规划（Planning of battery-switching and vehicle-charging network based on battery switching mode）[J].电力系统保护与控制（Power System Protection and Control），2013，41（20）：93-98.

[9]高赐威，吴茜（Gao Ciwei，Wu Xi）.电动汽车换电模式研究综述（A survey on battery-swapping mode of electric vehicles）[J]. 电 网 技 术（Power System Technology），2013，37（4）：891-898.

[10]Taylor J，Maitra A，Alexander M，et al. Evaluations of plug-in electric vehicle distribution system impacts[C]//IEEE Power and Energy Society General Meeting，Minneapolis，USA：2010.

[11]帅军庆.电力企业资产全寿命周期管理理论、方法及应用[M].北京：中国电力出版社，2010.

[12]International Standard IEC 60300-3-3.International Electrotechnical Commission：Life Cycle Costing[S].

[13]郭峰，文凯，李广福（Guo Feng，Wen Kai，Li Guangfu）.输电线路全寿命周期成本设计（Design of life cycle costs for power transmission line）[J].电力建设（Electric Power Construction），2011，32（2）：29-34.

[14]冯树民，高贺，郭彩香（Feng Shumin，Gao He，Guo Caixiang）.城市道路网结构形式的评价（Evaluation of structural types of urban road network）[J].哈尔滨工业大学学报（Journal of Harbin Institute of Technology），2007，39（10）：1610-1613.

[15]王超，徐政，高鹏，等（Wang Chao，Xu Zheng，Gao Peng，et al）.大电网可靠性评估的指标体系探讨（Reliability index framework for reliability evaluation of bulk power system）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（1）：42-48.

[16]Preparata F P，Shamos M I.计算几何导论[M].庄心谷，译.北京：科学出版社，1990.

[17]张锐，高辉，张涛（Zhang Rui，Gao Hui，Zhang Tao）.求解连续空间优化问题的量子差分混合优化算法（Hybrid optimization algorithm based on quantum and differential evolution for continuous space optimization）[J].系统工程与电子技术（Systems Engineering and Electronics），2012，34（6）：1288-1292.