档案学专业本科学生数学思维和数学素质的调查分析
——以郑州大学档案学专业为例
周拴龙
(郑州大学 信息管理学院,河南 郑州 450001)
档案学专业本科学生数学思维和数学素质的调查分析
——以郑州大学档案学专业为例
周拴龙
(郑州大学 信息管理学院,河南 郑州 450001)
以面向郑州大学档案学专业本科学生的调查问卷为依据,对本专业学生的数学学习观、数学工具应用、数学思维能力进行调查分析,旨在掌握学生数学学习情况以及运用数学思维解决档案学领域专业问题的能力,并给出了建议。
档案学;本科;数学思维;调查分析
一、研究背景与方法
1.研究背景。随着现代信息技术的快速发展,档案学面临着数字化的全面挑战,信息载体从传统纸质记录到计算机长期保存,管理方式从手工操作到计算机网络管理,档案学理论基础和信息技术管理方法正在进行学科融合。这就要求档案学专业本科教育要加深学生工科思维和能力的培养,而数学学习无疑是达到这个目的的重要途径。本调查问卷以郑州大学档案学专业大一到大四在校学生为调查对象,旨在掌握学生数学学习情况以及运用数学思维解决档案学领域专业问题的能力。
2.研究方法。选取郑州大学档案学专业,以年级取样发放问卷120份,回收发放问卷120份,回收率为100%。有效问卷为103份,有效率为85.8%,其中一年级29份,二年级30份,三年级25份,四年级19份。
《大学本科档案学专业学生数学思维和能力培养的问卷调查表》从理论和实践两个角度出发,确立了数学学习观、数学工具应用、数学思维能力及应用三个一级方向,共设计14个基本问题,从不同角度了解档案学学生数学思维和素养在学习中的应用能力。表1给出了具体方向及题项设计。

表1 调查问卷题项设计
二、数学学习观情况调查和分析
郑州大学档案学专业本科阶段开设的数学课有微积分、线性代数、概率论,其中少数学生选修了离散数学和数理统计。在数学课的学习过程中,51.85%的学生认为所有的数学课很难,29.63%的学生认为某一门或两门难,只有1.85%的学生认为数学课很容易;就主观爱好而言,9.26%的学生很喜欢数学课,29.63%的学生很不喜欢数学课,51.85%的学生对数学课介于两者之间。从学生对数学课的认知角度而言,42.59%的学生认为数学课对于自己所学专业非常没有必要,55.55%的学生认为档案学专业对数学有一些需求,其中62.96%的学生认为归纳法和统计方法是本专业需要的数学方法,其他方法的重要度依次为推理、逻辑、类比、抽象、演绎等,本专业学生对各种数学方法的主观认知如图1显示。
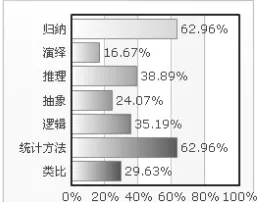
图1 档案学专业学生对各种数学方法重要度的主观认知
从以上的数据可以看出本科阶段档案学专业学生对数学课的重视程度不足,这是因为,从学科的主干课程表层上看,数学课仅仅是作为一门公修课来学习,教师一般是来自于教授公共课的数学系,这样就将数学和具体学科分离开,学生无法理解将其作为工具解决学科中的实际问题。
三、数学工具的学习情况调查和分析
SPSS(Statistical Product and Service Solutions,统计产品与服务解决方案)是社会学科常用的一个统计工具,它能够帮助档案管理人员将档案工作的真实情况通过准确的统计数字反映出来。调查显示只有18.52%的学生接触过SPSS工具,其中70.00%是通过上课时老师提及,其余的30.00%是通过网络或者课外科研活动接触到,同时在接触过SPSS的学生中40.00%的学生能够使用SPSS解决一些基本的档案统计问题。
数学工具是数学理论和学科实践联系的纽带,能够使学生直观地将数学模型应用于学科实践,如果学科院系能够开设专门的课程学习SPSS或类似的工具软件,那么学生不仅能够掌握档案统计工具的使用,更重要的是从学习观层次提高对数学的重视程度。
同时,SPSS软件还具有强大的数据挖掘功能,这就给目前重藏轻用的档案业界提供了一个具有实际应用价值的方向。例如,挖掘档案馆到馆的用户记录,能够得到档案馆不同行为用户分类、同类用户之间的相互协作关系等;挖掘馆藏档案的使用记录,能够得到档案被使用的时间性、地域性等规律。这些数据能够为档案馆优化管理提供有力而且客观的数据支持。
四、数学思维能力及应用调查和分析
在调查表中涉及到的数学思维包括:维度、分类、图、运筹等,在档案学专业的学习和工作中处处体现了这些数学思维的智慧。
1.维度。在物理学中,维度是指独立的时空坐标数目[1],我们所处的空间有3个空间维度和1个时间维度,这就是爱因斯坦所称的四维空间。但在数学中,维度指的是问题中独立参数的数目,这样就从本质上将空间概念扩展到n维空间,不同参数取值表示高维空间中不同的点,对应于高维空间中的独立物体。数学中的高维空间能够应用于更多的社会科学领域,例如,档案描述编码格式EAD,同一个层次中的每一个元数据都是EAD空间中的一个维度。在调查中,有55.56%的学生不能理解高维物体,这显然表明,大多数学生概念中的高维空间仅仅是物理学中的空间概念,而未能理解数学上空间维度的本质,线性代数就是解决高维空间问题最直接的理论基础。例如,档案统计学中的统计指标对应于一个n维向量,n表示具体指标的数量,有了这样的数学模型就可以借助数学方法得到定量的统计结果。
2.分类。分类学是分门别类的科学。广义分类学包括许多细分学科,例如,信息分类学、数值分类学等,狭义分类学特指生命分类学。在调查中,只有7.41%的学生在日常的生活学习中不会分类。由于分类法是档案学专业重要的一门基础课,因此有2.50%的学生认为分类并不属于数学的范畴,根据分类学的定义并不无道理。但是在现代网络环境下,我们通常借助于计算机算法将海量的数字资源进行自动分类,而这些自动分类算法所依据的数学基础便是集合论中的一个概念——划分。将具有相同或相似特征的资源分为一类,在分类的过程中可以依照已经存在的知识,这叫做分类,如果在分类的过程中经过算法计算资源的相似程度而得到的分类叫做聚类,也称作无先验知识的聚类。
3.图论。图论是数学的一个分支,它以图为研究对象,研究顶点和边组成的图形的数学理论和方法。图论中的图是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用顶点代表事物,用连接两顶点的边表示相应两个事物间具有这种关系。在调查中,有44.44%的同学使用过画图的方法帮助自己理解或记忆某个问题,例如,确定两地之间的最短路程、归纳知识点及其联系等问题。在档案学专业领域,电子文件从生成到归档的处理流程借助于一种特殊的图——Petri网可以建立起清晰的模型,这是电子文件管理系统流畅运行的基础,事实上,大多数的电子政务系统也是建立在Petri网的公文流转模型基础之上的。除此以外,档案分类的树形结构图也具有图论中树的普遍特征,树根、分枝、树叶以及层次等概念也适用于分类树。
4.运筹。运筹学是应用数学和形式科学的跨领域研究,利用统计学、数学模型和算法等方法,去寻找复杂问题中的最佳或近似最佳的解答。运筹学的研究特点是将许多具有典型性的问题,抽象成具有共性的数学模型,对模型求解后再对解进行切合实际的解释,然后把结果用于这类问题。在调查中,25.93%的学生在日常生活和学习中能够井井有条地同时处理多件事,62.96%的学生在需要去多个地方时能够根据不同需求制定最优的方案。很多学生在制订最优方案时并没有完全意识到这是运筹学的具体应用,原因在于在面临类似简单问题时我们并没有显式地将问题抽象成数学模型的过程,但是在处理复杂问题时运筹的过程就尤为重要。例如在档案学领域,档案载体由纸制环境迁移到电子环境下,管理流程也从线性串行结构转变为各个环节的交叉并行结构[2],那么我们可以以各个环节的开始时间为依据优化其管理流程,利用运筹学的组合优化理论解决并行问题。
此外,档案学中还有许多重要理论也透射着数学思维的光芒。例如,电子文件前端控制理论有效预防威胁电子文件真实与完整的风险,保证了电子文件归档质量,而这一思想恰恰体现了如何对一个动态系统的不确定性加以控制的数学本质。
因此,如何帮助档案学专业学生建立起适当的数学思维并能够利用数学工具解决本学科的实际问题就显得尤为重要。
五、建议
首先,学生应学好各门数学课程,提高自身数学素质和数学综合应用能力,培养创新精神。同时,加强档案学数学教师与专业教师横向联合,互相弥补知识上的欠缺,开展跨学科的多方位研究,拓宽档案学学术研究空间和专业教育平台。其次,为了更好地适应学科融合的趋势,档案学专业可以适当引进其他相关专业的高学历人才,如图书馆学、情报学、计算机、公共管理学等专业背景的教师,从而进一步满足专业发展和教学的需要。
[1]百度百科[EB/OL].2013-08-10. http://baike.baidu.com/link?url=5oXPUhGkwgGLR 2A5c_G-tk73rNatURn8qlfi1QKu4KoiqXUmG9qyVLSnw yuJ1mnyq.
[2]郭亚军.电子文件非线性管理特征与实施研究[J].北京档案,2012,(7):17-19.
G645
A
1674-9324(2014)45-0073-03
河南省教育厅自然科学项目:病历档案数字化加工与应用系统的设计与实现(2011A520042)
周拴龙(1964-),男,河南辉县人,郑州大学信息管理学院副教授,研究方向:数据库全文检索、电子病历档案管理、复杂系统理论等。
——《魂系历史主义——西方档案学支柱理论发展研究》述评

