电压模式控制单级反激变换器的快时标分岔研究
王磊
(韩山师范学院物理与电子工程系,广东潮州 521041)
电压模式控制单级反激变换器的快时标分岔研究
王磊
(韩山师范学院物理与电子工程系,广东潮州 521041)
以电压模式控制单级反激变换器为研究对象,在简化的离散时间模型基础上,运用非线性动力学对其稳定性问题进行了探讨,基于特征值的稳定性分析和仿真结果能够较好的吻合,并与相同运行点的直流变换器的仿真进行了比较.
单级反激变换器;电压控制;分岔;快时标
1 引言
近年来,开关电源中的非线性现象受到越来越多的电力电子领域专家的关注[1-4].批量的开关电源产品中有一些在正常运行中会突然崩溃,或出现不明的电磁干扰,这种现象主要原因是电源构成器件的非线性特性及开关的高速切换、敏感参数的细微差异导致分岔并进入混沌状态.通过研究开关电源中的非线性动力学规律,将会加深对开关电源系统的认识,有助于设计出更可靠的开关电源.
反激变换器本质上是Buck/Boost变换器的隔离版本[5-6],由于其结构简单、控制方便、性价比高,被广泛应用在150 W以下的功率变换场合.由于功率变压器的引入,在结构上反激变换器与基本的变换器有了本质的区别,目前对其非线性动力学特性还缺乏深入系统的研究.
本文对电压模式控制的单级反激变换器建立了简化的离散时间模型,并采用基于特征值的稳定性分析方法对快时标分岔现象进行了分析,然后得出了两个关键参数的稳定域.分析和仿真吻合得比较好,并与对应的直流变换器的仿真进行了比较,对基于特征值的分析方法在对交流输入变换器的稳定性分析误差原因进行了深入的探讨.
2 电压模式控制单级反激变换器的运行原理
电压模式控制单级反激变换器的拓扑结构见图1(a),仅包含比例环节的单电压反馈环.电压环的核心是运放和PWM比较器.输出电压的采样信号接入运放的负端,电压环的基准Vref接入运放的正端.两者的误差通过比例放大得到控制电压Vco,并接入PWM比较器正端,与接在负端的锯齿波Vsaw比较形成PWM脉冲控制开关Q1.一个工作周期开始时,锯齿波下降至较低电位,比较器输出高电位,Q1导通;当锯齿波的线性上升部分与Vco相遇,比较器输出低电位,Q1关断.图1(b)是电压环控制电压的波形和锯齿波相比较,产生了与Vco幅度成正比关系的开关驱动脉冲.

图 1 电压模式控制单级反激变换器及典型控制波形
仿真中,为了与实际更接近,最大占空比限制在0.9.控制信号饱和(占空时间超过周期)会引起边界碰撞分岔等更复杂的不稳定情况,本文不予考虑.
为了实现功率因数校正,单电压环控制的单级反激变换器必须运行在电感电流不连续模式.变换器也可能以很复杂的方式在两种模式间跳变.正常的运行指稳定的连续模式周期-1运行.不稳定指输出无法稳定的运行状态,分岔指从一种模式运行变为另一种.
反激变换器的变压器实质是个耦合电感,一次侧的电流是不可能连续的,因为开关关断之后,一次侧的电流必然为零,但同时在二次侧产生感应电流.所以对于反激变换器来说,电流连续指的是变压器的两个绕组合成安匝在一个开关周期一直大于零,而电流断续指的是合成安匝在开关关断期间有一段时间为零.图2给出了DCM运行时反激变换器原副边电流及安匝和 jps=ip+is*Ns/Np的波形,其中一个周期Ts里的三个模态,分别对应ts和td两个时间点.
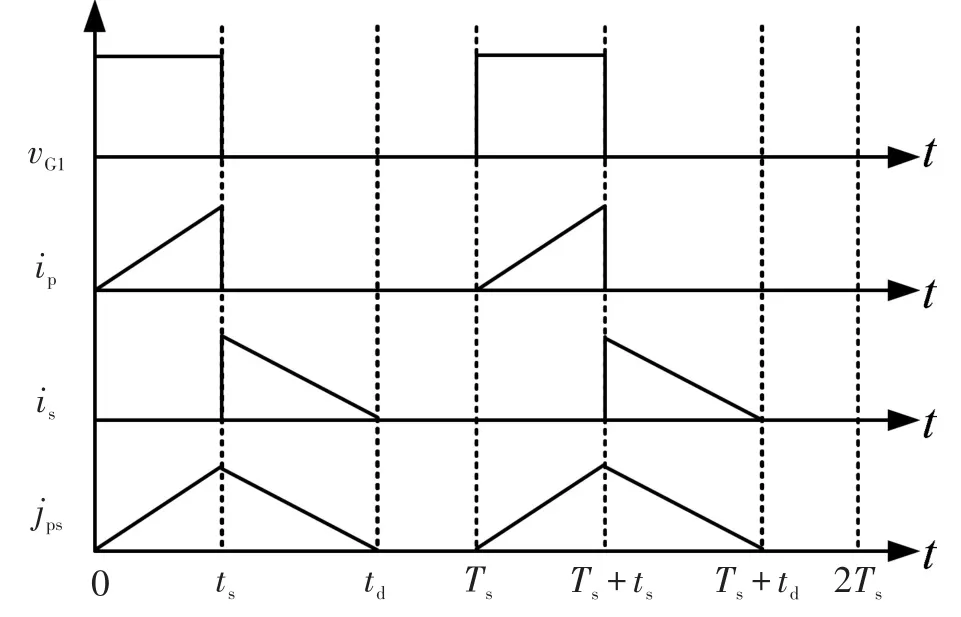
图 2 断续模式下变压器原、副边电流波形和对应的安匝和波形
不连续模式下反激变换器每个周期有三个模态:
开关模态1:当Q1导通时,变压器原边Lp承受交流输入e(t) =Vm*sin(wt),原边电流ip从零开始线性上升;D1承受反压关断,输出电压由电容维持,状态方程为

开关模态2:当Q1关断时,ip按照安匝守恒的关系转移到副边电流is,即为Np*ip=Ns*is,且Lp/Ls=Np
2/Ns2,ip变为零;副边D1导通,is给输出电容和负载供电,直至is为零,状态方程为

开关模态3:当变换器处在不连续模式时才会出现模态3,此时原副边电流均为零,输出电压由电容维持,状态方程为

状态变量x选为原边电感电流ip、输出电容电压vc.反激变换器在DCM模式下的状态方程可以表示为

电压控制下反激变换器的状态矩阵Ai、Bi分别为
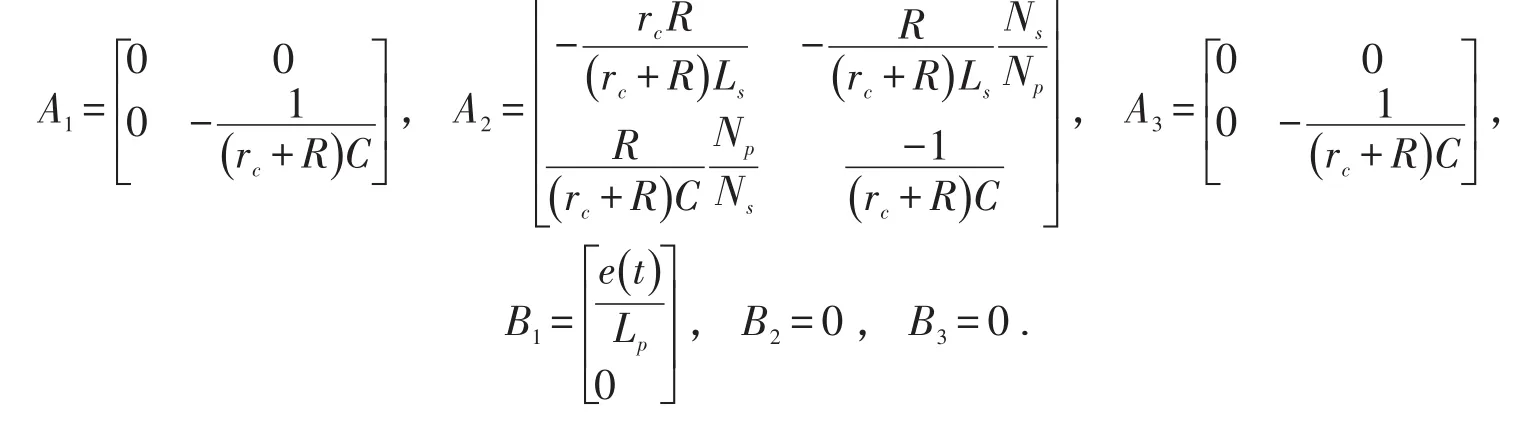
3 电压模式控制单级反激变换器的简化离散模型
一般对变换器的分析可基于3种模型:连续时间模型,离散时间模型,及连续、离散时间模型的组合.基于状态空间平均的连续时间模型的小信号分析方法不能研究快时标动态,因为它对高频特性进行了平均;精确的离散时间建模方法可以捕捉到快、慢时标的分岔,但其表达式较为复杂,无法直观看出各个参量对变换器运行特性的影响.截去状态转移矩阵的展开级数高阶项,即得到简化的离散时间模型[7-8],可以看做对离散时间模型进行了平均.由此可以得到平衡点和特征多项式的解析式,减少了运算量,而且可以解释系统参数互相作用产生的不稳定.
对变换器建模要得到的离散迭代映射应具有下面的形式

其中下标n代表第n周期开始时的值,即xn=x(n T).
状态方程(4)是电流控制反激变换器的精确离散模型,属于超越方程,没有解析解,因此无法写成(5)的形式,只能用来迭代计算以得到数值解.求解(4)式得到:

其中ts是开关导通的占空时间,Ts为工作周期.指数矩阵展开是无穷级数:为得到简化的离散时间模型,采用线性纹波假设,若dn代表第n个开关周期的占空比,则有ts=dn*Ts,代入(4)式并对其解的展开式中所有含有Ts的二次及高次的项加以忽略,(6)式可简化为:

由于变换器工作于DCM,ip在起始和结尾都为零,且在第三模态保持为零,因此从(7)式可以得到:

定义开关函数:


很明显,式(8)、(10)两式共同定义了一个基于线性纹波假设的大信号离散时间平均模型.依据电感的伏秒平衡原则可知ts和td的关系:

4 电压模式控制单级反激变换器的分岔分析
基于上面的简化离散模型,可以对电压控制的单级反激变换器的稳定特性进行进一步分析.常规的分析方法有雅可比矩阵法、单值矩阵法、最大李雅普诺夫指数和庞加莱截面法.由于对离散模型进行了简化,可以按照雅可比矩阵法的步骤,分析其特征值.
一定输入功率Pin下单级反激变换器的稳态占空比为:

在(8)式中令vc()n+1=vcn=Vcq,同时将Dq代入,即可得到Vcq.这样由Dq和Vcq定义了变换器的平衡点.将(10)代入(8)并对vcn求导,即可得到特征乘子的表达式.为了保证系统的稳定,平衡点附近的特征乘子必须满足:

其中依据不动点处特征值所处的位置,用下面的判据判定系统的分岔行为:
1)所有特征值都在单位圆内预示着系统稳定工作;
2)当一对共轭特征值在单位圆外而其他特征值都在单位圆内,系统为慢时标分岔;
3)当一负实数特征值在单位圆外而其他特征值都在单位圆内,系统为快时标分岔;
4)当一对共轭特征值和一负实数特征值同时在单位圆外,系统为共存快-慢时标分岔;
5)当运行的控制量饱和及有特征值在单位圆外时,会出现复杂的边界碰撞分岔.
下面运用上述关系式对一个具体的反激变换器进行分析.变换器的主要参数见表1,为了研究稳定参数边界,负载电阻和比例k都在一个范围内取值.

表1 反激变换器的电路参数
当Ro=10Ω,k=0.18时,得出图3,其中(a)图是反激变换器特征值随着vin在半周期的改变(见(b)图)而变动的轨迹.随着vin增大,λ逐渐减小,在vin峰值处取到最小值.依照上面的判据可知,系统可能出现快时标分岔.其中λ=-1的临界点出现在vin为141 V处.
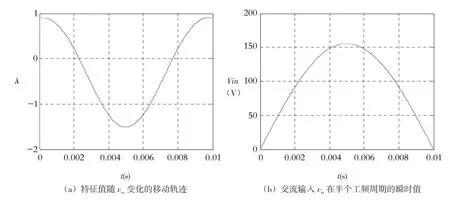
图 3 反激变换器特征值随vin变化的移动轨迹
由图3可知,λ在vin峰值处取到最小值,因此求取参数边界时,只需要看vin峰值处的特征值即可.下面图4(a)、(b)分别给出负载电阻Ro在3~15 Ω及比例k在0.1~0.2之间变动时,λ最小值的轨迹.(a)图得到临界电阻Ro4.1 Ω,(b)图得到临界比例0.14.

图 4 电压模式控制单级反激变换器在负载电阻和比例系数波动时λ最小值的轨迹
5 电压模式控制单级反激变换器的仿真
为了验证上面稳定性分析的结果,用表1同样的参数,采用精确的离散模型对反激变换器进行仿真.下面图5(a)是交流输入反激变换器的输入电流仿真波形,作为对比,图5(b)是直流输入电压为156 V的反激变换器的输入电流仿真波形,从图5(b)放大的输入电流波形可见,快时标分岔时相邻开关周期的输入电流波形有一定的跳动.
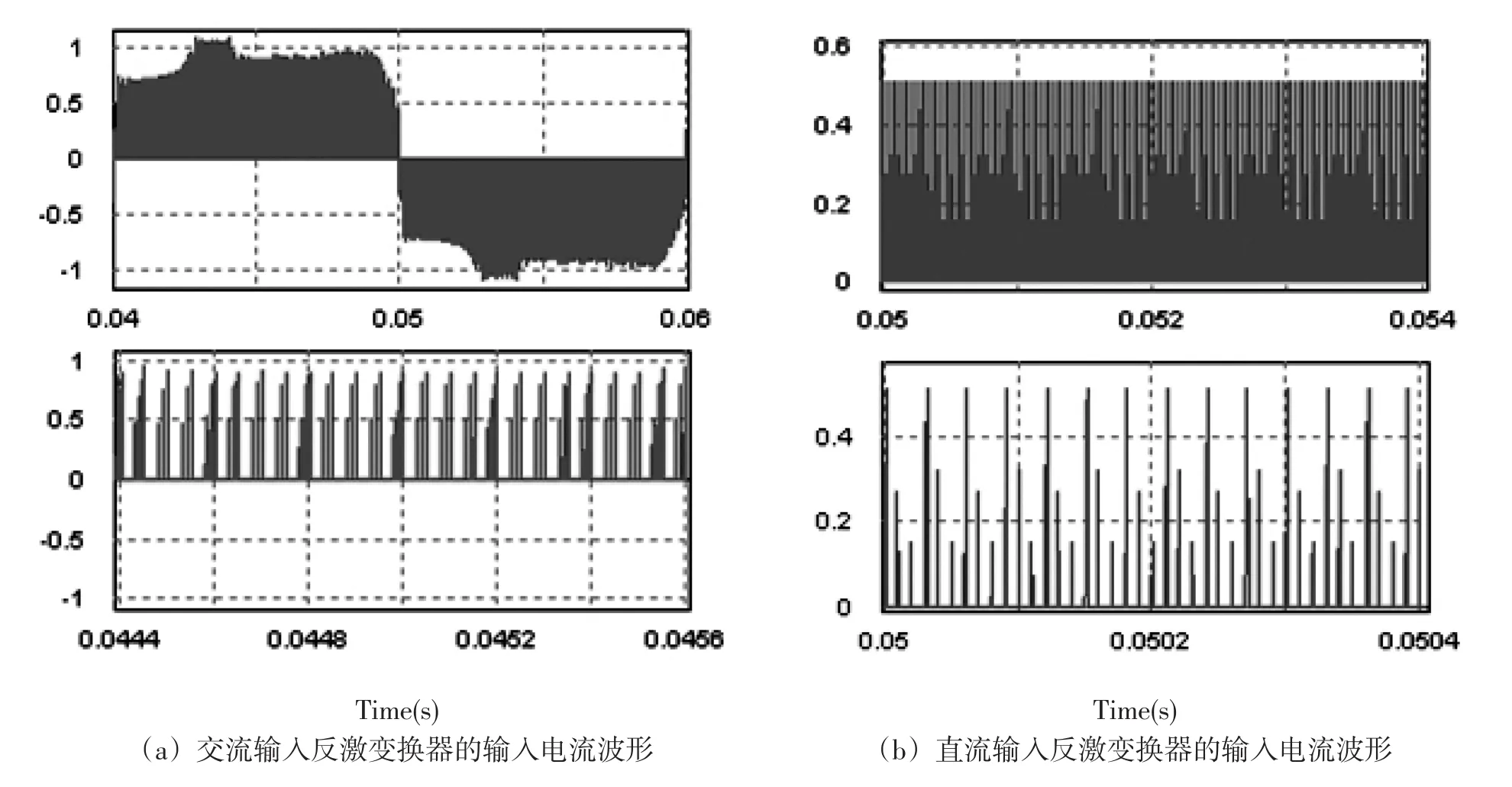
图 5 电压模式控制反激变换器的输入电流波形(Ro=10Ω,k=0.18)
通过多次运行仿真得到的结果与分析结果的对比发现,分析数据和仿真数据划定的区域分界是比较接近的.存在的一些差异有两方面的原因.首先是分析方法的差异,由于分析方法不能体现仿真的一些设定.在特征值的分析中无法体现占空比最大为0.9的限制,而且分析模型取了线性近似.因为接近稳定边界系统的控制特性会比较差,设计参考应以分析数据的稳定区分界为准.其次是变换器本身运行情况和分析方法的假定有差异.因为交流输入一直在随时间而变化,电路并未真正进入稳态,交流输入过零时会积累较大的误差,因此主要是初态以及是否进入稳态的差异.特征值分析法对直流变换器稳定工作点的分析较为准确,交流输入没有真正意义上的平衡点,因此分析会出现偏差.初态的差异会体现为vin在峰值两侧相同的瞬时输入电压下系统特征值不同.
6 结论
本文对电压控制的单级反激变换器的快时标分岔做了研究,采用基于特征值和平均离散模型进行了分析和仿真验证,两者能够较好地吻合.本文的结果对电压控制的反激变换器的参数设计有一定的参考价值,同时对一般变换器基于交流输入和直流输入的稳定性的不同特征进行了分析对比,分析的结果具有一般性的意义.
[1]谢帆.DC-DC开关变换器分段光滑系统边界碰撞和分岔研究[D].广州:广州大学,2011.
[2]戴栋,张波,李胜男,等.单级PFC变换器中的Hopf分岔[J].电工技术学报,2008(11):65-71.
[3]罗晓曙.DC-DC变换器的非线性动力学行为与混沌控制[M].北京:科学出版社,2012:341.
[4]XIAOQUN W,TSE C K,DRANGA O,et a1.Fast-scale instability of single-stage power-factor-correction power supplies[J]. IEEE Transactions on Circuits and Systems I,2006(53):204-213.
[5]毛照中.反激开关电源的混沌现象与混沌控制的研究[D].哈尔滨:哈尔滨理工大学,2010.
[6]高振江.开关电源中的混沌现象的研究及反激式电源的研制[D].合肥:安徽理工大学,2013.
[7]YANFENG C,TSE C K,SHUI-SHENG QIU,et a1,Coexisting Fast-Scale and Slow-Scale Instability in Current-Mode Con⁃trolled DC/DC Converters:Analysis,Simulation and Experimental Results[J].IEEE Transactions on Circuits and Systems I, 2008(55),:3335-3348.
[8]PAVLJASEVIC S,MAKSIMOVIC D.Using a discrete-time model for large-signal analysis of a current-programmed boost converter[C].IEEE PESC.,1991:715-721.
A Study on Fast-scale Instability in Voltage Controlled Single-stage Flyback Converter
WANG Lei
(Department of Physics and Electronic Engineering,Hanshan Normal University,Chaozhou,Guangdong,521041)
The closed-loop stability characteristics of single-stage flyback converter under voltage con⁃trol is investigated based on the simplified discrete-time model using nonlinear dynamics method.The stability analysis based on the eigen value of Jacobin matrix is in relatively good agreement with the simulation results. And the comparison with the corresponding DC converter is provided.
flyback converter;voltage-mode control;bifurcation;fast-scale instability
TM463
A
1007-6883(2014)06-0036-07
责任编辑 朱本华
2014-11-06
王磊(1978-),男,湖南娄底人,韩山师范学院物理与电子工程系讲师.

