Fatigue Crack Initiation Potential from Defects in Terms of Local Stress Analysis

ZHU Mingliang and XUAN Fuzhen

1 Key Laboratory of Pressure Systems and Safety, Ministry of Education, Shanghai 200237, China

2 School of Mechanical and Power Engineering, East China University of Science and Technology,Shanghai 200237, China

1 Introduction

Generally, fatigue damage involves three stages:micro-crack nucleation, small crack growth, and macro-crack propagation. It has been realized that the fraction of the crack initiation or growth life depends strongly on the applied amplitude. Particularly, for small cyclic loadings in components operating in ultra-long life(fatigue life > 107cycles) regime, almost more than 90% of fatigue life is consumed in the stage of crack nucleation[1]. The failure life beyond 107cycles is often named very high cycle fatigue(VHCF). In the VHCF regime, to predict the fatigue life in the primary stage, one fundamental aspect is the dependence of crack formation on cyclic load levels, i.e., higher cyclic loading amplitudes often lead to the surface crack initiation while subsurface crack nucleation occurs at lower loads[2–3]. As a result, it is reported that subsurface inclusions[4–5], pores[6–7]and even interior microstructure heterogeneities[8]can initiate cracks under fatigue loadings. Therefore, the understanding of subsurface crack initiation mechanism in the VHCF regime had been a critical issue for the safety and reliability of long-term service components in recent years.

The intrinsic aspect of subsurface failure is related to defects, such as the inclusion and pore. ZHANG, et al[9],and MUGHRABI[10]related the VHCF behavior to the shape, size, and thus distribution of non-metallic inclusions in high strength materials through experimental observation.By 3-D finite element simulation, FARIDA, et al[11],discussed the influence of geometrical parameters of the pores on the strain localization and crack initiation behavior.One of the important issue for the defect location is how to define and differentiate the surface and subsurface defects.As a result, MAYER, et al[12], proposed a definition for surface and interior porosities based on their distance to specimen surface. Another critical issue is how to model the crack initiation transition behavior from surface to subsurface. MUGHRABI[10]suggested that there was a competition between surface and subsurface crack initiation.CHANDRAN, et al[13], also argued it was the competitive phenomena of surface and interior inclusions that was responsible for the transition of crack initiation from surface to interior. Therefore, the distribution of defects should be considered in both experimental and simulation processes. MURAKAMI, et al[4,14], introduced a location factor to evaluate the transition of fatigue crack initiation from surface and subsurface defects. In order to model the crack initiation potency for pores, BORBÉLY, et al[15],considered the depth factor of pore in the simulation process and obtained the most probable case for subsurface crack formation. Whereas GAO, et al[16], demonstrated the pores which were both large and near to the specimen surface induced much higher stress concentration. Recent work by XU, et al[17], took the ratio of pore location to size as a correlating parameter, and found that the maximum stress concentration occurred where the pore was just buried beneath the surface. FENG and XUAN[18]reported the cyclic hardening effect on crack initiation from pores,and discussed crack nucleation in the case of multi-inclusions. However, all these investigations are mainly focused on pores and their distribution, which is insufficient to provide detailed information for the subsurface crack initiation transition behavior. An importrant reason is that the integrity of the inclusions and their cohesive behavior with matrix should be considered[19].Moreover, the roles of defect types and properties in subsurface crack initiation, i.e., pores, hard or soft inclusions(relative to the matrix), are yet to be comprehensively evaluated.

Another aspect of subsurface failure is the influence of extrinsic factors, such as high temperature and residual stress. Numerical simulations by PRZYBYLA[20]and ZHU,et al[21]presented a promotion of subsurface initiation in the case of some thickness of oxide layer on specimen surface.Surface compressive residual stress, which is often introduced to improve fatigue durability, contributes to the crack initiation transition from specimen surface to subsurface[22]. Unfortunately, a quantitative evaluation of the residual stress influence on the transition of crack initiation mode has not been documented in literatures.

In the present work, finite element simulations were performed to investigate the mechanisms of subsurface crack initiation in the VHCF regime. Effects of several factors such as defect types, properties, location, and residual stress(RS) on the crack initiation potency were going to be addressed.

2 Finite Element Modeling

Commercial finite element software ABAQUS was used to simulate the stress localization around defects based on standard analysis with reduced integration method. Finite element models(FEM) were established in terms of the hourglass shaped fatigue specimen shown in Fig. 1(a). All the computations were conducted by assuming the isotropic linear elastic non-metallic inclusion embedded in an elasto-plastic matrix. Here, the material matrix was modeled as a low strength steel with an elastic modulus Emof 232 GPa, and a Poisson’s ratio ν of 0.3. Elastic modulus of inclusion Eincwas treated as a variable, and thus leading to various ratios of Einc/Em. The elasto-plastic parameters of the matrix was obtained from tensile test at room temperature, and was reported in Ref. [21]. The inclusions or pores in the models were always circular while elliptical defects were employed to investigate the influence of defect shape on crack initiation potential.

As shown in Fig. 1(b), the defect was assumed to locate at the specimen’s smallest cross section. The depth of the inclusion had been denoted using dinc(here, dinc≥ 0) which was defined as the distance from the center of inclusion to the specimen surface. In terms of the symmetry of specimen, the model was reduced to one quarter of the specimen shape(Fig. 1(a)). The four node bilinear axisymmetric quadrilateral elements with reduced integration(CAX4R) were used as the element type for meshing. The total number of elements were at least 3000.Generally, the results of numerical calculation were strongly related to the quality and density of the mesh around the pores or inclusions. In this paper, a series of element size was chosen at first, and then by reducing the element size gradually, an optimized element size was obtained finally when the stress around inclusion was almost stable. More elements with the same element size were used to mesh the inclusion and its surrounded matrix.The details of the model including boundary conditions are presented in Fig. 1(c). Tensile static load was used and all the inclusions were assumed to be bonded well with the matrix. This simplicity was based on the assertion that the location of plastic strain concentration under cyclic loading would be the same as those of stress concentration in the case of static loading[17]. Therefore, crack nucleation potential should not be influenced by external load mode(cyclic or static).

In addition, three-dimensional finite element models based on one-half of the specimen shape were established to investigate the residual stress effect. As depicted in Fig.1(d), the model was meshed using eight-node brick element with reduced integration(C3D8R). The total element numbers were at least 80 000 and dependent on the location of non-metallic inclusions. The residual stress was introduced by imposing a moment along z axis (Mz) at the center of the specimen’s largest cross section and then unloaded. The distribution of RS changed with the value of Mz. Then a static load was imposed to obtain the stress distribution in the specimen containing residual stress. Such large number of elements and complex loading scheme consumed a large amount of computational time and proposed a demanding capability for computers. Here, the inclusions were assumed as spherical shape with a diameter of 140 μm. Both soft and hard inclusions were considered,i.e., Einc/Em= 0.5 and 2.

Fig. 1. 2-D and 3-D Finite element modeling

3 Results and Discussion

3.1 Effect of defect properties

Fig. 2 shows the stress concentration factor Ktas a function of dinc/d around inclusions and pores. Ktdenotes the ratio of the largest Mises stress with and without defects.dinc/d is the ratio of defect depth to diameter. In the case of Einc/Em≤ 1, these inclusions are relatively softer than matrix, and thus called soft inclusions. It is observed that the overall Ktis the highest at pores(Einc/Emcan be seen as zero) and then gradually reduced with increasing of Einc.Therefore, cracks are much easily initiated from defects since Ktcorresponding to Einc/Em= 1(the matrix is free from micro-defect) is the lowest one. It is also worth noting that any soft inclusions that are located at specimen subsurface have higher Kt. This indicates the higher probability of crack initiation from subsurface defects.

With Einccontinues increasing, e.g., Einc/Emis above one,this denotes a relatively harder inclusion than the matrix,and the inclusions are referred to as hard inclusions. It is observed in Fig. 2 that the larger Eincof hard inclusions, the higher values of Kt. Interestingly, surface inclusions have more serious stress concentration, meaning higher crack initiation potency. However, the value of Ktis still lower than that for subsurface pores. As a result, the pore is the most detrimental defect when Einc/Emis in the range of 0.25 to 2.

Fig. 2. Stress concentration factor Kt distribution as a function of dinc/d values

In addition, the increasing of Einc/Emindicates that the Emtogether with yield strength is decreased. Therefore, the results in Fig. 2 can explain the sensitivity of material strength to defects. It is concluded that the higher the material strength, the higher the crack initiaion potency at soft inclusions. The accords with many VHCF failures originated from micro-defects in higher strength steels[5,14,23]. Whereas for hard inclusions, the materials with lower strength values have higher crack initiation ability. The reduction of Emmay be also related to the crack initiation behavior at high temperature. That is, the matrix softening promotes crack origination in hard inclusions.

3.2 Defect-dependent crack initiation modes

In this paper, as indicated in Fig. 2, the location of the inclusion is determined by the parameter dinc/d whereas the location of Kt(the point with maximum stress concentration)is actually dependent on defect properties. For example,under static loadings, hard inclusions locate maximum stress, and in the case of soft inclusions, Ktoccurs at the matrix. Therefore, the inclusion location dinc/d is not necessarily the same as the location of Kt. Fig. 3(a)illustrates the location change of Ktby using a new parameter D/d. Here, D is the distance from the location of Ktto the specimen surface. For Einc/Em= 2, the highest Ktis not located at specimen surface but on the inclusion, though the corresponding dinc/d is zero. As for soft inclusions and pores, Ktvalues are gradually reduced with D/d increasing from zero to one after which they are almost stable. It is seen that regardless of defect types, the values of Ktin D/d＜ 1 are higher, meaning higher crack initiation potency.

Fig. 3. Location change of Kt and its dependence on defect properties

Another aspect is that the location of maximum Ktis also dependent on defect properties. Fig. 3(b) indicates the variation of maximum Ktand their location D/d as a function of Einc/Em. It can be observed that the values of the maximum Ktare gradually reduced to the lowest(at Einc/Em=1), and then increased in hard inclusions. Correspondingly,the locations of maximum Ktalso transfer from interior matrix(pores) to surface(soft inclusions), and finally subsurface(hard inclusions). As far as pores and soft inclusions are concerned, the maximum Ktis located at the matrix. Therefore, soft inclusions may debond with the matrix, and thus forming notches around soft inclusions(just like pores).

On the other hand, hard inclusions localize stress and thus tend to cracking. Consequently, two mechanisms of interior crack formation occur due to the influence of defect properties, i.e., inclusion-matrix debonding induced crack formation(soft inclusions) and inclusion cracking induced crack initiation(hard inclusions). In fact, both types of interior crack formation have been documented in Ref. [24].Moreover, the maximum Kt, which indicates the starting point for crack initiation, will decide the morphology of interior plane cracks such as the fish-eye shape, as seen in the data collected by SAKAI, et al[5]. In this case, the alteration of fish-eye size will eventually influence the interior crack growth life in the VHCF regime.

3.3 Effect of defect size and depth

Apart from the defect properties, their size and depth also play important roles in interior crack initiation. As for the pore defects, their properties can be regarded as Einc/Em= 0. Fig. 4 depicts Ktversus dinc/d at various pore sizes. It is of interest to note that the distributions of Ktalmost show the same patterns for the pores with different diameters(i.e.,70, 100 and 140 μm). The Ktindependence of circular pore size is in agreement with the work in Ref. [16–17] where stress concentration variation is less profound when the pore diameter is lower than 200 μm. SKALLERUD, et al[25], observed experimentally that pores with a maximum diameter larger than 0.2 mm result in a significant reduction of the lifetime. Nevertheless, XU, et al[17], argued that a larger pore did not necessarily cause a greater stress concentration factor but a much larger region of stress localization. This is helpful to estimate the fatigue life from the viewpoint of the size of casting defects[26].

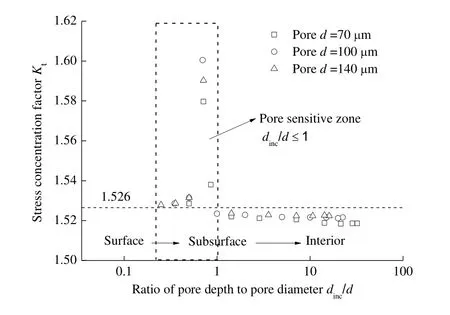
Fig. 4. Kt versus dinc/d at different pore size

Apart from the pore size effect, in Fig. 4, it is observed that the Ktvalues at dinc/d ≤ 1 are relatively higher than those at dinc/d > 1 where the Ktvalues are almost stable.Moreover, the Ktvalues at subsurface pores are considerably larger than those pores at surface. Therefore,dinc/d ≤ 1 is the pore-sensitive zone in which subsurface pores are the most detrimental. Here, the maximum Ktvalues have the similar dinc/d approaching to 0.7. Therefore,the corresponding dincis 49, 70 and 98 μm for pore size of 70, 100 and 140 μm, respectively. This indicates that cracks are most likely to initiate from pores whose distances to specimen surface are below 0.7 times of their diameter.

As for inclusions, two ratios of Einc/Emare selected in the simulation, and the Ktdistributions as a function of dinc/d are shown in Fig. 5. In Fig. 5(a), it is interesting to find that for soft inclusions(Einc/Em= 0.3), with dinc/d decreasing(the inclusions approach to the specimen surface), values of Ktincrease gradually at first and then reach a peak at the specimen subsurface. Maximum Ktis almost a constant for the inclusions with different size, and even has the same location factor, i.e., dinc/d approaches to 0.5. Whereas for hard inclusions(i.e. Einc/Em= 1.7), maximum Ktare located at surface inclusions(dinc= 0) and the curves show valleys in near surface of specimen.

Moreover, Ktdistributions are converged when dinc/d is approximately below 0.76 regardless of inclusion size for both hard and soft inclusions. This is similar to the pore size independence of Ktin Fig. 4. As a result, this region can be called the inclusion size independent zone. In the case of dinc/d > 0.76, the Ktvalues of soft inclusions decrease continuously with dinc/d increasing. At a certain dinc/d, the larger the inclusion size, the higher the degree of stress localization. As a result, cracks are more prone to initiate from larger inclusions. In Fig. 5(a), a dash line denotes the equivalent Ktvalues for different inclusion size.It is observed that larger interior inclusion has the similar Ktto smaller inclusion at lower depth. This means that smaller inclusions at lower depth and larger inclusions at greater depth have equal crack initiation probability. It is therefore concluded that, when soft inclusions are located in the region of dinc/d > 0.76, crack initiation behavior is dependent on both inclusion size and depth. This conclusion has been verified by VHCF test results (Fig.5(b))[21,24]which shows the increasing size of the interior inclusions based on the detailed surface observation of failed specimens.

Also in the area of dinc/d > 0.76, for hard inclusions,however, it is the smaller inclusions that have higher local stresses at given locations. This indicates that smaller hard inclusion has the higher crack initiation potency.Furthermore, unlike the continuous reduction of Ktin soft inclusions, here the Ktvalues present a smaller degree of variation in the whole range of dinc/d, which denotes the lower sensitivity to inclusion size and depth. By comparing with the pore sensitive zone, i.e., dinc/d ≤ 1, the defect sensitive zone for inclusions has been reduced to dinc/d ≤0.76. It is inferred that with Einc/Emincreasing, the range of the defect sensitive zone has been reduced. Therefore, the crack nucleation potency among pores, soft and hard inclusions presents different patterns, and more importantly,the defect size and depth should be comprehensively considered.

Fig. 5. Kt distribution and its size variation with dinc/d

3.4 Effect of inclusion shape

In commonly used materials, some of the inclusions are elliptical. In the simulation process, elliptical inclusions are modeled by reducing the short-axis length b while keeping the long-axis length a as a constant(i.e., a = 140 μm). As a result, the ratios of a/b is increased. Fig. 6 indicates Ktversus dinc/a with a/b in the range of 1–8. With a/b increasing, Ktdistribution at a/b = 2 is similar to that at a/b= 1. It is therefore concluded that the inclusion shape with a/b in the range of 1–2 almost have equal crack initiation potency. As mentioned before, the inclusion size independent zone is dinc/d ≤ 0.76. However, the results in Fig. 6 show that the zone in dinc/a ≤ 0.76 is inclusion shape dependent since Kttends to decrease as b is reduced. This means that elliptical inclusions with a/b > 2 have lower crack initiation potential. It is therefore inferred that the short-axis length b determines the overall possibility for crack nucleation.

The effect of inclusion shape on Ktis critical to understand the relative significance of a and b in crack initiation. It is worth noting that the location of peak Ktat various a/b is independent of the inclusion shape. The ratio of dinc/a at the peak Ktis close to the value of dinc/d for circular soft inclusions(Fig. 5(a)) (almost fixed at dinc/d of 0.5), but lower than that in pores, i.e., dinc/d is 0.7 at peak Kt(Fig. 4). It is concluded that cracks are most likely to initiate from one of the soft inclusions whose distance to specimen surface are 0.5 times as large as their diameter.

In fact, as shown in Fig. 5(a), the values of dinccorresponding to the maximum Ktare different in various soft inclusions, i.e., dincis increased when the inclusion size is varied from 70 to 140 μm. Similar results have been observed in pore type defects in Fig. 4. All these results indicate that the locations for the maximum stress localization at soft inclusions are mostly dependent on the long-axis length, regardless of their shape. It is also worth noting in Fig. 6 that when a/b equals to four or eight,interior inclusions have larger Ktthan those of surface inclusions(as shown by the short dash lines). That is, the reduction of b increases the likelihood of interior initiation,and thus contributes to crack formation transition from surface to interior.

Fig. 6. Influence of inclusion shape on Kt

3.5 Effect of residual stress

In practice, residual stress(RS) in materials and structures will change local stress state, and thus influence the fatigue properties[27]. It is generally accepted that tensile RS is detrimental while compressive RS is beneficial.Recently, some experimental work has focused on the role of the RS in altering the shape of S−N curve in the VHCF regime[28–29]. In this paper, numerical simulation is employed to quantitatively evaluate the role of the RS in fatigue crack initiation transition behavior in the specimens containing hard or soft inclusions. As indicated in section 2,RS is obtained by imposing a moment load Mz. The value of the moment load influences the RS distribution. It is assumed that the RS introduced by this method and other surface treatment techniques play the same roles in the fatigue crack initiation process.

Fig. 7(a) shows RS distribution in specimens without inclusions at different Mz. The RS, which is output from the simulations, locates at the centerline of minimum section of the models and varies as a function of the distance of node to specimen surface D*. The values of the RS(σRS) are normalized by the yield strength σyof the matrix at room temperature. It is observed that the RS is compressive at the specimen surface, and then shifts to tensile stress before approaching zero at the specimen center. Both the compressive RS at surface σRS,surand the RS distribution are dependent on Mz. The higher the values of Mz, the larger the σRS,sur. The largest tensile RS σRS,tenlocates at a distance of 1.9 mm below surface at Mz1. With Mz1decreased to Mz3, the corresponding σRS,suris reduced and the maximum σRS,tenlocates at approximately 1.2 mm below surface. Fig. 7(b) further indicates the RS distribution along the specimen cross section with inclusions. It is observed that the existence of inclusions only alter the local RS around inclusions, leaving little influence on RS in other areas. This is associated with the assumption of elasticity of the inclusions. In this case, the RS around inclusions are higher than the yield strength of the matrix.

Fig. 7. RS distribution in specimens with and without inclusions

Influence of the RS on maximum stress concentration factor Kt,maxaround inclusions is presented in Fig. 8. Here,Mises stresses around inclusions are normalized. For soft inclusions(Einc/Em= 0.5) with σRS,sur/σyof −0.64, the largest Kt,maxlocates at 1.5 mm below surface, which is related to interior σRS,ten. As a result, inclusion with a depth of 1.5 mm below surface has the highest crack initiation potency. It is worth noting that the subsurface inclusion at a depth of 200 μm also has higher Kt,max, forming another potential site for crack nucleation. In this case, the local σRS,tenaround inclusions(as shown in Fig. 7(b)) is responsible for the slightly increased Kt,max.

Fig. 8. Influences of the RS on maximum Kt around inclusions

Actually there are many factors influencing the reduction of RS(often called relaxation) including the initial stress state, the actual material and microstructure, as well as the loading conditions[30]. In this work, though the relaxation process of the RS is not modeled under static loading, it can be quantitatively evaluated by the values of Mz. It is observed in Fig. 8 that with the decreasing of σRS,sur, the values of Kt,maxreduce accordingly, and the peak Kt,maxis also located at 1.5 mm below surface. However, higher stress localization disappears at subsurface inclusions,which makes interior inclusions become unique crack initiation sites. It is therefore concluded that in the case of soft inclusions, the RS relaxation process reduces the values of Kt,maxbut does not change the location of the peak Kt,max. This means that interior inclusions are always the potential site for crack initiation. Nevertheless, when the RS is completely relaxed, i.e., the specimens are free from RS, as illustrated in Fig. 5(a), the maximum Ktat soft inclusions occurs at the specimen subsurface. Therefore,the RS is helpful to the transition of crack initiation site from specimen surface to interior inclusions.

In the case of hard inclusions(Einc/Em= 2), for the same values of σRS,sur, the Kt,maxin each inclusion(the same location) are larger than those for soft inclusions. The higher the σRS,sur, the larger the values of Kt,max. Of all the inclusions investigated, the highest Kt,maxoccurs at the hard inclusions with σRS,sur/σyof −0.64. The inclusion property is relatively more important because the values of Kt,maxat hard inclusions with σRS,sur/σyof −0.33 are higher than those at soft inclusions with σRS,sur/σyof −0.43. It is therefore concluded that the decreasing ability of crack initiation from hard inclusions due to the relaxation of RS is not as large as that from soft inclusions.

It is also worth noting that the peak Kt,maxare also located at 1.5 mm below surface, and subsurface inclusions with dincof 200 μm also undergo higher localized stress.This indicates that with the influence of the RS, hard inclusions, especially those inclusions at dincof 1.5 mm or 200 μm are more prone to initiate cracks under cyclic loading. Interestingly, the highest Ktalways locates at surface inclusions in specimens without RS(in Fig. 5(a)).Therefore, for hard inclusions, the RS is also expected to transfer fatigue crack initiation from surface inclusions to the inclusions that are subsurface or interior.

In should be noted that the RS relaxation is related with such factors as stress amplitude and high temperature.Under higher load levels, i.e., in the high cycle fatigue regime, the RS relaxes quickly in the first few cycles and then becomes stable. Therefore, the final crack initiation site is dependent on the competition between specimen surface condition and the RS. In this case, duplex S-N curves are obtained as reported in Ref. [28]. If the stress amplitude is quite lower, the RS cannot relax easily, and thus interior inclusions are the dominated crack initiation site. As a result, internal fracture can be regarded as inherent in the material for VHCF, as argued by SHIOZAWA, et al[23].

4 Conclusions

(1) Crack initiation potency can be increased with the enhancement of property mismatching between matrix and defects. Materials with higher strength are sensitive to soft inclusions, whereas hard inclusions are most probable to initiate cracks in lower strength materials.

(2) The stress localization at inclusions determines the interior crack initiation modes, i.e., inclusion-matrix debonding for soft inclusions while inclusion cracking induced crack initiation for hard inclusions, and eventually influenced the morphology and lifetime of interior crack growth in the VHCF regime.

(3) Their exists a pore insensitive zone for crack nucleation, with the most potential site occurred at the depth value that is 0.7 times as large as their diameter.Crack initiation is independent of inclusion size when the inclusion depth is not more than 0.76 times of its diameter.Otherwise, crack formation can transfer from soft inclusion at subsurface to interior larger one.

(4) The long-axis length of elliptical inclusions, which controls the site of peak stress concentration, is decisive in influencing crack initiation potential. Decreasing the short-axis length can reduce crack nucleation potential and promote interior crack formation as well.

(5) The compressive RS at surface is helpful to shift crack initiation from surface to interior inclusions. Some relaxation of RS cannot change the inherent crack initiation site from interior inclusions in the VHCF regime.

[1] SONSINO C M. Course of SN-curves especially in the high-cycle fatigue regime with regard to component design and safety[J].International Journal of Fatigue, 2007, 29(12): 2246−2258.

[2] BOWLES C Q, SCHIJVE J. The role of inclusions in fatigue crack initiation in an aluminum alloy[J]. International Journal of Fracture,1973, 9(2): 171−179.

[3] JANEIRO R P, EINSTEIN H H. Experimental study of the cracking behavior of specimens containing inclusions(under uniaxial compression)[J]. International Journal of Fracture, 2010, 164:83−102.

[4] MURAKAMI Y. Metal fatigue-effects of small defects and nonmetallic inclusions[M]. Kidlington: Elsevier, 2002.

[5] SAKAI T, SATO Y, OGUMA N. Characteristic S−N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue[J]. Fatigue & Fracture of Engineering Materials &Structures, 2002, 25(8−9): 765−773.

[6] BAYRAKTAR E, GARCIAS I M, BATHIAS C. Failure mechanisms of automotive metallic alloys in very high cycle fatigue range[J].International Journal of Fatigue, 2006, 28(11): 1590−1602.

[7] ZHU X, SHYAM A, JONES J W, et al. Effect of microstructure and temperature on fatigue behavior of E319-T7 cast aluminum alloy in very long life cycles[J]. International Journal of Fatigue, 2006, 28:1566−1571.

[8] YU Y, GU J L, SHOU F L, et al. Competition mechanism between microstructure type and inclusion level in determining VHCF behavior of bainite/martensite dual phase steels[J]. International Journal of Fatigue, 2011, 33(3): 500−506.

[9] ZHANG J M, LI S X, YANG Z G, et al. Influence of inclusion size on fatigue behavior of high strength steels in the gigacycle fatigue regime[J]. International Journal of Fatigue, 2007, 29(4): 765−771.

[10] MUGHRABI H. On “multi-stage” fatigue life diagrams and the relevant life-controlling mechanisms in ultrahigh-cycle fatigue[J].Fatigue & Fracture of Engineering Materials & Structures, 2002,25(8−9): 755−764.

[11] FARIDA B, BOUALEM S, MECIRDI M E A, et al. 3-D finite element analysis of stress concentration factor in spot-welded joints of steel: The effect of process-induced porosity[J]. Computational Materials Science, 2011, 50(4): 1450−1459.

[12] MAYER H, PAPAKYRIACOU M, ZETTL B, et al. Influence of porosity on the fatigue limit of die cast magnesium and aluminium alloys[J]. International Journal of Fatigue, 2003, 25(3): 245−256.

[13] CHANDRAN K S R, CHANG P, CASHMAN G T. Competing failure modes and complex S-N curves in fatigue of structural materials[J]. International Journal of Fatigue, 2010, 32(3): 482−491.

[14] MURAKAMI Y, KODAMA S, KONUMA S. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions[J]. International Journal of Fatigue, 1989, 11(5): 291−298.

[15] BORBÉLY A, MUGHRABI H, EISENMEIER G, et al. A finite element modelling study of strain localization in the vicinity of near-surface cavities as a cause of subsurface fatigue crack initiation[J]. International Journal of Fracture, 2002, 115: 227−232.

[16] GAO Y X, YI J Z, LEE P D, et al. The effect of porosity on the fatigue life of cast aluminium-silicon alloys[J]. Fatigue & Fracture of Engineering Materials & Structures, 2004, 27(7): 559−570.

[17] XU Z, WEN W, ZHAI T. Effects of pore position in depth on stress/strain concentration and fatigue crack initiation[J].Metallurgical and Materials Transactions A, 2011, 43(8): 2763−2770.

[18] FENG L, XUAN F Z. Effect of non-metallic inclusions on the local stress concentration within materials[J]. Journal of Mechanical Engineering, 2013, 49(8):41−48. (In Chinese)

[19] GALL K, HORSTEMEYER M F, DEGNER B W, et al. On the driving force for fatigue crack formation from inclusions and voids in a cast A356 aluminum alloy[J]. International Journal of Fracture,2001, 108(3): 207−233.

[20] PRZYBYLA C, PRASANNAVENKATESAN R, SALAJEGHEH N,et al. Microstructure-sensitive modeling of high cycle fatigue[J].International Journal of Fatigue, 2010, 32(3): 512−525.

[21] ZHU M L, XUAN F Z, DU Y N, et al. Very high cycle fatigue behavior of a low strength welded joint at moderate temperature[J].International Journal of Fatigue, 2012, 40: 74−83.

[22] PETIT J, SARRAZIN-BAUDOUX C. An overview on the influence of the atmosphere environment on ultra-high-cycle fatigue and ultra-slow fatigue crack propagation[J]. International Journal of Fatigue, 2006, 28(11): 1471−1478.

[23] SHIOZAWA K, LU L. Very high-cycle fatigue behaviour of shot-peened high-carbon-chromium bearing steel[J]. Fatigue &Fracture of Engineering Materials & Structures, 2002, 25(8−9):813−822.

[24] ZHU M L, XUAN F Z, CHEN J. Influence of microstructure and microdefects on long-term fatigue behavior of a Cr-Mo-V steel[J].Materials Science and Engineering A, 2012, 546: 90−96.

[25] SKALLERUD B. Fatigue life assessment of aluminum alloys with casting defects[J]. Engineering Fracture Mechanics, 1993, 44(6):857−874.

[26] COUPER M J, NEESON A E, GRIFFITHS J R. Casting defects and the fatigue behaviour of an aluminium casting alloy[J]. Fatigue &Fracture of Engineering Materials & Structures, 1990, 13(3):213−227.

[27] MIAO H, ZUO D W, WANG M, et al. Numerical calculation and experimental research on residual stress in precipitation-hardening layer of NAK80 steel for shot peening[J]. Chinese Journal of Mechanical Engineering, 2011, 24(3): 439−445.

[28] SHISOZAWA K, MURAI M, SHIMATANI Y, et al. Transition of fatigue failure mode of Ni-Cr-Mo low-alloy steel in very high cycle regime[J]. International Journal of Fatigue, 2010, 32(3): 541−550.

[29] SHIMATANI Y, SHIOZAWA K, NAKADA T, et al. The effect of the residual stresses generated by surface finishing methods on the very high cycle fatigue behavior of matrix HSS[J]. International Journal of Fatigue, 2011, 33(2): 122−131.

[30] ZHUANG W Z, HALFORD G R. Investigation of residual stress relaxation under cyclic load[J]. International Journal of Fatigue,2001, 23: S31−S37.