基于死区逆变换补偿的纯电动转向系统控制方法设计

梁松峰，董铸荣，2，邱 浩

(1. 深圳职业技术学院 汽车与交通学院，广东 深圳 518055；2.北京交通大学 机电控制工程学院，北京 100044)

0 引 言

面对环境污染和能源危机两大难题，电动汽车因其清洁无污染、能量来源多样化等优点，得到逐步的推广。区别于电动助力转向系统，纯电动转向系统全部转向动力由电机提供，采用线控的方式工作[1]。

纯电动转向系统的优点是：①取消了汽车上原有的转向机械，使转向系统结构简化为“方向盘-ECU-电机”的结构；②转向机构可以灵活布置，可以安装在前轮或者后轮，甚至四轮转向；③与电动汽车的驱动系统配合可以实现“原地转向”、“横拨”等传统汽车无法实现的功能[2]。

这类转向系统的缺陷也比较突出：①转向负载比较重同时不能借助机械、液压等动力，电机需要输出较大的扭矩，虽然借助减速机构可以解决问题，但是减速机构的速比不能太大，否则会严重影响转向的相应速度，因此需要在转矩和转速这两个方面进行平衡；②由于车轮与车轮之间不存在机械连接，左右轮的转角差需要有ECU来控制，控制稍有偏差便会导致汽车无法高速行驶；③由于电机的负荷较重，加上减速机构的摩擦等因素，存在较大的死区，在ECU实施控制时，电机的转速与控制信号并不成正比例关系，使控制达不到理论、仿真的控制效果。

笔者通过采集试验车转向系统的相关数据以及分析转向系统的结构和工作原理，获得了转向系统各组成部分的数学模型；基于这些数学模型使用MATLAB进行仿真，比较“普通PID控制”与“基于死区逆变换补偿PID控制”[3]在控制效果上的区别；将仿真使用的数学模型以及参数移植至试验车上的ECU进行验证。实车验证结果表明：笔者提出的控制方法能够消除死区带来的不良影响，提高了转向控制的质量。

1 转向系统的实物与结构

项目研究平台为“四轮独立驱动线控转向电动汽车”，该车由奇瑞QQ车改装而成，改装的过程把原QQ车的发动机、转向系统、悬架去掉，然后课题组自己设计驱动、转向、悬架并重新布置安装，形成了一部电动驱动电动转向的试验车(图1)[4]，装后的试验车的总质量为1 144 kg，轴距为1 318 mm，轮距为2 114 mm。

图1 试验车Fig.1 The test vehicle

根据系统的设计，画出转向控制系统结构框图，如图2。图中，θ为方向盘角度，控制系统根据该角度计算对应的车轮应有的转角，并与车轮转角α比较，经过控制算法计算出控制量u，传递给控制器，经过电机、减速机构、齿轮机构作用到车轮上，形成转角的闭环控制。

图2 转向控制系统结构Fig.2 Structure of steering control system

2 转向控制系统数学模型

基于理论分析以及仿真确定参数的需要，笔者经过实验数据采集、分析与理论推导获得了角速度-车轮转角的数学模型以及转向机构数学模型，两者一起构成控制系统的控制对象。本系统是计算机控制系统，控制算法、控制对象都必须使用离散数学模型来描述。

2.1 角速度与车轮转角的离散数学模型

角速度的定义如式(1)，在计算机控制系统中，该式离散化的描述形式如式(2)，由式(2)可以推导出描述车轮转角与角速度的关系的差分方程，如式(3)：

(1)

(2)

(3)

2.2 转向机构的离散数学模型

图3 转向机构特性Fig.3 Characteristics of the steering mechanism

(4)

在转向系统中，由试验数据获得的式(4)的各参数如下：Δ+=0.47 V，K+=45 (°)/(s·V)，Δ-=-0.45 V，K-=41 (°)/(s·V)。

3 死区逆变换补偿方法

死区逆变换补偿的本质是把带有死区的非线性的系统通过逆函数补偿的处理变成线性系统，经过变换后可以使PID控制发挥最好的效果，并且能比不变换的系统更快消除静差[6]。死区逆变换补偿的是一种软件算法，它能够在不改变硬件系统的情况下，消除执行机构死区带来的影响，使得在实施控制的时候，控制对象对于PID算法来说呈良好的线性关系，它在控制系统中的位置如图4。

图4 死区逆变换补偿在系统中的位置Fig.4 Position of the dead-zone inverse transforming compensation in the system

死区逆变换补偿按照如下步骤来进行：

3)求取死区逆变换补偿函数，见式(5)：

u′=h(u)=g-1(f(u))

(5)

对逆变换补偿方法的证明如式(6)：

(6)

以文中控制对象为例，其死区逆变换函数补偿为：

(7)

死区逆变换补偿的过程可以用图5说明。可以看出，经过逆变换后，PID控制对象的死区被消除了，呈良好的线性。在文中转向系统中，选取K=1。

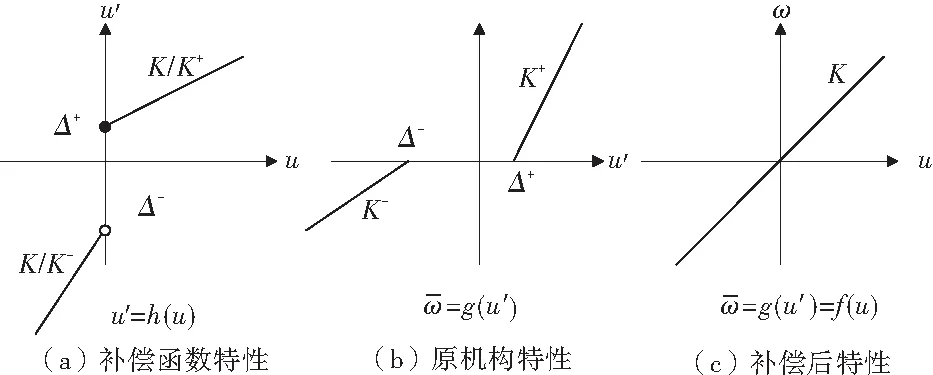
图5 死区逆变换图解Fig.5 Diagram of dead-zone inverse transforming

4 死区逆变换补偿方法的MATLAB 仿真验证及参数整定

将文中推导的数学模型以及控制算法输入MATLAB进行软件仿真[7]，获得了两种情况下的控制效果。

按照普通PID控制方法，不对死区处理时，由于存在死区，并且死区比较大，所以控制结果是存在比较大的静差，为了消除静差必须增大比例kp或者减少积分时间ti，这样造成较大的超调，减小超调的方法是增大微分时间，这样又出现了抖动[8]，因此效果总不太理想，图6是相对好一些的控制效果，静差=0.83～5.97°，此时PID控制参数为：ts=0.5 s,kp=0.025,ti=5 s,td=1 s。

图6 一般PID控制效果Fig.6 Control effect of general PID

经过逆变换补偿消除死区后，由于死区被消除，控制效果的静差比较小，通过调节其他参数可以获得比较好的控制效果，静差为0.04～0.13°，如图7。此时PID参数为：ts=0.5 s,kp=0.7,ti=600 s,td=0.1 s。

图7 带死区逆变换补偿的PID控制效果Fig.7 Control effect of PID with dead-zone inverse transforming compensation

5 实车验证

将MATLAB仿真确定的参数用于实车的控制，控制过程中的转角目标值以及转角反馈值通过ECU的串行通信接口实时上传至电脑，将电脑接收到的数据输入Excel画出曲线可以看到控制的效果。

图8为使用一般PID的控制实车实验效果，试验过程中发现，由于死区影响比较显著，图6仿真的比例系数kp偏小，实验中将kp修正为0.05，即图8是在控制参数为ts=0.5 s,kp=0.05,ti=5 s,td=1 s时获得的控制效果，此时静差为3.95～4.24°。

图8 一般PID实车控制效果Fig.8 Control effect of general PID real vehicle

图9为使用一般PID的控制实车实验效果。试验使用的控制参数与图7仿真参数完全一致。但是，把该方法应用于实车时发现，如果直接运用式(7)，有时候车轮会有小幅抖动。分析可知这是由于机械润滑状况与电路温度发生漂移，式(7)中的Δ+与Δ-存在小幅漂移，如果实际的死区比算法中的死区小，控制系统会输出比实际需要大的控制量，导致出现抖动。因此，在实验时对式(7)进行了改进，变为式(8)的形式：

(8)

式(8)把算法中的死区修改为测量死区的0.95倍，即留了0.05Δ的控制裕度，以防实际死区缩小。也就是说，使用式(8)做死区逆变换补偿后，实质上还有0.05Δ左右的死区(该死区可能随着机械润滑状况或者电路温度漂移而变化)，但是从实际控制效果图可以看出该方法实质上消除了95%的死区范围，同时获得了更加稳定、更小静差的控制效果，此时静差为0.28～0.42°。

图9 一般PID实车控制效果Fig.9 Control effect of general PID real vehicle

6 结 语

电动汽车中所需的动力基本上都是使用电机来控制的，电机执行机构在负载较重时会有比较大的死区，死区的存在影响控制效果容易产生较大的静差。笔者建立了一种纯电动转向系统的数学模型，以MATLAB为工具，对比了使用“死区逆变换补偿”方法前后的转向控制效果，并将MATLAB仿真的数学模型以及参数应用于实车。经过实验验证可知，笔者提出的“死区逆变换补偿”方法是行之有效的，将它应用到带死区的转向系统控制中可以减小死区带来的偏差，提高控制的质量。

[1] 苑林.汽车电动转向系统的研究[D].吉林:吉林大学,2007.

Yuan Lin. Study on Vehicle Electric Power Steering System [D]. Jilin: Jilin University, 2007.

[2] 董铸荣,贺萍,邱浩,等.各轮独立转向及驱动的电动汽车及其转向与驱动控制方法:中国,200910310310.2[P].2010-06-02.

Dong Zhurong, He Ping, Qiu Hao, et al. System and Controlling Method for Independent Steering and Independent Driving of Automobile Wheel: China,200910310310.2 [P].2010-06-02.

[3] Tian M, Tao G. Adaptive Output Dead-Zone Compensation[C]. San Diego, California, USA: The 36thConference on Decision & Control, 1997: 1157-1161.

[4] 邓志君,董铸荣,马德粮.电动轿车独立转向轮悬架设计[J]. 汽车技术,2010(12):37-41.

Deng Zhijun，Dong Zhurong，Ma Deliang. Suspension design of the independent steering wheel for electric car[J]. Automobile Technology, 2010(12): 37-41.

[5] 文彩虹,蒋东方,晁敏. 直流力矩电机控制死区的在线检测与补偿[J]. 测控技术,2010(4):35-38.

Wen Caihong, Jiang Dongfang, Chao Min. On-line dead-zone detection and compensation for DC torque motor control systems[J]. Measurement & Control Technology, 2010(4): 35-38.

[6] Huang R N，Lou Y J，Chi G X. Research on Servo Feeding System of Micro WEDM[C]. Changsha，Hunan，China: 2010 International Conference on Digital Manufacturing & Automation, 2010: 271-274.

[7] 刘金琨. 先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.

Liu Jinkun. Advanced PID Control and MATLAB Emulation [M]. Beijing: Publishing House of Electronic Industry,2003.

[8] 吴麒,王诗宓. 自动控制原理:上册[M].2版.北京:清华大学出版社,2006:125-133.

Wu Qi，Wang Shimi. Principle of Automatic Control: PartⅠ[M]. 2nd ed. Beijing: Tsinghua University Press, 2006.