基于分形理论的水流混掺长度垂线分布公式修正
吴立春,倪志辉
(1.重庆第二师范学院,重庆 400067;2. 重庆交通大学 国家内河航道整治工程技术研究中心水利水运工程教育部重点实验室,重庆 400074;3. 重庆交通大学 西南水运工程科学研究所,重庆 400016)
0 引 言
混掺长度是水流紊动的重要特性,其垂线分布规律与水流阻力、泥沙运动及环境工程均密切相关,直接影响着底床冲刷和淤积的演变过程。因此,研究挟沙水流混掺长度的垂线分布规律既有重要的理论意义,又有助于解决实际工程问题。为此,国内外许多学者进行了大量测量和分析工作[1-5],这些研究大都通过明渠、圆管、平板边界层等的水流试验展开。L.Prandtl[1]参照分子碰撞中自由行程的概念引入混掺长度概念,表示当流体质点从速度的层因脉动而跳至另一层时,流体质点的原有动量刚好转换并等于新的一层处的动量。该两层之间的距离称为混掺长度l。根据L.Prandtl混掺长度理论,在近壁紊流中,假定l与从固体壁面算起的法向距离y成比例,即:
l=κy
(1)
式中:l为混掺长度,它与流动情况有关,可由试验确定;κ为卡门常数,对于清水水流情况,κ≈ 0.4。
对于充分发展的管流和明渠,J.Nikuradse[2]提出的混掺长度分布公式:
(2)
式中:R为管的半径或明渠的水深。
在靠近壁面的区域,式(2)给出的结果与式(1)一致。但是,在非靠近壁面的区域,黏性起决定性的作用,通常采用Van Driest[3]公式修正混掺长度的线性关系式:
(3)
式中:A=26;τw为壁面剪应力。
为了避免确定l的计算过程过于繁琐,Von Karman曾建议将l与时均流速的分布按式(4)建立联系:
(4)
式(4)对于近壁水流可得出较好的结果,但缺少普适性。例如,在射流和尾迹中,速度剖面含有拐点,由式(4)会得出无限大的混掺长度。因此,Von Karman公式极少采用。
也有学者通过利用流速梯度分布公式来推导挟沙水流沿整个水深范围内的混掺长度[4-5],在主流区,忽略黏滞切应力,有:
(5)
由于在主流区,挟沙水流紊动切应力基本上是线性分布:
(6)
式中:τb为床面剪切应力,τb=ρ|u*|u*(ρ为水流密度,u*为床面摩阻流速);y为垂向坐标;D为水深。
联立式(5)、式(6)得到:
(7)
由此可见,混掺长度l给予不同的假定,将会得出各种不同的流速分布式。对于简单的剪力层型的流动,不同形式的水流可采用不同的经验常数。但对于紊动输运过程占有重要地位的复杂的水流,则很难确定l。为此,笔者以挟沙水流混掺长度的运动机理为基础,从分形标度的角度探讨挟沙水流混掺长度垂线分布模式,并采用最小二乘法和相应的边界条件,确定分布式的系数。利用现场资料和试验数据进行了验证,并与其它公式计算结果相比较,表明文中公式不仅表达式简洁,而且可以较好地反映挟沙水流混掺长度垂线分布模式特征。
1 公式推导
假设混掺长度按以下方式定义:设一流体块团,以其原有的时均速度运动,由于紊动,该块团在横向由y1运动到y2。在y2点,块团原有速度与周围介质时均速度之差为▽U。如果在y2点的平均横向脉动速度恰为▽U,则将距离y2-y1定义为混掺长度l。由于挟沙水流的含沙量分布不均匀,水流紊动作用等因素,挟沙水流中的“漩涡”水团其实是一种无规则运动,因此用分形理论描述实际运动轨迹长度l和水平投影长度间的关系。在图1的分形结构中,当分形迭代次数i= 0时,图形为直线;当i=1时,0~l1间线形不变,而l1和l2间的线形由直线l1~l2变为折线段l1~l3~l2,l3为l1~l2线段上方(或下方)任意处引入的一点。按此规则分形迭代,图1(c)、(d)中,虚线代表i-1次迭代后的形状,而实线则是i次迭代后的形状。
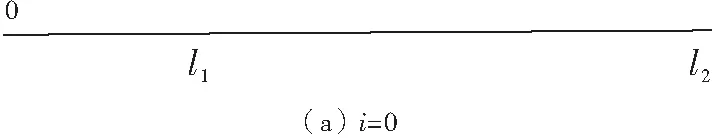

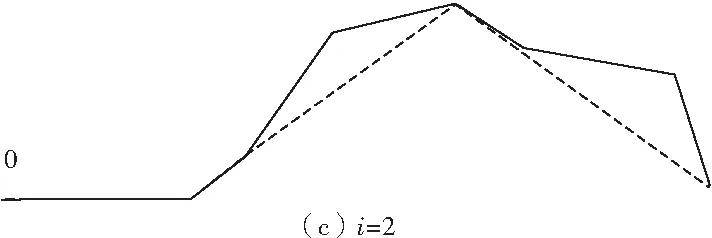
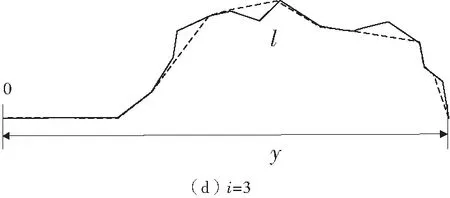
图1 水团的实际运动轨迹长度与水平映射距离示意Fig.1 Water masses in the actual motion path length and level mapping distance
i次分形迭代后,折线的长度与水平映射距离的平均关系为:
li=β-iyi
(8)
式中:l为分形迭代后折线的实际长度;yi是相应的投影长度;β为反映l与yi平均关系的参数。
由分形理论知,对任一的分形迭代i,长yi的线段个数可表示为:
(9)
式中:D为分形维数,对于1维情况,0 由式(8)和式(9)知,水团的实际运动轨迹长度l与水平映射距离y之间的平均关系可以描述为: (10) 式中:A为比例常数;l为混掺长度;y为水深。 式(10)即为笔者所建立的挟沙水流混掺长度指数公式。 垂直各层上的实测值在理论上应满足式(10),但由于实测值本身即存在误差且忽略它们之间非线性作用等因素,各层的理论值与实测值之间也就存在误差。由于未知量有2个(A和D),而一般实测数据不一定有2层,因而,笔者采用枚举法结合最小二乘法[6-8]的方法求解。步骤如下: 1)建立目标函数 (11) 式中:yi表示近底第i层水深;li表示对应的混掺长度值。 2)列举分形维数D,从0.000 1~1,增量设为0.000 1,即共10 000组。 3)对任一个D的枚举值,在目标函数取极小值时满足式(12),求解得出A: (12) 式中:n代表垂线用来拟合的点数。 4)计算10 000组D对应10 000个f的最小值,使目标函数取极小值,则各层理论值与实测值的总误差将达到最小,从而得出D。 为了验证笔者所建式(10)的合理性,采用图2~图5[2,9-11]的现有典型实验数据对公式进行验证,并与式(1)、式(7)计算结果进行比较。图中,实点代表实验值,细实线代表公式(1)拟合值,虚线代表式(7)拟合值,粗实线代表笔者提出模式与实测值的最佳拟合值。 图2 与Nikuradse实验数据的比较Fig.2 Comparison of experimental data with Nikuradse 图3 与Vanoni实验数据的比较Fig.3 Comparison of experimental data with Vanoni 图4 与Einstein和Chien实验数据的比较Fig.4 Comparison of experimental data with Einstein and Chien 图5 与Castro和Epik实验数据的比较Fig.5 Comparison of experimental data with Castro and Epik 由图2~图5可以看出,笔者提出的式(10)的计算值均比式(1)和式(7)更接近实测值,说明前者精度更高,更能反映出挟沙水流混掺长度垂线分布的规律。 长期以来,混掺长度常假设采用简单的经验公式确定l。对于自由层,可假设l在横断面上保持为常数,且与当地层厚δ成正比,其比例因子取决于自由流的类型。由此可见,混掺长度模型缺少通用性,对于不同形式的水流需采用不同的经验常数。这是混掺长度理论中忽略了紊动量的扩散输运和对流输运的必然结果。从文中挟沙水流的混掺长度的运动机理出发,结合水流紊动理论和分形理论推导了一种新的混掺长度垂线分布模式。由表1可以看出,笔者提出的式(10)计算拟合的参数A和D,其取值范围均为0 表1 各组实验数据分形维数D和A值 (续表1) 实验组次分形维数DAEinstein和Chien(1955)(a)C⁃130.01750.4026(b)S⁃110.07980.2637(c)S⁃130.09030.1541(d)S⁃150.45730.0297Castro和Epik(1996)(a)0.34510.1203(b)0.26430.2173(c)0.71150.1735 从表1中第3组Einstein和Chien (1955)的资料可以看到,实验条件为清水状态C-13组时,D=0.017 5,1-D≈1,A=0.402 6,式(10)退化为Prandtl公式(l=ky,k通过实验知约为0.40~0.41)。 为了分析含沙量对混掺长度的影响,笔者从Einstein和Chien (1955)实验数据中摘录了实测含沙量,见表2。 表2 公式(10)中参数D与含沙量比较 从表2可见,当参数D越接近0时,水流中含沙量越少。参数D与含沙量存在正比关系,D值越大,含沙量也越大,反之亦然。因此,结合公式(10)可得:混掺长度与含沙量成反比,含沙量越大,则混掺长度越小。 垂向上某一位置处可能出现的不同尺度紊动漩涡大小的平均量度即为该位置处的混掺长度[13]。混掺长度是所有漩涡的平均量度,而几乎所有尺度的漩涡都参与动量传递,水体则是这些紊动的载体[14]。钱宁[15]认为:伴随着挟沙水流黏性的增加,小尺度的漩涡会消失不见。 混掺长度与漩涡能携带的泥沙量有一定相关性,在宏观上表现为和泥沙浓度相关[16]。泥沙对紊动的制约作用随着浓度的增大越来越明显,而混掺长度则随着浓度增大而减小。泥沙的浓度分布通常表现为上小下大,浓度梯度对混掺起到抑制作用。这种抑制作用对泥沙本身的影响可能更为明显,因此将导致混掺长度的进一步减小。在泥沙浓度足够大,浓度梯度的抑制作用足够明显的情况下,水流的混掺长度可能会小于清水体混掺长度(由表1也可比较得出)。挟沙水流的混掺长度小于清水体混掺长度的现象,在细颗粒泥沙中更容易表现出来。 以挟沙水流混掺长度的运动机理为基础,从分形标度的角度出发去探讨挟沙水流混掺长度垂线分布模式,并采用最小二乘法和相应的边界条件,确定了分布式的系数。利用现场资料和试验数据进行了验证,并与其它公式计算结果相比较,得出如下结论: 1)笔者提出的指数公式比线性公式和其它公式更接近实测值,精度更高。表明该公式可以较好地反映挟沙水流混掺长度垂线分布特征。 2)笔者提出的公式表达式简洁,原理简单、过程合理、结果可信, 建立的挟沙水流的混掺长度指数公式具有一定的合理性。 3)讨论了含沙量与混掺长度的关系,即含沙量越大,混掺长度越小。这对进一步研究挟沙水流的流速垂线分布提供了有力的数据依据和研究价值。 [1] Prandtl L.Uber die ausgebiidete turbulenz [J].Zeitschrift für Angewandte Mathematik und Mechanik, 1925, 5: 136-139. [2] Nikuradse J.粗糙管中水流的规律[M].北京:水利出版社,1957. Nikuradse J.Stromrngsgesetze in Rauhen Rohren [M].Beijing:Water Conservancy Press,1957. [3] Van Driest E R.On turbulent flow near a wall [J].Journal of the Aeronautical Sciences, 1956, 23(11): 1007-1011. [4] 倪晋仁,王光谦,张红武.固液两相流基本理论及其最新应用[M].北京:科学出版社,1991. Ni Jinren,Wang Guangqian,Zhang Hongwu.Basic Theory of Two-Phase Flow and Its New Application [M].Beijing:Science Press,1991. [5] 张小峰,谈广鸣. 非均匀沙含沙量沿垂线分布特征[J].水利学报,1992(10):48-52. Zhang Xiaofeng,Tan Guangming.Non-uniform sediment characteristics of vertical distribution of concentration [J].Journal of Hydraulic Engineering,1992(10): 48-52. [6] Song Z Y,Yan Y X,Hao J L,et al.Study on the log-linear velocity profile of near-bed tidal current in estuarine and coastal waters [J].China Ocean Engineering, 2006, 20(4): 573-584. [7] Ni Zhihui,Song Zhiyao,Wu Lichun.An approach to separating the current velocity in estuarine and coastal waters [J].Journal of Hydrodynamics, 2009, 21(4): 512-519. [8] 倪志辉,吴立春,宋志尧.近岸海域海面风速分布的预测方法研究[J].空气动力学学报,2010,28(5):547-552. Ni Zhihui,Wu Lichun,Song Zhiyao.A method of wind velocity distribution above the sea surface in near-shore waters [J].Acta Aerodynamica Sinica,2010,28(5):547-552. [9] Vanoni V A.Transportation of suspended sediment by water [J].Transactions of ASCE,1946,111: 67-133. [10] Einstein H A.Effect of Heavy Sediment Concentration Near the Bed on the Velocity and Sediment Distribution [M].Berkeley,California: Institute of Engineering Research,University of California,1955. [11] Castro I P,Epik E. Boundary-layer relaxation after a separated region[J].Experimental Thermal and Fluid Science,1996,13(4):338-348. [12] 杨大升,刘余滨,刘式适.动力气象学[M].北京:气象出版社,1983. Yang Dasheng,Liu Yubin,Liu Shishi. Dynamic Meteorology [M].Beijing: China Meteorological Press,1983. [13] 倪志辉,吴立春,舒小红. 基于分形理论的挟沙水流掺混长度分析[J].人民黄河,2009,31(9):32-33. Ni Zhihui,Wu Lichun,Shu XiaoHong.The mixed length of the sediment-laden flow based on fractal theory [J].Yellow River,2009,31(9): 32-33. [14] 严冰.粉沙质海岸泥沙运动及航道淤积机理研究[D].天津:天津大学,2008. Yan Bing.Study of Sediment Transport and Channel Siltation on Silty Coast [D].Tianjin:Tianjin University,2008. [15] Chien N,Wan Z H.Mechanics of Sediment Transport [M].Reston: ASCE Press,1999. [16] 严冰,张庆河.基于有限掺混长度概念的悬沙浓度垂线分布研究[J].泥沙研究,2008(1):9-16. Yan Bing,Zhang Qinghe.Distribution of vertical suspended sediment concentration based on the finite mixing length conception [J].Journal of Sediment Research, 2008(1): 9-16.2 研究方法
3 验证与比较
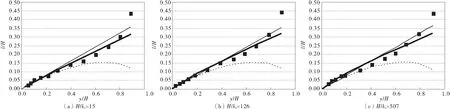
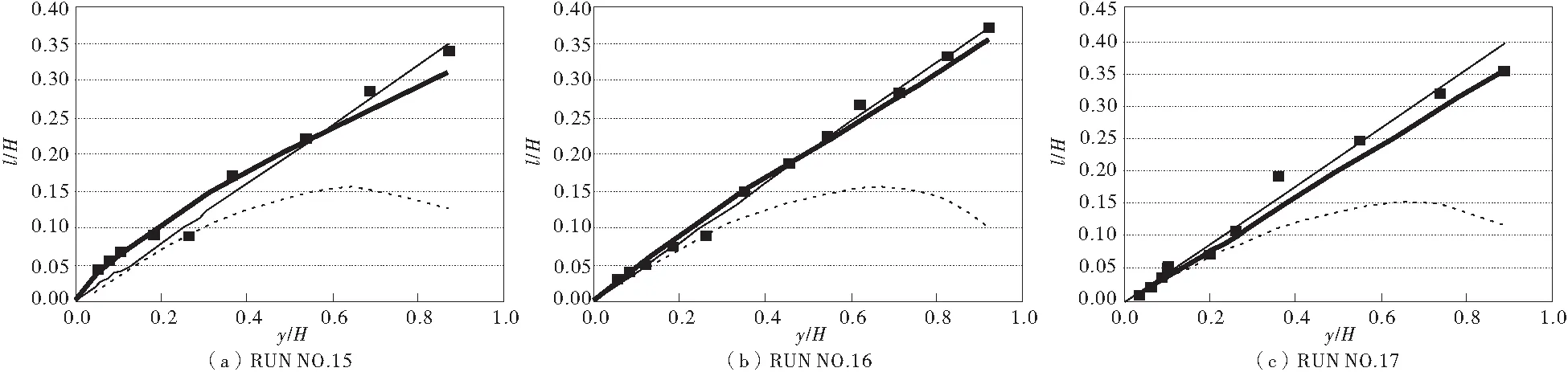
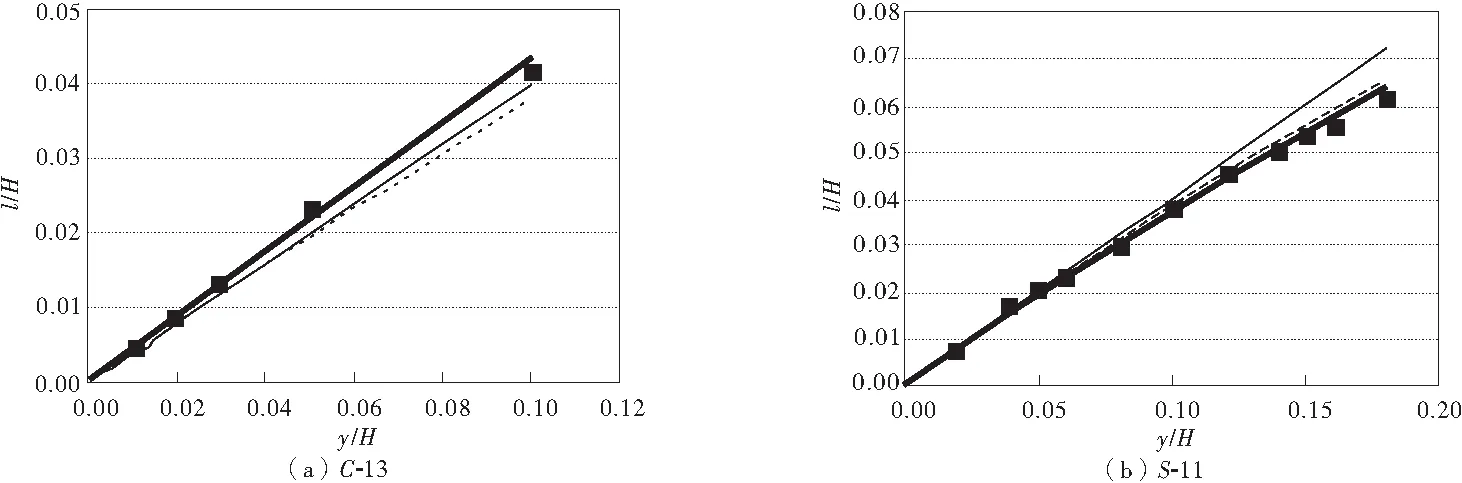

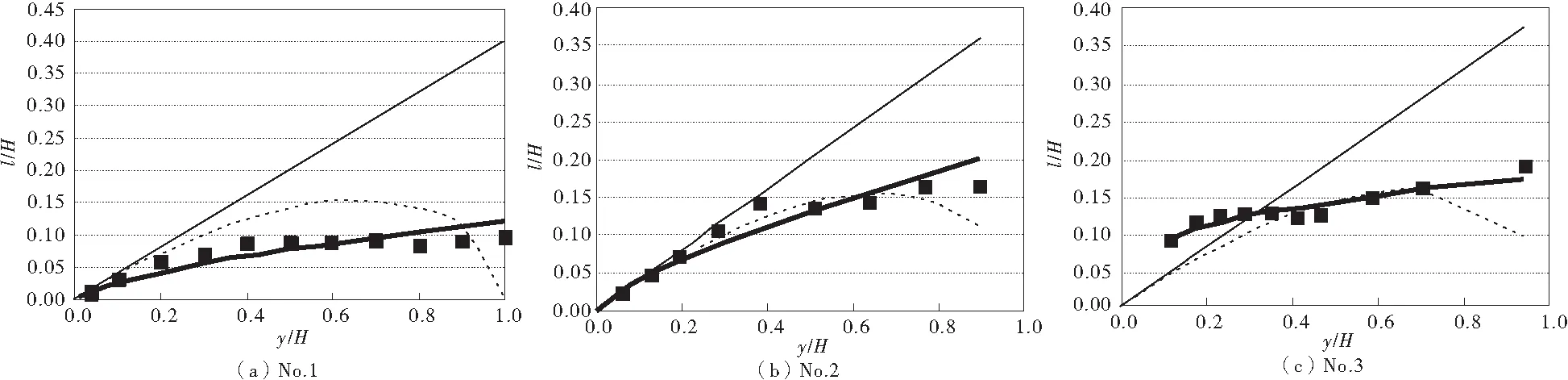
4 初步分析
4.1 分形维数的大小


4.2 分形维数与含沙量的关系

5 结 论

