并联运动模拟平台的运动学分析

郑伟杰，涂群章，潘 明，张晓辰，冯 霞

（解放军理工大学野战工程学院，江苏 南京 210007）

并联运动模拟平台的运动学分析

郑伟杰，涂群章，潘 明，张晓辰，冯 霞

（解放军理工大学野战工程学院，江苏 南京 210007）

为获得某并联六自由度运动模拟平台的运动特性，以该平台的支链为研究对象，建立了各构件的坐标系，在此基础上通过上下平台间的矢量关系和转换矩阵实现平台的位置反解，构建其运动学模型，最后运用MATLAB对构造的运动学模型进行仿真，获得支链长度、伸长速度、伸长加速度的变化曲线。

并联运动；位置反解；运动学

六自由度运动平台由于刚度大、承载能力强、结构简单、运动负荷小等特点，能实现包括仰俯、横滚、升降等多个自由度运动，被广泛应用于机械装备、工程机器人等运动模拟。目前几乎所有六自由度运动平台都采用Stewart结构形式，它主要由上运动平台、下平台底座、上下铰联接装置、液压支链组成。支链与上下平台之间的铰接采用二自由度的虎克铰联接。为更好地开展机械装备的运动模拟，本文对某并联六自由度运动模拟平台进行了运动分析，以该平台的支链为研究对象，通过建立各构件坐标系，利用上下平台间的矢量关系和旋转变换矩阵实现该平台的位置反解，再通过运动学建模，运用MATLAB对构造的运动学模型进行仿真，获得支链长度、伸长速度、伸长加速度的变化曲线，取得了较好的效果。

1 机构铰支点坐标的确定

某并联六自由度运动平台的运动简图如图1所示，可由5个重要参数来表示：上铰圆半径Ra、下铰圆半径Rb、平台处于工作零位时动平台与底座之间的距离H、动平台各相近铰点之间的最短距离Sa（动平台各铰点短边距离）和底座各相近铰点之间的最短距离Sb（底座各铰点短边距离）。另外，l代表支链长度，坐标系XpYpZp和XbYbZb分别代表该平台动坐标系和静坐标系。

如图2所示，分别用矩阵A来表示动平台铰点Ai（i=1，2，3，4，5，6）在动坐标系中的坐标向量。用矩阵B来表示静平台铰点Bi（i=1，2，3，4，5，6）在静坐标系中的坐标向量。矩阵A第一列的第一行至第三行元素分别表示A1点在动坐标系中的Xp轴、Yp轴和Zp轴的坐标，其余列的意义与第一列的意义类似。

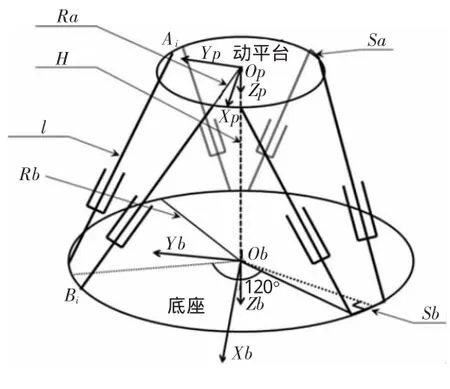
图1 六自由度运动平台结构简图

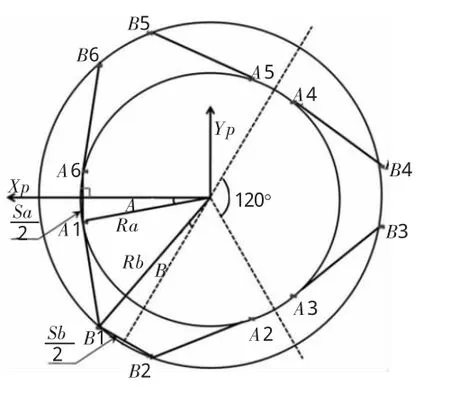
图2 上下平台各铰点的分布

预先定义角度：

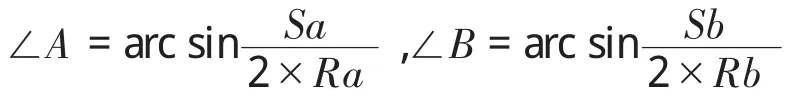
式中，Sa 为动平台各铰点 A6A1、A2A3、A4A5之间的距离；Sb 为底座各铰点 B1B2、B3B4、B5B6之间的距离，则有（s=sin，c=cos）：

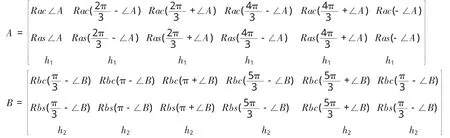
初始位置时，矩阵A在两个坐标系的值完全一致，当平台运动时，A在动坐标系的值不变，但在静坐标系中已发生变化。液压缸活塞杆动平台各铰点在静坐标系的坐标向量用矩阵G来表示，设动平台位姿 Q=q1，q2，…，q6，其中，q1、q2、q3分别表示动平台绕XpYpZp转动的倾角，q4、q5、q6分别表示动平台沿XpYpZp方向的位移量，则由底座到动坐标系的转换矩阵R可表示为：

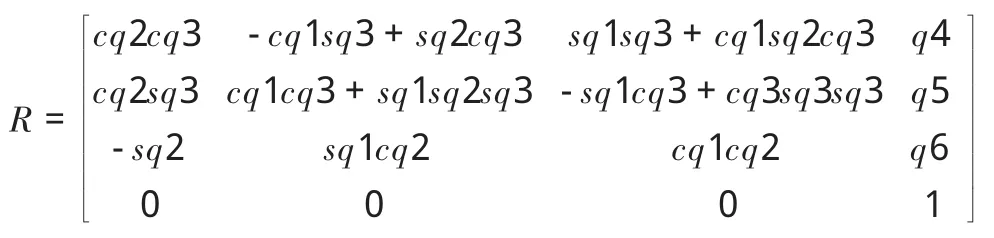
得动平台各铰点在静坐标系的坐标向量G的计算公式为：

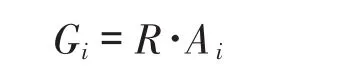
2 平台位置反解

图3为该并联运动模拟平台第条支链的位置分析图，图中Ob为底座平台质心，Op为动平台质心。

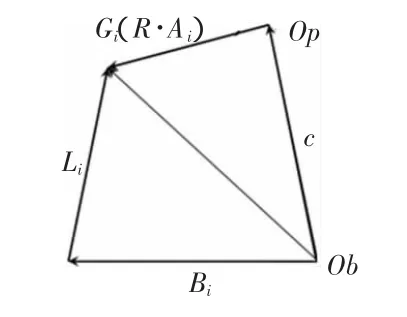
图3 位置分析图

图中，Li表示第i条支链在静坐标系中的位置矢量；c为动平台质心在静坐标系中的矢量，从底座铰链点Bi到动平台的铰链点Ai的矢量为：

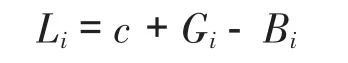
得到第i条支链的长度li：

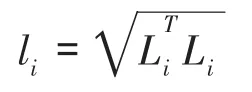
液压缸活塞杆的伸缩量(即位移)可由液压缸的上下铰支点之间的距离减去液压缸活塞杆初始长l0来确定。

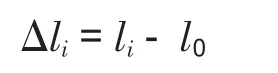
由此可由动平台质心的运动反解得各液压支链的伸长量，即实现平台的位置反解。同样，用动坐标系与静坐标系之间的转换矩阵可以很方便的把平台质心速度和加速度与各铰点的速度和加速度的关系联系起来。

3 速度分析

定义动平台质心在静坐标系中的速度为：

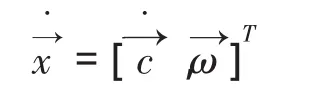
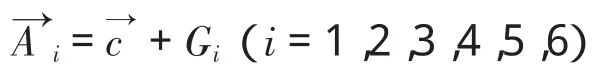
Ai表示A的第i列向量，对上式求导可得到平台各铰点在静坐标系中的速度为：

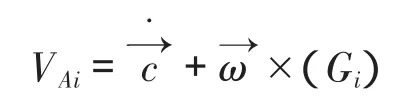
将动平台各铰点Ai的速度矢量VAi相对应的液压支链方向投影即得液压缸伸长速度，式中ni为各液压缸的单位方向向量。

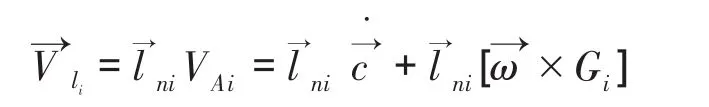
4 加速度分析

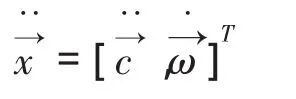
同理，再对动平台各铰点在静坐标系中的速度VAi求导可得动平台各铰点在静坐标系中的加速度：

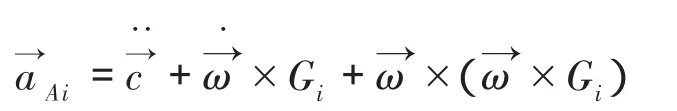
将动平台各铰点Ai的加速度矢量Ai向相对应的液压支链方向投影即得液压缸伸长加速度：

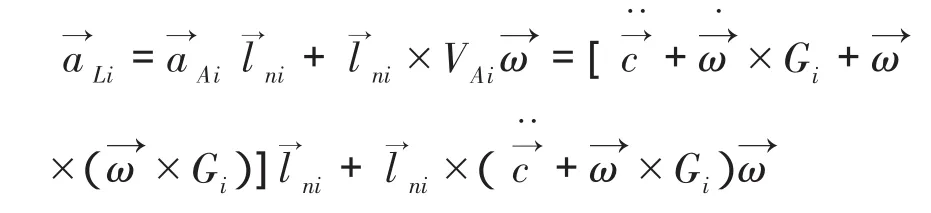
5 运动学仿真与分析

该运动模拟平台主要机械结构参数为：动平台上铰圆半径Ra=1 600mm；底座下铰圆半径Rb=2 000mm；动平台铰点间短边距离Sa=500mm；底座铰点间短边距离Sb=800mm；动平台与底座初始间距H=3 500mm。结合上文的平台位置反解，速度、加速度分析所建立的数学模型，利用MATLAB软件对该运动平台的两种工况进行仿真运算，首先，动平台在t=0～10 s做XpYp平面内的圆周运动x=300sin（πt/10），y=300cos（πt/10），获得平台各支链伸长量变化曲线、速度曲线、加速度曲线分别见如图4～图6所示。

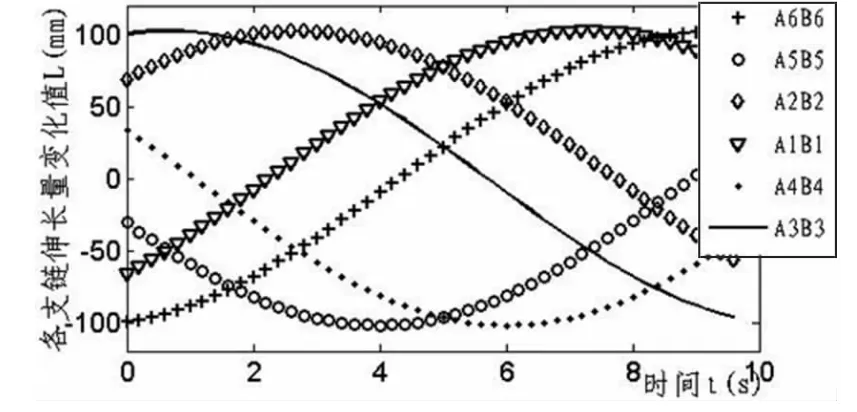
图4 动平台作平面内圆周运动时支链伸长量变化曲线

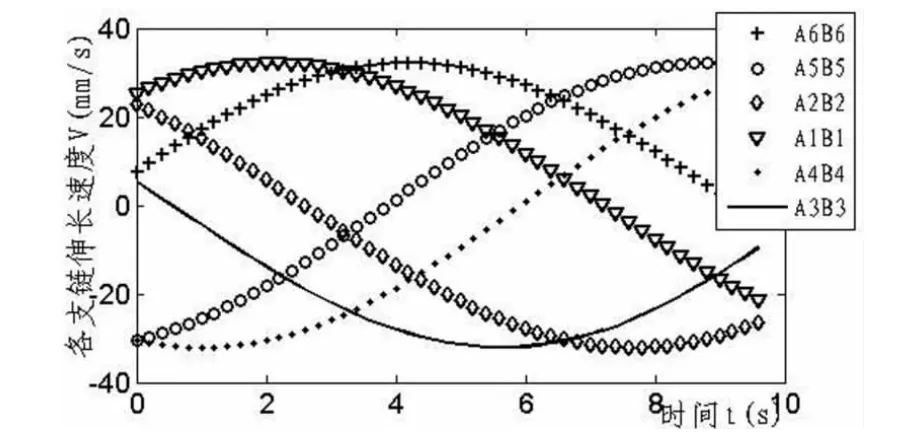
图5 动平台作平面内圆周运动时支链伸长速度曲线

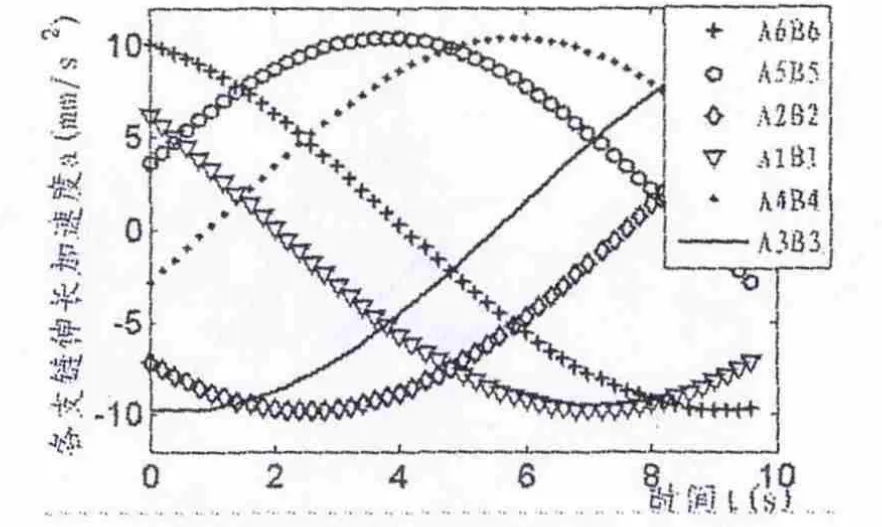
图6 动平台作平面内圆周运动时支链伸长加速度变化曲线

接着，待平台在x=0，y=-300处完全停止后，令平台t=10～20 s内绕X轴做倾角为π/6×（πt/10）的转动，得到平台各支链伸长量变化曲线、速度曲线、加速度曲线分别见如图7～图9所示。

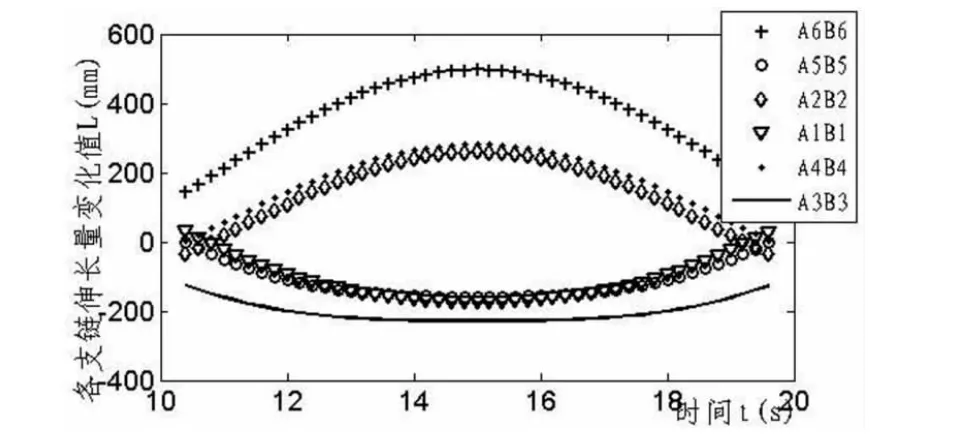
图7 动平台作绕X轴转动时支链伸长量变化曲线

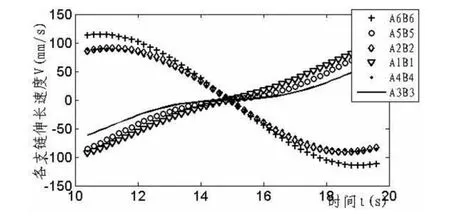
图8 动平台作绕X轴转动时支链伸长速度变化曲线

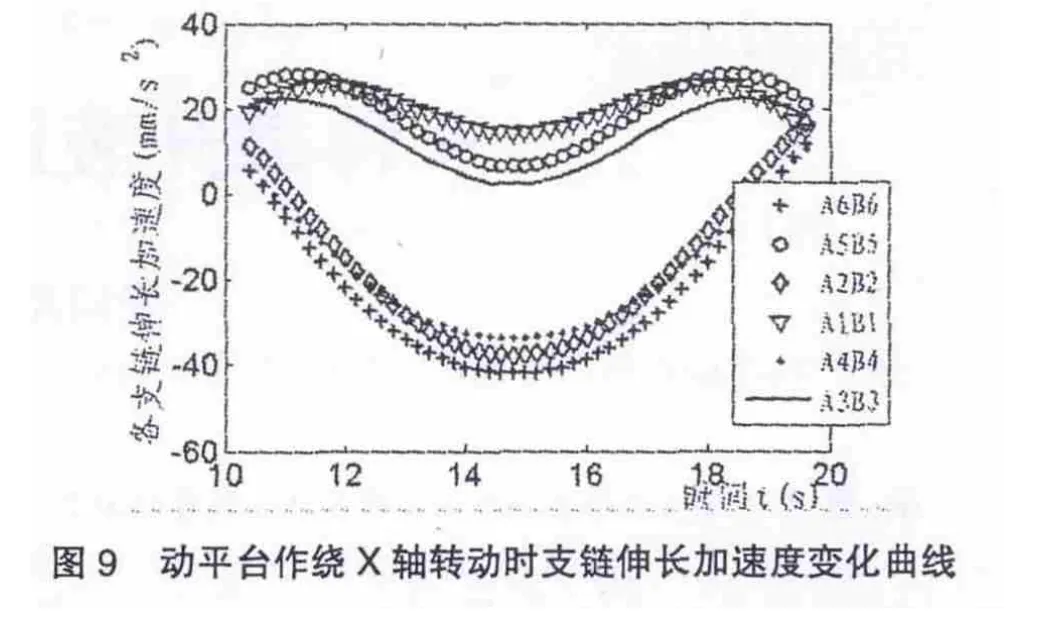
分析图4～图9可知，运动平台在两种工况下，支链伸长量变化曲线、速度曲线、加速度曲线均连续平滑，不存在明显的震荡突变，表明该平台能够在完成各类空间运动等工况中运行平稳，各支链相互间可实现协调的配合，平台机械结构参数较为理想，具有良好的运动性能，便于之后实现精确控制，符合机械装备的一般设计原则。

6 结束语

（1）以并联运动模拟平台的单根支链为研究对象，建立了各构件的坐标系，并通过各构件间的矢量关系，完成了平台的位置反解。

（2）利用动坐标系与静坐标系之间的坐标转换矩阵描述了各支链的运动状态与动平台运动状态间的关系，应用MATLAB对各支链的运动特性进行了仿真分析，得到了每条支链的运动量变化规律，为进一步对并联运动模拟平台进行运动控制设计奠定了基础。

[1]Fichter E F.A Stewartplatform basedmanipulator:general theory and practical construction[J].The International Journal of Robotics Research，1986，5(2):157-182.

[2]Wang Hao,CHEN Genliang,LIN Zhongqin.Foeward Dynamics Analysisof the 6-PUSMechanism Based on Platform-legs Composite Simulation[J].Chinese JournalofMechanical Engineering,2009，22(4):496-504.

[3]扬宏兵，高荣慧，李 兵.六自由度并联机器人的运动学分析与仿真[J].机床与液压，2003(3):133-135.

[4]李 庆，莫孜中，祁力群.非线性方程组的数值解法[M].北京：科学出版社,1999.

[5]薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术及应用[M].北京：清华大学出版社，2002.

[6]郭祖华.6-UPS型并联机构的刚体动力学模型[J].机械工程学报，2002(11):53-56.

Kinematics Analysis ofa ParallelMotion Simulation Platform

ZHENGWei-jie，TUQun-zhang,PANMing，ZHANGXiao-chen，FENGXia
(College of Field Engineering，PLA University of Science and Technology，Nanjing 210007，China)

To directly analyze the kinematic performance ofa six degree of freedom parallelmotion simulation platform,we have now studied its chain,and the coordinate system of components has been set up.Thus the reverse solution of this platform can be proposed on the basis of the vector relation and the transition matrix between the upper platform and the lower platform.Then the kinematic model is constructed,finally,the simulation and calculation of the constructed kinematic model are conducted by MATLAB and the curves of the changing of the chains’elongation,velocity and acceleration of the elongation are obtained.

parallelmotion；reverse solution；kinematics

TH113.2

A

1672-545X（2014）04-0013-03

2014-01-09

郑伟杰（1990—），男，浙江浦江人，在读研究生，研究方向为机电控制。