基于潜艇磁偶极子模型的航空磁探潜探测宽度模型与仿真
杨日杰,熊雄,郭新奇,韩建辉
(1.海军航空工程学院 电子信息工程系,山东 烟台264001;2.海军航空工程学院 指挥系,山东 烟台264001)
0 引言
航空磁探仪由于具有不受传播介质特性的影响、可连续搜索、分类能力好、定位精度高、不受浅海复杂环境影响等优点,成为一种有效的反潜探测设备,在航空反潜中得到广泛应用。相对于声纳探测,航空磁探潜对于声隐身性能良好的潜艇的检测方面更具有其独特的优势,已成为各国竞相研究的重点,然而在国内对航空反潜磁探磁异常探测系统的研究才刚刚起步[1]。
对于反潜探测系统来说,作用距离是一项关键的战术技术指标。自从各种声和非声探测系统问世起,国内外众多学者和研究人员对其各项技术参数进行了广泛而深入的研究,提出了各种探测系统的作用距离模型[2-5]。但航空反潜磁异常探测系统尚未建立有效可靠的探测宽度模型。由于航空磁异常探潜系统被动工作并且随着搭载飞机平台运动,因此影响其探测宽度的因素不仅仅是设备检测能力,还受到环境噪声条件、目标特性和地磁环境的影响。文献[6]通过分析特定的磁偶极子信号提出基于半宽原则的静止磁性物质探测宽度。文献[7]通过计算目标平均磁矩进而估算得到探测宽度。文献[8]基于战术探测距离和三角几何关系得到探测宽度。文献[9 -10]根据经验公式得到磁探仪的探测宽度。很显然实际环境条件下这些方法往往只能粗略的估算航空磁探仪的探测宽度,与真实的航空磁探仪探测宽度有较大差距,特别是这些经验模型不能分析目标磁特性的变化、环境噪声磁噪声等级的变化以及平台特性对航空磁探仪探测宽度的影响。
本文在航空磁探仪经典探测宽度模型的基础上,引入了概率分布的思想,提出基于目标信噪比检测依据的航空磁探测探测宽度计算模型。在航空磁探潜过程中,目标可以等效为磁偶极子模型[11],首先基于目标磁偶极子模型和航空磁探潜的探测过程,建立航空磁探潜的探测模型;其次根据潜艇目标的磁特性和潜艇在地磁环境运动过程中磁特性的变化建立潜艇磁特性模型;再次根据磁探仪的工作原理建立环境噪声条件下磁探仪的检测模型。综合探测模型、目标特性模型、噪声模型和检测模型得到一定信噪比条件下检测概率,进而代入基于目标信噪比检测依据的探测宽度模型即可得到航空磁探潜探测宽度。该探测宽度模型建立和计算过程中,首次综合考虑磁探仪搭载平台的探测方式、潜艇磁目标特性和环境磁噪声特性对探测宽度影响,可以对航空磁探潜过程的磁探仪探测宽度进行有效估计,对航空磁探潜作战使用具有应用参考价值。
1 基于检测依据的探测宽度模型
1.1 经典探测宽度模型
在航空磁探仪设备组合参数中,R 是航空磁探仪设备给定的作用距离,在国内外经典的航空磁探仪探潜的文献[8-10]中,需要进行航空磁探潜探测宽度估计的时候,通常认为R 是定值,则探测宽度随反潜机高度和目标深度的变化而变化,通常描述为如下形式:

式中:R 为磁探仪作用距离指标;H 为反潜机飞行高度;h 为目标深度。
1.2 基于检测依据的探测宽度模型
借鉴搜索论中搜索器材扫描宽度的定义[12],给出基于检测概率对距离积分的探测宽度模型。假设在噪声环境中,航空磁探仪和潜艇目标直线运动相遇于磁性目标和磁探仪相遇过程中,目标与磁探仪航路最近距离点(CPA),航空磁探仪和目标的横向距离为L,检测概率为Pd(L),则航空磁探仪的探测宽度Wmad可以定义为
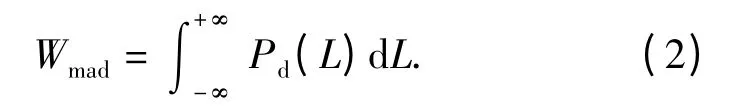
(2)式为目标检测概率在空间的累积,其物理含义表示航空磁探仪的等效平均探测宽度。当按照经典文献[8]中(1)式探测宽度设定,则目标在航空磁探仪的横向距离范围内即被探测到,目标在横向距离范围之外则不被探测到,即检测概率表示为
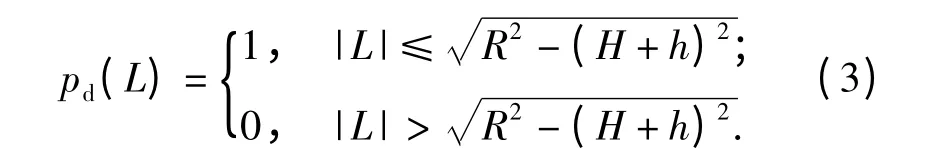
则根据(2)式航空磁探仪的探测宽度为Wmad=此时(2)式就归结为(1)式的特定情况。而实际环境条件下,磁探仪的检测概率并不能简单表示为(3)式的情况,其检测概率不仅受到相对高度的影响而且受到目标特性、环境噪声等级、磁探仪检测方式的影响,因此需要综合各个因素建立精确的计算模型才能得到准确的探测宽度估计。
2 探测宽度模型计算方法
2.1 基于目标偶极子模型的航空磁探潜建模
在航空磁探仪对目标进行搜索和探测的过程中,由于频繁的机动容易产生较高的机动磁异常虚警,因此航空磁探测过程中反潜机一般按照预定的方案保持平稳飞行,可以假设航空磁探仪探测目标的较短时间内,目标和航空磁探仪沿恒定的航向和恒定的航速直线运动。而且航空磁探仪作用距离较小,当目标与航空磁探仪距离较远时,无法探测到目标的磁异常信号,探测到目标磁异常的时刻是在航空磁探仪与目标相近的范围内。因此航空磁探仪探测目标的过程是机动平台探测机动目标的相遇探测过程,为此建立航空磁探仪与目标的相遇探测模型。假设t0时刻航空磁探仪与目标相遇于CPA,则建立如图1航空磁探仪与潜艇相对运动模型。
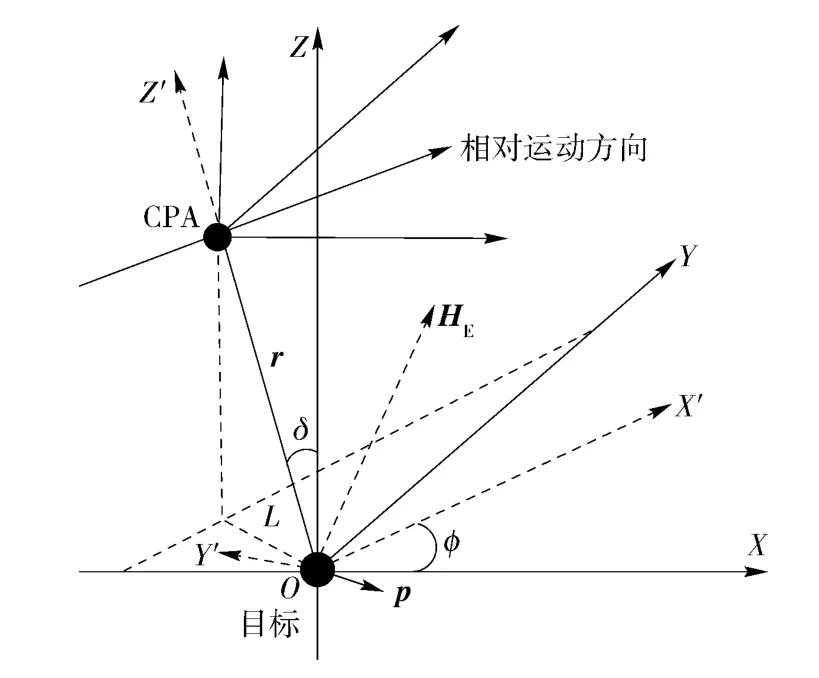
图1 航空磁探仪与潜艇相对运动模型Fig.1 Airborne magnetic anomaly detection encounter model
图1中O 点为目标位置点,OXYZ 为地磁北坐标系,OXY 位于水平面,Y 轴指向磁北方向,X 轴、Y轴、Z 轴相互垂直。OX'Y'Z'为航空磁探仪探潜坐标系。X'轴平行于航空磁探仪相对目标运动方向,Z'轴垂直于X'轴并且指向CPA,Y'轴垂直于OX'Z'平面。由图1可知,OXYZ 坐标系经过两次旋转转换到OX'Y'Z'坐标系。首先沿Z 轴旋转角度φ 到相对航向上,然后沿X 轴旋转角度δ 到CPA.
由于潜艇目标是铁磁性物体,进行航空磁探测时,可以将目标等效为磁偶极子,空气、海水的磁导率近似等于真空中的磁导率μ0,目标在距离r 处产生的磁感应强度B 可以表示为[11]

式中:p 为目标磁矩;r 为目标和探测点之间的距离矢量;μ0=4π×10-7H/m 为真空磁导率。
标量磁探仪测得的信号是目标磁场在地磁场方向上的投影,因为地磁场|HE|≫|B|,则目标磁偶极子场标量磁信号Bmad表示为

假定在相遇过程中CPA 距离为R0,(s,0,R)为航空磁力计在在OX'Y'Z'坐标系中的位置,则目标与航空磁探仪的距离矢量r 在OX'Y'Z'坐标系中可以表示为r=si' +R0k',i'、j'、k'表示OX'Y'Z'坐标系三轴方向的单位矢量。假设l、m、n 为目标磁矩p 在OX'Y'Z'坐标系中的方向余弦,l1、m1、n1为地磁场HE在OX'Y'Z'坐标系中的方向余弦,根据(4)式和(5)式,可以得到OX'Y'Z'坐标系下目标磁信号的表达式:
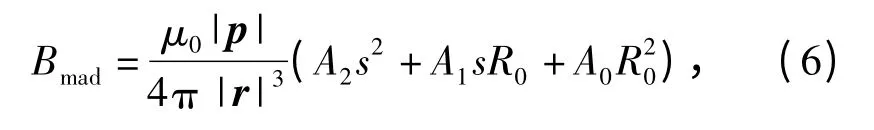
式中:A0=2nn1-ll1-mm1;A1=3(nl1+ln1);A2=2ll1-mm1-nn1.
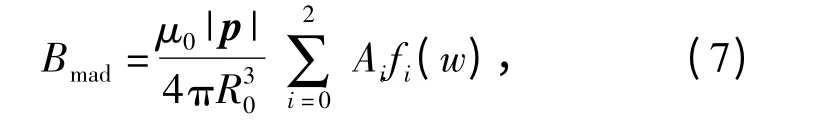
式中:fi(w)=wi/(1 +w2)2.
在OXYZ 坐标系中,假设目标磁矩p 与Z 轴和Y 轴的夹角分别为Ω 和α,则目标磁矩p 在OXYZ坐标系中表示为
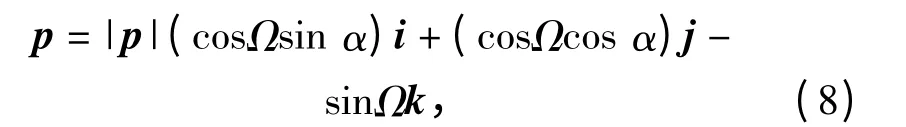
式中:i、j、k 表示OXYZ 坐标系三轴方向的单位矢量。
设地磁倾角为Φ,则在OXYZ 坐标系中

根据坐标转换公式[13],可得到OXYZ 坐标系下的单位向量到OX'Y'Z'坐标系下的单位向量转换:

由(8)式~(10)式可得
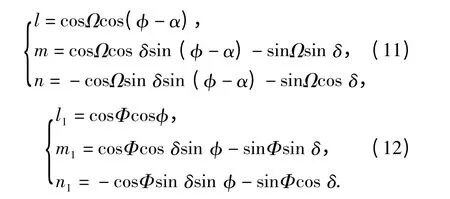
由(11)式、(12)式得到(7)式航空磁探潜磁异常信号模型中系数A0、A1、A2在OXYZ 坐标系下的表示。
2.2 目标磁特性模型
在(7)式航空磁探潜磁异常信号模型中,要求得目标磁异常信号必须对目标的磁矩p 进行估计,但是不同吨位,不同材料特性,以及不同磁航向航行时潜艇的磁特性都将发生变化,因此需要根据这些因素对潜艇目标磁特性进行建模,才能合理估计目标磁特性。

图2 潜艇目标艇体坐标系Fig.2 Submarine coordinate
图2中O 点为目标位置点,OXYZ 为地磁北坐标系,建立磁性目标船体直角坐标系OX″Y″Z″,原点选在潜艇目标中心,Z″垂直向下,X″指向艇首,Y″方向指向右舷。目标的磁航向为沿磁北方向顺时针旋转到达目标航向位置所形成的角度,目标磁航向为β. 设潜艇目标磁矩在地磁北坐标系下由下式表示:
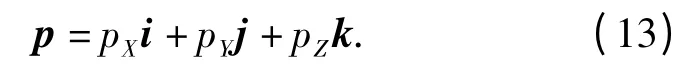
潜艇目标磁偶极子矩在艇体坐标系下表示为
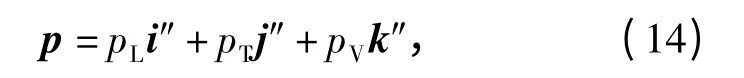
式中:pL、pT、pV分别为沿X″、Y″、Z″方向的磁矩;i″、j″、k″表示OX″Y″Z″坐标系三轴方向的单位矢量。
OXYZ 坐标系经过两次旋转转换到OX″Y″Z″坐标系,首先沿Z 轴顺时针旋转π/2 +β 角度,然后沿Y 轴逆时针旋转180°,根据OXYZ 坐标系地磁场矢量表达式(9)式和坐标转换公式得到地磁场矢量在艇体坐标系下表示为
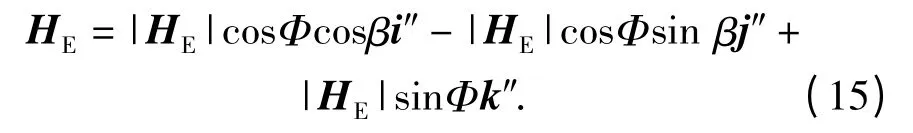
由文献[14]可知,潜艇目标磁场可分为固定磁场和感应磁场,目标的固定磁场与目标的固有特性和消磁水平有关,一段时间之内一般是固定不变的。目标的感应磁矩与潜艇的材料特性和地磁场大小呈正比例关系。设目标3 个轴的导磁因子为fL、fT、fV,目标潜艇的吨位为W,则目标的感应磁系数为kL=fLW,kT=fTW,kV=fVW,目标艇体坐标系三轴的感应磁矩pLI、pTI、pVI为
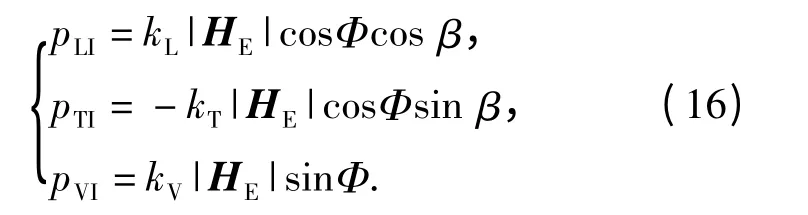
若目标的固定磁矩为pLP、pTP、pVP,则目标在艇体坐标系下3 个坐标轴方向的磁矩为

将目标磁矩pL、pT、pV变换为地磁北坐标系下,OX″Y″Z″坐标系经过两次旋转转换到OXYZ 坐标系,首先沿Z 轴顺时针旋转π/2 +β,然后沿Y 轴逆时针旋转180°,由(16)式、(17)式和坐标转换公式得到OXYZ 坐标系下目标磁矩三分量:

2.3 环境磁噪声及检测模型
在完成飞机平台背景噪声补偿和海洋环境磁噪声等其他噪声处理之后,在航空磁探潜平台平稳飞行的过程中,可以认为剩余噪声是高斯噪声[15],由于经过补偿去平均处理,因此环境磁噪声均值为0,方差为σ2. 在航空磁探测之前都会有一段适应性飞行,可以在适应性飞行过程中进行噪声采样并统计噪声采样的均值和方差,作为计算模型的噪声输入。
航空磁探潜探测方式和探测过程可以得到实际的航空磁探潜检测过程如下:某时刻,将磁力计传感器预处理之后的采样数据作为磁探仪检测器的输入,用于计算检测统计量。若采样窗的长度为2T,采样间隔为2T/M,则采样点为M;若t0时刻航空磁探仪与目标相遇于CPA,则采样间隔[t0-T,t0+T]内的采样信号为B1,B2,…,BM,Bi表示表示磁探仪在ti时刻航空磁探仪采样输出磁信号。若用x 表示检测统计量,x*为检测统计量检测阈值,则当x≥x*表示存在信号,否则不存在信号。因此检测过程是一个双择假设检验模型,可以根据具体型号内置的磁探仪检测算法给定检测统计量和检测阈值。在本文中,由于在探测过程未知目标信息,且未知具体磁探仪设备的检测算法,可以采用最基本的平方律检测算法,采用平方律检测准则计算其检测统计量x,则

由于噪声为高斯白噪声,当没有磁异常信号存在时,x/σ2是M 自由度的卡方分布。根据卡方分布累积分布函数,则在虚警概率Pf条件下,可根据(20)式反解得到检测阈值x*.

式中:P(x/σ2|M)是M 自由度卡方分布随机变量的累积分布函数;σ2是噪声方差。
在有磁异常信号存在的条件下,x/σ2是M 自由度、非中心参数为的非中心卡方分布,则根据(20)式解得检测阈x*,进而可计算出检测概率
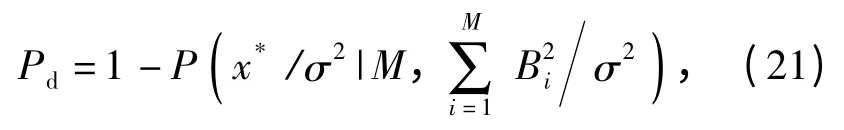
2.4 探测宽度模型计算的基本步骤
基于航空磁探潜探测模型、目标磁特性模型、环境噪声和检测模型可以给出本文提出的基于目标信噪比检测依据的探测宽度模型求解方法,其基本步骤如下:
1)设定目标吨位、目标导磁系数、目标磁航向角、目标固定磁矩、地磁场倾角以及地磁场大小等参数,由(18)式可以估计得到OXYZ 坐标系下的目标磁矩。
2)根据估计的目标磁矩、反潜机航向、反潜机飞行高度、目标深度、反潜机速度和估计目标速度、由(7)式计算不同横距条件下航空磁探潜磁异常信号的采样Bi.
3)根据环境噪声预采样,统计环境噪声等级得到环境噪声方差σ2.
4)设定虚警概率,根据噪声方差和采样窗的长度,由(20)式计算得到检测阈值x*.
5)根据检测阈值,磁异常信号Bi,环境噪声方差σ2,由(21)式计算得到不同横距条件下的检测概率Pd(L).
6)根据计算得到的不同横距条件下检测概率Pd(L),由(2)式即可计算得到设定环境条件下的航空磁探潜探测宽度。
变换不同参数的设定值,即可分析不同条件下相关影响因素对航空磁探潜探测宽度的影响。通常在实际探测中未知目标信息,只需估计目标未知参数在某个区间均匀分布,逐步计算区间上不同参数条件下的探测宽度,进而求平均即可得到未知目标参数条件下的探测宽度。
3 仿真结果及分析
3.1 仿真1:反潜机航向、目标航向对探测宽度影响
仿真参数设定:地磁场为50 035.05 nT,地磁倾角为45°;根据文献[12]可以得到潜艇目标典型的纵向、横向和垂向的导磁系数为7.3 Oe·cm3/(γ·t)、1.6 Oe·cm3/(γ·t)、1.6 Oe·cm3/(γ·t),设定潜艇排水量为6 000 t,航速8 kn,航行深度100 m,由于随着潜艇磁隐身技术的发展,现代潜艇在执行任务前通常进行过消磁,对于消磁后不久的舰船,固定磁矩相对感应磁矩来说,幅值很小,可以近似设定为0;反潜机速度360 km/h,高度100 m,磁航向为90°;磁探仪采样频率为20 Hz,积分时间为20 s,虚警概率为3 次/h;磁噪声方差为0.2 nT;根据2.4 节探测宽度模型计算基本步骤,仿真得到反潜机探测航向为45°、120°、240°、300°时,潜艇以不同磁航向航行时的探测宽度变化曲线,如图3所示。
仿真结果表明:目标磁航向在90°和270°左右时探测宽度存在明显的下降趋势,这是因为该探测模型考虑了地磁场对目标磁特性的影响,在目标磁航向为90°和270°时为东西航向,东向航向上目标的感应磁场大小明显下降,从而导致探测宽度下降。而经典的探测宽度模型是无法反映这种变化趋势的。在相同潜艇航向条件下,随着反潜机探测航向的变化,探测宽度也有变化,特别是潜艇目标航向180°时,变化较为明显。
3.2 仿真2:反潜机高度、目标航向对探测宽度影响
仿真参数设定同仿真1,反潜机探测航向为90°,反潜机高度分别为100 m、200 m、300 m、400 m条件下,潜艇以不同磁航向航行时探测宽度变化曲线如图4所示。
仿真结果表明:随着反潜机高度的增加探测宽度急剧下降,这是因为目标磁场与距离的3 次方近似呈正比,本文的探测宽度模型中充分考虑了目标磁场的这一变化特性,因此更加精确地反映了这一变化趋势,而如果采用经典探测宽度模型则会有较大误差。

图3 反潜机航向、目标航向对探测宽度影响Fig.3 Sweep widths in different plane magnetic and target courses
3.3 仿真3:地磁倾角、目标航向对探测宽度影响
基本仿真参数设定同仿真1,反潜机探测航向为90°,磁倾角分别为20°、35°、50°、65°条件下,潜艇以不同磁航向航行时探测宽度变化曲线如图5所示。
仿真结果表明:随着磁倾角的减小,探测宽度随之下降的,这表示相同地磁场大小的条件下低纬度地区探测宽度要比高纬度地区探测宽度大。在低纬度地区,潜艇沿磁北方向和磁南方向航行时,探测宽度基本相同,随着纬度的增加,潜艇沿磁北航向时探测宽度明显大于潜艇沿磁南航向时的探测度。经典探测宽度模型也无法体现这些特性差异。
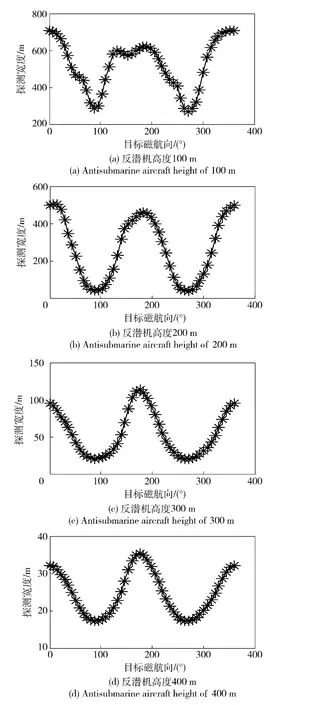
图4 反潜机高度、目标航向对探测宽度影响Fig.4 Sweep widths at different plane height and in different targetmagnetic course
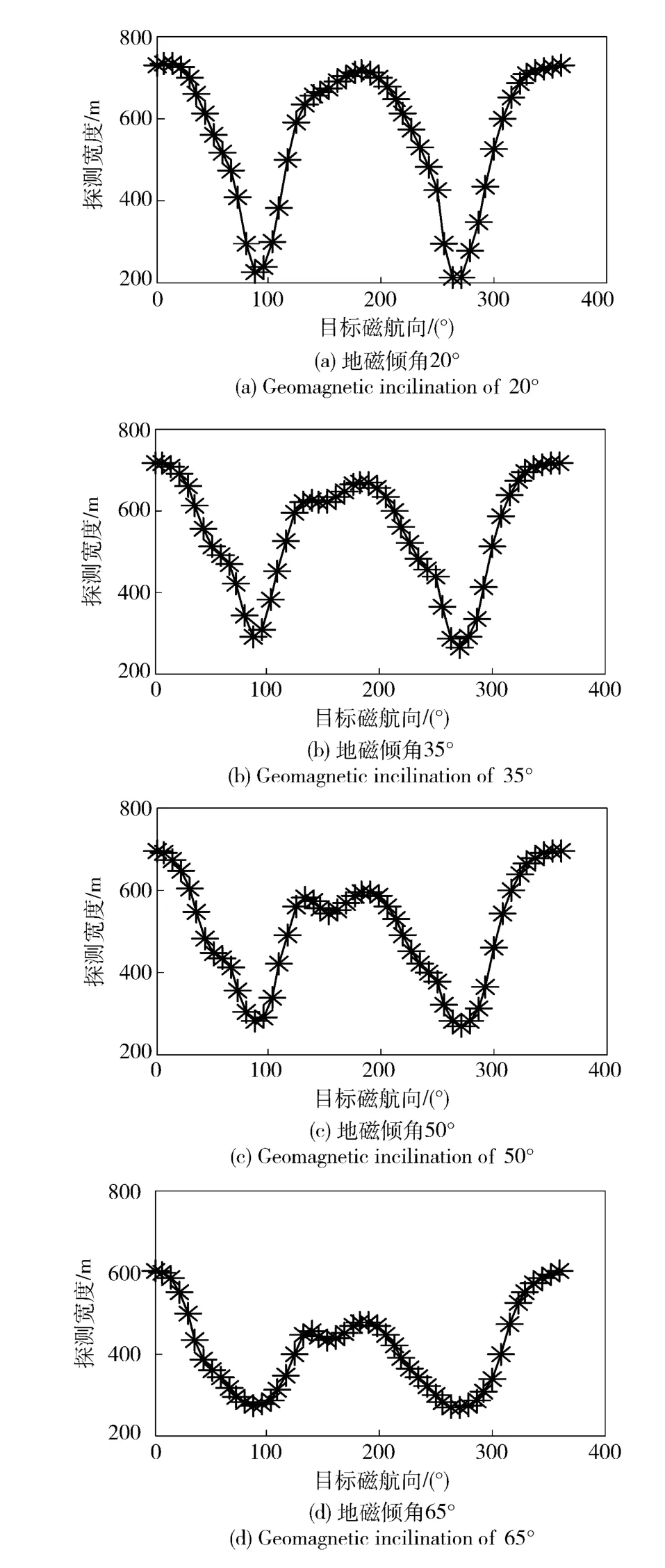
图5 地磁倾角、目标航向对探测宽度影响Fig.5 Sweep widths at different magnetic dip angle and in different target magnetic course
3.4 仿真4:背景磁噪声等级、目标航向对探测宽度影响
基本仿真参数设定同仿真1,反潜机探测航向为90°,环境磁噪声标准差分别为0.1 nT、0.5 nT、1.0 nT、5.0 nT 条件下,潜艇以不同磁航向航行时探测宽度变化曲线如图6所示。
仿真结果表明:随着磁噪声等级的增加探测宽度急剧下降,当磁噪声等级达到1.0 nT 之后,磁探仪探测宽度下降到几十米。航空磁探潜过程中,各种环境磁噪声较为复杂,磁探仪很容易产生虚警,在进行航空磁探测之前必须对环境磁噪声等级进行分析和特性统计才能合理发挥磁探潜优势。

图6 磁噪声等级、目标航向对探测宽度影响Fig.6 Sweep widths under different magnetic noise level and in different target magnetic course
4 结论
本文提出了基于信噪比检测依据的航空磁探潜探测宽度模型,在目标磁偶极子模型基础上,结合航空磁探潜探测模型、目标磁特性模型、环境噪声磁噪声模型以及信噪比检测模型,给出了探测宽度模型求解方法和步骤。分析了航空磁探潜条件下目标特性和环境噪声等因素对航空磁探潜探测宽度的影响,并对其规律进行了总结。本文提出的航空磁探潜探测宽度模型可为航空磁探仪作战使用提供参考。
References)
[1] Peter V C,Alexander R P,Brian R W,et al. Magnetic detection and tracking of military vehicles[R]. San Diego:Quantum Magnetics Inc,2002:1 -4.
[2] 牟达,王建立,陈涛. 凝视型红外搜索跟踪系统对武装直升机作用距离的分析[J]. 兵工学报,2008,29(3):313 -317 MU Da,WANG Jian-li,CHEN Tao. Analysis on operating range of a staring infrared search and track system for armed helicopter[J]. Acta Armamentarii,2008,29(3):313 -317. (in Chinese)
[3] 贾庆莲,乔彦峰,邓文渊. 周视搜索系统对点目标的作用距离分析[J]. 光学学报,2009,29(4):937 -942.JIA Qing-lian,QIAO Yan-feng,DENG Wen-yuan. Analysis for point-target detection range of panoramic searching system[J].Acta Optical Sinica,2009,29(4):937 -942. (in Chinese)
[4] 赵妙娟,车宏. 军用光电系统作用距离分析. 红外与激光工程[J]. 2008,37(增刊):501 -503.ZHAO Miao-juan,CHE Hong. Analysis of the efficient distance of O-E system for military[J]. Infrared and Laser Engineering,2008,37(Supplement):501 -503. (in Chinese)
[5] 李凡,郭圣明,王鲁军,等. 一种新的声纳作用距离指标评估方法[J]. 声学技术,2009,28(3):235 -239.LI Fan,GUO Sheng-ming,WANG Lu-jun,et al. A new approach to prediction of sonar detection range index[J]. Technical Acoustics,2009,28(3):235 -239. (in Chinese)
[6] 边刚,刘雁春,裴文斌,等. 海洋工程中磁性物质探测时探测间距和探测深度的确定[J]. 海洋技术,2008,27(2):41 -45.BIAN Gang,LIU Yan-chun,PEI Wen-Bin,et al. Determination of spacing and depth of detecting lines in magnetic substance detection in marine engineering[J]. Ocean Technology,2008,27(2):41 -45. (in Chinese)
[7] 姚俊杰,孙毅,边少锋,等. 水下磁目标探测线间距确定方法[J]. 海洋测绘,2005,25(4):29 -31.YAO Jun-jie,SUN Yi,BIAN Shao-feng ,et al. The method of defining survey lines space in marine magnetic detection of underwater object[J]. Hydrographic surveying and Charting,2005,25(4):29 -31. (in Chinese)
[8] 蒋志忠,杨日杰,张林琳,等. 基于先验目标分布的磁探仪应召搜潜最佳搜索半径研究[J]. 兵工学报,2011,32(9):1100 -1105.JIANG Zhi-zhong,YANG Ri-jie,ZHANG Lin-lin,et al. Study on optimal circle search radius of magnetic anomaly detector on call based on priori target distribution[J]. Acta Armamentarii,2011,32(9):1100 -1105. (in Chinese)
[9] Phillip C,Pardue A. Computer simulation of a MAD buoy field[R]. Monterey California:Naval Postgraduate School,1990.
[10] 屈也频. 反潜巡逻飞机搜潜辅助决策系统建模与仿真研究[D]. 长沙:国防科学技术大学,2008.QU Ye-pin. Research on modeling and simulation for the decision support system of search submarine scheme by antisubmarine warfare patrol aircrafts[D]. Changsha:National University of Defense Technology,2008. (in Chinese)
[11] Sheinker A,Ginzburg B,Salomonski N. Magnetic anomaly detection using high-order crossing method[J]. IEEE Transactions on Geo-science and Remote Sensing,2012,50(4):1095 -1096.
[12] Stone L D. 最优搜索理论[M]. 吴晓峰,译. 北京:海潮出版社,1990:4.Stone L D. Theory of optimal search[M]. WU Xiao-feng,Translated. Beijing:Haichao Press,1990:4. (in Chinese)
[13] 周宏仁,敬忠良,王培德. 机动目标跟踪[M]. 北京:国防工业出版社,1991:80 -82.ZHOU Hong-ren,JING Zhong-liang,WANG Pei-de. Tracking of maneuvering targets[M]. Beijing:National Defense Industry Press,1991:80 -82. (in Chinese)
[14] PSR. Magnetic signatures of submarines,PSR report 2474[R].Warminster PA:Pacific-Sierra Research for the Naval Air Warfare Center,1994.
[15] Kierstead D P. Computing the mean and variance of time remaining after detection[R]. Stennis:Naval Research Laboratory,1999.

