锥头圆柱体高速入水空泡深闭合数值模拟研究

马庆鹏，魏英杰，王聪，曹伟，陈超倩

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨150001)

0 引言

运动体以一定初速度从空气中穿越气、水交界面进入水中并在其运动轨迹上产生一个狭长空穴这一过程称为入水过程，其后的空穴称之为入水空泡。早在19世纪末，Worthington 等［1］便利用高速闪光照相机、玻璃水槽等设备开展了钢制球体垂直入水的小型实验，对球体入水空泡发展规律开展了研究，阐述了球体入水各个阶段的流动现象。此后的一个多世纪以来，由于入水问题在诸多领域的广泛应用，尤其是诸如空投鱼雷、入水射弹等入水武器方面的应用，入水问题的研究取得了较大的进展。

入水过程可以分为6 个阶段［2］:冲击阶段、流动形成阶段、空泡敞开阶段、空泡闭合阶段、空泡溃灭阶段以及完全沾湿阶段。其中，空泡闭合阶段又分为面闭合和深闭合。面闭合是由于表面喷溅在大气压力、大气密度、空泡口空气流动等多种因素的共同作用下迅速向中间收缩，从而形成一个类似于凸起的钟罩形状的封闭面;深闭合是指空泡排开水体径向扩张动能降为0 后在流体静压作用下向轴向收缩并最终收缩于空泡轴线上一点这一流动现象。空泡闭合尤其是深闭合是导致空泡溃灭的主要原因。

对于空泡闭合的研究多通过实验完成，研究对象多为球体、锥体、圆盘等结构体。美国海军军械实验室的Gilbarg 等［3］通过实验研究了大气压力对球体入水喷溅和空泡的影响规律。May 等［4-6］针对球体、锥体、圆盘等多种形状结构体，开展了大量的低速入水实验，得到了低速入水空泡的发展过程及环境条件对空泡面闭合的影响规律，并分析了入水各阶段结构受到的流体动力。

20世纪后期，学者对入水问题的研究多集中在入水拍击阶段，通过理论分析及数值计算的方法对拍击载荷及喷溅的初始形态开展了大量研究。文献［7］采用边界元法求解了二维楔形体的入水拍击问题，得到了喷溅射流的形态发展规律及楔体表面压力系数。文献［8］针对非对称二维楔形体入水拍击过程开展了理论研究，分析了拍击过程水面喷溅的发展规律。文献［9］采用边界元法求解了三维锥体垂直、倾斜条件下的入水拍击问题，得到了不同拍击状态水面喷溅的形态。

以上研究主要针对入水空泡的发展机理及入水初级阶段的载荷、喷溅形态及面闭合等问题，对于空泡深闭合的研究较少。此外，目前对于入水问题的研究大多为低速条件下，对于高速条件下(大于150 m/s)的实验及理论研究，Lundstrom［10］在美国军方支持下开展了12.7 ～14.5 mm 穿甲弹在805 ～1 070 m/s 速度范围内的入水实验，并提出了一种基于能量守恒的空泡形态预测方法。Lee 等［11］在此基础上提出了空泡深闭合的理论分析方法，对初始速度为500 ～1 500 m/s 的球体入水空泡发展过程开展了相关研究，并与数值模拟结果进行了比较。

21世纪以来，计算机技术的发展使得计算流体力学(CFD)方法得到了更多的应用。王聪等［12］、何春涛等［13］针对小型结构体低速(10 ～50 m/s)入水问题开展了全过程数值模拟研究，分析了入水空泡发展规律，并研究了空气域压强对入水空泡面闭合的影响规律。

本文基于有限体积法和流体体积(VOF)多相流模型，求解了雷诺平均的N-S 方程，考虑入水过程的空化及湍流现象，针对入水过程的深闭合问题，对半锥角为45°的锥头圆柱体以500/s 初始速度自由垂直入水过程开展了数值模拟研究。主要分析了入水空泡形态发展及深闭合现象。得到了深闭合发生的时间及深闭合前后流场的流动特性及压力分布变化特性。

1 数学模型

1.1 流体控制方程

本文数值计算采用VOF 多相流模型描述水、气、汽形成的多相流动，同时假设流体为不可压缩，忽略入水过程中由于流体粘性产生的热效应，建立了该问题的流体控制方程。其中，水相、气相及水蒸汽相的体积分数分别用αl、αg、αv表示，三者满足关系式:

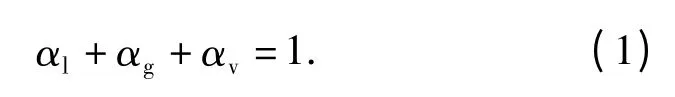
混合介质的连续性方程为

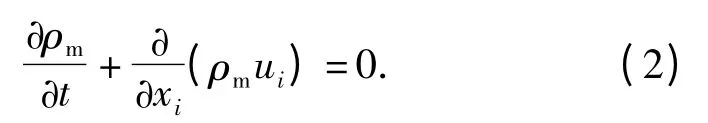
动量守恒方程为

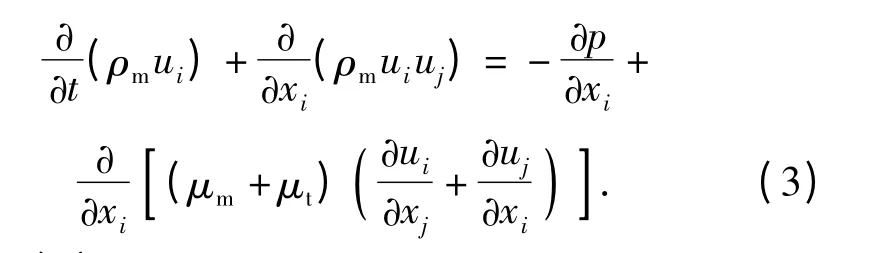
(2)式和(3)式中:ui为速度分量;ρm和μm分别为混合介质的密度和动力粘度;μt=ρmCμk2/ε 为湍流动力粘度。ρm和μm表达式分别为

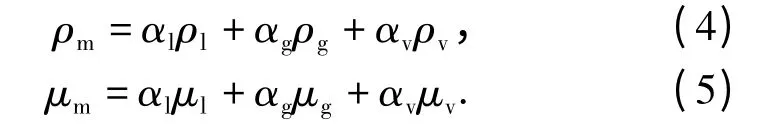
对于入水过程的空化问题，本文采用Schnerr-Sauer 空化模型进行求解，该模型的守恒方程基于水蒸汽相建立，水蒸汽相体积分数的输运方程为

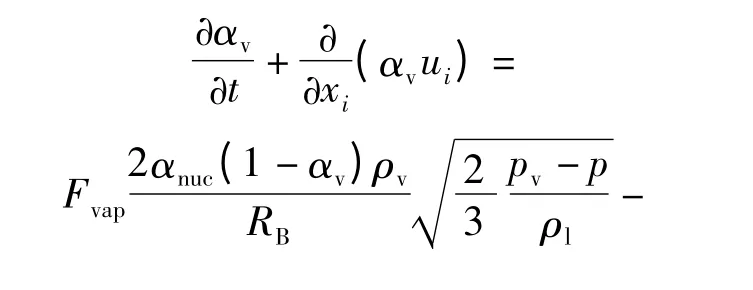
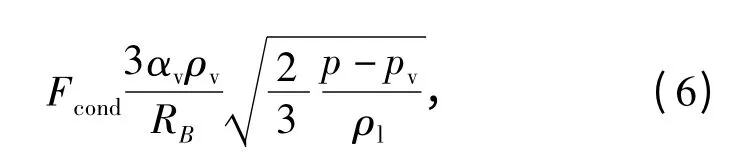
式中:RB=1×10-6m 为气核半径;αnuc=5×10-4为不可凝结气体体积分数;Fvap= 50 和Fcond=0.001为经验常数。

1.2 湍流模型

运动体高速入水过程具有强瞬时、非定常、高载荷等特性，伴随着湍流、相变等复杂的流动过程。对于这一强非线性流动，本文采用k-ω SST 湍流模型进行计算。k-ω SST 模型由Menter［14］提出，它综合了k-ω 模型近壁稳定性和k-ε 模型边界层外部独立性的优点。

2 数值计算

2.1 计算模型及网格划分

本文计算的运动体外形、尺寸以及计算域二维示意图如图1所示。运动体为锥头圆柱体，柱段直径D=10 mm，柱段长度L =5D，锥头半锥角为45°.计算域为圆柱形，为排除壁面边界对中心流场影响，取计算域直径Dd=100D. 计算域长度为230D，其中自由液面上方空气域长度为32D，水域长度198D，运动体锥头顶端在初始状态下距自由液面2D 处。

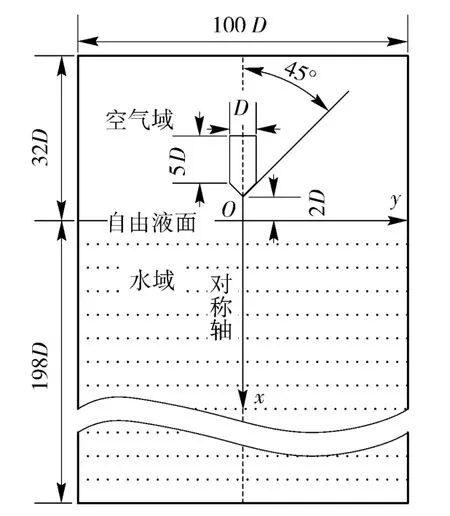
图1 运动体及计算域示意图Fig.1 Sketch of projectile and computational domain

考虑到运动体及计算域几何形状都为轴对称体，本文采用二维轴对称模型开展数值模拟研究。流域网格划分及边界条件设置如图2所示。为保证空气域、汽水交界面以及空泡区域计算结果精度，对计算区域网格进行了局部加密处理。运动体周围，轴向前后2D、径向6D 范围计算域采用三角形网格加密，其余为四边形网格，运动体表面第一层网格厚度为D/400，加密区与外部过渡网格厚度为D/20.运动体上方沿x 轴负向网格高度为D/20 均布，前场沿x 轴正向渐疏，初始网格数量为275 768.

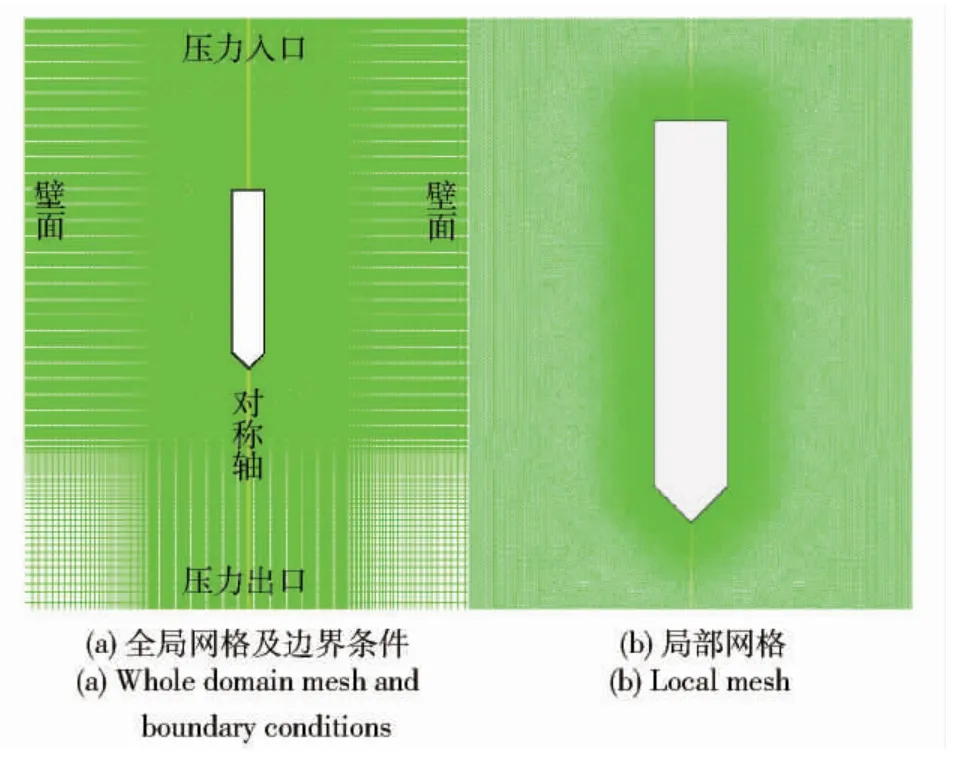
图2 计算网格示意图Fig.2 Sketch of the mesh

2.2 数值方法

本文采用有限体积法对流体控制方程离散，采用PISO 算法对压力-速度场的耦合进行求解;压力场的空间离散采用PRESTO!格式;各相体积率离散采用CICSAM 格式;综合考虑收敛性与计算时间，对动量方程的离散采用一阶迎风格式。

计算中引入UDF 自编程实现运动体沿x 轴正向运动，并采用动网格技术定义网格运动和更新。动网格更新方法采用动态层法，网格更新过程中，为保证空气域计算精度，新生成网格高度均为D/20.

3 计算结果与分析

3.1 空泡深闭合预测模型

文献［11］在文献［10］的基础上提出了一种预测入水空泡形态的理论分析模型，入水空泡发展过程如图3所示。

假设流体不可压缩，忽略入水过程热交换产生的能量损失及重力影响，由能量守恒原理可知，运动体动能损失等于排开水的动能和空泡的压力势能之和。在此基础上，忽略运动体尺度，文献［11］给出了空泡半径的预测公式:

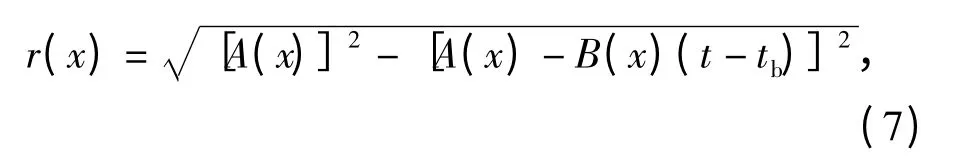
式中:t≥tb，t 为运动体当前位置时刻，tb为x =xb时刻;A(x)和B(x)分别为

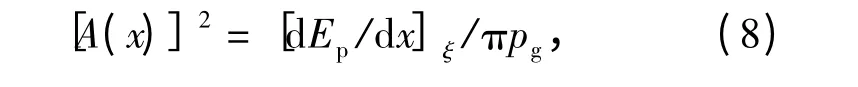
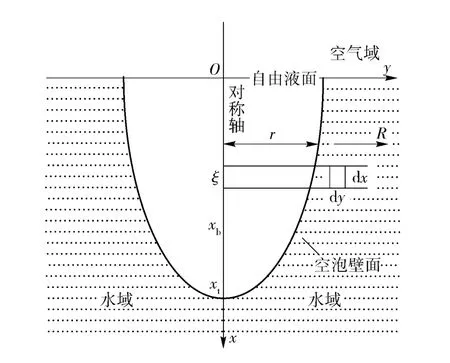
图3 入水空泡示意图Fig.3 Illustration of water entry cavity

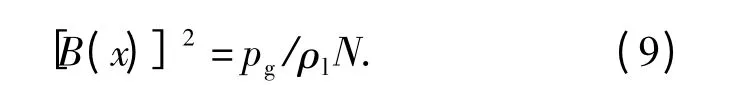
(8)式、(9)式中:Ep= mv2p/2 为运动体动能;pg=px-pc，px为该深度绝对压强，pc为空泡内部压强，本文取pc为饱和蒸汽压强3 540 Pa;N=ln(R/r)，R为扰动流场半径，r 为空泡半径，本文取R/r =30.此外，对于本文模型，需在(7)式右侧加上运动体半径r0=D/2.

(7)式的求解依赖于运动体各时刻的速度与位移数据，对于该运动，由牛顿第二定律可得

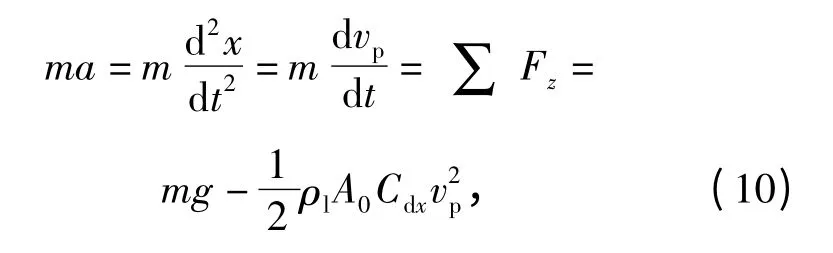
式中:A0为运动体特征面积;vp为瞬时速度;Cdx=Cd0+σ 为运动体阻力系数(其中空化数σ=2(p∞-pc)/(ρlv2p)，p∞为远场压力)，对于半锥角45°的圆锥头，σ=0 时的阻力系数Cd0=0.498［2］;g 为重力加速度。因此，(10)式可改写为

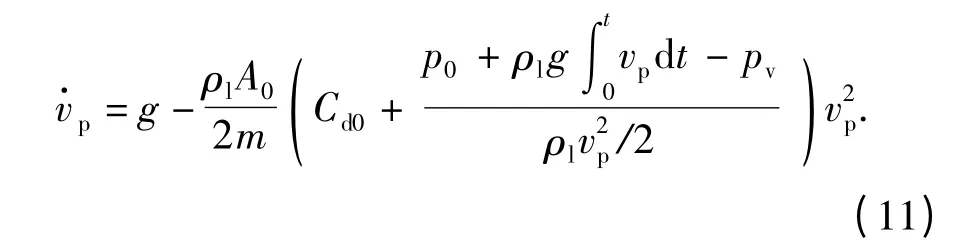
给定边界条件vp|t=0=500 m/s，求解(11)式，便可得到任意时刻运动体的速度及位移，代入到(7)式中便可得到给定时刻下任意xb≤xt位置的空泡半径。

令(7)式右侧等于0，可得在xb位置空泡半径为0 的两个时刻:

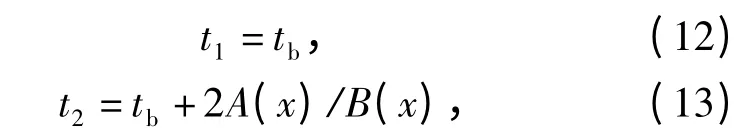
式中:t1为初始时刻，td=t2即为空泡在该点闭合的时刻。

由(8)式、(9)式可知，对于给定的tb，A(xb)、B(xb)皆为固定值，因此由式(13)可以求得在空泡长度范围内，任意深度下空泡闭合所需时间，而空泡发生深闭合位置即为xd= x(min(tb)).

3.2 入水弹道

对前文描述的半锥角45°锥头圆柱体以500 m/s初始速度自由垂直入水问题进行数值模拟，得到了入水过程中运动体速度vp及入水深度x/D 随入水时间t 的变化。另一方面，由(11)式可以得出理论分析结果，两种结果对比如图4所示。

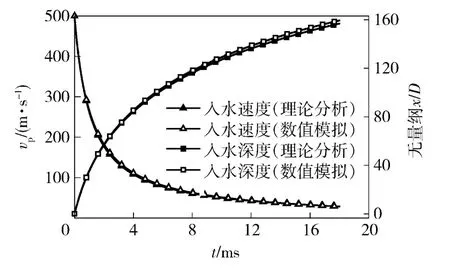
图4 数值模拟与理论分析结果对比Fig.4 Comparison of thenumerical results and analytical results

由图4可以看出，对于运动体速度衰减曲线，两种方法得到的结果基本一致，在入水初期及曲线后半段吻合度极高，在中段稍有区别，数值模拟结果稍微偏大。这一区别在位移曲线上得到了体现，可以看出，从速度值差别稍大的时间点开始，位移值也开始出现偏差，由于积分累加的缘故，在18 ms 处，两种位移计算结果差别最大。这一差别主要由于两种方法基于求解不同的方程，且理论分析模型忽略了空泡面闭合对运动体运动的影响，因此，对于本文高速条件下入水问题，这一误差值是可以接受的。

3.3 入水空泡

3.3.1 空泡形态

图5给出了理论求解与数值模拟在入水深度x/D 为30D 时空泡形态结果对比。从图5可以看出，两种方法得到的空泡外形在自由液面以下吻合较好，由于理论分析模型未考虑液面喷溅，因此水面以上区别较大。同时，对于理论分析模型中不同的N=ln(R/r)取值，空泡半径有一定的差异。

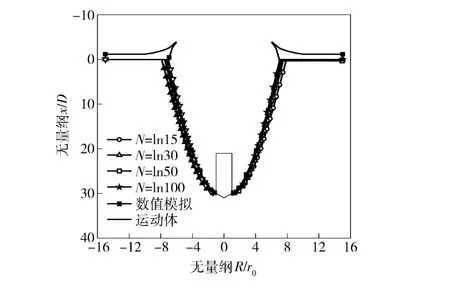
图5 入水深度30D 位置空泡形态对比Fig.5 Comparison of the cavity shapes at thepenetration depth H=30D

图6给出了入水空泡的发展过程云图，可以看出，在整个入水过程中，空泡经历了形成、面闭合、扩张、收缩、深闭合、溃灭等几个阶段。在入水后1.0 ms左右，空泡发生面闭合现象，入水喷溅逐渐增厚并向空泡内部侵入;在5.0 ms 后，最大空泡直径无明显增大，空泡在面闭合以及流体静压的共同作用下开始向对称轴收缩，并在大约16.5 ms 左右深闭合;随后空泡被纵向拉断，水体迅速向两端压缩，空泡迅速溃灭。

3.3.2 空泡深闭合流场分析

为确定本文计算模型的深闭合位置，对空泡收缩段的流场进行了分析。

1)深闭合区域流线分布

图7给出了空泡收缩段附近流场流线分布图，其中，每一时刻采取二维轴对称显示，竖直向下为重力方向。由图7可以看出，在16.30 ms 时，空泡尚未闭合，此时刻流线显示，该段空泡外流体基本沿垂直空泡壁面方向向轴线运动，在空泡内部，流体向下运动。16.30～16.38 ms 这一过程，空泡壁面逐渐靠近对称轴，空泡附近流动逐渐复杂。随着空泡壁面的收缩，在16.36、16.37 ms 时刻，可看到空泡内部产生少量水滴悬浮在空泡内部，阻碍了空泡内部介质向下运动。随着空泡的继续收缩，空泡内壁与水滴间距逐渐减小，在16.38 ms 时刻时，水滴上方流体无法再向下流动，并与水滴下方介质在水滴位置相会，这导致了空泡内部流动被阻隔，虽然此时空泡内壁尚未与对称轴接触，但是实际上空泡已经发生了深闭合现象。空泡深闭合后，在内部流体交汇处逐渐形成多处涡旋，如16.5 ms 时刻流线图所示。这些涡旋将流场分隔为数段，从图中水滴位置变化可明显看出空泡分离后向上下两端收缩的趋势。

由文献［2］可知，在低速条件下的入水问题中，空泡深闭合往往发生在一点，而本文算例的深闭合位置并非是清晰的一点，而是在一段较长区域里形成数处涡旋导致深闭合，这一现象主要由高速入水特征决定。由于本文研究的运动体直径较小，高速条件下入水过程较长，深闭合深度较深，空泡深闭合时运动体动能损失较大，这就导致深闭合位置附近水体在轴线方向上的速度梯度较小，该区域水体在极小时间内闭合时不易区分。另一方面，由于高速入水空化效应，空泡内部充满水蒸汽、气相及少量水相的混合介质，空泡深闭合时水体与空泡内部混合介质复杂的相互作用对空泡闭合点有较大的影响。

2)深闭合位置结果对比分析

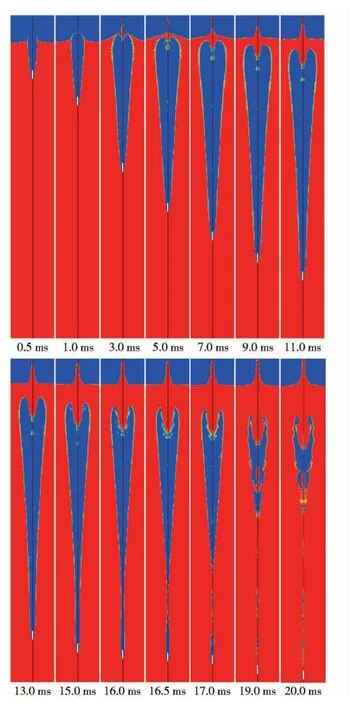
图6 入水空泡发展过程云图Fig.6 Contour of cavity evoluation

上文求得运动体速度、位移数据后，由(8)式、(9)式、(13)式得到空泡发生深闭合的时间td及位置xd，同时，也可得到此时运动体的入水深度xtd.对于不同的N=ln(R/r)取值，上述求解结果也有一定差异，表1给出了数值模拟求解结果以及4 种不同扰动流场半径下的理论分析结果，其中，数值模拟的闭合取闭合段轴向中心点位置。

图7 深闭合位置附近流线分布Fig.7 Streamlines around the deep closure position

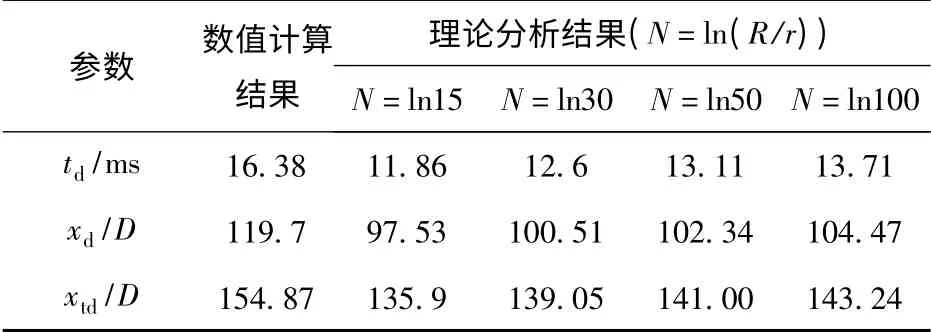
表1 入水空泡深闭合时间及位置表Tab.1 Times and positions of deep closure

由表1可以看出，在N 取值不同，即扰动流场半径R 取值不同时，理论分析结果稍有差异，N 取值越大，与数值模拟结果相对误差越小。其中，对于深闭合位置xd，N 取值递增时，理论分析的4个结果与数值计算结果分别相差18.52%、16.03%、14.50%、12.72%。这表明，理论分析模型在扰动流场半径的选择上对计算结果有一定的影响。其原因一方面是由于理论分析模型简化较多，尤其忽略了面闭合和空泡内部气相的影响，另一方面在于理论分析模型忽略了模型尺寸，其闭合半径相对于数值模拟也相差一个模型半径。

3)深闭合区域压力场分布

图8给出了空泡深闭合前后闭合点附近压力分布云图及水蒸汽相云图。从图8可以看出，在空泡闭合接近前，压力最大值出现在运动体头部位置，空泡内主要由低压的水蒸汽相构成。随着空泡不断收缩，水体挤压水蒸汽相将其排开，并在闭合点附近出现一段高压区。当空泡收缩到一定程度后，周向水体在对称轴上一段区域内闭合，在撞击点处压力达到最大。随后，闭合水体形成两股射流向空泡两端运动，进一步挤压空泡内部混合介质，并在空泡分离点处产生压力极大值。这表明，空泡深闭合过程中，周围水体势能逐渐转化为动能，在与空泡内部混合相作用时产生了较大压力，压力极值作用点随着闭合射流运动而改变直至空泡完全溃灭。

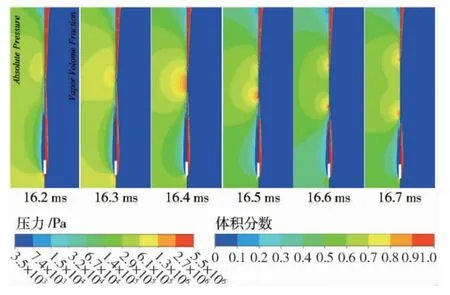
图8 空泡深闭合压力分布及水蒸汽相云图Fig.8 Contour of the pressure field and vapor fraction

4 结论

本文对半锥角为45°的锥头圆柱体以500 m/s的初始速度自由垂直入水问题开展了数值模拟研究，对入水过程的速度、位移以及空泡形态进行了相关分析，结果与文献理论分析模型得到的结果对比吻合较好。同时，研究了入水深闭合的形成过程及流场特性，得到以下结论:

1)小型运动体高速入水深闭合发生在面闭合之后，深闭合时运动体行程较远，闭合位置较深。

2)在空泡内部气、水、水蒸汽混合介质的影响下，高速入水深闭合多发生在一段区域内，且历时极短，深闭合后空泡迅速溃灭。

3)在空泡深闭合区域流场压力值较大，压力极值出现在闭合区域流体撞击位置，随着空泡逐渐分离，高压区始终出现在水体与空泡分离点作用位置。

References)

［1］ Worthington A M，Cole R S. Impact with a liquid surface studied by the aid of instantaneous photography［J］. Philosophical Transactions of the Royal Society，1900，194(A):175 -200.

［2］ May A. Water entry and the cavity-running behavior of missiles，AD A020429［R］. Dayton:ASTIA，1975.

［3］ Gilbarg D，Anderson R A. Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water［J］.Journal of Applied Physics，1948，9(2):127 -139.

［4］ May A，Woodhull J C. Drag coefficients of steel spheres entering water vertically［J］. Journal of Applied Physics，1948，19(12):1109 -1121.

［5］ May A，Woodhull J C. The virtual mass of a sphere entering water vertically［J］. Journal of Applied Physics，1950，21 (12):1285 -1289.

［6］ May A. Effect of surface condition of a sphere on its water-entry cavity［J］. Journal of Applied Physics，1951，22(10):1219 -1222.

［7］ ZHAO R，Faltinsen O. Water entry of two-dimensional bodies［J］. Journal of Fluid Mechanics，1993，246:593 -612.

［8］ Semenov A，Iafrati A. On the nonlinear water entry problem of asymmetric wedges［J］. Journal of Fluid Mechanics，2006，547:231 -256.

［9］ Sun S L，Wu G X. Oblique water entry of a cone by a fully threedimensional nonlinear method［J］. Journal of Fluids and Structures，2013，42:313 -332.

［10］ Lundstrom E A，Fung W K. Fluid dynamic analysis of hydraulic ram Ⅲ，AD 031644［R］. Dayton:ASTIA，1976.

［11］ Lee M，Longoria R G，D E Wilson. Cavity dynamics in highspeed water entry［J］. Physics of Fluids，1997，9(3):540 -550.

［12］ 王聪，何春涛，权晓波，等. 空气压强对垂直入水空泡影响的数值研究［J］. 哈尔滨工业大学学报，2012，44(5):14 -19.WANG Cong，HE Chun-tao，QUAN Xiao-bo，et al. Numerical simulation of the influence of atmospheric pressure on water-cavity formed by cylinder with vertical water-entry［J］. Journal of Harbin Institute of Technology，2012，44(5):14 -19. (in Chinese)

［13］ 何春涛，王聪，闵景新，等. 回转体匀速垂直入水早期空泡数值模拟研究［J］. 工程力学，2012，29(4):237 -243.HE Chun-tao，WANG Cong，MIN Jing-xin，et al. Numerical simulation of early air-cavity of cylinder cone with vertical waterentry［J］. Engineering Mechanics，2012，29(4):237 -243.(in Chinese)

［14］ Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications［J］. AIAA-Journal，1994，32 (8):1598 -1605.