照相站空间基准标定方法及测量误差分析

王唯，唐志华，罗红娥，陈平

(南京理工大学 瞬态物理国家重点实验室，江苏 南京210094)

0 引言

弹道靶道配备的闪光阴影成像系统通过捕捉弹丸飞临瞬间留下的阴影获得弹丸在飞行过程中的空间姿态及位置信息。通过多台阴影成像系统在不同位置获得弹丸的飞行信息，可以确定弹丸在飞行路径上的姿态变化规律并依此计算和评价弹丸的弹道性能与相关指标。而为了能够正确综合各站信息，准确计算弹道参数，需要校准各照相站的空间基准坐标，即确定各个相机的空间位置。目前基于CCD相机的弹道靶道照相成像系统主要有正交阴影成像系统［1］、双目视觉成像系统［2］和三维重构系统［3］等。无论是哪一种成像系统均要求系统中的各个相机满足确定的空间位置关系。考虑到相机镜头与相机之间的装配误差、CCD 感光器件本身的工艺误差以及结构间隙、安装误差等因素，单纯依靠机械结构很难保证系统中的各个相机处于设计要求位置。因此依靠成像系统进行精确测量之前必须进行系统标定。

本文开展了两部分工作:第一，结合前人相关的研究成果简要介绍了成像系统的两步标定方法;第二，在明确相机内、外参数和照相机位置之后，依据阴影成像原理建立了测量误差的数学模型，并在相机位于标定面同侧、至标定面等距以及图像识别误差满足独立同分布的假设前提下，分析了测量误差一次矩、二次矩的空间分布。

1 相机标定

在数字图像处理、计算机视觉和摄影测量领域，对于数字图像的标定、校准和修正已经有了比较深入的研究［4-7］。较为一致的做法是依据小孔成像原理分别建立相机的内参数和外参数矩阵，从而确定物和像之间的关系，然后利用标准模板的数幅图像，通过最优化方法确定内参数，最后计算外参数。尽管在具体的处理方法上存在较多变种，但是应用最为广泛的还是由Zhang［5］最先总结的方法。值得注意的是，Zhang 等的方法可以完全确定从物到像的映射关系，所以可以利用多张图像标定相机，但是并不能通过唯一像来确定物体的空间位置。要通过图像确定物体空间位置需要在物体上建立若干位置关系已知的标志点或从已知的不同方位同时对物体成像。

1.1 内参数标定

首先确定相机镜头的光圈和焦距并进行限位，防止在操作过程中变化。使用相机对标定物［4］进行成像，改变标定物的放置角度以获得同一标定物不同角度的多张图像。进而利用相关算法［5-7］确定内参数和镜头畸变。图1所示为一台相机的内参数标定结果。

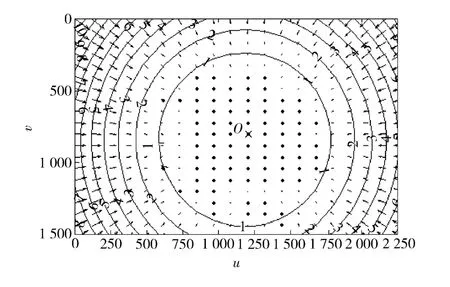
图1 镜头畸变及光轴中心位置Fig.1 Lens distortion and central position of optical axis

1.2 相机外参数标定

基于小孔成像模型和欧拉变换公式，物与像之间的映射关系为

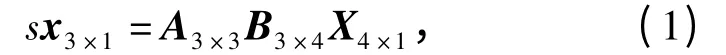
式中:s 是任意比例系数;x3×1=［u v 1］T是增广后的像点坐标，u 和v 分别是像点的像素横坐标和纵坐标(定义在相机图像上，以图像左上角为原点，分别以向右和向下作为横坐标和纵坐标的正向);X4×1=［x y z 1］T是增广后的物点坐标，x、y 和z 分别是空间物点坐标;矩阵A3×3是单应矩阵，可通过内参数标定确定;矩阵B3×4由方向余弦矩阵及平移向量组成，也称相机的外参数矩阵。若令R3×3表示从世界坐标转换到相机坐标的旋转矩阵，t3×1表示世界坐标系中相机的位置坐标，则B3×4表示为

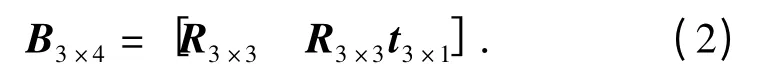
确定内参数矩阵A3×3之后，依据相应的物、像点坐标，利用旋转矩阵的正交性可以确定B3×4.Zhang 在文献［5］中已经做了较为详尽的论述，故本文不再赘述。

2 照相站标定

(1)式通过将物点变换到投影平面，建立了投影平面到像平面的映射关系，从而确定了成像系统中物点与像点之间的关系，其中内参数矩阵主要与镜头相关，在锁定镜头后可视为不变量。照相站标定需进一步确定各个相机之间的位置关系，与外参数矩阵密切相关。为简便起见，以下只讨论世界坐标到对应相机坐标的变换。参考(2)式外参数矩阵的定义，第i 个相机坐标与世界坐标之间满足关系:

式中:x'i为相应相机坐标的点坐标。相机外参数确定的是相机相对标定平面之间的位置关系。由于相机只能获得三维实体在成像平面内的投影，所以通过外参数只能将像点转换为世界坐标中特定平面上的点。若使用Zhang［5］的方法标定相机，则通过该相机所成的图像可以确定物点在标定平面上的投影。当使用多台相机对目标成像时，通过每台相机的图像均可获得物点在标定平面上的投影坐标，而物点的位置则在各相机焦点与对应投影点连线的交点上，如图2所示。

图2 多台相机确定物点坐标Fig.2 Point coordinates determined by cameras

投影点坐标可以通过选取对应图像上的点，依次经过内参数矩阵和外参数矩阵的逆变换得到，其z 坐标恒定为0，表示投影点在标定平面上。Xi=［xiyi0］T(i=1，2)分别表示两个投影点的坐标。而焦点在标定面决定的世界坐标中的坐标可以表示为

由于像点坐标选取误差等因素影响，由相机焦点及对应投影点确定的两直线通常并不相交，故(5)式一般无解，但利用广义逆(Moore-Penrose 广义逆)可获得范数最小意义下物点坐标的最优估计C+［x1y1x2y2］T.

3 误差分析

3.1 误差模型

一般情况下(5)式中的矩阵C 为列满秩，仅当两相机光轴重合(现实中不可能)时矩阵C 的秩才等于2. 所以有

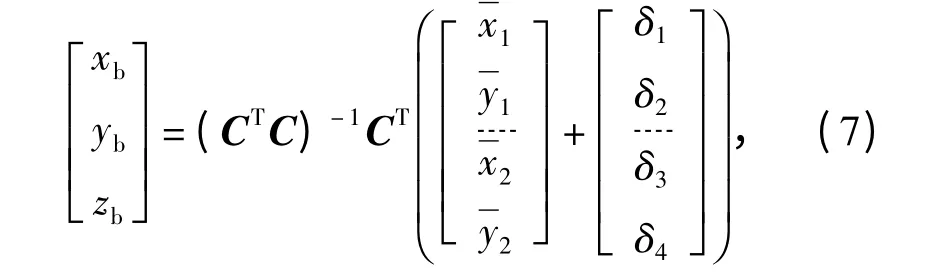
式中:δ1、δ2、δ3和δ4是选取坐标x1、y1、x2和y2时产生的偏差，相应的坐标真值分别表示为和由于投影坐标真值以及必定可以使(5)式存在唯一确定解，所以真值坐标满足关系式:

若将δ1、δ2、δ3及δ4视为独立的随机变量，并假定其概率密度函数相同且均满足由均值μ 和方差σ确定的正态分布(当采用相同的程序选取图像上的点时，该假设是合理的)，于是物点坐标识别偏差的概率特性与随机向量［δ1δ2δ3δ4］T的概率特性之间满足关系:

3.2 偏差的均值

将(9)式代入(10)式，可以发现物点坐标识别偏差的均值由E1和E2组成。

E1=μ［1 1 0］T(由(9)式的第一个矩阵获得)，表示物点坐标中x 和y 方向(见图2)的测量偏差均值与图像上坐标选取过程产生的偏差均值一致，而z 方向(见图2)测量偏差的均值恒定为0，即z方向坐标的测量是无偏的。

E2相对复杂(由(9)式的第二个矩阵获得)，其对物点测量偏差均值的贡献与相机位置、投影坐标真值(即物点的真实位置)有关。图3示出了相机位置分别为(10，200，500)和(200，-1 000，1 000)时，标定面附近x 方向测量偏差的均值系数。

特殊情况下，若假定相机位于标定面同侧，且与标定面等距，即Δz1=Δz2，则向量V1-V2与两投影点真值构成的向量平行，由相似三角形的几何关系，E2可简化为

图3 标定面附近x 方向偏差均值系数Fig.3 Mean coefficient of deviations near calibration surface in direction x

式中:h 表示物点到标定面的距离。(12)式表明Δz1=Δz2时，偏差增益只由物点及相机到标定面的距离确定，而与物点在x 和y 方向(世界坐标)的位置无关。当相机与标定面的距离确定之后，物点在相机前方距相机越近，偏差增益越小。另外，(10)式表明无论在x、y 方向还是z 方向，若图像坐标的选取过程是无偏的，则测量坐标也是无偏的。

3.3 偏差的方差

将(9)式代入(11)式，当Δz1=Δz2时得到偏差的方差为

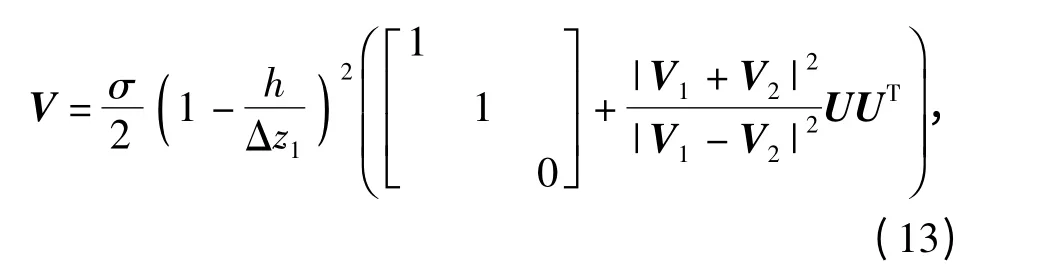
式中:

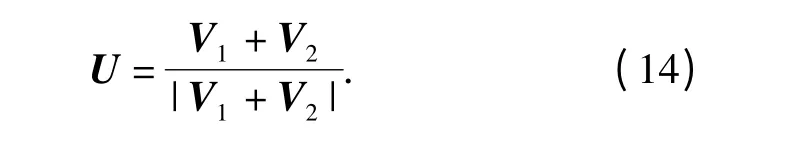
图4示出了相机分别位于(0，1 000，1 000)和(0，-1 000，1 000)时，yz 平面内y 方向测量偏差的自协方差系数由(13)式和图4可知:1)坐标测量值各个分量的偏差不是独立的随机变量;2)物点靠近镜头有利于减小测量偏差的随机分布;3)减小|V1+V2|与|V1- V2|的比值(V1与V2夹角较大时)也有利于减小测量偏差的随机分布。

图4 yz 平面内y 方向偏差自协方差系数Fig.4 Auto-covariance coefficient of deviation on plane yz in direction y

4 结论

基于相机内外参数标定的结果和有关性质，通过对阴影成像系统成像原理的分析，利用泰勒级数对图像坐标拾取偏差引起的空间坐标测量误差进行了研究。选取级数的一阶非耦合项作为误差模型，假定图像坐标拾取误差相互独立且满足相同的正态分布，利用随机向量之间的传递矩阵以及相应的概率传递规律，导出了坐标测量值的均值与方差，并得到以下结论:

1)坐标测量误差的均值和方差均与图像坐标点的拾取误差相关，图像坐标点拾取误差的一次矩和二次矩分别以因子的形式出现在坐标测量误差均值和方差的表达式中。

2)一般情况下坐标测量误差的均值和方差矩阵均与相机、标定面以及物点之间的相对位置相关，且测量误差分量非独立(协方差一般不为0)。

3)当相机位于标定面同侧且与标定面等距时，测量误差的均值仅与物点到标定面的距离相关且呈线性关系;测量误差的方差矩阵则与物点的空间坐标相关且呈现非线性关系。

4)当物点位于标定平面与相机之间且靠近相机时，无论是测量误差的均值还是方差均有减小的趋势。

本文的论述均假设点光源位于镜头焦点(目前已有相应光路予以保证)，并且未对光源偏离焦点引起的误差进行分析。当该假设成立时，依照本方法得到的标定状态对测量误差的影响即由(12)和(13)式(相机位于标定面同侧且等距)描述，或者在更一般的情况下由(10)式和(11)式描述。

本文所述方法可以直接应用于现有照相站的空间基准标定。由于使用求解旋转矩阵的方法来确定相机位置，无需进一步要求相机和标定物之间的相对位置关系。但为了获得较为平坦的测量偏差均值及方差的空间分布，建议约束相机到标定面的距离，使各相机位于标定面同侧且等距。另外，对靶道内多个照相站进行标定时，需要进一步测量或限制标定面的空间位置，从而获得一致的靶道空间基准。

References)

［1］ 顾金良，陈平，夏言，等. 数字式靶道阴影成像系统［J］. 弹道学报，2009，21(4):38 -41.GU Jin-liang，CHEN Ping，XIA Yan，et al. Digital ballistic range shadowgraph system［J］. Journal of Ballistics，2009，21(4):38 -41. (in Chinese)

［2］ 宋晋，马军，蒋敏，等. 双目视觉系统在风洞伞摆角测量中的研究与应用［J］. 计算机测量与控制，2012，20(8):2042-2044.SONG Jin，MA Jun，JIANG Min，et al. Research and application of parachute swing angel in wind tunnel test based on stereo vision measurement system［J］. Computer Measurement ＆ Control，2010，20(8):2042 -2044. (in Chinese)

［3］ 马锁冬，朱日宏，李建欣，等. 瞬态飞行目标三维面形的多视角测量系统［J］. 中国激光，2010，37(12):3091 -3097.MA Suo-dong，ZHU Ri-hong，LI Jian-xin，et al. A multi-view measurement system for three-dimensional surface distribution of transient moving target［J］. Chinese Journal of Lasers，2010，37(12):3091 -3097. (in Chinese)

［4］ Sepp W，Fuchs S. DLR CalLab and CalDe-the DLR camera calibration toolbox［EB/OL］. http:∥www. dlr. de/rm/desktopdefault.aspx/tabid-3925/6084_read-9201.［2013-10-05］.

［5］ Zhang Z Y. A flexible new technique for camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11):1330 -1334.

［6］ Carlos Ricolfe-Viala，Antonio-José Sánchez-Salmerón. Robust metric calibration of non-linear camera lens distortion［J］. Pattern Recognition，2010，43(4):1688 -1699.

［7］ Jean-Yves Bouguet. Complete camera calibration toolbox for Matlab［EB/OL］. http:∥www. vision. caltech. edu/bouguetj/calib_doc/index.html.［2013-10-05］.

［8］ 李竹良，赵宇明. 基于单幅图片的相机完全标定［J］. 计算机工程，2013，39(11):5 -8.LI Zhu-liang，ZHAO Yu-ming. Full calibration of camera based on single image［J］. Computer Engineering，2013，39(11):5 -8. (in Chinese)