抛物线形断面正常水深简化解析式
张丽伟
(齐齐哈尔市河道管理处,黑龙江 齐齐哈尔 161006)
抛物线形断面渠道是水利水电灌排及城市供排水工程中的应用最广泛断面形式之一[1-2]。由于该种断面水力计算涉及繁复的超越方程求解,为了提高计算工作效率及成果精度,相关科研人员已开展了大量卓有成效的研究[3-8],有关研究成果也较好地解决了常规计算方法存在的不足。
由于三次抛物线形断面正常水深计算涉及不可积分函数,且为超越方程,因此,到目前为止,有关抛物线形断面渠道正常水深简化计算方面的研究仅限于在半立方抛物线及二次抛物线形两种断面[9-10]。在实际工程中,由于受地形、地质及过流条件的制约,也因三次抛物线形渠道断面更接近水力最优的U形断面,因此,三次抛物线形渠道也是实际工程常常采用的断面形式之一[11]。
本文利用三次抛物线近似积分法完成了三次抛物线形断面正常水深计算公式中不可积函数的积分求解,进而完成了相关无量纲参数计算,并依据参数关系采用优化拟合的方法[12-15],以标准剩余差最小为目标函数,经逐次逼近拟合,获得了一种较为简捷、适用范围广、计算精度较高的近似解析式,便于实际推广应用。
1 正常水深基本计算公式

式中 Q为过水流量(m3);n′为渠床糙率;i为渠底坡降;A 为过水断面面积(m2);X 为过水湿周(m)。
三次抛物线形断面曲线方程为:

式中 a为抛物线形断面形状参数。以曼宁公式表示明渠均匀流方程为[16]:其过水断面面积及湿周为
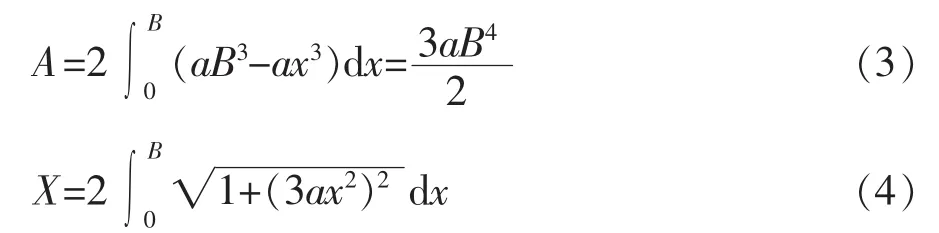
式中 a为抛物线形状参数(m2);B为过水断面水面宽度的 1/2(m)。
在式(4)中,仅当指数n为个别值时(如 n=1.5及2.0)函数可以完成积分,通常情况下均无法通过常规完成积分。为此,采用二次抛物线近似法完成对式(4)的积分,其计算公式为
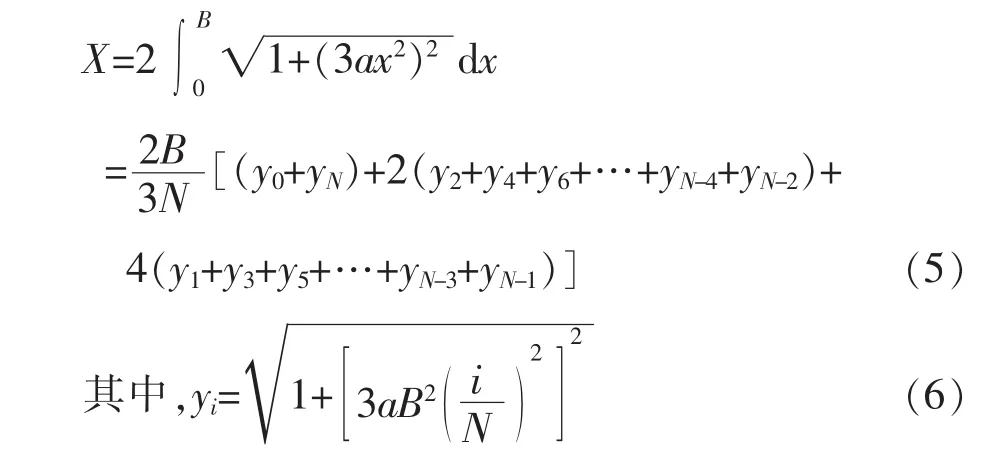
式中 N为在函数自变量x积分区间[0,B]内平均等分的份数(N应为偶数);yi为自变量为第i个等分点时被积分函数的计算值(i=0,1,2,3,…,N)。
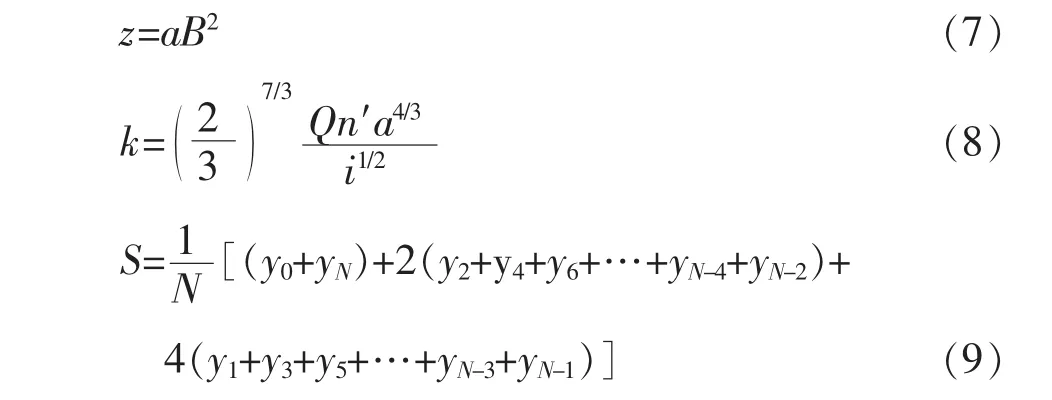
在式(3)、式(5)及式(6)中,设:将式(3)、式(7)~式(9)代入式(1),经进一步整理得:

式中 k为已知综合参数;z、S均为中间变量。
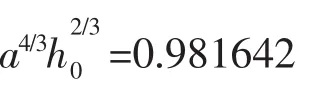
通过设定N值,选取不同的z,即可由式(5)完成积分计算。为有效提高计算精度,在进行N的取值时,将N的每次增加幅度取为6,并将上一次与本次s计算值的相对误差小于0.01%时作为最终N的取值。N值确定后,利用式(10)即根据已知的综合参数k通过试算法求得z,进而由式(11)求得正常水深h0,即:

2 正常水深简化通式的建立及精度分析
2.1 简化通式的建立
因式(10)为超越方程,无法直接获解。为避免利用式(10)求解超越方程问题,现假设 z′=f(k)(z′为 z的近似替代值)函数在工程实用范围内 (即0.15≤z≤6.0,0.0016<k<30.6)可以替代式(10),并满足:①要有较好的拟合替代精度,以确保正常水深的最终计算成果满足工程设计要求;②拟合替代公式的表达形式应最简洁化。
依据式(10)即可通过设定值计算出不同的z所对应的k,并完成关系曲线展绘(如图1所示)。
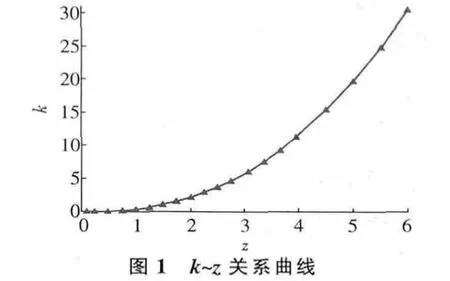
由图1可见,与具有较好的指数关系。在兼顾拟合精度高、表达形式简单两个必备条件下,采用数值拟合分析方法,以标准剩余差最小为目标函数[17-18]即:
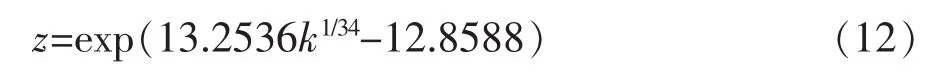
利用式(12)也可不必进行繁复的近似积分计算,直接完成当已知三次抛物线的形状参数a及渠道半水面宽度B情况下渠道的通过流量Q,即为
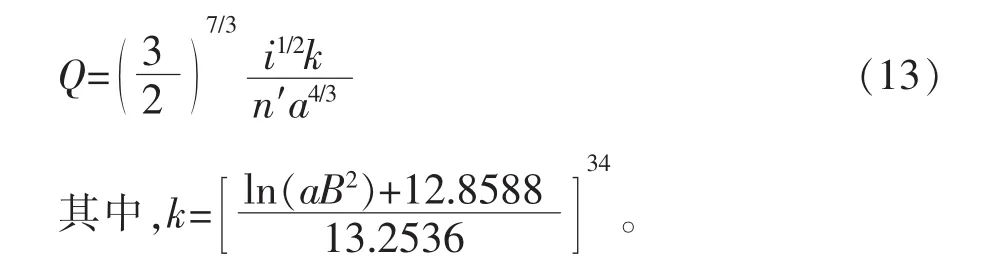
2.2 精度分析及比较
为比较式(12)与式(10)的拟合精度,在工程实用范围内,取不同的 nj、zi(由式(11)可求得 h0ji)即可由式(10)计算出与之相对应的 kji,再将 nj、kji代入式(12)求得与之相对应的z′ji,进而由式(11)求得 h′0ji,并由式(14)完成拟合相对误差计算,如表1所示。
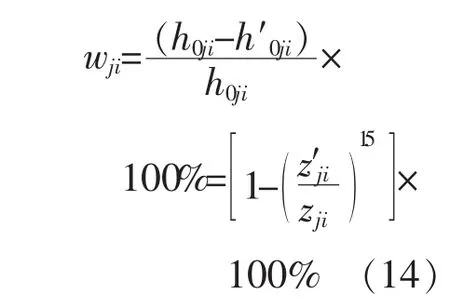
式中 wji为当n取第j个值、z取第i个值时的计算相对误差(%)。
由表1可见,在工程实用参数范围内,用式(12)替代式(10)求解 h0的最大相对误差仅为0.941%。本文式(12)具有较好的拟合替代精度。
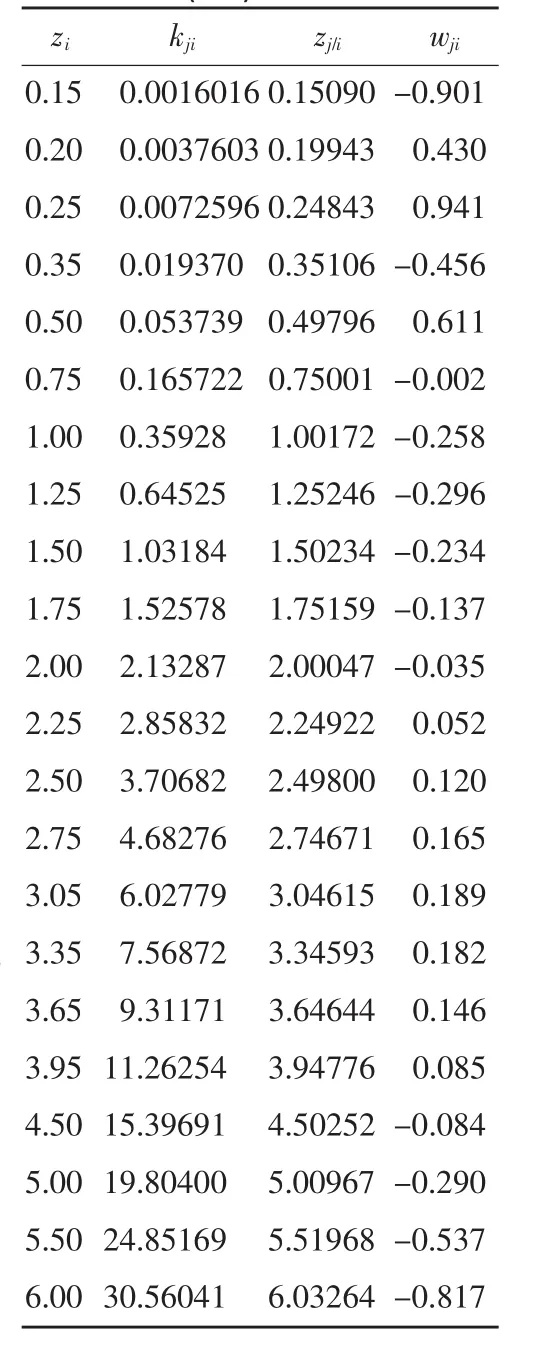
表1 式(12)计算精度比较
3 算例
3.1 算例1
某三次抛物线形渠道横断面的曲线方程为y=0.1x3,渠道糙率 n′=0.025,坡降 i=5.2×10-4,求当过水流量Q=45m3/s时渠道的正常水深h0。
由式(8)可得:k=0.88907,将 k 代入式(12)即可求得:z=1.41771,再由式(11)即可求得该渠道的正常水深为h0=5.338m。利用微机编程求得精确解为h0=5.324m,本文公式计算相对误差为0.26%。
3.2 算例2
如例1中抛物线形渠道横断面的曲线方程不变,求当半水面宽度B分别为4.5m和3.762m时渠道的通过流量Q。
根据已知参数由式(13)可分别求得当B为4.500m和3.762m时,k分别为2.19905和0.88513,则由式(13)可分别求得当B为4.500m和3.762m时,渠道通过的流量Q分别为111.30m3/s和44.82m3/s。
利用微机编程可求得对应上述半水面时渠道通过流量的精确解分别为111.35m3/s和45.0m3/s,本文公式计算成果的相对误差分别为0.045%和0.400%。
4 结语
通过近似积分及优化拟合的方法获得了三次抛物线形渠道断面正常水深的简化计算公式,公式表达形式简单、实用范围广,误差分析及实例计算表明,在工程实用范围内,计算断面正常水深的最大相对误差为0.941%,完全满足实际工程的水力计算及设计精度要求。
[1]魏文礼,杨国丽.立方抛物线渠道水力最优断面的计算[J].武汉大学学报(工学版),2006(3):49-51.
[2]张志昌,刘亚菲,刘松舰.抛物线形渠道水力最优断面的计算[J].西安理工大学学报,2002,18(3):235-237.
[3]文辉,李风玲.立方抛物线断面渠道收缩水深的直接计算方法[J].人民长江,2009,40(13):38,59.
[4]王正中,王羿,赵延风,等.抛物线形断面河渠收缩水深的直接计算公式[J].武汉大学学报(工学版),2011,44(2):175-177,191.
[5]谢成玉,滕凯.三次抛物线形渠道断面收缩水深的简化计算公式[J].南水北调与水利科技,2012,10(1):136-138.
[6]马子普,张根广,赵春龙,等.立方抛物线形渠道水跃共轭水深的迭代算法[J].人民长江,2013,44(1):90-93.
[7]汪曹青,马子普.二次抛物线形渠道临界水深与共轭水深简化算法[J].水电能源科学,2012,30(6):111-113.
[8]冷畅俭,王羿,王正中.抛物线形断面渠道共轭水深的直接计算公式[J].排灌工程机械学报,2013,31(2):132-136.
[9]谢成玉,滕凯.抛物线形断面渠道均匀流水深的近似计算公式[J].水电能源科学,2012,30(7):94-95,172.
[10]滕凯.半立方抛物线形渠道正常水深的近似计算公式[J].长江科学院院报,2012,29(12):30-32.
[11]冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-31,35.
[12]滕凯.消力池深的简化计算法[J].人民长江,2012,43(15):77-79,91.
[13]刘刚,滕凯.梯形断面均匀流水深的近似计算公式[J].水利与建筑工程学报,2012(1):41-44.
[14]滕凯,周辉.弧底梯形明渠正常水深的简化计算法[J].黑龙江八一农垦大学学报,2012,24(5):85-88.
[15]滕凯.标准门洞形过水断面临界水深的简化算法[J].华北水利水电学院学报,2012,33(5):1-3.
[16]张志昌.水力学[M].北京:中国水利水电出版社,2011.
[17]王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社,1999.
[18]阎凤文.测量数据处理方法[M].北京:原子能出版社,1988.

