基于RBF神经网络的年蒸发量预报

张德同，李韩笑

（1.吉林省水文水资源局白城分局，吉林白城137000；2.中水珠江规划勘测设计有限公司，广东广州510610）

1 引 言

蒸发量是影响流域水资源规划、优化调度与管理及水资源评价的重要水文要素，蒸发量预报对于及时了解旱情，指导农业合理灌溉，预防地下水位过低引起的地面次生盐碱化，具有重要意义[1]。

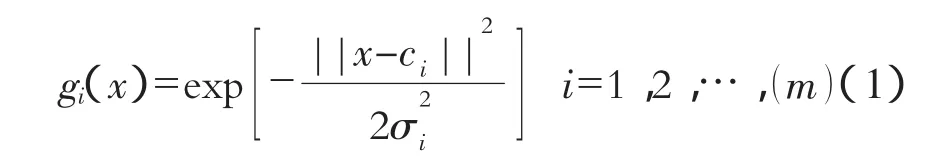
2 方法及原理

径向基神经网络(Radial Basis Function Neural Network)，简称RBF神经网络，是在20世纪80年代末由J.Moody和C.Darken提出的一种神经网络，在人脑中局部调整和相互覆盖接受域的生物学基础而建立的。因此，RBF网络是一种典型的局部逼近网络，RBF网络具有无局部极小点的特性，且有唯一最佳逼近的优点，但在网络构造及训练算法的设计与优化上面还需要进一步研究[2]。

RBF网络是3层的前向网络，第1层是输入层，由输入数据组成；第2层是隐含层，其中用径向基函数进行计算；第3层是输出层，从隐含层到输出层进行线性变换，目前已证明3层的RBF神经网络可以满足任意精确度逼近连续函数[5]。

RBF学习过程为2个阶段，第1阶段，实现从x→gi（x）的非线性映射，最常用的径向基函数是：

式中：x是n维输入向量；σi决定第i个基函数中心点的宽度；ci是第i个基函数的中心；m是隐含层的节点数，||x-ci||表示x和之间的距离。

第2阶段，输出层实现从gi（x）到y的线性映射，即：

式中：ωi为第i个隐层节点到输出神经元的连接权值；θ为第k个输出神经元的阈值。

3 模型应用

研究区位于干旱半干旱地区，属典型的温带大陆性气候，根据嫩江大赉站1970—2012年观测资料：年平均降水量为420 mm，年平均蒸发量1615 mm。研究区远离海洋，降水量少而集中，蒸发强烈。因此，蒸发量预报对于合理利用干旱区有限的水资源，提高水资源利用的社会效益、经济效益和生态效益具有重要意义。

该例中蒸发量属单因素序列，为了防止出现对学习过的数据拟合较好，而对未学习过的数据拟合不好的情况，采用滚动式学习和预测，因此经自相关分析，遵循AIC准则，在显著性95%水平下，确定自回归阶数为6，即每年的蒸发量与前6年的蒸发量密切相关。所以选取前6年的蒸发量作为输入，当年蒸发量作为输出。这样，将1970-2012年资料生成样本分37组，将前27组用于训练样本，后10组用于检验样本。

建立输入层为6个节点，输出层为1个节点的神经网络模型。调用MATLAB中的newrb（）函数编制计算程序，利用已调试好的程序对网络进行训练。运行程序，经27次训练误差达2.363×10-26，小于给定允许误差，网络收敛，此时训练宽度为2.5，隐含层神经元个数为27，训练次数为27次。

一个预报的好坏关键要看它对真实情况的逼近程度，因此在将模型用于预报前还要进行预报检验。采用未参加建模的2003-2012年蒸发量进行预测检验。并建立BP网络从检验结果对两者进行了进一步地分析比较，其预测结果见表1。

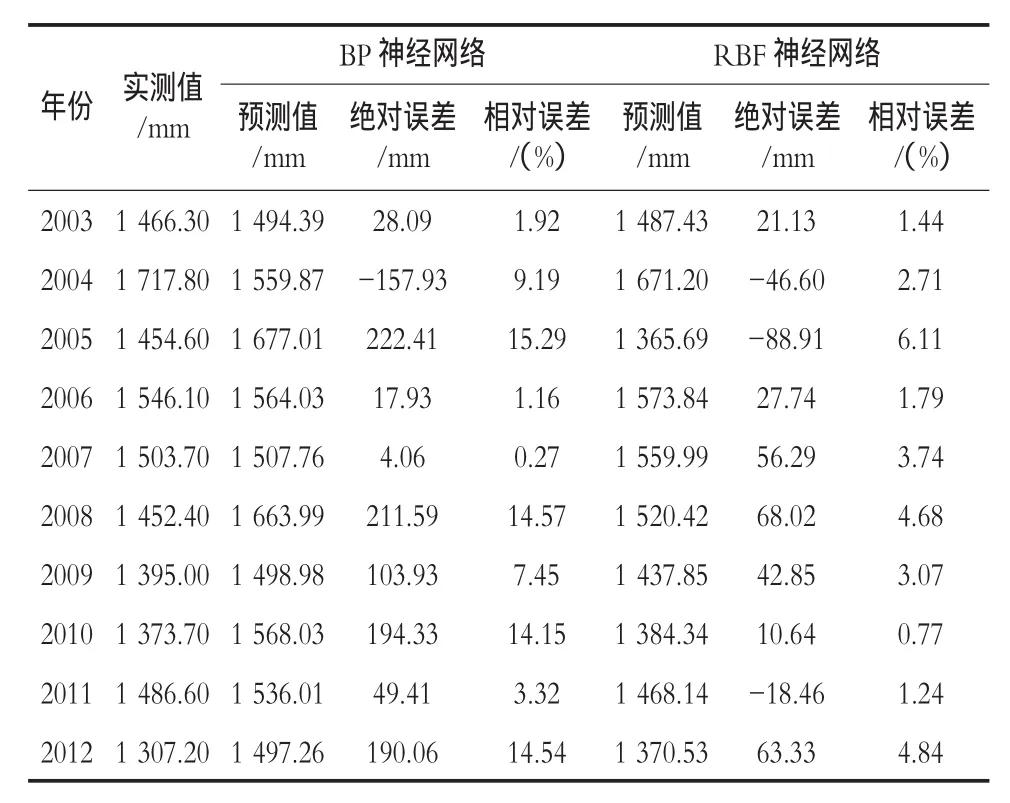
表1 RBFNN和BPANN模型精度检验统计表

从表1可看出，BP和RBF神经网络模型蒸发量预报效果均不错，其最大绝对误差分别为222.41 mm和68.02 mm，最小值分别为4.06 mm和0.77 mm，平均相对误差分别为8.19%和3.04%，虽然两种模型均可应用于该区蒸发量预测，但RBF神经网络模型预报精度略高于BP神经网络模型，可以更有效地对蒸发量进行预报。

图1 2014～2023年预报年蒸发量曲线

用经过精度检验的RBF神经网络模型，对嫩江大赉站2013—2022年的年蒸发量进行预报。年蒸发量的预报值和曲线见图1。从图中可以看出，该地区年蒸发量呈上升趋势，且上升幅度越来越大。年蒸发量是分析旱情的主要因素，旱灾不仅严重影响农业生产的稳定发展，还成为许多大中城市进一步发展的制约条件，因此，必须合理利用该区水资源，做好防旱抗旱措施，以确保工农业生产的发展及城市的安定。

4 结 论

1）径向基函数网络是典型的局部逼近网络，具有很强的非线性映射功能，能较好地反映蒸发量时间序列的内在变化规律，文中运用RBF神经网络对嫩江大赉站的年蒸发量进行了分析和预报。结果表明RBF神经网络能很好的预报年蒸发量。

2）BP和RBF神经网络预测蒸发量时，平均相对误差分别为8.19%和3.04%，可见，同BP网络比，RBF网络预测精度更高。另外，RBF神经网络稳定性更好，训练速度更快。RBF神经网络模型原理简单、使用方便，可以有效地弥补物理模型的不足，而且对于不同地区具有普适性，为蒸发量的预报提供了一种行之有效的方法。

［1］黄克明，张国忠.水文预报的神经网络模式分类预报方法［J］.武汉大学学报(工学版)，2003，36（1）：21-23.

［2］杨晓华，杨志峰，沈珍瑶.水环境非线性时序预测的高精度 RBF 网络模型［J］.水科学进展，2005，16（6）：789-791.

［3］黄国如，胡和平，田富强.用径向基函数神经网络模型预报感潮河段洪水位［J］.水科学进展，2003，14（2）：158-162.