考虑在途库存成本的班轮空箱调运优化
杨华龙,张欣迪,王瑞娟,张 燕
(大连海事大学 交通运输管理学院,辽宁 大连 116026)
0 引 言
班轮运输是集装箱航运基本形式,具有装卸效率高、减少货差及货损等优势。随着经济全球化和多式联运的飞速发展,班轮运输在国际海上贸易中的优势日益体现,但同时班轮公司的经营环境越发复杂,经营管理难度也随之加大,其中的一大难题便是空箱调运问题。每年全球集装箱空箱调运量占集装箱总运量的20%以上,空箱调运已成为班轮公司运营管理中最常见最棘手的老大难问题。如何合理地调运空箱已成为班轮公司降低运输成本、改善经营状况的关键因素。
自从W.W.White,等[1]首先利用运输规划理论开展空载运输工具优化调配的研究以来,内陆集装箱空箱调运优化的方法日趋完善;T.G.Crainic,等[2]建立了内陆空箱运输系统的确定型模型和随机型模型;K.Homberg,等[3]运用网络流方法对铁路空箱调运进行研究;汪传旭,等[4]研究了单箱种集装箱陆上调运模型,通过Storm软件求解对空箱需求和供给的随机性进行确定化处理。在海运班轮空箱调运的研究方面,W.S.Shen,等[5]以是否租箱或还箱为决策变量建立了网络优化模型,并基于该模型为班轮公司建立了解决空箱调运问题的决策支持系统;丁敏,等[6]采用了启发式算法研究了海上空箱调运;周红梅,等[7]结合运输规划理论和航运经济学理论,借鉴铁路空车调度优化模型的研究,建立集装箱空箱调运优化模型;施欣,等[8]利用Petri网理论和Games软件包对海运集装箱空箱调运进行动态模拟仿真。
上述空箱调运问题的研究,大都忽略了空箱在运输途中产生的在途库存持有成本,从而低估了因空箱调运而产生的总成本。宋若辰,等[9]以空箱在途库存成本最小为优化目标,构建空箱在途库存成本优化模型,但该研究尚未对包括空箱运输、租赁和在途库存在内的空箱调运总成本进行优化控制。此外,现有文献主要探讨的是班轮一个航班的空箱调运优化问题,对班轮运营一个决策期内多个航班的空箱调运优化问题尚缺乏全面系统的研究。为此,笔者结合近洋班轮运输多港挂靠循环航线实际,在考虑空箱在途库存成本的条件下,以空箱调运总成本最小为目标,研究决策期内滚动多航班的空箱调运优化问题。
1 问题描述
在集装箱班轮运输中,承运人将集装箱重箱从始发港运抵目的港交给收货人,收货人卸完货物后,便将集装箱空箱交还给承运人。由于普遍存在的货流不平衡现象,所以,集装箱在完成货物运输给客户带来方便的同时便会成为空箱,空箱的再利用则要求没有任何效益的空箱调运。在运输途中的空箱对班轮公司而言属于自有资产在途库存的范畴,此时集装箱船可看作一个“移动的仓库”,船上装载的空箱可看作存储在这个“仓库”里的货物。在途库存成本与资金的时间价值有关,它不像运输成本那样有实实在在的费用支出,它具有一定的“隐蔽性”,因此很容易被企业忽视[9]。在集装箱班轮运输领域,在途库存成本与库存持有成本类似,若在途库存占公司资产的比例过大时,就会降低公司的赢利性:一方面,公司需要支付由在途库存产生的相关现金成本,如保险、报废、损坏等,这会降低企业的净利润;另一方面,在途库存的增加会降低资产周转率,还有可能造成其它更好的投资机会丧失。
空箱在途库存成本包括以下几类:①资金成本,班轮公司在途库存空箱的持有占用了可以用于其他投资项目的资金,包括公司内部资金和从公司外部获得的资金,它属于在途库存投资的资金成本,是对于可能丧失的获利机会的反应,属于机会成本;②保险成本,保险成本是在途库存成本的重要组成部分之一,由于集装箱在运输、装卸和存储过程中可能会发生各种意外事故而造成损失,所以班轮公司都会给集装箱办理保险。空箱在途保险成本就是指班轮公司支出的保险费在空箱运输过程中的分摊;③管理成本,班轮公司为了更加有效地管理集装箱,对集装箱的使用动态作实时监控,往往投入大量的资金开发集装箱定位系统,此部分花费的成本在空箱在途运输过程中的分摊,构成了空箱在途管理。另外,班轮公司经常在港口雇佣当地代理进行空箱的进出口操作业务,支付给代理的费用在空箱在途运输过程中的分摊也属于管理成本。再有,其他的零散费用如空箱修理保养费、设备交接费、铅封制作费等的分摊也是空箱在途管理成本的组成部分。
在近洋海运贸易中,班轮公司根据实际情况大都选取多港挂靠循环航线,由于内贸箱通常不允许走国际航线,所以在一条近洋班轮航线上存在着某些港口间没有重箱和空箱运输,比如在由分属两个不同的国家或地区港口组成的多港挂靠航线上,同端港口间不允许有重箱和空箱运输,且航线的方向和班轮挂靠的港口顺序固定。因此,笔者考虑在途库存成本的近洋多港挂靠班轮航线空箱调运优化问题可以描述为:班轮公司在运用重箱舱位预售等方法获得一个决策期内每个航班每个港口的空箱需求和供给量的条件下,通过优化近洋多港挂靠航线上各港的空箱调运和租赁,在保证各港决策期内某一个航班经过重箱进出口和空箱调运以及做出空箱租赁决策后的空箱保有量满足下一航班的重箱出口需求的前提下,使得包含空箱在途库存成本、调运成本、租箱成本在内的空箱调运总成本最小。
结合近洋多港挂靠航线的集装箱班轮运输实际,笔者做以下基本假定:①在一个决策期内每个航班每个港口的重箱运输量为已知;②班期(发船间隔期)固定,且船舶能按时到港和离港;③只考虑20英尺箱;④率先满足重箱运输,若船舶有多余舱位再进行空箱运输;⑤首先考虑港口间的空箱调运,若仍无法满足需求,再从缺箱港当地租箱公司租箱;⑥若需要租箱,班轮公司与租箱公司签订的是短期租赁合同,租期从该航班开始起至本决策期结束,并且不考虑租赁箱在运输过程中产生的成本,只考虑租金;⑦每期的调运只为满足最近的一个需要空箱调运的航班,不考虑给未来预留空箱以备后用;⑧港口的堆场容量和码头前沿的堆存能力能完全满足需要;⑨决策期内航线上各港口间的贸易不平衡会形成航线一端为空箱需求港集合,另一端为空箱供给港集合,且同端港口间没有重箱和空箱运输。
2 模型建立
为了便于问题的建模与求解,引入以下参数和变量:
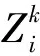
在班轮运输中,为了保持班期稳定,班轮公司通常将船舶的一个航次周期设定为班期的整数倍(亦即航线配船的数量)。这样,航班和派船之间便有如下关系:若求余函数mod(k,P)=p≠0,则第k航班由第p艘船舶执航(k=1,2,…,K;p=1,2,…,P-1);若mod(k,P)=0,则第k航班由第P艘船舶执航。
船舶到港卸下的重箱需要经过拆箱、货主提货等过程才成为空箱,所以在下一航班时才可利用;并且,因为要保证准班和高效,从他港调运来的空箱也只能在下一航班才可利用。结合班轮航运实际可知,第k航班在各空箱供给港调运至各空箱需求港的空箱必须满足下一航班(由航次周期和班期的关系可知此时的航班编号应为k+P+1)这些需求港的空箱需求,同时,决策期开始前各个需求港的初始空箱保有量必须满足前P+1个航班的装箱需求,因为在此期间从其它港口调运过来的空箱和被卸空的重箱还不能被利用。因此,在一个含有K个航班的决策期内,班轮公司若能获取各个航班的重箱运输需求,则为本决策期第1至第K-P-1航班制定空箱调运方案,为第K-P至第K航班制定租箱方案。当第K-P-1航班的空箱调运结束后,决策期相应地向后滚动,下一决策期便从第K-P航班开始至第2K-P-1航班结束,此时,下一决策期内需为第K-P至第2(K-P-1)个航班制定空箱调运方案,为第K+1至第2K-P-1航班制定租箱方案,以此类推。

(1)
港口j在第1航班卸空的重箱还不可利用,故可以调出的空箱为:
(2)
在第k航班(k≥2),港口j可以调出的空箱为:
(3)

由此,可以建立以下多航班空箱调运整体优化模型,目标函数是使空箱在途库存成本、调运成本和租箱成本三者之和最小。
目标函数:
约束条件:
s.t.
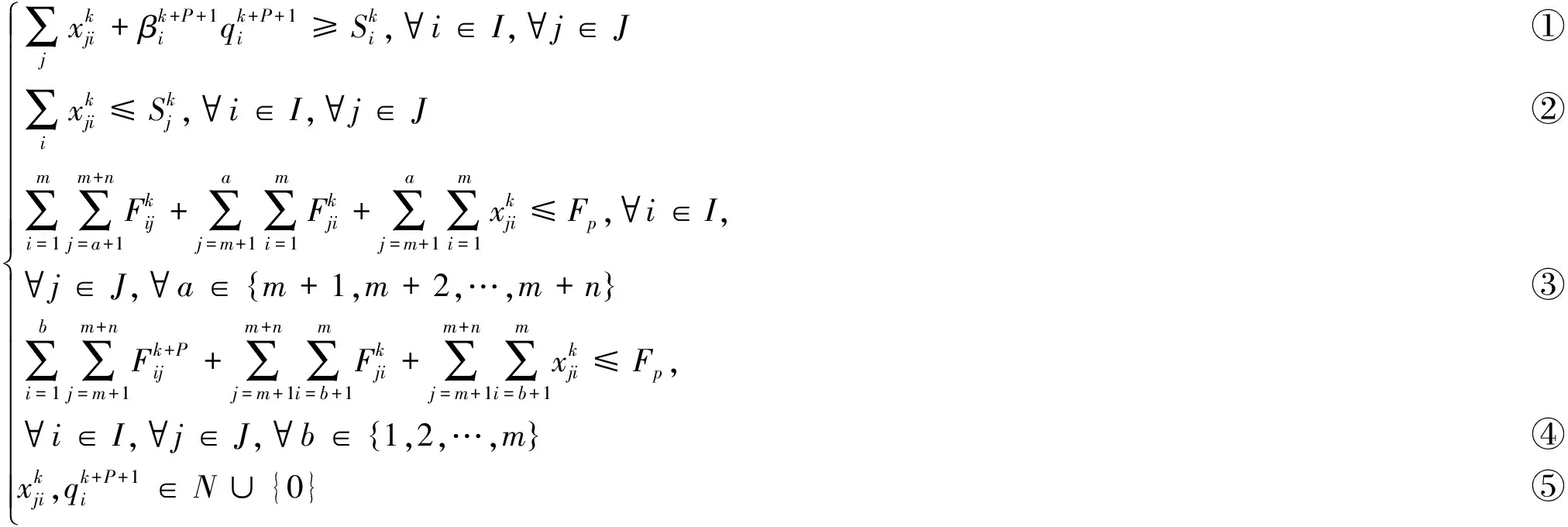

上述模型为整数规划模型,利用lindo软件包便可以求解。
3 算例分析
某班轮公司经营着一条有5个挂靠港口的近洋班轮航线(其中I端有2个港口,J端有3个港口),
班轮运输航线结构如图1。
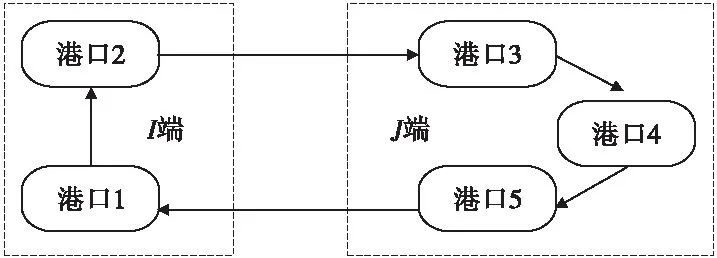
图1 班轮运输航线结构Fig.1 Shipping route of liner
公司在该航线上投入了2艘3 600 TEU的集装箱船舶进行运营,班期为每周1班,每个航次为14 d。船舶挂靠港顺序情况如图2。
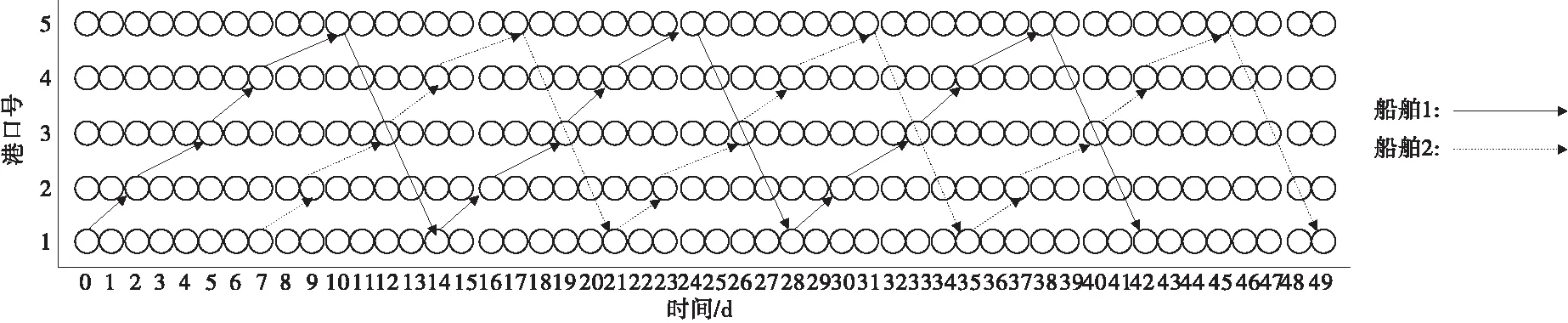
图2 船舶挂靠港顺序Fig.2 Sequence of vessel calling ports
假定空箱在途库存资金成本为1.1 USD/d,保险成本为0.6 USD/d,管理成本为0.5 USD/d。已知空箱运输成本及包括6个航班的决策期内各航段的重箱运输需求量如表1。

表1 各航段重箱运输量及运输成本Table 1 Full containers’volume and transportation costs ineach leg /TEU
各港口的初始空箱保有量、空箱装卸作业成本和租箱成本数据如表2。

表2 各港口基本数据Table 2 Base data of each port
由上述航次周期、班期之间的关系、空箱调运的实际情况以及制定调运方案的航班数与租箱方案的航班数关系可知:在本算例含6个航班决策期中,可以为第1~第3航班制定空箱调运方案,为第4~第6航班制定租箱方案。而下一决策期便从第4航班开始,至第9航班结束,并依此滚动下去。
根据港口初始空箱保有量以及重箱进出口箱量,若仅以满足每个航班每个港口空箱需求为前提,逐个航班制定空箱调运方案,可以得到调运方案如表3,在租箱方案方面,仅为第5航班在港口2租128箱。此时,总成本为764 258美元。

表3 一个可行的空箱调运方案Table 3 A feasible scheme of empty containers allocation /TEU
按照笔者构建的考虑在途库存成本的多航班空箱调运模型,利用Lingo11.0对进行求解,则可以求得前3个航班的空箱调运方案如表4,在租箱方案方面,仅有第5航班在港2需租用128箱,其余都没有租箱。此时,总成本为762 888美元。

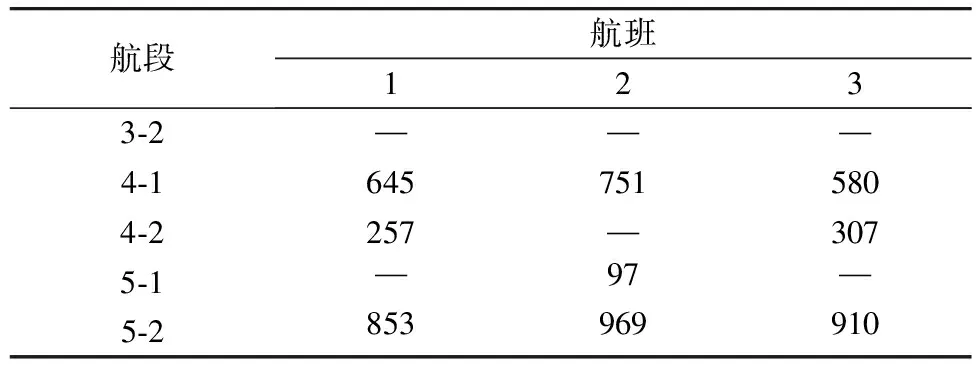
表4 优化后的空箱调运方案Table 4 Optimized scheme of empty containers allocation /TEU
(续表4)
航段航班1233⁃2———4⁃16457515804⁃2257—3075⁃1—97—5⁃2853969910
对上述两种调运方案进行比较,可以发现考虑空箱在途库存成本的整体优化模型得出的方案可节省成本1 370美元。随着航班数的滚动增加,班轮公司的效益会更加明显。
4 结 语
笔者针对近洋班轮运输多港挂靠循环航线,在考虑空箱在途库存成本的条件下,基于成本控制的思想,通过分析空箱在途库存成本和空箱调运成本的构成,在满足客户重箱和空箱需求的前提下,综合考虑空箱在途库存、运输、租赁等成本因素,建立了近洋多港挂靠航线下的滚动多航班空箱调运优化模型,通过优化航线上各港的空箱调运和租赁,使得包含空箱在途库存成本、调运成本、租箱成本在内的空箱调运总成本最小,从而可以滚动地给出班轮公司在一个决策期内的最佳空箱调运及租箱方案。
笔者研究了班轮公司在一个决策期内空箱供需已知情形下的空箱调运决策问题。今后应进一步探讨在空箱供需不确定情形下的空箱调运优化问题。
[1] White W W,Bomberawlt A M.A network algorithm for empty freight car allocation[J].IBM System Journal,1969,15(2):147-169.
[2] Crainic T G,Gendreau M,Dejax P.Dynamic and stochastic models for the allocation of empty containers[J].Operations Research,1993,41(1):102-126.
[3] Kai Homberg,Joborn M,Lundgren T.Improved empty freight car distribution[J].Transportation Science,1998,31(2):163-173.
[4] 汪传旭,刘大镕,贺斌.随机条件下空箱调配模型研究 [J].交通运输工程学报,2001,1(3):119-122.
Wang Chuanxu,Liu Darong,He Bin.Stochastic model for the allocation of empty container[J].Journal of Traffic and Transportation Engineering,2001,1(3):119-122.
[5] Shen W S,Khoong C M.A DSS for empty container distribution planning[J].Decision Support Systems,1995(15):75-82.
[6] 丁敏,孙文一,顾伟红.集装箱空箱调运的启发式算法优化研究[J].中国航海,2008,3(1):75-78.
Ding Min,Sun Wenyi,Gu Weihong.Research on the optimization of empty containers allocation based on heuristic algorithm[J].Navigation of China,2008,3(1):75-78.
[7] 周红梅,方芳.航运集装箱空箱调运优化模型的研究[J].武汉理工大学学报,2000,27(3):384-387.
Zhou Hongmei,Fang Fang.Research on the optimization model of empty container distribution[J].Journal of Wuhan University of Technology,2000,27(3):384-387.
[8] 施欣,刘桓江.基于Petri网的集装箱空箱调运仿真分析[J].交通运输工程学报,2002,2(3):97-102.
Shi Xin,Liu Huanjiang.Simulation of collection and allocation of empty containers based on Petri net[J].Journal of Traffic and Transportation Engineering,2002,2(3):97-102.
[9] 宋若辰,赵一飞.班轮公司集装箱空箱在途库存控制研究[J].重庆交通大学学报:自然科学版,2012,31(4):890-894.
Song Ruochen,Zhao Yifei.Study on liner operators’ controlling of empty containers’ in-transit inventory[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(4):890-894.

