灰色系统模型在大坝变形预测中的应用
鄢永辉
(安徽省宁国市水务局,安徽宁国,242300)
灰色系统模型在大坝变形预测中的应用
鄢永辉
(安徽省宁国市水务局,安徽宁国,242300)
为解决大坝安全监测中变形预测的问题,以某大坝坝顶监测数据为例,介绍了灰色GM模型预测的基本方法,采用MATLAB程序建立了GM(1,1)和GM(2,1)模型,分别对某大坝坝顶视准线部分监测点的变形量进行了预测。将预测值与实测值进行对比分析可知:采用GM(1,1)和GM(2,1)模型得到的预测结果均能很好地拟合实测值,预测精度高,利用该模型在实际工程中加以应用是可行的。
灰色系统模型;大坝变形;GM模型
0 引言
水库大坝在保障和促进国民经济发展中发挥着巨大的作用,对其进行安全监测并定期根据观测资料进行分析研究以评定大坝安全运行状况具有重要意义。
现有的大坝监测资料分析方法如多元回归分析方法、神经网络方法等都建立在大样本数据基础上,对短期或有残缺的资料无能为力,而且由于种种原因,我国相当部分大坝存在观测数据残缺或由于处在施工、蓄水初期而缺乏长期观测资料的问题。此外,由于大坝变形受诸多因素的影响,这些因素往往具有随机性和难以解析的非线性,应用各种模型都存在着模拟困难、计算复杂、工作量大等不足及问题[1,2],对大坝变形做出准确可靠的预测显得十分困难。
灰色系统理论是一种研究“部分信息已知,部分信息未知”的“小样本”、“贫信息”、不确定性问题的方法[3]。根据灰色系统理论可以建立相应的灰色预测模型。已有学者针对灰色模型的预测精度和预测合理性问题进行了探讨[4]。如果将影响大坝变形的各种因素看成一个系统,则该系统的内部信息和特征既有已知的也有未知的,故可把该复杂系统看成是一个受噪声干扰的具有物理原型的灰色系统,适用灰色系统理论,近年来已有人将该理论用于大坝变形预测,取得了一些成效[5]。以往在大坝变形预测中采用的灰色系统模型多为GM(1,1)模型。以某水库大坝的坝体变形监测数据为例,采用MATLAB程序建立了GM(1,1)和GM(2,1)模型,分别对该大坝坝顶视准线部分监测点的变形量进行预测,并对两种预测模型的生成系数取值进行了分析。
1 工程背景
某水利枢纽处于控制黄河下游洪水、泥沙的关键位置,是治理黄河下游的控制性骨干工程。工程开发目标以防洪、防凌、减淤为主,并兼顾供水、灌溉和发电。水库正常死水位为230 m,最高水位达到275 m,总库容为126.5亿m3。电站装机容量1 800 MW。在建设期间除埋设了大量内部观测仪器外,还布设了8条视准线。监测点均为强制对中标墩,标墩下部设有水准标志[6]。
大坝坐标系采用施工坐标系,其纵轴与大坝轴线重合,因此沿坝轴线方向(即X坐标)变形量较小,主变形方向为垂直于坝轴线方向(即Y坐标),所以只对变形点的Y坐标进行变形分析。这里以坝顶视准线上的809、811、817三处监测点(每半月观测一次)为例进行分析。变形量成果见表1。
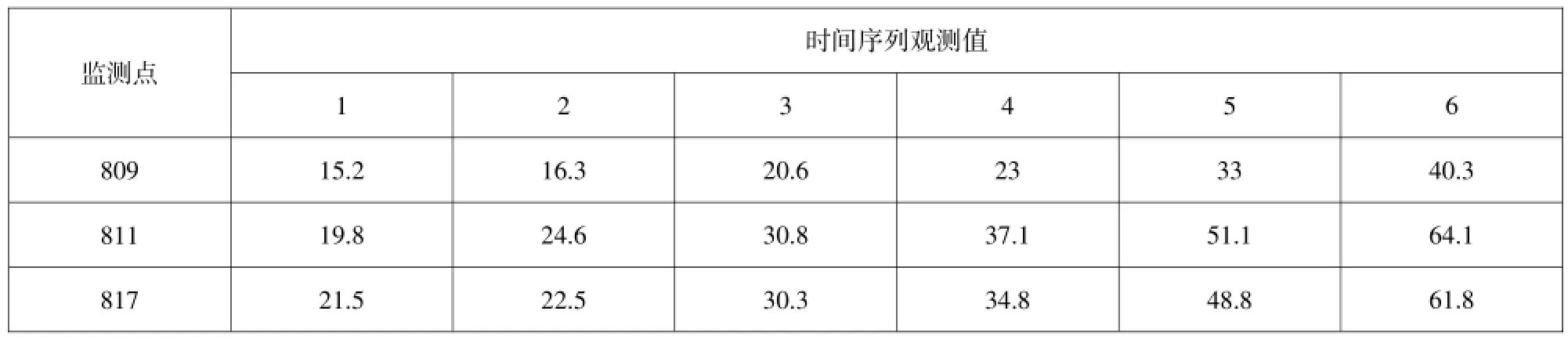
表1 坝顶视准线809、811、817三监测点变形量成果表Table 1 Measured deformation values by the collimating line on dam crest
2 GM模型预测在大坝变形预测中的应用
采用GM(1,1)模型预测的一般方法如下[7]:设原始数据列为:
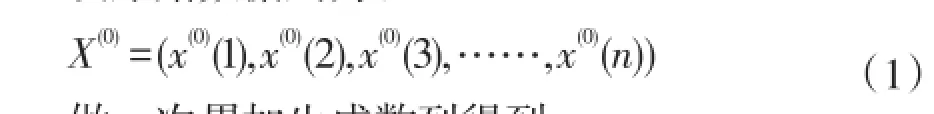
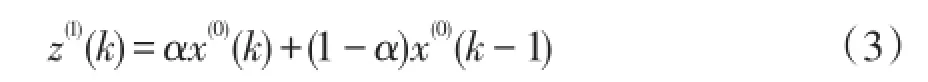
其中,生成系数α∈[0,1],一般取α=0.5则有均值生成数列:
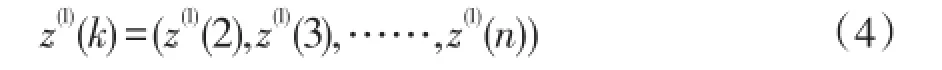
建立GM(1,1)模型方程:
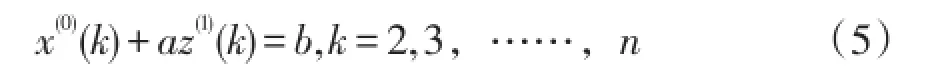
其白化微分方程为:

式中,a称为发展系数;b称为灰作用量。求解白化微分方程得:
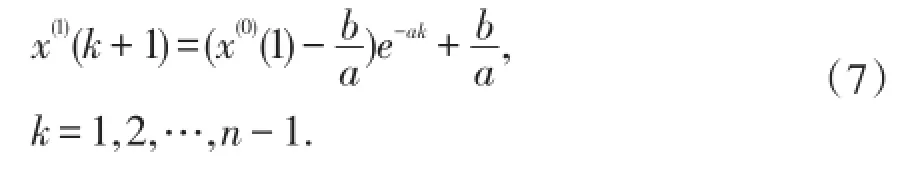
其中a、b的值由最小二乘法得到。则预测值为:
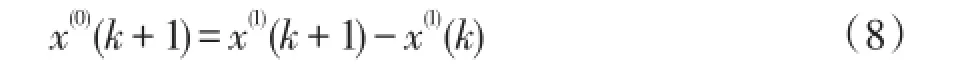
GM(2,1)模型是比GM(1,1)高阶的灰色预测模型,GM(2,1)模型与GM(1,1)模型建立方法类似,不同之处在于其模型方程为:
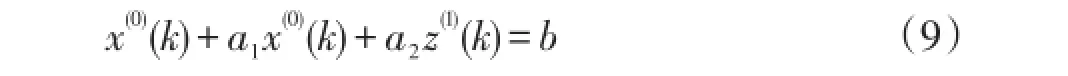
其白化微分方程为:

其中a1、a2、b的值由最小二乘法得到。
以表1中的原始数据列作为模型输入值,根据上述步骤编制MATLAB程序,运算得到GM(1,1)和GM(2,1)模型预测结果。各监测点观测值与预测值变形对比曲线见图1~3。
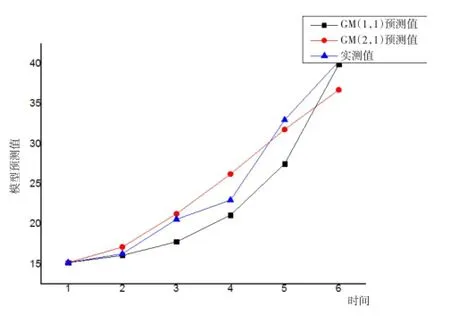
图1 809监测点变形预测值与实测值Fig.1 Predicted values and the measured values by the moni⁃toring point 809
令残差为ε,计算:

可知以上各预测值残差均不超过10%,采用GM(1,1)和GM(2,1)得到的预测结果均能较好地拟合实测值,预测精度高,利用GM模型对大坝变
形进行预测是可行的。
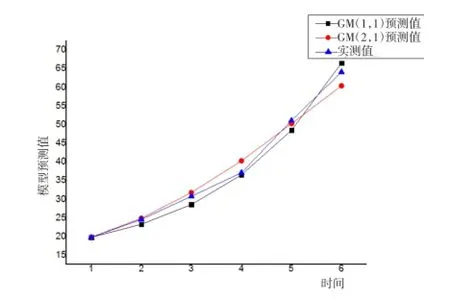
图2 811监测点变形预测值与实测值Fig.2 Predicted values and the measured values by the moni⁃toring point 811
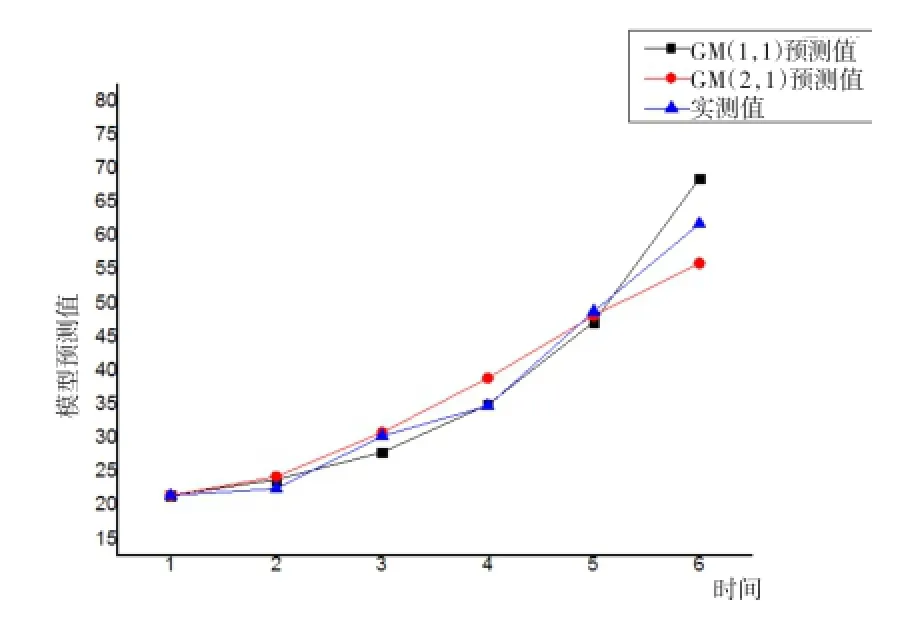
图3 817监测点变形预测值与实测值Fig.3 Predicted values and the measured values by the moni⁃toring point 817
3 生成系数对GM模型精度的影响
从GM模型建立的过程可以看出,生成系数α的取值对生成的均值数列乃至预测结果都存在影响,然而一般GM模型中对生成系数的合理取值并没有讨论。下面以809号监测点监测数据为研究对象,在[0,1]的范围内改变生成系数的取值,分析生成系数α的取值对GM(1,1)模型和GM(2,1)模型预测精度的影响。生成系数α依次取0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1时,GM(1,1)模型和GM(2,1)模型预测误差变化情况如图4所示。
由图4可以看出,当生成系数α在区间[0,1]的范围内变化时,GM(1,1)模型和GM(2,1)模型的预测误差均存在一个先减小后增大的过程,不同之处在于GM(2,1)模型的平均相对误差变化幅度不大,而GM(1,1)模型的平均相对误差存在一个幅度较大的变化过程。可知在使用GM模型对大坝变形进行预测时,存在一个最优生成系数α’,若生成系数取值不当,会导致相当大的误差。在实际工程中若采用GM模型,可首先进行试算。即选择一系列生成系数α对标高进行预测,将预测结果与已有的实测数据进行对比,选择预测结果与实测数据拟合最好的一个生成系数,用于后续滚动预测。
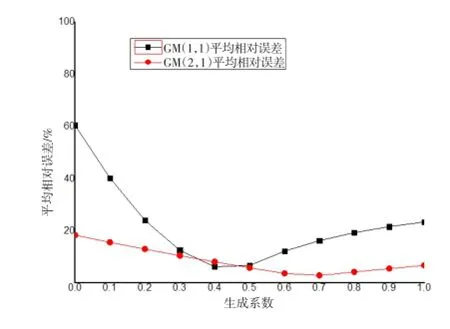
图4 不同生成系数下GM预测模型平均相对误差Fig.4 Average relation error of the GM model with different generating coefficients
4 结语
介绍了灰色GM模型预测的基本方法,并以某大坝坝顶监测数据为例,建立了灰色GM(1,1)和GM(2,1)预测模型分别对大坝进行预测,将预测值与实测值进行对比分析可知:采用GM(1,1)模型和GM(2,1)模型得到的预测结果均能很好地拟合实测值,预测精度高,利用GM(1,1)模型和GM(2,1)模型对大坝变形进行预测都是可行的。
对两种模型建立过程中的生成系数进行了分析,发现当生成系数α在区间[0,1]的范围内变化时,GM模型的预测误差存在一个先减小后增大的过程,且GM(1,1)模型误差变化幅度明显大于GM(2,1)模型。在实际工程中,若采用GM模型,建议首先利用前期已有的观测结果试算检验,确定合理生成系数取值,再用于后期变形的预测。 ■
[1]王新洲,范千,许承权,李昭.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报·信息科学版,2008,(5):469-471.
[2]张建新,蒋波.常规测量方法监测大坝变形的几个问题[J].大坝与安全,2012,(4):38-41.
[3]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:社会科学出版社,2004.
[4]谢乃明.灰色系统建模技术研究[D].南京:南京航空航天大学,2008.
[5]王勇,胡平,申莲,王汉中.GM(1,1)改进模型在大坝位移预测中的应用[J].云南水力发电,2011,27(2):28-30.
[6]胡光乾,蒋金虎,邱文华,等.小浪底水利枢纽大坝外部变形监测及资料分析[J].水力发电,2004,(9):49-51.
[7]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.
This paper introduces briefly the principle and the forecasting steps by use of GM model in which the prediction of practical monitoring data based on MATLAB is realized.The prediction results are well consistent with those by filed measurement,and the practical application value of this predic⁃tion method is proved.As well,the paper discusses the generating coefficients and some effective conclu⁃sions are drawn.
grey system model;dam deformation;GM model
TV698.1
B
1671-1092(2014)05-0032-03
2014-03-07
鄢永辉(1972-),女,安徽省宁国市人,工程师,从事水利设计与建设管理工作。
Title:Analysis and application of GM model in the prediction of dam deformation//by YAN Yong-hui// Bureau of Water Resources of Ningguo City,Anhui Province

