一种实现弹体感应磁场补偿的仿真方法研究

王丽黎，尹文超

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

在地磁匹配导航系统中，载体自身干扰磁场的分析与补偿是一个关键问题。根据飞行器上的磁干扰的类型可以建立磁干扰的数学模型，模型中含有一系列的系数，在飞行器上的仪器都固定的条件下，这些系数是固定的。测得需要的数据就可以推导出磁补偿系数，利用这些系数可以求出飞行器周围引起的干扰磁场大小，从而在地磁场未知的情况下得出真实的地磁场值。

目前国内在磁场补偿方面的研究主要集中在概略分析[1]和算法的研究[2-4]，而针对基于电磁场仿真模型和数值计算方面的研究却很少，少数单位仅仅研究了缩比模型周围的磁场分布[5],还没有基于真实模型的仿真补偿研究。针对目前在磁补偿方面还没有电磁仿真研究的情况，本文使用Ansoft Maxwell有限元软件，仿真出物体在不同磁导率的情况下以及不同磁力计放置位置时的测量总场值，依据这些测量值可以求出弹体外表面任意点及材料在任意磁导率下的补偿系数，并利用这些系数估计出背景地磁场。

1 导弹磁场补偿模型分析与软件建模

1.1 弹体磁场模型求解分析

根据飞行器磁干扰的Tolles-Lawson数学模型及表达式[6]作为分析模型，本模型以仿真感应磁场为主，暂不考虑恒定场和涡流场，建立弹体坐标系如图1所示。L轴与弹体纵轴平行，首部为正；T轴与L轴垂直，V轴与TOL平面正交，向下为正。α、β、γ分别为 He与3个坐标轴之间的夹角， 其方向余弦分别为 cosα、cosβ、cosγ。He为地磁场矢量，感应出来的干扰场投影到地磁场方向大小为 Hid，化简后为表达式(1)：

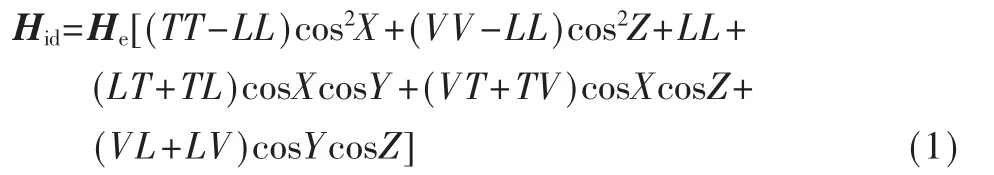
其中感应场有 6个补偿系数 (TT-LL、VV-LL、LL、LT+TL、VT+TV、VL+LV),磁力计测量总场 Hz减去地磁场 He可得干扰场Hid，再利用地磁场矢量与弹体坐标系3轴夹角和干扰场大小来求出补偿系数。

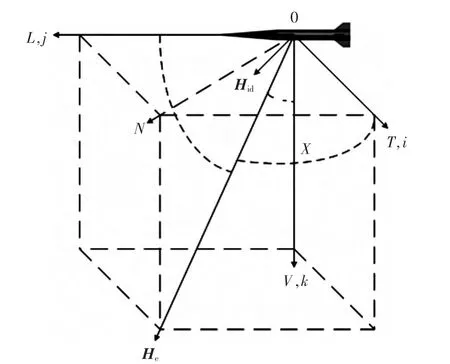
图1 弹体坐标系示意图

1.2 模型的建立

在Maxwell中建立Tolles-Lawson模型，弹体总长度为7 m，前半部分弹头为圆锥型总长度3 m，后半部分弹体包括尾翼总长度4 m，半径为30 cm，大小和形状接近真实模型，使用永磁体加上适当的矫顽力来形成一定方向的均匀磁场，如图2所示。弹体在均匀磁场会受到磁化并在周围产生感应磁场。由于软件所仿真出的磁场值结果输出都以Global坐标系为准，在软件仿真中通过改变地磁场对物体的作用方向来模拟弹体在空间内与地磁场形成任意角度，将软件输出值作为模拟磁力计的测量值。模型的材料及属性参数如表1所示。

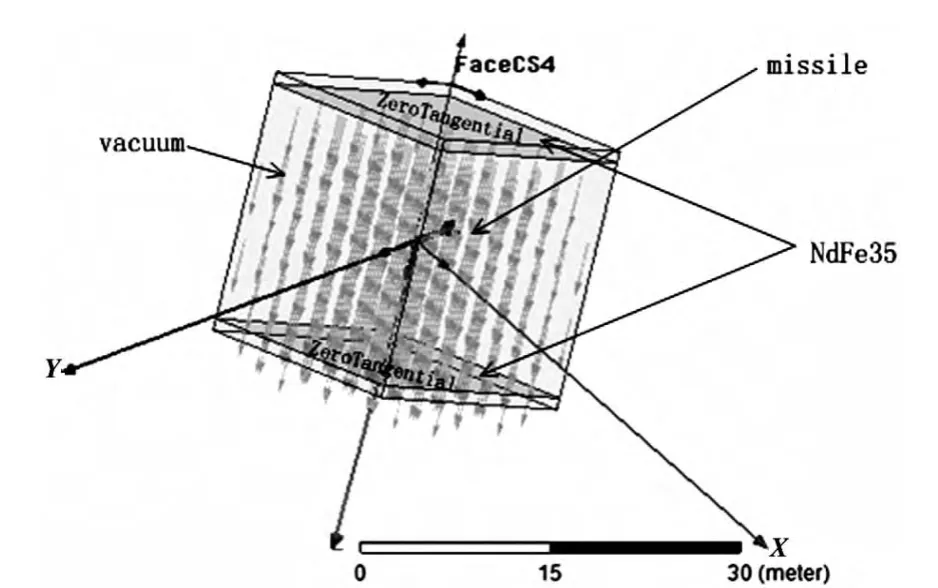
图2 仿真模型

表1 模型的材料属性

2 磁场补偿技术的仿真与计算

2.1 仿真原理和计算步骤

磁干扰表达式(1)中有6个未知补偿系数，求出方程的解最少需要6个方程，将式(1)写成矩阵形式(2),左列为弹体在地磁场n种姿态时的干扰场大小，右侧为对应的姿态矩阵和感应系数的乘积，这里使用最小二乘法求解。

仿真时令初始磁场方向垂直XOY面向下,再令磁场方向相对Y轴逆时针旋转形成参数为α的角度，之后相对Z轴逆时针旋转形成参数为β角度,如图3所示。

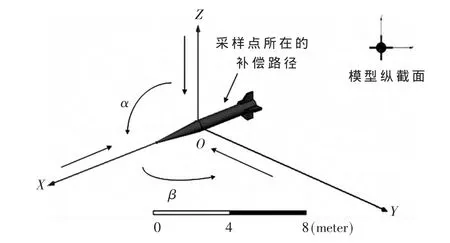
图3 模型的侧面和纵截面

本文研究磁力计安装在弹体表面的情况，通过软件来实现多点采样。这样可以找出磁力计安装在某个位置使得补偿效果达到最好，本例取距离弹体表面5 cm沿弹体纵轴线的一条路经作为磁力计放置一系列的测量位置，目的是要算出这条路径上所有采样点的补偿系数，最后再求出所有位置的补偿误差，确定补偿效果最佳的磁力计放置位置。

在软件求解前需要进行参数设置,如表2所示。

表2 求解参数设置

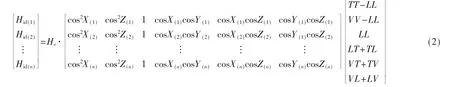
感应磁场是在静态的恒定磁场作用下产生的，因此选用静磁场求解器。零边界条件保证了外部没有磁场并且内部磁场方向单一且垂直于边界面。参数化α1和β1的目的是形成对物体不同作用方向的磁场，每个组合对应一个弹体在地磁场中的一个姿态，由于弹体模型分别关于XOY面和XOZ面对称并且地磁场反向作用时仅仅改变最后磁场值的符号，所以这里参数化0～90代表地磁场在一个象限内作用物体，通过maxwell的参数设置step可以包含任意磁场对弹体的作用方向，以此来模拟飞行器在空间中的姿态。参数化 α2和β2形成的磁场作为验证，利用前部分求出的系数和后部分求出的总场来估计地磁场大小，最后将估计出的磁场值与形成的背景地磁场相比较来评价补偿结果。将上述参数设置好后即可利用软件进行数值计算。

2.2 数据的后处理

导出测磁补偿路径上所有点在相对磁导率为1～5时弹体处于地磁场中所有姿态的地磁场三分量BXBYBZ和模值MagB，在这条路径上采样700个点作为磁探头的测量点，磁场大小为50 266 nt，同时计算出式(2)中的cosX、cosY、cosZ,表达式左边的干扰场大小等于该磁探头位置的测量值MagB减去地磁场大小得出。利用角度 α1、β1、step=10时参数化的结果求出所有位置的 6个补偿系数，再利用角度 α2、β2、step=36时参数化的结果求出所有位置的补偿系数来估计背景地磁场，并与真值He对比得出每个位置补偿后的剩余标准差，最后对补偿结果进行分析。

3 对仿真方法可靠性的验证

下面建立一个简单的静态磁偶极子模型对软件的计算精度进行验证和分析。之后,以一个简单实验来验证利用本文的补偿方法还原真实地磁场。

3.1 验证精度

Ansoft公司的Maxwell 3D是一个功能强大、结果精确、易于使用的三维电磁场有限元分析软件。

根据电磁场理论，磁偶极子模型[7]在侧向空间中形成的磁感应强度大小为式(3)，轴线方向形成的磁感应强度大小为式(4)：

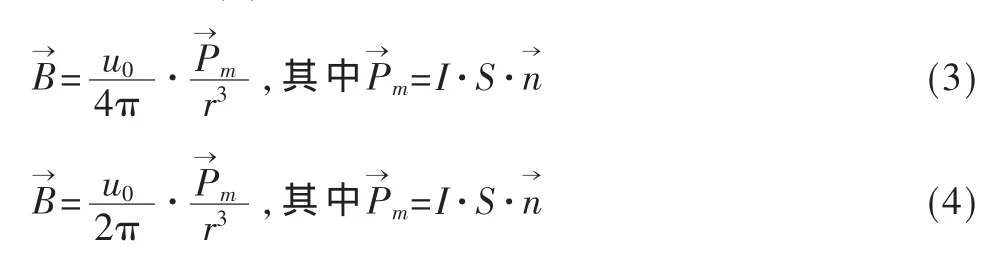
根据这一理论在磁场中建立磁偶极子模型，其磁场分布如图4所示。将仿真出来的有限元解与理论值比较，如表3所示。有限元解与理论值的误差百分比很低，说明数值计算精度较高，有限元解较接近实际理论值。

3.2 实验分析

实验在一个可以形成单一方向均匀磁场的磁屏蔽箱内进行。

实验时保证磁力计与物体相对位置不变，通过增加亥姆霍兹线圈的电流控制最终形成了51 807 nt的电磁场，磁场沿磁屏蔽箱的轴线方向，通过不断改变物体在磁场内的位置状态测得每个状态对应的磁场三分量和总场强度。这个实验在一个平面内进行一些角度的旋转，测量值、补偿值和真实值的结果如图5所示。

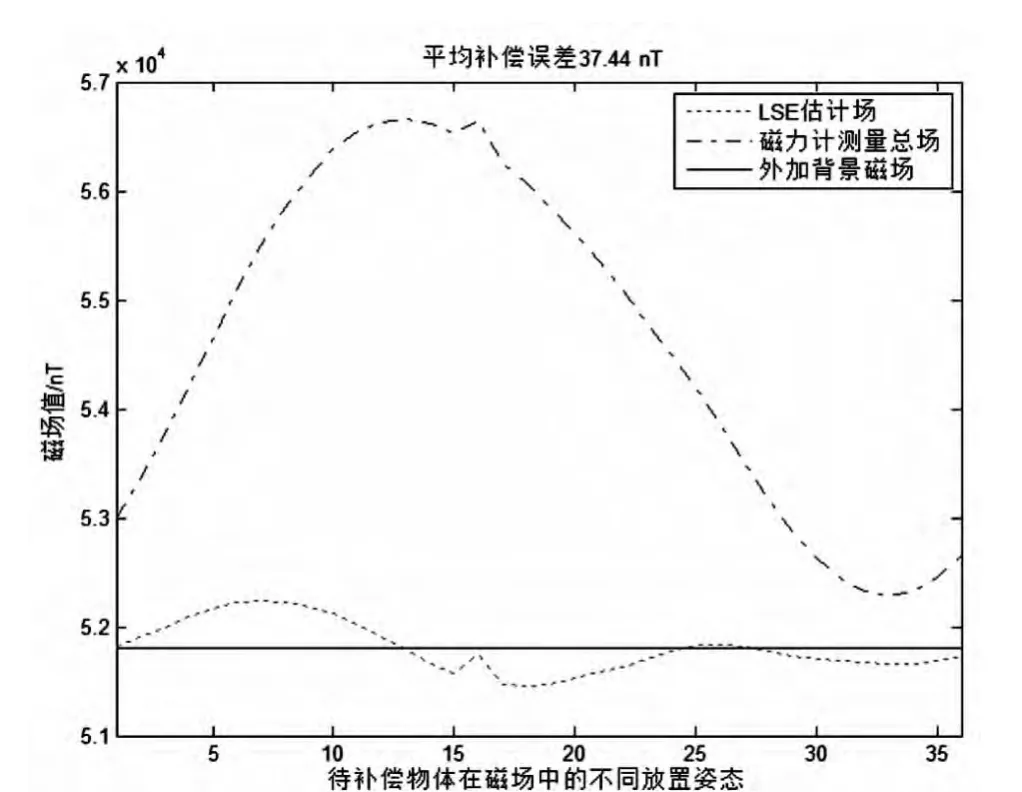
图5 测量和补偿结果

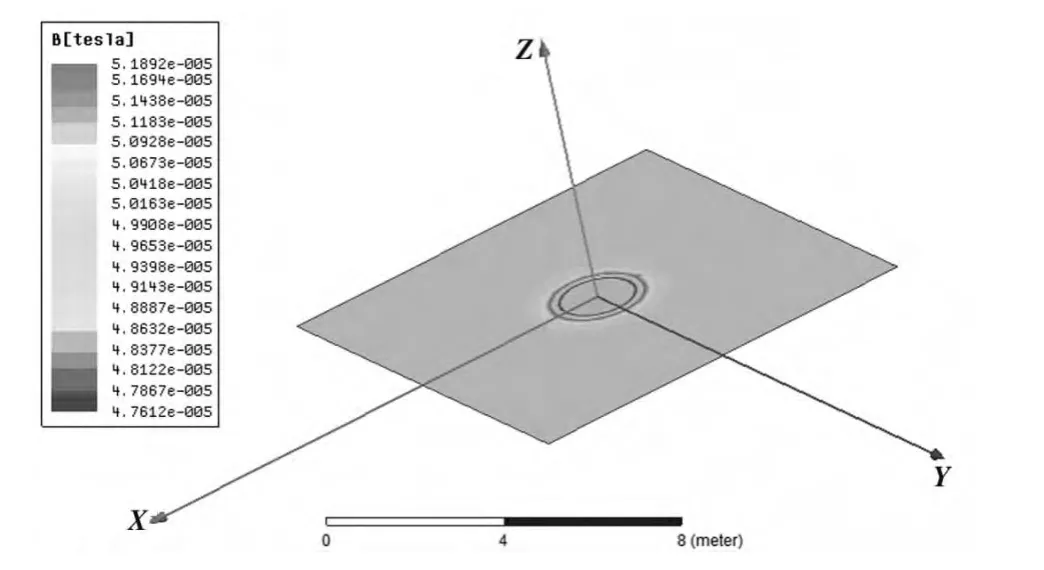
图4 磁偶极子模型在空间中产生的磁感应强度

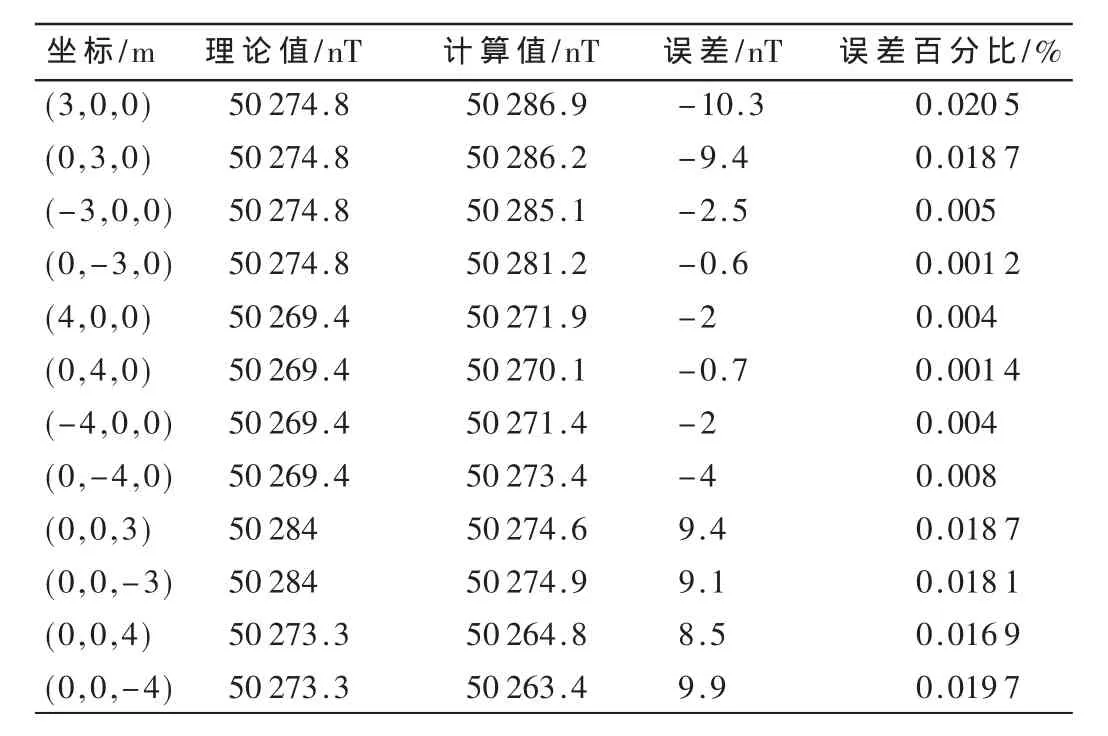
表3 有限元解与理论解比较

图5显示了物体在磁场中36个状态的补偿结果，平均误差比较小，直观地反映了本文的补偿方法是可行的。

该实验说明，通过不断改变被补偿物体在磁场中的不同状态并利用最小二乘法可以近似地估计外部地磁场的大小。

4 仿真结果及其分析

在Maxwell软件中仿真生成的背景地磁场He的大小为50 266 nt，在补偿路径上采样700个测量点作为测磁点，同时计算了物体在磁导率从2～5每个点的补偿结果，对结果的分析评价如图6所示，图表的纵坐标为对弹体表面点在参数化(α2和β2)姿态时的补偿剩余标差。

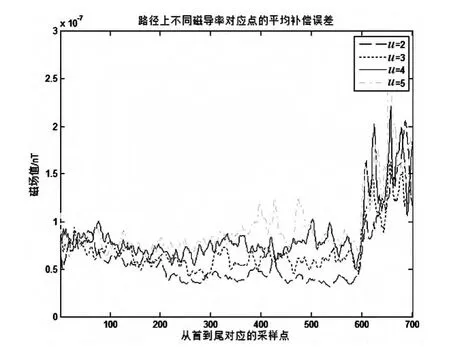
图6 某路径在同一地磁场作用下不同磁导率下的补偿结果

通过对仿真数据的处理，得出了沿着弹体表面某路径在同一地磁场作用下不同磁导率的补偿结果，同时得出了材料在相对磁导率在2～5时对多种飞行姿态补偿后的平均误差。其一，磁导率越大，补偿后的误差相对偏大，但并不是所有的补偿位置的补偿误差都随着磁导率的增大而增加；其二，基于本模型，弹体首部和弹体表面的补偿误差偏小，基本小于100 nT，而尾部的补偿误差较大。

本文通过电磁场仿真软件Ansoft maxwell仿真飞行载体空间中的感应磁场分布，并使用最小二乘法(LSE)进行参数估计，求出弹体表面空间某曲线上所有采样点的补偿系数并进行分析。本文提供了一种利用电磁场仿真软件建立Tolles-Lawson模型并补偿的方法，可以在不进行试验的情况下仿真研究感应磁场分布，实现了磁场补偿，并对多种姿态的补偿结果进行了综合评价。通过软件参数化设置，对仿真数据进行处理之后可以找到不同磁导率下模型的最佳补偿点。本仿真方法可以对任意形状模型在任意磁导率的情况下找出最佳补偿位置，以及磁力计在同一安装位置下找出补偿效果最好的材料相对磁导率，在工程中可为材料磁导率的选取和磁力计的安装位置提供依据。

[1]赵双求.UAV航磁系统及补偿研究[D].长沙：中南大学，2011.

[2]张坚,林春生,罗青,等.基于预测残差平方和的飞机干扰磁场模型求解[J].探测与控制学报，2010,32(5):74-78.

[3]庞学亮,林春生,张宁.飞机磁场模型系数的截断奇异值分解法估计[J].探测与控制学报,2009,31(5):48-51.

[4]伍东凌,陈正想,王秀.基于遗传算法的磁干扰补偿方法[J].探测与控制学报，2012,34(6):16-20.

[5]李永慧，张晓明，刘俊,等.某常规弹载体感应磁场分布的仿真技术研究[J].弹箭与制导学报，2012,32(4):181-184.

[6]LELIAK P.Identification and evaluation of magnetic field sources of magnetic airborne detector equipped aircraft[J].IRE Transactions on Airspace and Navigational Electronics，1961(8)：95-105.

[7]任来平,赵俊生,侯世喜.磁偶极子磁场空间分布模式[J].海洋测绘,2002,22(2):18-21.

[8]赵博，张洪亮.Ansoft 12在工程电磁场中的应用[M].北京：中国水利水电出版社，2010.