基于Kriging函数的KVPMCD在滚动轴承故障诊断中的应用

杨 宇 潘海洋 李 杰 程军圣

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

滚动轴承故障诊断实质上是一个模式识别的过程。而对于模式识别来说，其重点在于分类器的设计，分类器设计的好坏直接影响分类的结果。针对滚动轴承的故障诊断问题，已经有各种不同的分类器。

目前常用且已成熟的故障诊断分类器有神经网络和支持向量机等，但神经网络分类器具有一些缺陷，如网络训练速度慢、局部极小点和过学习，且非常依赖于经验和先验知识［1］；随后出现的支持向量机分类器虽然用途较广，但也存在一些难以解决的缺陷，如需要严格的核函数和参数调整［2］，而这些主观因素对分类结果有非常大的影响。尤为重要的是，这两种分类器都没有考虑所提取的特征值之间的内在变量关系。然而，在机械故障诊断中，特征值之间或多或少具有一定的内在关系，而且这种特征值之间的内在关系在不同的系统或类别（相同的系统在不同的工况下）间具有显著的不同。

基于特征值之间的这种内在关系，Raghuraj等［3］提出了一种新的模式识别方法——基于多变量预测模型的模式识别（variable predictive mode based class discriminate，VPMCD）方法，该方法的实质就是通过特征值之间的相互内在关系建立数学模型并完成分类。其中预测模型的建立是VPMCD分类器的核心部分，VPMCD模式识别方法采用4种回归模型建立预测模型，对于特征值较为规则的，其模型具有一定的实用性。但当特征值之间的关系较为复杂时，用这4种模型建立预测模型，会出现局部偏差，这样很难准确建立接近真实模型的近似模型，以至于所建立的VPMCD分类器分类精度达不到要求。

Kriging模型是一种估计方差最小的无偏估计模型［4－6］。Kriging模型由回归模型和相关模型组合而成，通过Kriging模型中的回归模型和相关模型随机组合，最终可以建立若干真实模型的近似模型，它们之间不同的组合建模将对结果产生很大影响［7］，从不同的组合模型中选出最理想的一个组合作为最佳预测模型，进而能充分反映特征值之间的关系，建立有效的分类器。

本文将Kriging模型引入机械故障诊断中，把Kriging模型应用于VPMCD中建立模型，从而建立基于Kriging模型的VPMCD分类器。即将Kriging模型应用于VPMCD方法中，得到基于Kriging的多变量预测模型（Kriging variable predictive mode based class discriminate，KVPMCD）模式识别方法。该方法首先采用Kriging模型中的回归模型和相关模型依次组合建立VPM数学模型，再以最小误差平方和最小为依据，建立KVPMCD的预测模型，从而建立KVPMCD分类器以用于分类识别。

1 KVPMCD模型

在机械故障诊断中，提取p个不同的特征值X＝ （X1，X2，…，Xp）来描述一个故障类别，由于特征值之间存在内在关系，因此，在不同的故障类别中，X1会受到其他特征值的影响而产生不同的变化，在此类问题中，特征值之间可能存在一对一的关系：X1＝f（X2）；或者一对多的关系：X1＝f（X2，X3，…）。为了识别系统的故障模式，需建立数学模型。VPMCD方法中，为特征值Xi定义的变量预测模型VPMi为一个线性或者非线性的回归模型，文献［3］中提出了4种数学模型。以p个特征值为例，对4种模型中任意一个模型采用特征值Xj（j≠i）对Xi进行预测，都可以得到

其中，特征值Xi称为被预测变量；Xj（j≠i）称为预测变量；e为预测误差；b0、bj、bjj和bjk为模型参数。式（1）称为特征值Xi的变量预测模型VPMi。

VPMCD的本质是利用特征值之间的内在关系，然后调用已存在的4种回归模型建立反映特征值之间真实关系的近似模型，但当特征值之间的关系比较复杂时，由于4种模型的条件限制，所建立的模型可能不能充分反映特征值之间的内在联系，因此，本文将Kriging模型应用于VPMCD中得到KVPMCD，Kriging模型中存在3种回归模型和6种相关模型，它们之间相互组合可以建立18种模型，其中的回归模型类似于VPMCD中的模型，构建了预测模型的主结构，6种相关模型则进行辅助，使得所建立的模型更加逼真，从而可以建立反映特征值之间复杂关系的KVPMCD模型，其KVPMCD模式识别方法步骤如下：

（1）对于g类分类问题，共收集n个训练样本，每一类样本数分别为n1，n2，…，ng。对所有训练样本提取特征量X＝ （X1，X2，…，Xp），每一类样本特征量的规模大小分别为n1×p，n2×p，…，ng×p。

（2）选择第k（k＝1，2，…，g）类训练样本的特征量Xj（i＝1，2，…，p）作为被预测变量，选择剩下的p－1个特征量Xj（j≠i）作为预测变量。

（3）令回归模型类型m＝1（Zero order polynomial、One order polynomial、Two order polynomial 3种模型分别用数值1、2、3标记），相关模型的类别r＝1（Exponential、Generalized exponential、Gaussian、Linear、Spherical、Cubic spline 6种模型分别用数值1、2、3、4、5、6标记），建立一个数学模型。

（4）先后分别令r←r＋1和m←m＋1，直至r＝R，m＝M结束。预测变量的组合方式共有M×R种可能，因此对于特征量Xi可建立nk＝M×R个数学方程。

（5）对于每一个特征量Xi建立的nk个方程，然后把第k类训练样本的特征量进行回代，利用Kriging模型得到特征量Xi的预测值Xipred。

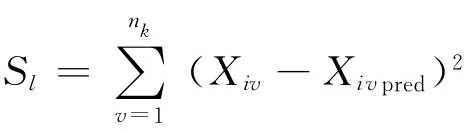
（7）令k←k＋1，循环步骤（3）～ （7）直至k＝g结束。至此，在回归模型类型为m和相关模型类型为r的情况下，g个类别的所有特征量都分别建立了变量预测模型VPM（k）i，其中k＝1，2，…，g表示不同类别，i＝1，2，…，p表示不同特征量。这些变量预测模型构成一个大小为g×p的VPM矩阵。

（8）将所有训练样本作为测试样本分别对每一个VPM矩阵进行回代分类测试，选择分类正确率最高的VPM矩阵所对应的回归模型类型和相关模型类型作为最佳变量预测模型的类型。至此，各种类别下的所有特征量的最佳变量预测模型的类型、预测变量都得以确定。

（9）选择测试样本，并提取其特征值X＝（X1，X2，…，Xp）。对于测试样本的所有特征值Xi（i＝1，2，…，p），分别采用变量预测模型对其进行预测，得到预测值。

2 基于KVPMCD的滚动轴承故障诊断方法

对于滚动轴承的故障诊断，特征提取是其中的关键环节，只有选择合适的特征才能准确区分滚动轴承的工作状态和故障类型。用来描述系统非线性特性的参数较多，复杂度相对较为简单；峭度和模糊熵也常用来处理非线性问题；最大李雅普诺夫指数可用来分析信号的复杂程度。因此，本文采用组合的方法，即提取信号的复杂度、峭度、模糊熵［8］和最大李雅普诺夫指数。它们之间可相互补充、相互印证，更有利于识别故障信号，增强可靠性。但这些指标对噪声较为敏感，为了降低噪声的影响，本文结合局部特征尺度分解（local characteristic scale decomposition，LCD）［9］方法，采用LCD降噪来获取降噪后的重构信号。

本文采用对原信号进行LCD分解后重构获得降噪后的信号，首先采用LCD得到N个内禀尺度分量（intrinsic scale component，ISC）信号。对每一个ISC求其与原信号的互相关性，得到相关系数值。由于白噪声信号与任何信号都不相关，原信号中包含的噪声信号毕竟很少，而且噪声信号在分解过程中进行了强迫对称分解，已不再是白噪声，所以它与原信号的互相关值接近于零。本文根据经验设定两个阈值，单分量ISC信号与原信号相关系数值大于阈值的区间，则被判定为有用分量，予以保留下来；相关系数值在阈值区间之内的被判定为伪分量，进一步判定；相关系数值小于阈值区间的被判定为噪声分量，直接剔除。然后进一步对伪分量进行自相关分析，如果自相关系数只在零点处取得较大值，其余皆很小，则可判定为噪声分量，否则判定为有用分量。最后把判定为有用分量的进行重构，以实现降噪。此方法为简单的降噪方法，目的就是得到含有噪声较少的信号，使得对提取的特征影响较小。

基于KVPMCD的滚动轴承故障诊断方法步骤如下：

（1）在一定转速下以采样率fs对滚动轴承正常、内圈故障、外圈故障和滚动体故障4种状态进行采样，每种状态采集N组样本。

（2）利用LCD降噪方法对原始振动信号进行分解降噪，得到降低噪声的重构信号。对重构信号分别提取复杂度、峭度、模糊熵、最大李亚谱诺夫指数作为特征值，组成特征值向量，每种状态下得到N×i阶的特征值矩阵。

（3）每种状态取M个样本作为训练样本，通过KVPMCD训练，建立预测模型

（4）剩下的作为测试样本，用训练好的数学预测模型对测试样本进行分类，根据KVPMCD分类器的输出结果来确定滚动轴承的工作状态和故障类型。

3 应用

3.1 UCI标准数据应用

UCI标准数据［10］是公认的验证数据，因此，为了验证KVPMCD方法的适用性，本文采用UCI标准数据进行测试，选取UCI标准数据中liver数据和pima数据两类进行试验。其中，liver数据包含6个特征值，两种状态；pima数据包含8个特征值，两种状态。首先分别任意选取liver数据和pima数据中的60组作为训练样本，任意选取40组作为测试样本。然后使用支持向量机、RBF神经网络、VPMCD和KVPMCD对训练样本进行训练。经过优化选择，所取RBF神经网络训练误差的平方和都为0.01；liver数据和pima数据的支持向量机折衷系数取1，核函数都采用RBF核函数；对于KVPMCD的相关模型参数theta，此处采用对训练样本进行交叉验证，通过比较识别率，选取theta＝0.15。最后通过4种分类器对测试样本进行分类，其分类结果如图1所示。

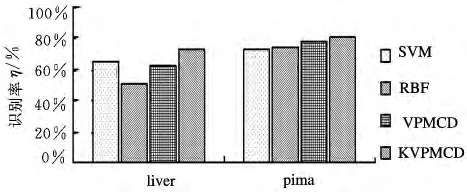
图1 两类UCI标准数据样本在4种分类器下的识别率

从图1中可知，尽管4种类分类器对liver数据和pima数据的分类识别率不是特别高，但KVPMCD还是显示其优越性，尤其是对liver数据，相对于其他3种分类器，识别率有较大的提高。

3.2 实例应用

为了验证KVPMCD在机械故障诊断中的应用，本文采用美国凯斯西储大学电气工程实验室的滚动轴承数据［11］，滚动轴承选用型号为6205－2RS型的深沟球轴承，转速为1772r/min，采样频率为48 000Hz，故障直径是0.018mm，故障深度是0.028mm，电机负载为0.746kW。机械设备运行时，其部件滚动轴承有可能会出现内圈故障、外圈故障或滚动体故障。因此，选取轴承正常、内圈故障、外圈故障和滚动体故障4类状态下的振动信号各100组数据。随机抽取其中的50组数据为训练样本，其余50组数据为测试样本。内圈故障下的滚动轴承振动信号如图2所示。

图2 内圈故障状态下滚动轴承振动信号时域波形

首先对信号进行LCD降噪处理，得到重构信号，然后提取重构信号的复杂度、峭度、模糊熵和最大李雅普诺夫指数作为特征值，对于复杂度和峭度，则直接提取特征值，模糊熵需要设置参数，如相似容限r、指数函数边界梯度n和维数m，经过优化选择［8］，取r＝0.2，n＝2，m＝2，最大李雅普诺夫指数选用wolf法［12］。提取特征值后，再进行模式识别。把训练样本分别通过VPMCD和KVPMCD训练，得到预测模型。对于KVPMCD的建模需要设置相关模型参数theta，本文采用训练样本交叉验证的方法得到相关模型参数theta，把训练样本分为5组，然后进行交叉验证，其验证结果如图3所示。

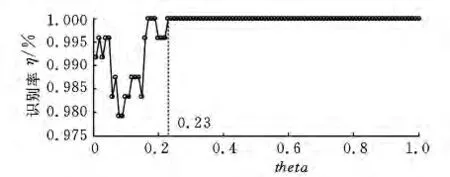
图3 各相关参数在交叉检验法下得到的识别率

通过图3可知，当theta的取值大于0.23时，其交叉验证识别率保持为100%，因此本文取theta＝0.23。为了比较VPMCD方法和KVPMCD方法在各种检验法下的识别精度，本文分别采用 Re－substitution（简称 RS）检验法、K－fold cross－validation（简称 K－CV）检验法和Jack－knife（简称JK）检验法进行验证，其中Re－substitution检验法能验证算法的自相容性，K－CV交叉检验法常用来测试算法的准确性，Jack－knife（简称JK）检验法是较为客观和严格的交叉检验法，是目前公认最好的交叉检验方法，能反映算法的推广能力。采用3种检验法分别对VPMCD和KVPMCD的性能进行检验，其中采用RS检验法检验所有数据的自相容性；K－CV交叉检验法用来检验测试样本的识别率；JK交叉检验法用来检验训练样本的识别率。另外引入的Kappa系数是一种计算分类精度的方法，其值越大，则表示分类效果越好。检验结果如表1所示。

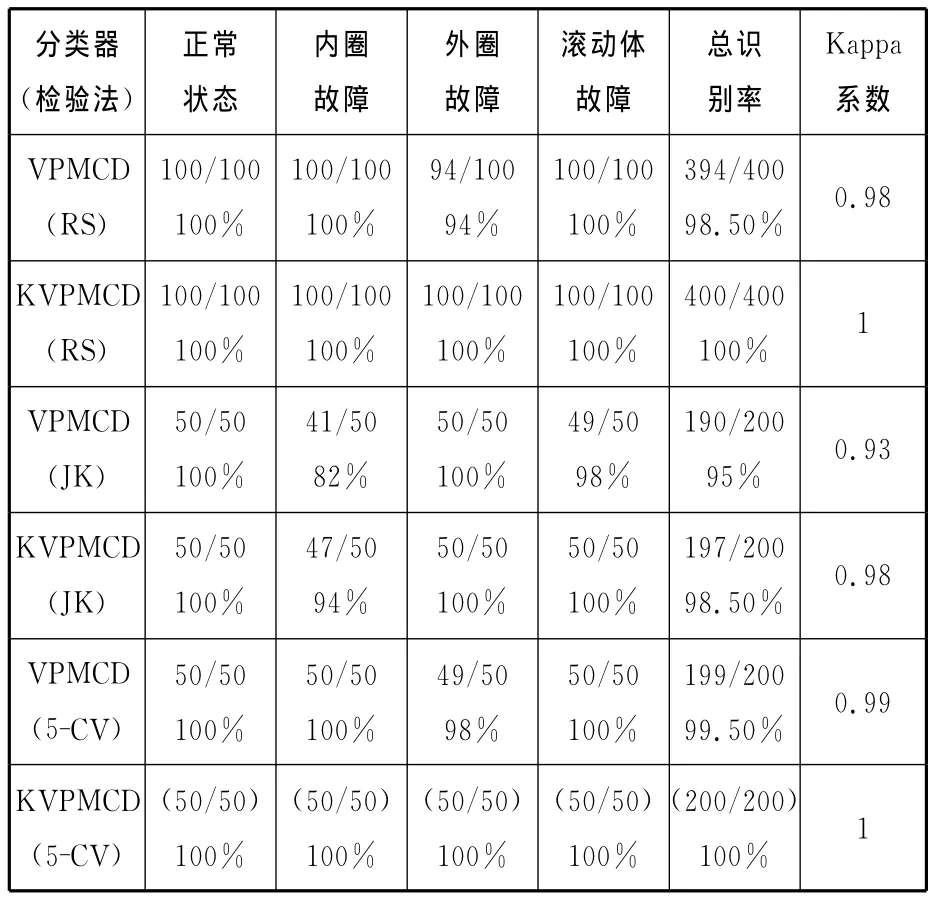
表1 3种检验法下的VPMCD和KVPMCD分类性能对比

表1显示了2种分类方法在3种检验法下的识别率和Kappa系数。通过测试，KVPMCD具有更高的自相容性和分类准确性，因此，在两类检验法下，KVPMCD无论是总识别率还是Kappa系数，均优于VPMCD方法。

另外，从识别精度方面来说明KVPMCD更加优越，参数不变，每种状态取50个样本训练，50个样本测试。首先通过训练样本建立4种状态的预测模型；然后把测试样本代入所建立的预测模型，求出每个样本特征值在各个预测模型下的估计值；接着求出每个样本在4种预测模型下的预测误差平方和，由于不同预测模型下得到的最小误差平方和数量级相差过大，因此，对得到的误差平方和求对数，如图4和图5所示，显示了部分样本在4种预测模型下的预测误差平方和对数值；最后比较每个样本在4种预测模型下得到的预测误差平方和，以最小预测误差平方和为依据进行分类。

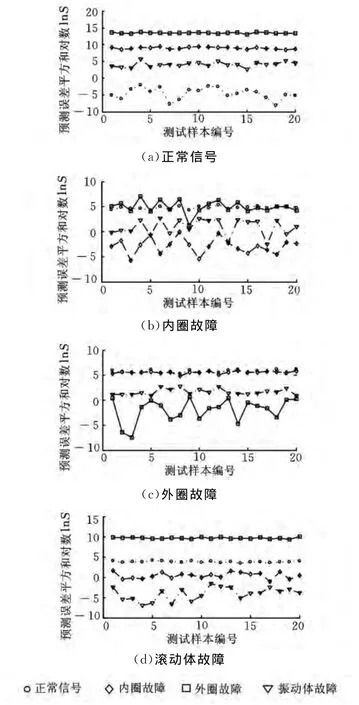
图4 VPMCD在滚动轴承各种状态下的识别精度

由图4可知，测试信号为正常信号时，在正常信号预测模型下得到的预测误差平方和与另外3种预测模型下得到的预测误差平方和相差较大，易判别；测试信号为内圈故障时，在内圈故障预测模型下得到的预测误差平方和与在滚动体故障预测模型下得到的预测误差平方和相差很小，几度出现交叉，致使出现错误分类；测试样本为外圈故障或者滚动体故障时，其效果也不是很好，因此，VPMCD虽然整体识别率较好，但识别精度并不是很好，容易出现错分。图5是KVPMCD的识别精度图，整体看，4种状态的预测误差平方和区分特别明显，没有出现错分现象。因此，从两个图中可以得出，KVPMCD比VPMCD有更高的识别精度。

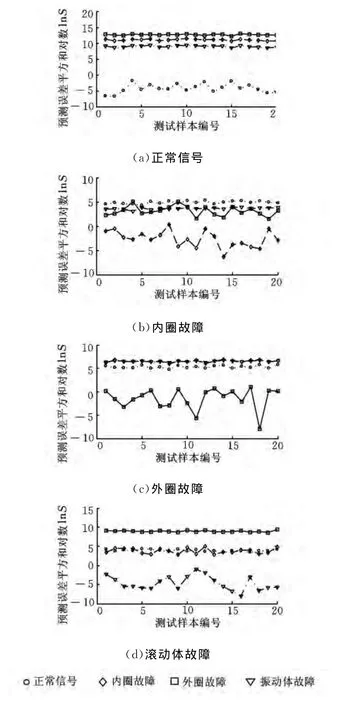
图5 KVPMCD在滚动轴承各种状态下的识别精度

综上所述，通过对VPMCD和KVPMCD分类器的检验，无论用UCI标准数据还是滚动轴承数据，以及无论用何种检验法识别率还是识别精度，都证明了KVPMCD方法能建立更加接近真实模型的近似模型，从而可以更加准确对样本的进行分类。

4 结论

（1）对所提取的特征值进行组合，即提取信号的复杂度、峭度、模糊熵和Lyapunov指数，它们各有不足，因此通过组合，使得它们相互补充，相互印证，更有利于诊断。

（2）VPMCD的预测模型建立，不受主观因素的影响，而在神经网络分类器和支持向量机分类器中。它们的结构、类型、参数及核函数选择往往都非常依赖于经验或先验知识。同理，KVPMCD类似于VPMCD，只需要设置“相关模型”中的相关函数参数，其设置较为广泛，不需要太依赖先验知识，因此，KVPMCD模式识别方法受主观因素的影响较少，所得分类结果较为客观。

（3）把Kriging模型应用于VPMCD中得到KVPMCD，VPMCD中4种回归模型对于特征值之间的内在关系较为复杂时，很难准确建立预测模型，KVPMCD中采用以回归模型为主题，相关模型辅助，从而建立更加真实地预测模型。

（4）对UCI标准数据中的两类数据若干状态和滚动轴承4种状态的信号的分析结果表明，Kriging模型和VPMCD相结合的KVPMCD可以有效的应用于模式识别，也证实其适用性，在对滚动轴承的试验中，该方法可以准确、有效地对滚动轴承的工作状态和故障类型进行分类，从而为滚动轴承的故障诊断提供了一种新的方法。

［1］ Wang Huaqing，Chen Peng.Intelligent Diagnosis Method for Rolling Element Bearing Faults Using Possibility Theory and Neural Network［J］.Computer ＆Industrial Engineering，2011，60（4）：511－518.

［2］ Fei Shengwei，Zhang Xiaobin.Fault Diagnosis of Power Transformer Based on Support Vector Machine with Genetic Algorithm［J］.Expert Systems with Applications，2009，36（8）：11352－11357.

［3］ Raghuraj R，Lakshminarayanan S.Variable Predictive Models－a New Multivariate Classification Approach for Pattern Recognition Applications［J］.Pattern Recognition，2009，42（1）：7－16.

［4］ Cressie N.The Origins of Kriging［J］.Mathematical Geology，1990，22（3）：239－252.

［5］ Gou Peng，Liu Wei，Cui Weicheng.A Comparison of Approximation Methods for Multidisciplinary Design Optimization of Ship Structures［J］.Journal of Ship Mechanics，2007，11（6）：913－923.

［6］ 张仁铎.空间变异理论及应用［M］.北京：地质出版社，2005.

［7］ Rana M，Andreas P.An Empirical Comparison of Kriging Methods for Nonlinear Spatial Point Prediction［J］.Mathematical Geology，2002，34（4）：365－386.

［8］ Chen Weiting，Wang Zhizhong，Xie Hongbo，et al.Characterization of Surface EMG Signal Based on Fuzzy Entropy［J］.IEEE Transaction on Neural Systems and Rehabilitation Engineering，2007，15（2）：267－272.

［9］ 程军圣，郑近德，杨宇.一种新的非平稳信号分析方法——局部特征尺度分解［J］.振动工程学报，2012，25（2）：215－220.Cheng Junsheng，Zheng Jinde，Yang Yu.A Nonstationary Signal Analysis Approach－the Local Characteristic－scale Decomposition Method［J］.Journal of Vibration Engineering，2012，25（2）：215－22.

［10］ Frank A，Asuncion A.UCI Machine Learning Repository［EB/OL］.（2010－05－03）.http：//archive.ics.uci.edu/ml.

［11］ Case Western Reserve University Bearing Data Center.Bearing Data Center Fault Test Data［EB/OL］.（2009－10－01）.http：//www.eecs.case.edu/laboratory/bearing.

［12］ Wolf A，Swift J，Swinney H，et al.Detemining lyapunov Exponents from a Time Series［J］.Physica D：Nonlinear Phenomena，1985，16（3）：285－317.