鱼雷航行终了漂浮姿态分析及工程计算方法

曾小凡, 蔡卫军, 徐新栋, 王改娣, 边 翔



鱼雷航行终了漂浮姿态分析及工程计算方法

曾小凡1, 蔡卫军1, 徐新栋1, 王改娣1, 边 翔2

(1. 中国船舶重工集团公司 第 705 研究所, 陕西 西安, 710075; 2. 山西平阳重工机械有限责任公司, 山西 侯马, 043002)

鱼雷实航试验中的安全回收与其航行终了的漂浮姿态密切相关, 直接关系到试验的成败。分析了影响鱼雷航行终了漂浮过程和漂浮姿态的主要因素, 给出了一种直观、简洁、实用的漂浮姿态工程计算方法, 并通过了试验验证。验证结果表明, 该方法正确、结果可信, 能够方便有效地应用在鱼雷工程设计和实航试验中, 并可为鱼雷总体结构布局、衡重参数匹配、试验回收方案设计等提供参考。该方法可推广应用于其他水下航行体的漂浮姿态计算。

鱼雷; 实航试验; 漂浮姿态; 工程计算方法

0 引言

一般情况下, 鱼雷实航试验使用的雷型配置有标准操雷和正浮力操雷2种, 无论哪种操雷(以下均称鱼雷), 鱼雷航行终了的安全回收一直是试验人员要解决和关注的重点问题, 如果回收延迟或无法回收, 就可能造成鱼雷丢失, 严重影响整个试验的顺利进行, 其损失不可估量。影响鱼雷安全回收的因素有很多, 对于采用捆绑式雷位指示装置的鱼雷, 航行终了的漂浮姿态直接关系到信号弹能否正常发射, 是影响鱼雷回收的主要因素之一[1]。

目前, 限于对鱼雷复杂外形进行非线性体积分的难度, 还难以用纯数学理论的方法对鱼雷的漂浮姿态进行计算。但是, 随着科学技术的进步和计算机技术的快速发展, 各种建模工具和计算软件在鱼雷工程设计上的应用越来越广泛, 其中, 利用UG工具凭借其直观、快捷、简单、方便等特点[2], 不但能够真实准确地描述鱼雷的3D实体模型, 而且可对鱼雷进行外形布局分析、质量特性分析和结构特性分析, 这为鱼雷漂浮姿态分析和计算提供了有力帮助。

本文针对与鱼雷安全回收密切相关的航行终了漂浮姿态问题进行分析, 借助UG工具, 给出一种鱼雷航行终了漂浮姿态的工程计算方法, 并通过实例进行了验证。

1 鱼雷航行终了漂浮过程及影响因素分析

通常, 鱼雷航行终了指动力系统停车, 且控制系统断电, 此时鱼雷处于无动力无控状态并开始进行自由漂浮运动。假设鱼雷航行终了的初始姿态呈水平状态, 其受力情况如图1所示。

图1 鱼雷航行终了初始姿态

图中:为重力;为浮力;X为重浮心间距。

对于图1 (a)重心在后的鱼雷, 在重力矩作用下, 雷头朝上开始上浮; 对于图1 (b)重心在前的鱼雷, 在重力矩作用下, 雷尾朝上开始上浮。一般情况下, 鱼雷航行终了时, 重心在浮心之后, 所以下面主要针对图1(a)的情况进行分析。

当图1 (a)中鱼雷头朝上上浮到浸没水中部分的排水量等于自身质量时停止上浮。为了便于分析, 假设鱼雷垂直上浮, 则上浮后的状态见图2。图中2为新的浮心。

从图2看出, 上浮后鱼雷浮心已经改变, 可能在重心之前, 也可能在重心之后, 这取决于正浮力大小和初始重浮心位置。

对于图2 (a)具有较小正浮力的情况, 浮心仍然在重心之前, 鱼雷处于相对稳定状态, 如果重心没有下移或侧移, 则鱼雷不再进行姿态调整, 并基本呈90°直立状态; 如果有重心下移或侧移, 则会倾斜一定角度, 角度大小与新的重浮心间距及下移量或侧移量有关。

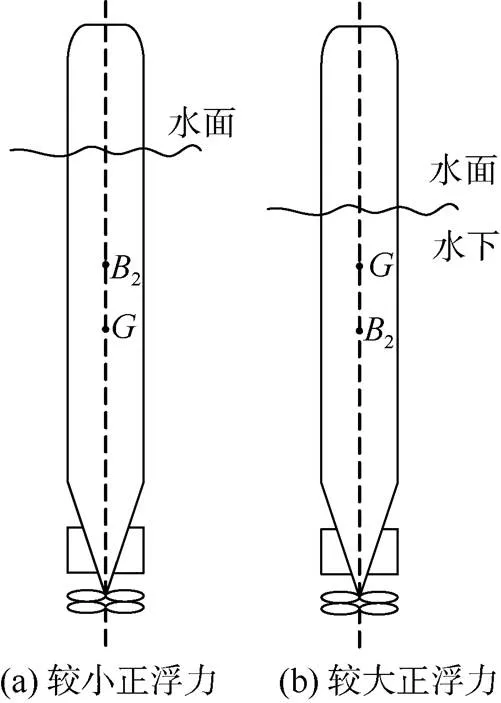
图2 鱼雷垂直上浮后状态

对于图2 (b)具有较大正浮力的情况, 浮心已移到重心之后, 属于一种动不稳定状态, 若存在重心下移量、侧移量或小扰动, 都将导致鱼雷倾斜, 并开始姿态调整, 以寻求新的平衡位置, 其姿态调整过程见图3。

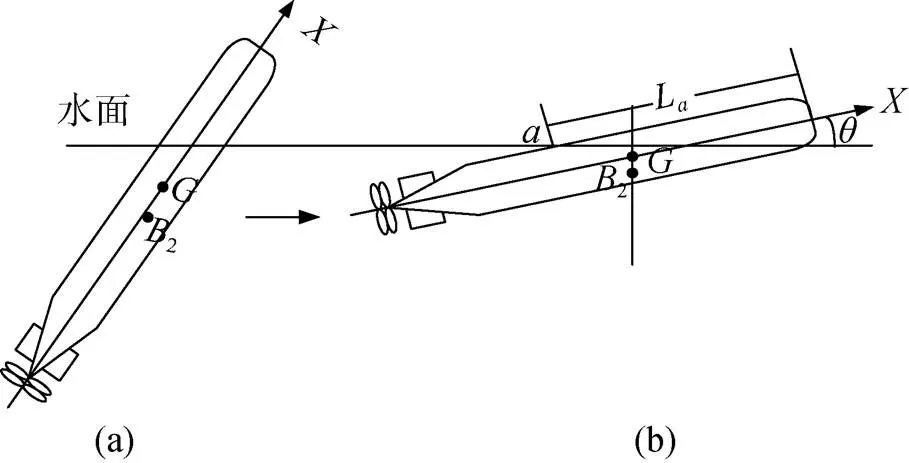
图3 新浮心在后的鱼雷姿态调整过程

根据上述分析可以看出, 影响鱼雷最终漂浮姿态的因素主要有鱼雷航行终了的质量、排水量、重心位置和浮心位置等。下面将主要对图3中描述的鱼雷航行终了漂浮姿态给出工程计算方法。

2 鱼雷漂浮姿态的工程计算方法

图3中, 鱼雷露出水面部分的体积与头部线型有关, 由于描述鱼雷头部线型曲线的复杂性, 对头部露出部分体积进行理论计算, 工作量很大, 在工程上难以快速实现, 不易推广应用。所以, 本文基于对鱼雷实物特性的了解和对航行终了漂浮过程的理论分析, 采用UG工具, 在创建了鱼雷实物3D模型基础上, 从工程应用的角度, 找出了一种计算鱼雷漂浮姿态的方法。

已知鱼雷航行终了的衡重参数如直径、长度、质量、排水量(全浮力)、浮心位置距前端面距离L、重心位置距前端面距离L、重心下移量y和水密度, 则其漂浮姿态计算步骤如下。

1) 计算正浮力

(1)

2) 计算露出水面部分体积

1=/(2)

3) 计算垂直状态时露出水面部分长度L1。 利用UG工具, 在操雷3D模型上, 从雷顶端面开始截取与体积1相等的部分, 该部分的长度即为鱼雷垂直浮起时露出水面部分的长度L1。

4) 计算水下部分浮心位置L2。截取水面部分1后, 剩下的水下部分排水量与重力相等, 所以, 水下部分的体积应为

2=/(3)

利用UG工具, 可得出水下部分的形心位置L2。

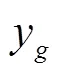
此时, 雷体纵轴与水平面夹角为

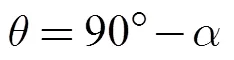
若L2>L, 则浮心在重心之后, 需按下面第6)步进行姿态调整计算。

6) 姿态调整计算过程。利用UG工具, 将鱼雷放置于水平状态, 采用截面法逐次对雷体截取与体积1相等的部分, 如图4所示。图中:为截取角;为截取高度。

实际操作中, 为了减小截取次数, 第一次从雷顶端面正下方某点开始斜向上截取体积为1的雷体, 然后计算出剩余雷体(水下部分)浮心位置L2。若L2>L, 则截取点向上移动, 继续沿截取方向截取体积等于1的雷体; 若L2<L, 则截取点向下移动, 继续截取体积等于1的雷体。

图4 鱼雷截面示意图

理论上,L2=L时停止截取, 但考虑到雷体重心下移或侧移, 所得到的浮心L2一般应在L左右偏差很小的位置上, 此时, 所对应的截取角就是鱼雷最终漂浮状态下纵轴与水平面的夹角, 截面与雷体的交线即为水线, 水线与雷体表面交点距雷顶端面的距离即为截取长度L。

3 计算方法验证结果

为了验证本文计算方法的正确性, 在此针对某型鱼雷的实航试验产品状态, 按照第3节计算步骤, 对鱼雷航行终了的漂浮姿态进行计算。

已知鱼雷航行终了重心位置L=1470mm, 浮心位置L=1385mm, 显然, 重心在浮心之后, 则鱼雷头朝上方开始上浮, 其稳定漂浮后的姿态计算过程和结果如下。

1) 正浮力=16 kg。

2) 露出水面部分体积1= 0.0158 m3。

3) 垂直状态下露出水面部分长度L1= 218 mm。

4) 水下部分浮心位置L2=1483 mm。

5) 由于L2>L, 需要按第3节中的第6)步逐次计算鱼雷漂浮姿态, 计算结果见表1。

表1 计算结果

从表1可以看出, 当截取点在雷顶端面中心(截取高度为0), 截面与中心线夹角为9.54°时, 剩余部分浮心为1469 mm, 与重心1470 mm基本重合, 此时, 可认为鱼雷稳定漂浮时纵轴与水面的夹角为9.54°左右, 头部的浸水线基本位于雷头的中心, 雷体表面露出水面的长度约964mm, 满足信号弹正常发射要求。

6) 验证结果。将鱼雷放入水箱中, 当鱼雷处于自由稳定漂浮状态时, 测试漂浮姿态角约为9°, 头部浸水线基本位于雷头的中心, 这一实测结果与表1中计算值接近。实航发射试验中鱼雷航行终了后, 信号弹正常发射, 鱼雷正常回收。

5 结束语

本文针对鱼雷实航试验的安全回收, 开展了鱼雷航行终了漂浮姿态的分析研究, 对漂浮过程进行了详细分析, 找出了影响漂浮姿态的因素,给出了鱼雷漂浮姿态的工程计算方法, 并在鱼雷的实航试验中得到了验证。结果表明, 此方法可信、简洁、实用, 能够方便应用于鱼雷的工程设计和实航试验中, 可为鱼雷的总体结构布局、衡重参数设计、性能匹配计算、试验回收方案设计等提供参考依据, 并可推广应用于其他水下航行体的漂浮姿态计算中。

[1] 黄震中. 鱼雷总体设计[M]. 西安: 西北工业大学出版社, 1987.

[2] Unigraphics Solutions Inc. Unigraphics应用指导系列丛书[M]. 北京: 清华大学出版社, 2002.

(责任编辑: 陈 曦)

Analysis and Engineering Calculation of Torpedo Floating Attitude at Running End

ZENG Xiao-fan, CAI Wei-jun,XU Xin-dong,WANG Gai-di, BIAN Xiang

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Shanxi Pingyang Industry Machinery Co. Ltd., Houma 043002, China)

Successful recovery of a torpedo in sea trial is closely related to its floating attitude at running end. This paper proposes an intuitive and simple engineering calculation method of torpedo floating attitude at running end by analyzing the factors of influencing the floating attitude and the floating process. Sea trial verifies the correctness of the proposed engineering calculation method. This method can be simply applied to the torpedo design and sea trial, in terms of general structure layout, recovery plan, and match of balance weight parameters. This method can also be applied to the floating attitude calculation of other autonomous underwater vehicles.

torpedo; sea trial; floating attitude; engineering calculation method

TJ630.6

A

1673-1948(2014)05-0325-04

2014-03-06;

2014-05-22.

曾小凡(1980-), 男, 高级工程师, 主要研究方向为鱼雷总体结构.