微电机关键零部件尺寸偏差与性能偏差关系建模

潘跃林，张俊



微电机关键零部件尺寸偏差与性能偏差关系建模

潘跃林，张俊

(湘电集团股份有限公司特电事业部, 湖南湘潭 411101)

本文研究了微电机关键零部件尺寸偏差与性能偏差显性关系建模的方法，微电机关键零部件尺寸偏差与性能偏差之间关系模型很难用常规的方法建模，因此本文先采用泰勒展开方法建立微电机关键零部件尺寸偏差与性能偏差关系的显性数学模型，再运用Eviews进行回归分析，并对回归分析的结果进行分析研究，最终得到泰勒展开式的偏导系数，确定微电机关键零部件尺寸偏差与性能偏差关系的数学表达式。

微电机 尺寸偏差 性能偏差 泰勒展开 Eviews回归分析

0 引言

企业要想提高市场竞争力就必须提高产品关键零部件质量，而提高产品关键零部件的质量需根据其性能要求对关键零部件的关键尺寸公差合理控制[1]，为此研究产品零部件尺寸偏差与性能偏差的关系十分重要。有些产品关键零部尺寸偏差与性能偏差之间关系较为复杂，很难直接用常规的方法来求解，且产品关键零部件较多，要实现高维拟合难度较大，即使拟合出来精度也不会很高。本文采用泰勒展开式与回归分析方法建立产品关键零部件尺寸偏差与性能误差之间的关系模型，并以微电机为列验证了该方法的可行性。

1 关键零部件尺寸偏差与性能偏差关系的分析

微电机质量输出即空载电流1、空载转速2、负载电流3、负载电速4与其关键零部件的尺寸即铁芯高度1、轴的直径2、机壳内径3、后盖同轴度4、机壳同轴度5、换向器直径6有着一定的映射关系，但很难直接确定其显性数学表达式，因此先假设微电机性能与微电机关键零部件的尺寸的关系如1式所示。

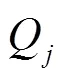
2 多元回归分析

采用多元回归分析的方法求解7式中的一阶偏导数与二阶偏导数，在Eviews软件[3]中分别对微电机四个性能偏差与关键零部件尺寸偏差的样本数据进行多次回归分析，剔除回归分析结果中的异常数据组，最后得到各性能偏差回归分析的检验概率、决定系数、修正决定系数、德宾-沃森检验值如下。

2.1 空载电流偏差回归模型

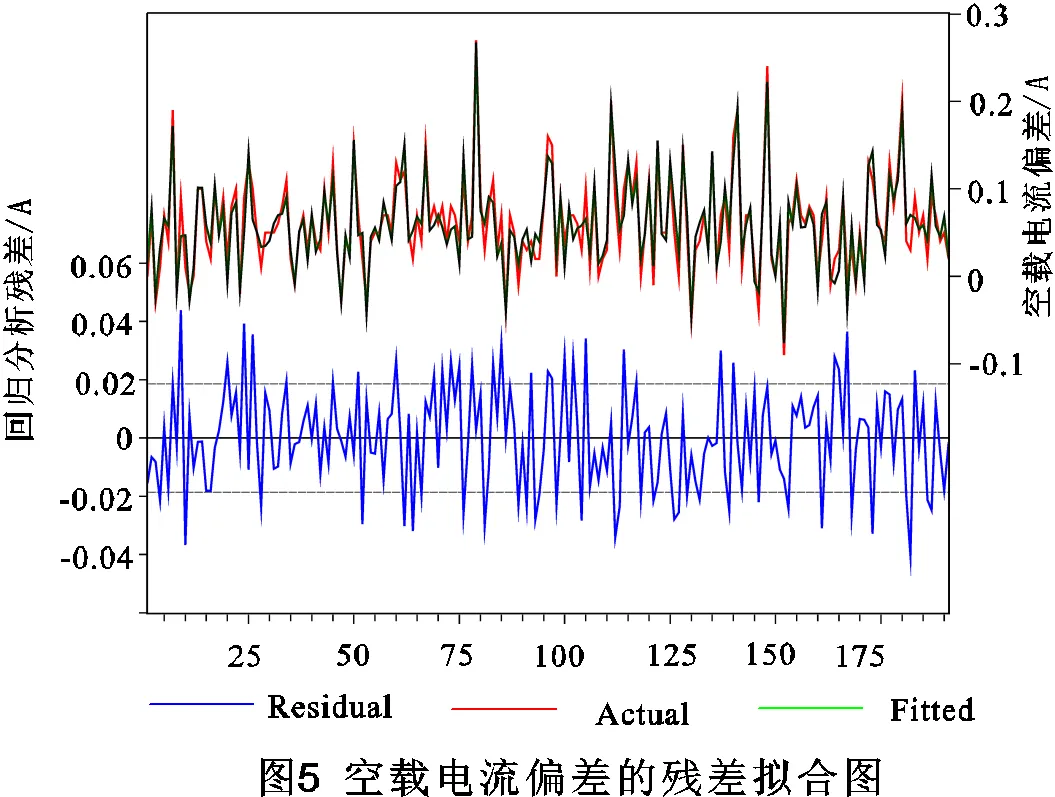
分析图1、表1可看出空载电流偏差回归模型的决定系数为0.852508，修正决定系数为0.825466说明自变量82.5466%的总离差平方和能被样本回归直线解释，因此空载电流偏差的回归直线对样本拟合程度较高；德宾-沃森检验值为2.311002，接近2，因此回归模型变量不存在序列自相关；27个待估计参数检验概率P中最大值0.0619比较小，且所有P接近0，因此均通过检验，说明空载电流回归模型具有很强的显著性，模型解释能力强。图5可看出空载电流偏差实际值与预测值的曲线基本吻合，且空载电流偏差的回归模型其残差值绝大部分在-0.02至0.02范围内。

图6可看出空载电流偏差回归模型的残差基本符合正态分布，残差最大值为0.043879，最小值为-0.040196。图7可看出空载电流偏差与回归模型残差平方没有固定规律，因此有空载电流偏差的回归模型不存在异方差性问题。

上述分析可知空载电流偏差回归模型较为理想，由回归分析可得微电机空载电流偏差与关键零件部尺寸偏差之间的数学表达式如8式所示。

2.2 空载转速偏差回归模型分析

图2、表1可知空载转速偏差回归模型的决定系数为0.891029，修正决定系数为0.886436，说明自变量88.6436%的总离差平方和能被样本回归直线解释，因此空载转速偏差的回归直线对样本拟合程度相当理想；德宾-沃森检验值为1.865217，接近2，因此回归模型变量不存在序列自相关；27个待估计参数的检验概率中最大值0.0692较小，且所有P值接近0，因此均通过检验，说明空载转速回归模型具有很强的显著性, 模型解释能力强。

图8可看出空载转速偏差实际值与预测值的曲线基本吻合，且空载转速偏差的回归模型其的残差值大部分在-30至30范围内。

图9为空载转速偏差残差的直方图，由图可知空载转速偏差回归模型的残差基本符合正态分布，残差最大值为50.83692，最小值为-54.58296。

图10可看出空载转速偏差与回归模型残差平方没有固定规律，因此有空载转速偏差回归模型不存在异方差性问题。

上述分析可知空载转速偏差回归模型较为理想，由回归分析可得微电机空载转速偏差与关键零件部尺寸偏差之间的数学表达式如9式所示。

2.3 负载电流偏差回归模型分析

图3、表1可知负载转速偏差回归模型的决定系数为0.863352，修正决定系数为0.841688，说明自变量84.1688%的总离差平方和能被样本回归直线解释，因此负载电流偏差的回归直线对样本拟合程度比较理想。德宾-沃森检验值为2.094273，接近2，因此回归模型变量不存在序列自相关；27个待估计参数的检验概率P中最大值0.0563较小，且所有P值接近0，因此均通过检验，说明负载转速偏差回归模型具有很强的显著性, 模型的解释能力强。

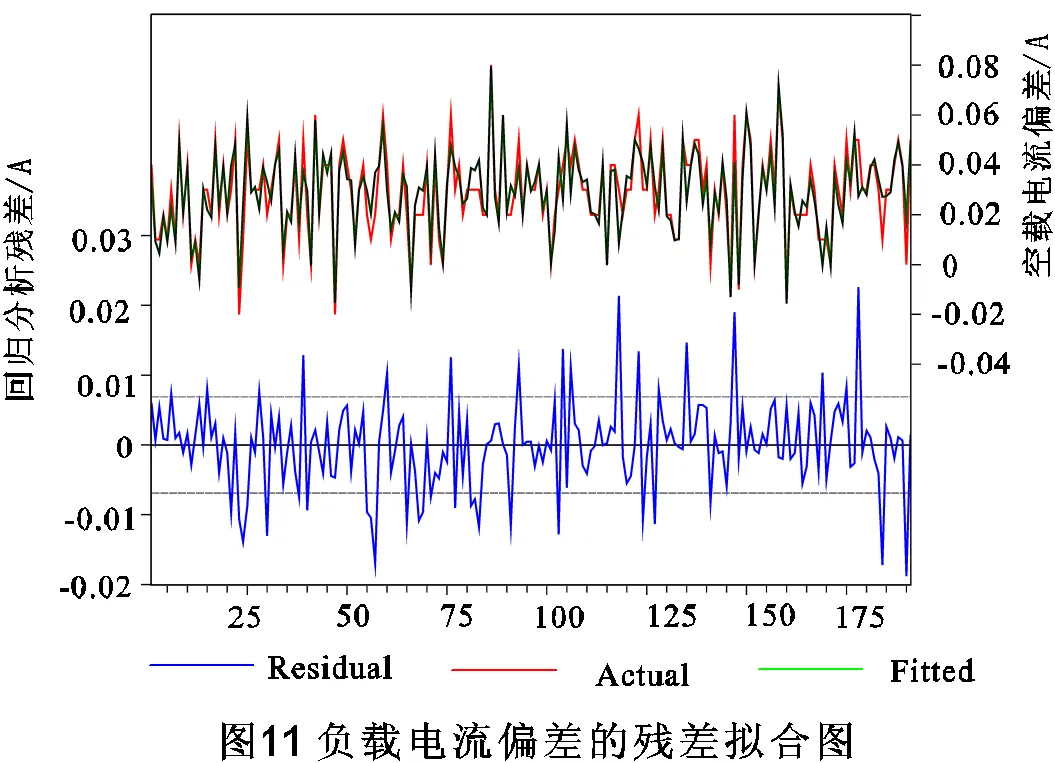
图11可看出负载电流偏差实际值与预测值的曲线基本吻合，且负载电流偏差回归模型的残差值大部分在-0.007至0.007范围内。

图12可看出负载电流偏差回归模型残差基本符合正态分布，残差最大值为0.02258，最小值为-0.018798。

图13可看出负载电流偏差与回归模型残差平方没有固定规律，因此有负载电流偏差回归模型不存在异方差性问题。上述分析可知负载电流偏差回归模型较为理想，由回归分析可得微电机负载电流偏差与其关键零件部尺寸偏差直接的数学表达式如10式所示。

2.4 负载转速偏差回归模型分析

由图4、表1可知负载转速偏差回归模型决定系数为0.898423，修正决定系数为0.883417，说明自变量88.3417%的总离差平方和能被样本回归直线解释，因此负载转速偏差的回归直线对样本的拟合程度较理想；德宾-沃森检验值为2.066249，接近2，因此回归模型变量不存在序列自相关；27个待估计参数的检验概率P中最大值0.0591较小，且所有P值接近0，因此均通过检验，说明负载转速偏差回归模型具有很强的显著性，模型的解释能力强。

图14可看出负载转速偏差实际值与预测值的曲线基本吻合，且负载转速偏差的回归模型的残差值大部分在-35至35范围内。

图15可看出负载转速偏差与回归模型残差平方没有固定规律，因此负载转速偏差回归模型不存在异方差性问题。

上述分析可知负载转速偏差回归模型较为理想，由回归分析可得微电机负载转速偏差与其关键零件部尺寸偏差之间的数学表达式如11式所示。

3 结论

本文研究了微电机关键零部件尺寸偏差与性能偏差关系建模的方法，微电机关键零部件尺寸偏差与性能偏差之间关系非常复杂，因此采用泰勒展开方法建立微电机关键零部件尺寸偏差与性能偏差关系的数学模型，运用回归分析方法计算出泰勒展开式的偏导数，并对回归模型拟合情况分析，最后确定微电机关键零部件尺寸偏差与性能偏差关系的数学表达式。

[1] 吴昭同,余忠华,陈文华.保质设计[M].北京:机械工业出版社,2004.

[2] BEYER H G, SENDHOFF B. Robust optimization a comprehensive survey [J].Computer Methods in Applied Mechanics and Engineering, 2007, 196(33):3190-3218.

[3] 攸频,张晓峒. Eviews 6实用教程[M]. 北京:中国财经出版社, 2008.

Modeling of Key Parts Dimension Deviation and Performance Deviation for Micro-motor

Pan Yuelin, Zhang Jun

（Xiangtan Electric Group Co. Ltd, Xiangtan 411101, Hunan,China）

TM382

A

1003-4862（2014）07-0075-06

2014-05-17

潘跃林（1977-），男，工程师。研究方向：电机。