顺学而教,在“存异”中“求同”
——以解决问题的策略(假设)为例
杨金珠
(南京市江宁实验小学,江苏南京,211106)
苏教版六(上)解决问题的策略(假设)是在学生已经学习了画图、列表、一一列举和倒推等策略基础上又一次有关策略的学习,许多课外辅导用书和提优训练都把此类问题称之为“鸡兔同笼”。解决此类问题需要学生具备较高的思维水平和逻辑推理能力。
一、了解学生学习情况
为了全面掌握学生知识情况,笔者课前对所教两个班级103名学生进行“学习前置”(只做“自主探索”部分)。
表1学生预习表

课题解决问题的策略(2)自主探索 例2:全班42人去公园划船,一共租了10只船。每只大船坐5人,每只小船坐3人。租用的大船和小船各有多少只?想一想:你能用已学过的策略解决这个问题吗?
结果统计如表2。

表2 学生预习情况统计
从上表信息可知:学生想到用列表方法(含多种方法中的列表)解决的有50人,占49%;画图9人,占8.7%;算式54人,占52.4%;方程14人,占13.6%。通过分析能看出学生解决此类问题时所使用的一般方法是列表法和假设法。接着,笔者对学生做了进一步调查。
师:你是怎么想到用这些方法的?
生1:我们在五年级学过一一列举,这道题目数字不大,我一个一个列出来就能找到答案了。
生2:画图的方法比较直观,好理解。
生3:这学期第一单元我们学的就是方程,根据等量关系就可以列出方程,不过怎样解方程是我爸爸教的。
生4:我在辅导班的时候学过用假设法求解。
师:对于用假设法列出的算式你能解释每一步表示的意义吗?
生4:我只是记住算式模型。
通过访谈,可以较客观地了解到学生对于此类问题的一般思考过程和个体间的思维差异。教学中要尊重这种差异,充分展示彼此间不同的观点和想法,在多维立体互动中不断对学生差异进行比较、修正和提升。而这,无疑是需要教师进行思考和正视的。
二、教学案例分析
(一)列表
1.陈诺:我先从9只大船1只小船开始想。9只大船1只小船可以坐50人,比42人多,8只大船2只小船……
生1:当我们列举出“6只大船4只小船”正好坐42人时,下面就不要再列举了。因为随着大船的增加,小船的减少,人数会越来越多,肯定不符合条件。
师:对于这张表格的数据同学们有什么发现?
生2:每增加1只大船,减少1只小船,人数会多2人。
生3:我补充一下,应该有个条件“船的只数10只”要保持不变。

一一列举是学生以前学过的策略,这其中就蕴含了“假设”的思想,学生通过同学对列表方法的介绍,初步体会“假设”思想在列表中的运用。同时,与以前所学的一一列举答案的多样性不同,此类题目答案是唯一的。
师:我觉得应该从“10只大船0只小船”开始想。虽然“10只大船和0只小船”一看就知道不符合条件,但如果写出来的话,这样列表就会很有序。
(用红笔补上“10只大船0只小船”)
假设策略的重心是假设后的调整,调整的过程实质上是替换的过程。在“一一列举”中其实就蕴含“一一替换(1只小船替换1只大船)”的思想。当教师提出需要补上“10只大船0只小船”时,“10大0小”或“0大10小”正是下面学生画图、假设法的基础,这样从学生熟知的列表法切入符合学生的实际。
2.唐沛年:我和陈诺的方法有点不一样,我是从1只大船9只小船开始想的……
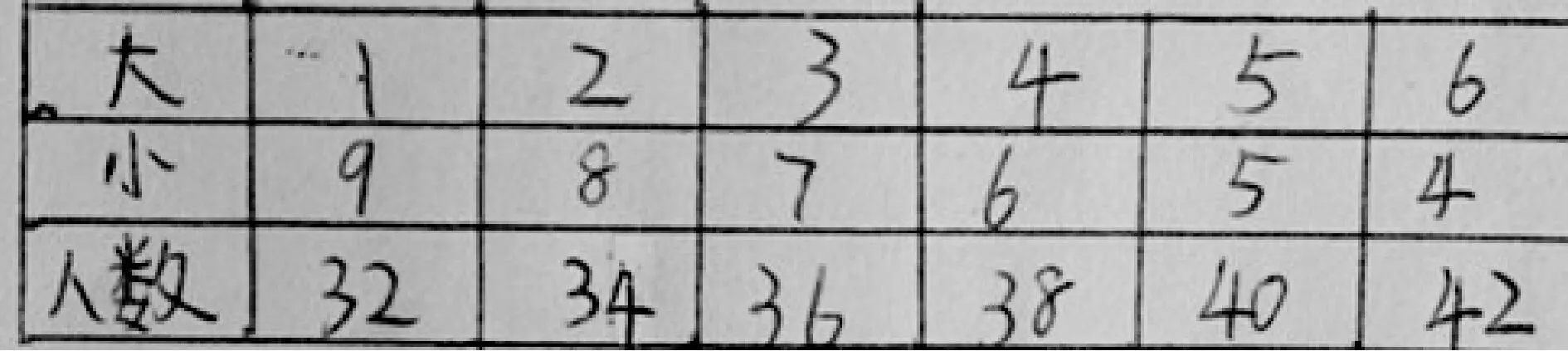
生1:我发现陈诺列举的次数多。
师:你能解释其中的原因吗?
生1:当我们假设9只大船1只小船时,总人数是48人,48离42很近。而1只大船和9只小船总人数是32人,离42比较远。
生2:有价值的发现!如果从不同的角度思考,替换次数会有不同。
生3:应该像陈诺那样补上“0只大船和10只小船”的情况。
设计意图:学生两种不同的列表方法实际上就是两种不同假设法的原型。在这里通过师生对话、生生互动,为下面调整假设策略解决问题做了提前渗透和有力铺垫,可谓“未成曲调先有情”。
3.岳晨曦:我先假设有5只大船和5只小船,可以坐40人,然后4只大船6只小船发现人数少得更多,所以应该是6只大船4只小船。
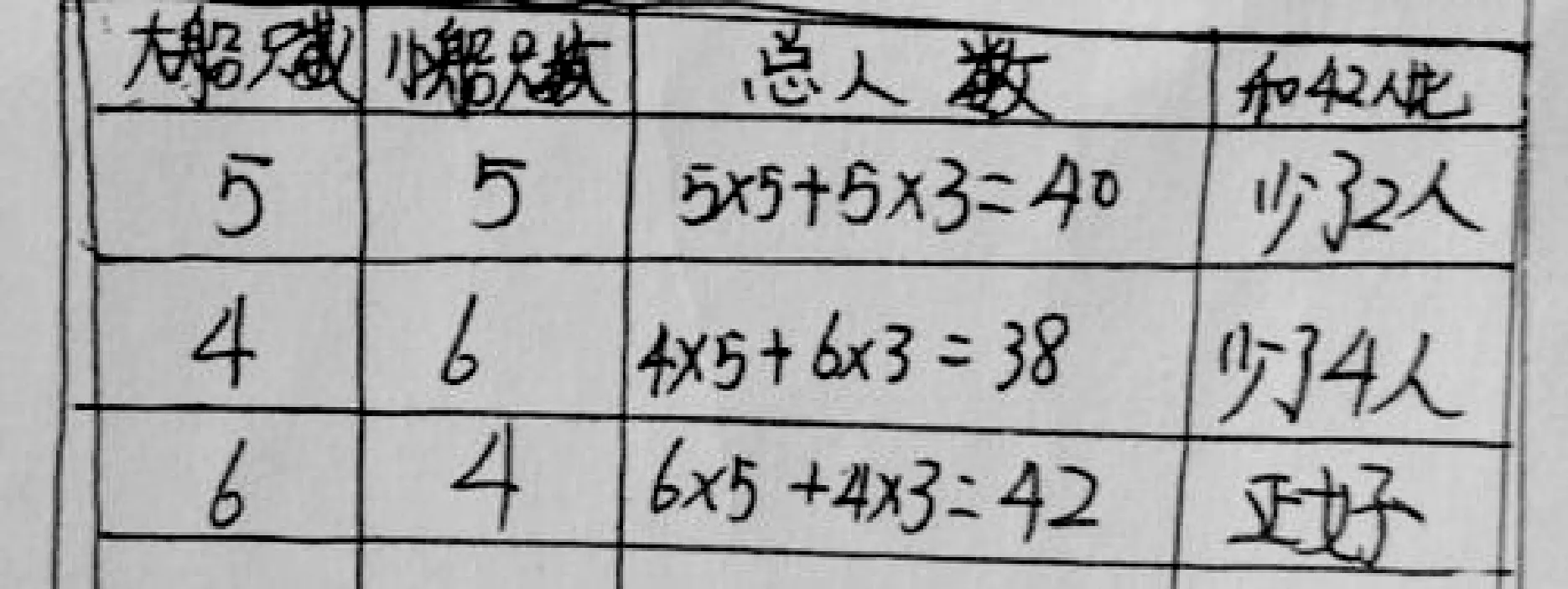
师:是的,当岳晨曦先假设“5大5小”时发现和42人是有“差距”的,岳晨曦先用向小船方向调整,发现人数少更多,所以才向大船方向调整,谁能解释其中的道理?
一股透骨的寒气直抵他的心底里,他不禁打了一个寒颤。莫非……他不敢继续想下去了,那简直太可怕了!还没有弄清事实的真相,一股巨大的忧郁就将他彻底地击伤了,他默不作声,离开了茶庄。山野中移动着一个越来越小的灰点,像一朵灰暗的流云在缓慢地往山坡下飘移。冷飕飕地刮来一阵凉风,他突然感到满目疮痍的荒凉,身子也失重似的飘浮起来。以往,他喜欢独来独往,喜欢独自在山野里漫步,享受那份清静,那种自在,孤独与快乐。可是眼下,他像一个幽灵似的在荒山野岭里飘荡着,红尘世界里,他只能是一只小小的蝼蚁。佛在云端拈花微笑,是否见到了他这枚枯黄的落叶在风中飘动?
生:当5只大船5只小船时坐40人,比42人少,所以应该增加大船减少小船,因为大船能坐更多的人。
设计意图:调整可以是“渐进式”的,也可以是“跨越式”的,无论从哪个角度想起,重点都是要让学生借助表格感受为什么要把大船换成小船或者为什么要把小船换成大船,以及因为“换”而带来的人数变化。充分展开这个过程,使学生深刻体会调整的目的、方向和方法,进而初步形成调整意识。
(二)画图
陶致远讲解画图过程。

师:陶致远为什么一次只画去2人?
生:一只小船替换一只大船只能少2人。
师:谁能把陶致远和陈诺的方法联系来说一说?
设计意图:借助图示,结合学生的讲解把结果的呈现过程化、动态化,清晰呈现画图过程。并与列表方法相互比较,相互验证,相互启迪。这其中算式方法的雏形已初见端倪,使学生对假设策略的认识进一步接近其核心和本质。
(三)算式
蒋霏凡介绍自己的思考过程。
师:同学们,“数形结合”是一种重要的思想方法,你能不能根据陶致远的“图”来解释这位同学的算式呢?

设计意图:细细分析列表、画图和算式,可以发现都有假设和替换的影子。某些时候,它们的思路完全一致。“打通”这些方法的联系,让学生通过不同的方式理解同一种策略,理解会更深刻。
师:明明假设的全是大船,怎么求出来的却是小船呢?
(学生一时难以回答,沉默片刻后,从画图方法中找到了解释)
生1:因为假设全是大船,会多算出8人。
生2:把多算的8人要“赶下船”,1只大船“赶”下两人后就变成小船,因为要“赶”4次,就变成了小船。所以假设全是大船,求出来的就是小船。
生3:如果假设全是小船,求出来的就是大船。
设计意图:为什么明明假设的是大船,求出来的却是小船?这历来是不少学生的困惑之处。在这里,教师应放大这个环节,在反问、追问中,放慢进程,借助表格的直观、示意图的支撑、形成式的凝练,理解掌握假设法的内涵和本质,在此基础上抽象出一般算式方法。
三、分析总结
通过列表和画图不难发现,随着小船数量的逐一增加,总人数逐次减少2人,正是这一基本的变化规律,我们很容易得出“如果人数要减少2人,应该将一只大船‘变成’小船,反之,人数要增加2人,应该将1只小船‘变成’1只大船”。进而思考:如果人数要减少8人(增加12人),应该将几只大船(小船)“变成”几只小船(大船)?有了这些观察思考的基础,在列表和画图中就找到了“假设法”的影子。如果说第一次列举被视为假设的前提,那么接下来就可以根据人数的差距,计算出应该将多少只大船(小船)“变成”小船(大船),就能解决一共有多少只大船和多少只小船的问题。由此,解决“鸡兔同笼”一类问题的典型方法——假设法,便跃然纸上。这样教学不仅切合教材的实际,而且切合教学的实际,更是切合学生的实际。
[1] 周胜琼.小学数学六年级上册“鸡兔同笼”教学反思[J].中国科教创新导刊,2012(6).
[2] 潘粉娥.“鸡兔同笼问题”教学设计[J].课程教材教学研究:小教研究,2013(12).
[3] 王兴.浅谈如何提高小学六年级数学的教学质量[J].教育教学论坛,2013(11).

