嫦娥三号软着陆轨道与最优控制器设计
俞丁丁,金杨杰,张励冠,夏志乐
(台州学院 数学与信息工程学院,浙江 临海 317000)
嫦娥三号软着陆轨道与最优控制器设计
俞丁丁,金杨杰,张励冠,夏志乐*
(台州学院 数学与信息工程学院,浙江 临海 317000)
以软着陆于地形较为复杂的月球预定区域为背景,研究了高速运行嫦娥三号的着陆轨道与控制策略的设计问题。以燃料消耗最省为设计指标,根据Pontryagin极大值原理,给出了耗损燃料的最优推力方案,设计了相应的着陆轨道和六个阶段的最优控制器,结合迭代法进行各个阶段的模拟仿真,最后对误差和敏感性进行详细的分析。
嫦娥三号软着陆;最优控制;迭代法;Pontryagin极大值原理;
嫦娥三号是继美国、前苏联实施无人月球软着陆后由中国发射的第一个地外软着陆探测器和巡视器,与之前的一号、二号相比更是突破了月球软着陆、月面巡视等关键技术。在选择着陆区域的问题上采取对几种基本要求进行指标打分的方式,最后确定虹湾区作为着陆区。
由于月球上没有大气,嫦娥三号无法依靠降落伞着陆,只能靠变推力发动机才能完成中途修正、近月制动、动力下降、悬停段等软着陆任务,因此设计出一条轨道路线在保证安全的情况下达到燃料消耗最省显得尤为关键。
相关学者对此进行了研究,孙军伟[1]等通过将常推力的月球软着陆轨道优化问题转化为一个多参数优化问题,由逐次二次规划算法得到了最优解。本文在相关研究的基础上,进一步分析和实现了软着陆的具体方案和过程,满足了轨道设计的基本要求,并以燃料消耗最省为设计指标,设计了相应的着陆轨道和六个阶段的最优控制器,同时对误差和敏感性进行详细的分析,是对上述优化问题的细化和补充。
本文主要讨论以下问题:
问1.确定着陆准备轨道近月点和远月点的经纬坐标,以及嫦娥三号相应速度的大小与方向。
问2.确定嫦娥三号的在每个阶段的着陆轨道和在6个阶段的最优控制策略。
问3.对于问题二的模型做相应的误差分析和敏感性分析。
本文数据来源于2014年全国大学生数学建模竞赛A题。
1 问题分析
1.1 问题一分析
首先我们需要确定轨道设计的基本要求,在明确这个要求以后利用物理学、力学、数学等相关知识建立相应的数学模型,再进行编程检验所建立的数学模型,确保嫦娥三号下一阶段的着陆能顺利完成。
1.2 问题二分析
我们对每一个阶段进行分析,对于主减速阶段我们在问题一中已经解决;对于快速调整段,我们要保
证下降到2 400m的时候水平方向的速度减为0,如果在未到达2 400m的时候就已经使得水平方向的速度为0,那么我们只需要让它在竖直方向上下降到2 400m即可;如果在到达2 400m的时候能同时保证水平速度为0,那就让它以这个轨迹下落;对于粗、精避障段,由于要避开大陨石坑,我们应先对已知的图像进行处理,通过观察,如果它开始就不落在大的陨石坑中,那么就按照原来的那个轨迹继续下落;如果它刚开始的中心就已经在大的陨石坑中,那我们要调整它水平方向上的位移,使得它能落到相对较平的表面;对于缓速下降段,我们只需将到达4m处的竖直速度变为0然后又再进行自由落体运动即可。
1.3 问题三分析
模型的建立应该考虑检验的原理如误差计算公式,敏感性的表达式。误差分析的切入点在于比较计算值与实际值的比较,敏感性分析的出发点是对参数本身的质疑,如果给参数一定浮动但对于目标值的影响不大,则能侧面验证被检验模型的普适性高。处理方式可由计算公式得到对应值,或作图直接分析。
2 模型建立
2.1 椭圆轨道运动速度模型
文献[2]中指出行星在环绕椭圆轨道运动中,速度每时每刻都在变化,而瞬时速度的平方,等于引力常数与中心天体质量及半焦弦的积,除以主星中心与行星中心连线距离的平方。
2.2 霍曼转移准备着陆轨道模型

图1 准备着陆轨道分析图
嫦娥三号准备着陆时的运动如图1所示,在运行轨道半径为r_1的圆形近月轨道上,在远月点收到变轨指令,发动机点火加速,由圆轨道进入霍曼转移轨道,而轨道上物体的总能等于动能与重力位能的和,而总能又等于重力位能(轨道半径为轨道半长轴a时的重力位能)的一半,
其中:v为物体的速度;μ=GM为中央物体的标准重力参数;r为物体至中央物体中心距离;a为物体轨道的半长轴。
r1,r2分别是原本圆轨道与目标轨道的半径,其中大的(小的)对应到霍曼转移轨道的远拱点(近拱点)
的距离。
2.3 平面月球二维动力学模型
2.3.1 各阶段下降过程中的受力运动过程分析
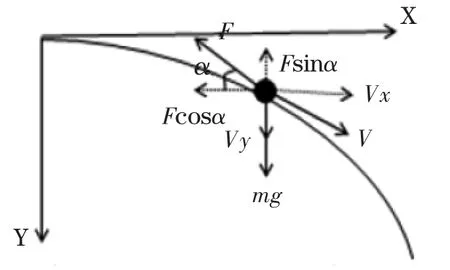
图2 主减速段受力分析图
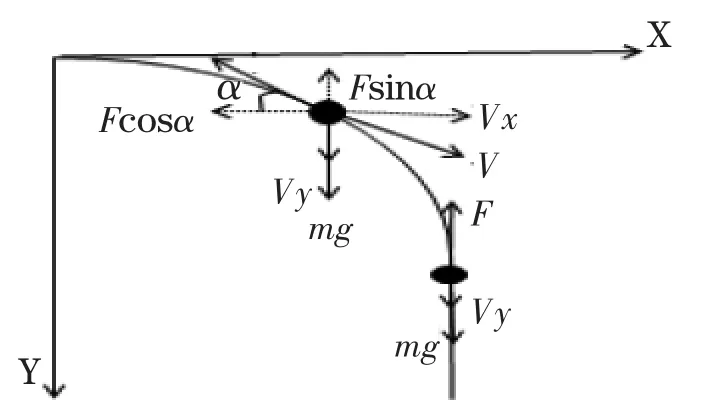
图3 快速调整段受力分析
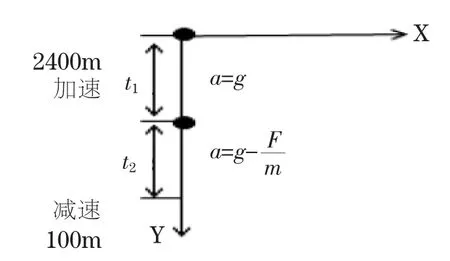
图4 粗避障段运动过程分析

图5 精避障段受力分析
2.3.2 主减速段动力学模型
由于准备着陆的速度方向是平行于月球表面的,因此开始的竖直方向的速度为0,而水平的速度为近月点的速度,如图2所示,建立以下微分方程组:

2.3.3 快速调整段动力学模型
我们先将主减速阶段进行延续,如图3所示,建立重力转弯软着陆[3]的微分方程模型:

考虑到当水平方向的速度将为0时,竖直的位移并没有到达2 400m处,因此我们再建立竖直方向上的匀减速模型:

2.3.4 粗避障段动力学模型
由上一阶段可以得到在2 400m的时候的速度为10.83m/s,若在这一阶段一直做减速运动,这样就一直有推力的作用从而使得燃料消耗的过多;若在这一阶段开始不用推力的作用,使得到达一个点之后再进行匀速最后在减速,这样在匀速的阶段同样也会有多余的燃料消耗;若我们没有匀速这一阶段,那么推力的作用只在减速的时间段内进行,这样会让燃料减小的最少。如图4所示。对先加速后减速阶段建立垂直动力学模型[4]:

2.3.5 精避障段动力学模型
为了使得在30m的时候水平方向速度又降为0,因此,我们应该让得出来的水平方向要移动距离的前半段在加速,通过控制前后的推力相等,每时刻角度的大小相等,就能保证后半段将速度减为0的同时刚好达到30m处。如图5所示。
于是我们建立微分方程组:
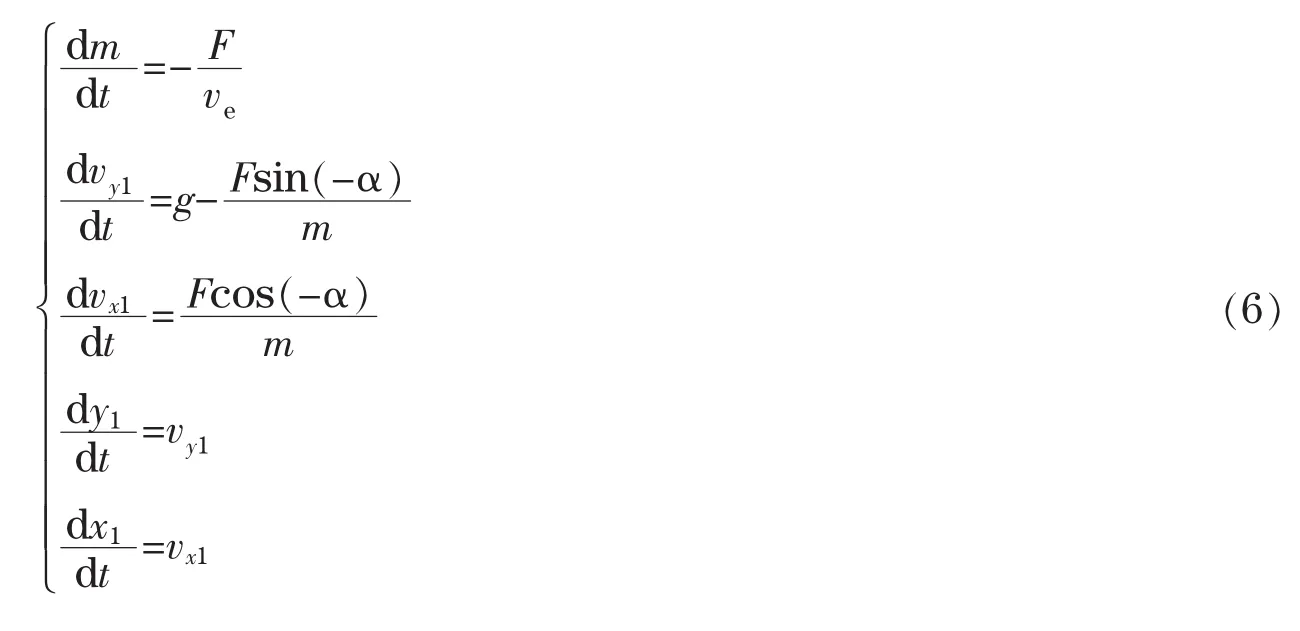

并且控制

2.4 缓速下降段垂直动力学模型
根据文献[5]中,在该段中,着陆器离月面很近,且着陆器几乎沿着竖直方向下降。于是对该阶段进行分析,见图6。
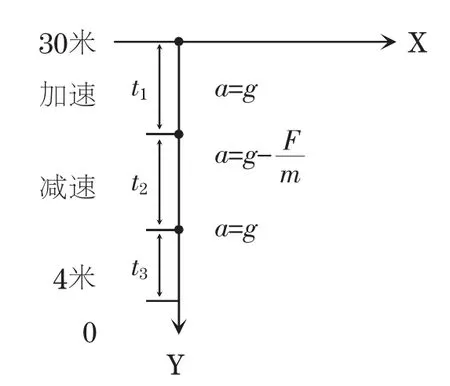
图6 缓速下降段运动过程分析
对先加速后减速再自由落体阶段建立垂直动力学模型:
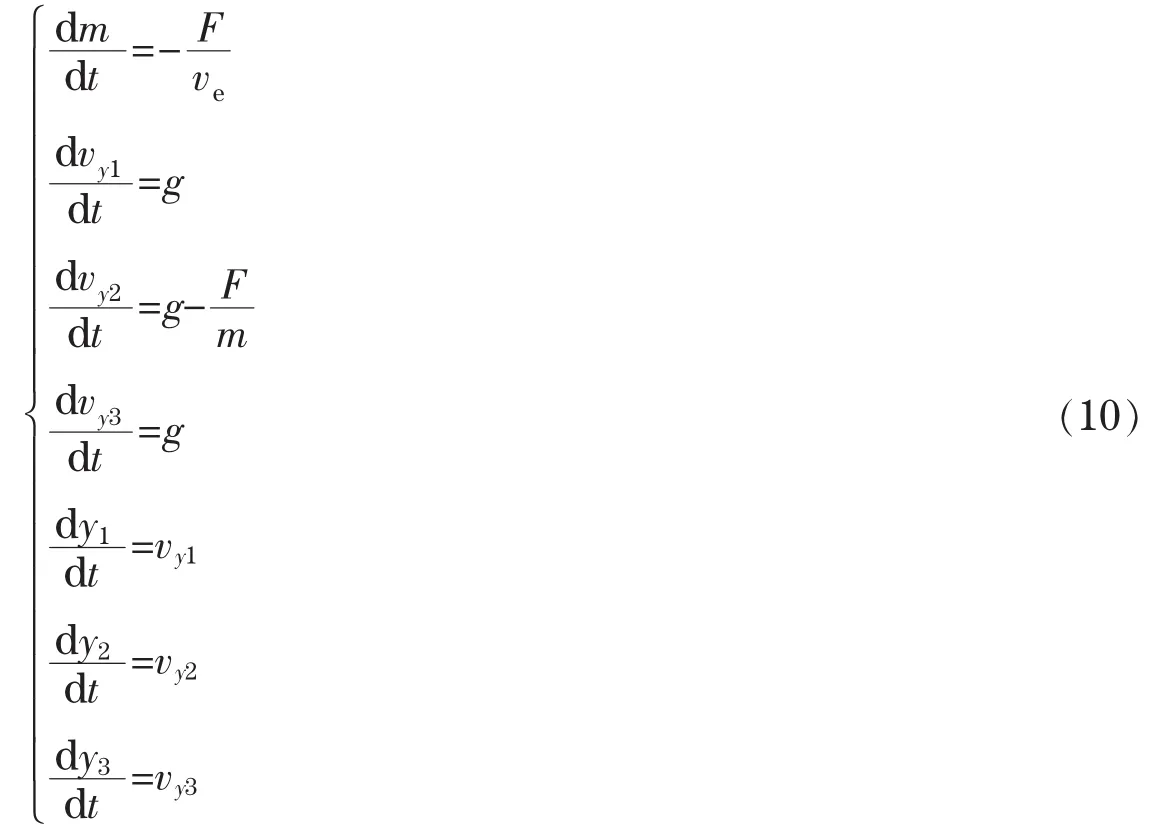
而自由落体阶段我们只需要建立运动公式

3 Pontryagin极大值原理求解
令状态向量X=[m,Vy,Vx,y,x]^T,非线性函数.
假定初始时刻t0=0,终端时刻tf自由,则软着陆的初始条件由探测在近月点的状态确定,而m(0)=m0,Vx=1665.184m/s,Vy=0,y0=15km,x0=0.
为了确保下一阶段着陆能顺利实施,需要加上终端条件y(tf)=3km,vy(tf)=57m/s,

应用Pontryagin极大值原理,取终端性能指标为:J=φ[X(tf)]=m0-mtf.
构造哈密顿函数为:H(x,λ,F)=λT.f
其中λ=[λm,λVy,λVx,λy,λx]T.满足
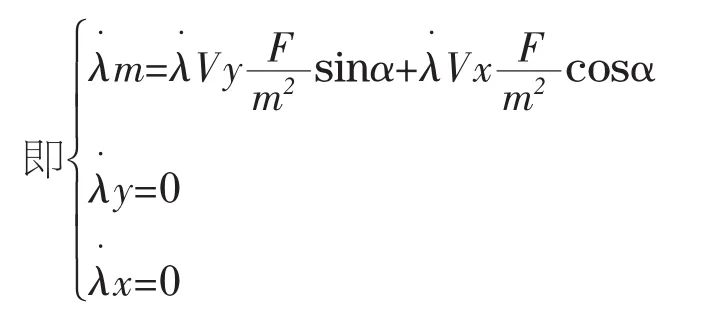
根据Pontryagin极大值原理,得最优推力为:
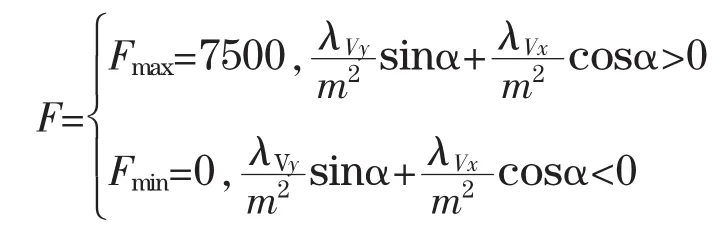
4 仿真分析
首先给出计算的初始条件,嫦娥三号在着陆准备轨道上的运行质量为2.4t,其安装在下部的主减速发动机能够产生1 500N到7 500N的可调节推力,其比冲(即单位质量的推进剂产生的推力)为2 940m/s。着陆准备轨道为近月点15km,远月点100km的椭圆形轨道。主减速段的区间是距离月面15km到3km,实现到距离月面3km处嫦娥三号的速度降到57m/s。快速调整段需要从距离月面3km到2.4km处将水平速度减为0m/s。粗避障段是距离月面2.4km到100m,要求避开大的陨石坑,并初步确定落月地点。精细避障段的区间是距离月面100m到30m,确定最佳着陆地点,实现在着陆点上方30m处水平方向速度为0m/s。缓速下降阶段是距离月面30m到4m,要求在距离月面4m处的速度为0m/s,即使现在距离月面4m处相对月面静止,之后关闭发动机,使嫦娥三号自由落体到精确有落月点。对已知的数据进行仿真,结果见图7~9。
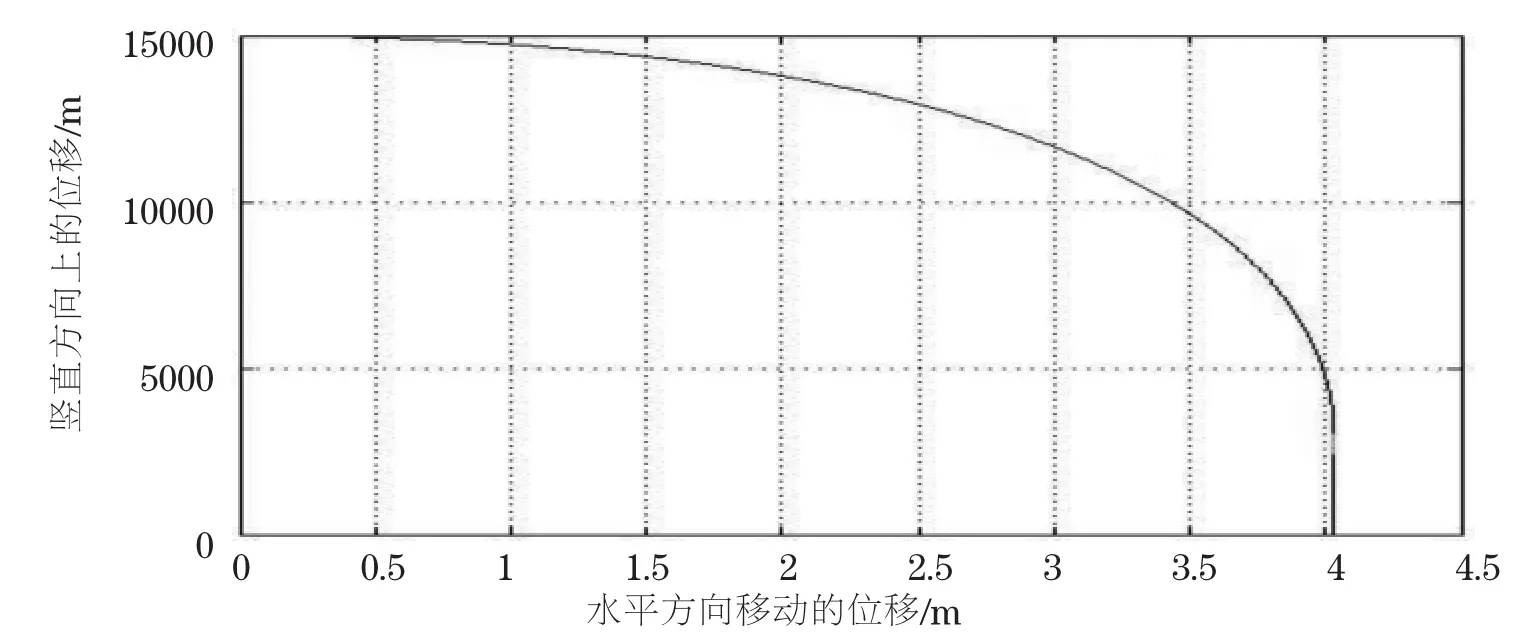
图7 嫦娥三号软着陆全过程轨迹图
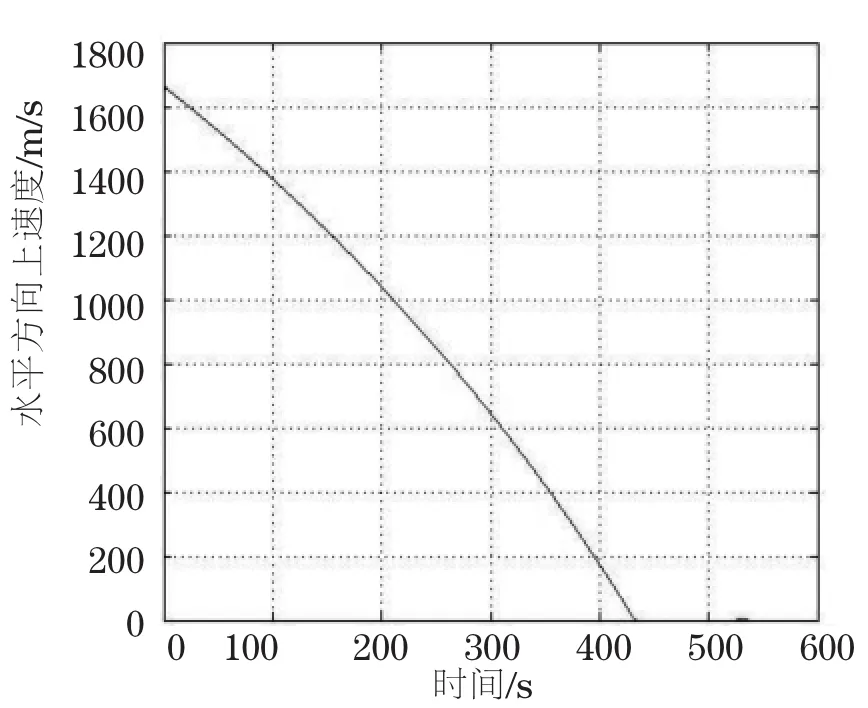
图8 全过程嫦娥三号水平方向速度随时间变化
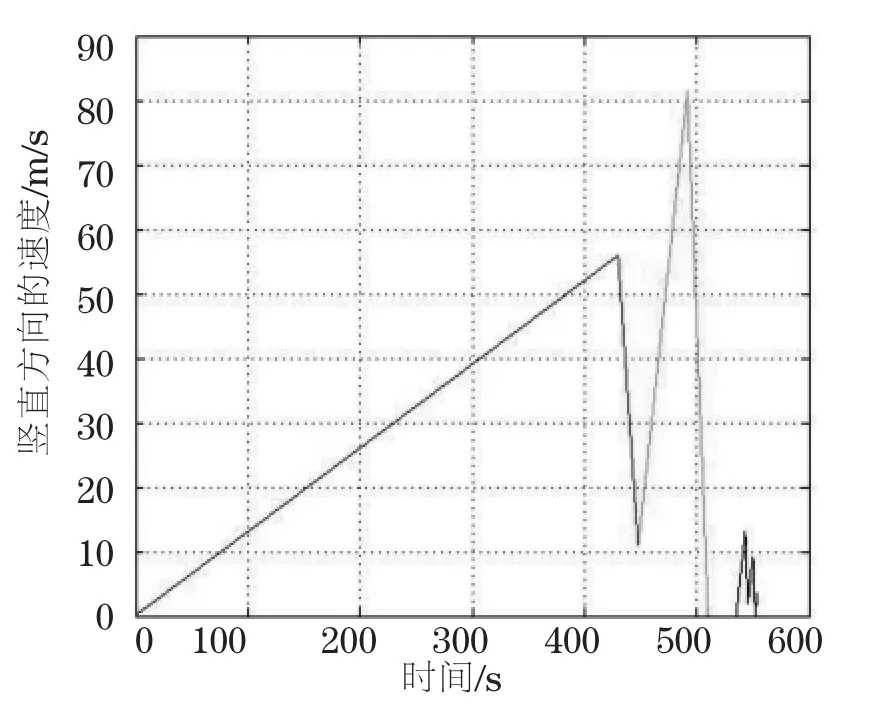
图9 全过程嫦娥三号竖直方向速度随时间变化
5 灵敏度分析
采取参数小波上下浮动得到表1和图10、图11。

表1 误差分析表
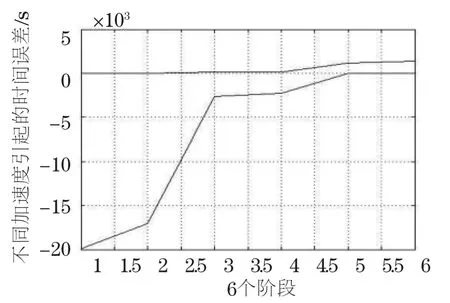
图10 不同参数下的灵敏度分析图
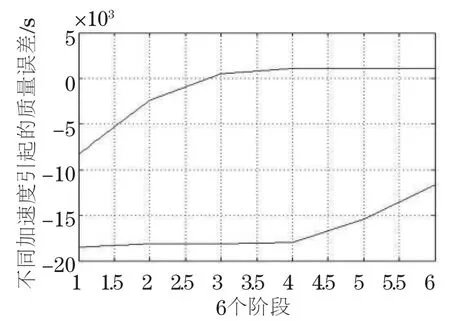
图11 不同参数下的灵敏度分析图
6 模型推广
1)本模型用了迭代法来解决很难求解的微分方程组,可以运用到各式各样的微分方程组中,以牺牲部分精度来求解方程。
2)本文的模型是软着陆模型,因此可以推广至各表面无大气的星球中,只需要改变一些参数即可。
3)对于本文的微分方程模型我们可以结合文献[6],考虑用蚁群算法来求解。
7 结论
嫦娥三号在软着陆的过程中,通过调整姿态、减速、悬停等一系列机动过程,使得在落月段的轨迹变得较为复杂。本文对各阶段进行动力分析,通过建立相应的微分方程模型,进行经纬度确定,最后得出的结果为嫦娥三号在近月点以1 665.184m/s的速度,平行于月球表面进行降落,在主减速段进行429.9s,水平方向移动403.293km。然后继续降落,在快速调整段进行18s,继续粗避障段,进行62.24s后进行悬停,再在精避障段进行35.42s,最后缓速阶段进行8.8s后得以降落到月球表面。总共历时551.36s,与实际较相符合。
[1]孙军伟,乔栋,崔平远.基于SQP方法的常推力月球软着陆轨道优化方法[J].宇航学报,2006,27(1):99-102.
[2]李亚平.椭圆运动与圆运动的统一[J].科技信息,2010(1):422-424.
[3]蔡艳芳.月球探测器软着陆制导方法研究[D].西安:西北工业大学,2006.
[4]单永正,段广仁.应用非线性规划求解月球探测器软着陆最优控制问题[C].哈尔滨工业大学控制理论与制导技术研究中心,2007.
[5]王鹏基,张熇,曲广吉.月球软着陆飞行动力学和制导控制建模与仿真[J].中国学,2009,39(3):521-527.
[6]段佳佳,徐世杰,朱建丰.基于蚁群算法的月球软着陆轨迹优化[J].宇航学报,2008,29(2):476-481.
Chang E III's Soft Landing Trajectory and the Optimal Controller Design
YU Ding-ding,JIN Yang-jie,ZHANG Li-guan,XIA Zhi-Le*
(School of Mathematics and Information Engineering,Taizhou University,Iinhai 317000,China)
To set a soft landing in the complex terrain predetermined area of the moon's prospective region as background,we studied the high-speed operation Chang E III's design problems of the landing track and control strategy.With fuel consumption the most provinces as design index,according to the Pontryagin maximum principle,not only fuel consumption optimal thrust scheme was given, but also the corresponding landing orbit and six stages of optimal controller were designed. In addition,each phase of the simulation were combined with iterative method.finally,we provided a detailed analysis of the sensitivity and error.
Chang E III's soft landing;the optimal control;iterative-method;the Pontryagin maximum principle
10.13853/j.cnki.issn.1672-3708.2014.06.004
(责任编辑:耿继祥)
2014-11-06;
2014-11-27
简介:夏志乐(1979- ),男,江苏连云港人,讲师,硕士,主要从事运筹学与控制论研究。

