滚转导弹过载驾驶仪控制耦合解耦算法研究

宋韬，林德福，魏志军，李川

(1. 北京理工大学 宇航学院，北京100081;2. 第二炮兵装备研究院，北京100085)

0 引言

滚转导弹由于弹体绕纵轴旋转，其俯仰偏航通道存在一定程度的耦合，包括气动耦合、测量耦合和控制耦合等［1-3］。当舵机控制指令被弹体转速调制后，舵控频率增加，从而对舵机频带提出了更高的要求，因此由舵机频带约束导致的控制耦合常常限制了过载驾驶仪在滚转导弹上的应用［4-5］。目前，国内外尚未有过载驾驶仪在滚转导弹成熟型号上成功应用的先例。

随着制导控制技术的发展，滚转导弹应用范围逐渐向高速、强机动、大空域方面扩展，过载驾驶仪在滚转导弹上的应用问题正在逐渐引起关注。国内外部分学者［5-6］尝试过将经典俯仰偏航通道独立的驾驶仪设计方法扩展到滚转导弹驾驶仪设计工作中，但由于未考虑耦合，难以保证驾驶仪稳定。袁天保［7］、Fortescue 等［8］采用多变量频域分析方法将经典的单变量频域分析方法扩展到多输入舵输出系统中，利用对角优势化方法设计了动态补偿矩阵，实现控制耦合的近似解耦，但解耦效果受弹体转速波动的影响较大。陈罗婧等［9］利用前馈补偿方法进行解耦，但解耦算法需要已知导弹飞行速度、飞行高度及转速等信息，难以实现工程应用。

本文分析了舵机动力学滞后引起的滚转导弹驾驶仪控制耦合问题，提出了一种滚转导弹舵机频带指标的工程设计思路，并对比研究了基于最优舵面超前角度补偿解耦和输出反馈的动态解耦2 种方法。最后，通过仿真验证了解耦方法的可行性。

1 滚转导弹驾驶仪模型

轴对称的双通道控制滚转导弹后视图如图1 所示。

图1中:y 轴和z 轴分别为准弹体系俯仰轴和偏航轴;yb和zb分别为弹体系俯仰轴和偏航轴;Iyb轴、Izb轴为惯性器件2 个敏感轴;δyb和δzb分别为弹体系下俯仰舵转角和偏航舵转角;δy和δz分别为准弹体系下俯仰舵转角和偏航舵转角;ωx为弹体转速。

考虑控制耦合时，滚转导弹驾驶仪俯仰和偏航通道不独立，为一个双输入双输出系统如图2 所示。

图2中:ayc和azc分别为准弹体系下俯仰过载指令和偏航过载指令;aybc和azbc分别为弹体系下俯仰过载指令和偏航过载指令;δybc和δzbc分别为弹体系下俯仰舵指令和偏航舵指令;ay和az分别为准弹体系下俯仰过载输出和偏航过载输出;ayb和azb分别为弹体系下俯仰过载输出和偏航过载输出;Gs为舵机;Y1为弹体;Y2为惯性器件。

由图2 可知，弹体系下俯仰和偏航舵机指令为

式中:

由于惯性器件带宽远大于驾驶仪闭环带宽，因此Y2的动力学可由常值增益表示，(1)式可等效为

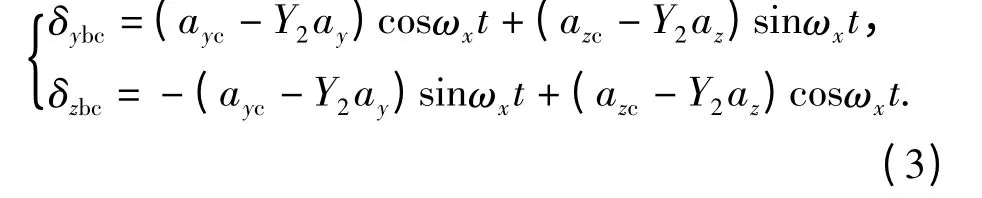
由(3)式可知，滚转导弹过载驾驶仪可等效为准弹体坐标系下的反馈回路，如图3 所示。

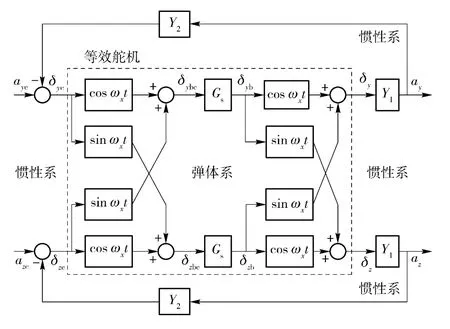
图3 滚转导弹过载驾驶仪等效框图Fig.3 Equivalent block diagram of the spinning missile autopilot

图3中:等效舵机的输入和输出分别为舵指令δyc、δzc和舵转角δy、δz. 等效舵机反映了舵机动力学滞后引起的控制耦合问题。

2 等效舵机分析

设舵机动力学传函为Gs(s)=1/(Tss +1)，舵机带宽ωs=1/Ts. 利用频率响应的方法对等效舵机进行分析。

1)设准弹体系下舵指令输入δyc=sinωt、δzc=0，此时弹体系下舵指令δybc和δzbc分别为

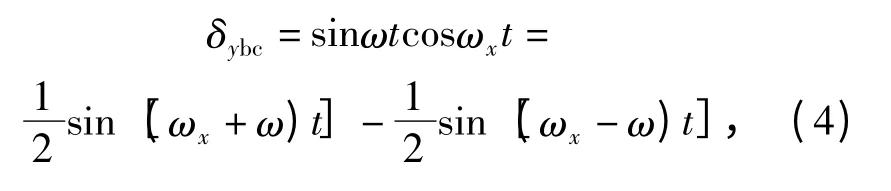
频率为ωx+ω 和ωx-ω 的信号经过舵机动力学后幅值分别为原信号的A1倍和A2倍，相位分别滞后φ1和φ2:

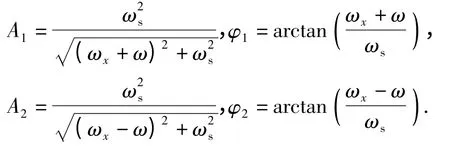
因此弹体系下舵机输出δyb和δzb可表示为

向准弹体系投影，得到准弹体系下舵机输出

式中:

定义 G11(s)=δy/δyc，G11(s)的频率特性可由幅值Km和相位θm表示。

定义 G21(s)=δz/δyc，同样，G21(s)的频率特性可由幅值Kcou和相位θcou表示。

2)令准弹体系下舵指令输入δyc= 0，δzc=sinωt. 同理，可得到

定义 G12(s)= δy/δzc= - G21(s)，G22(s)=δz/δzc=G11(s). 综合以上分析，等效舵机为

式中:G(s)为等效舵机传递函数矩阵，

由G11(s)和G21(s)的频域特性可得到其传递函数

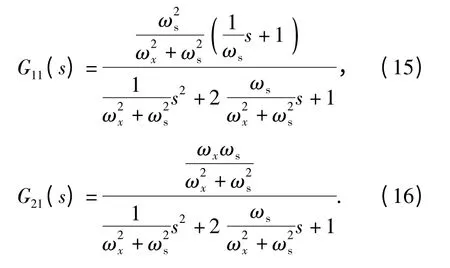
以ωs为无量纲参数，对G11(s)和G21(s)进行无量纲化ω/ωs. 得到无量纲

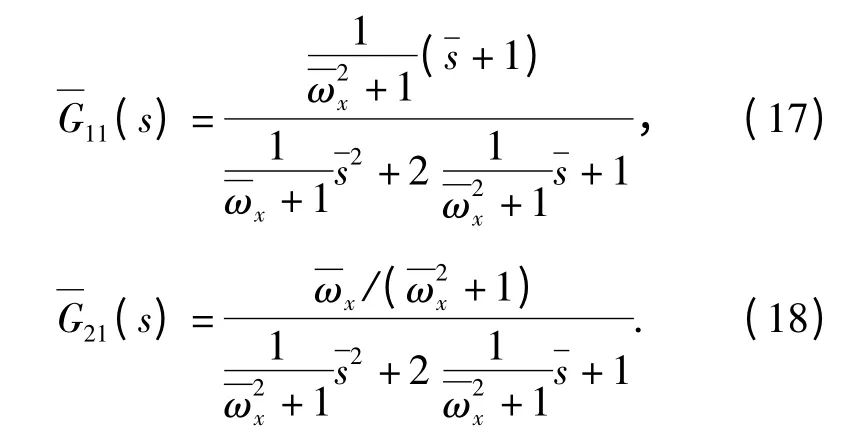
图4 无量纲的G11(s)频域特性Fig.4 Frequency characteristics of dimensionless G11(s)

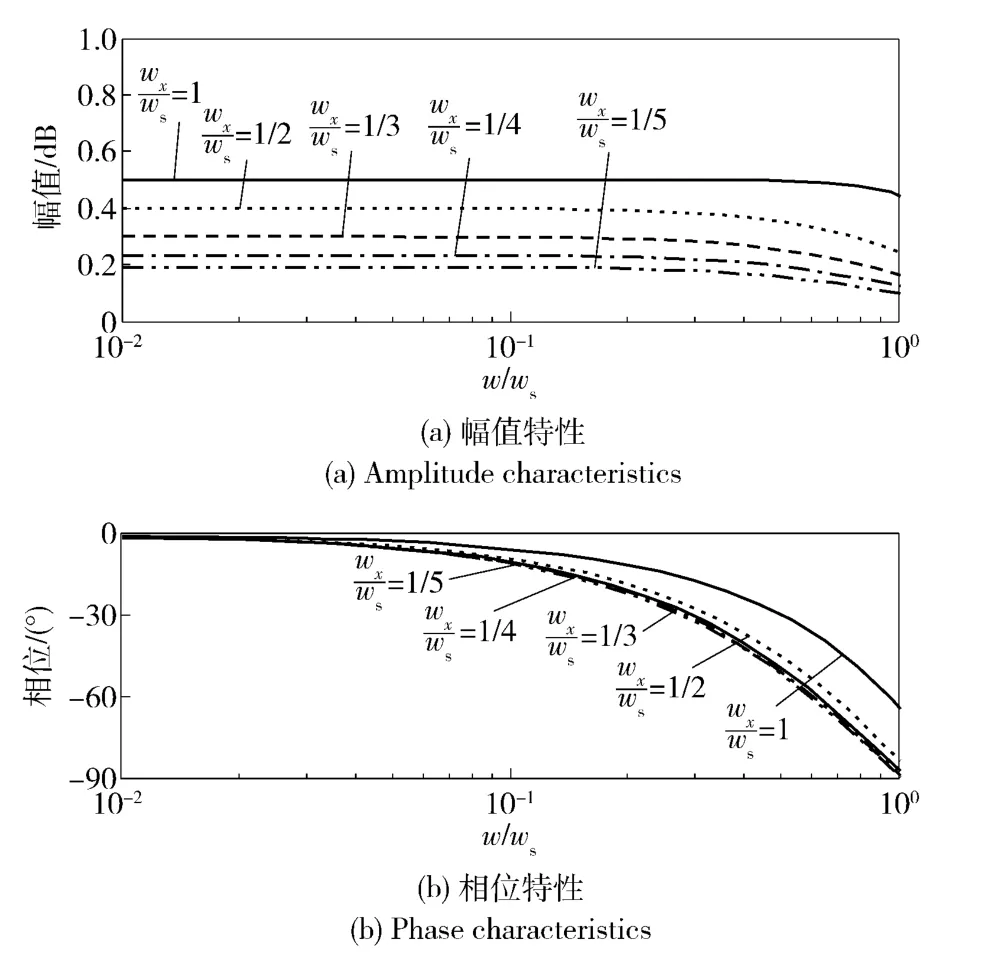
图5 无量纲化的G12(s)频域特性Fig.5 Frequency domain characteristics of dimensionless G12(s)

由于弹体旋转，俯仰和偏航通道间存在控制耦合，等效舵机为双输入双输出线性系统;随着转速与舵机频带比值ωx/ωs的提高，等效舵机传递函数矩阵中主对角元幅值逐渐降低，相位超前;非主对角元幅值逐渐增加，相位超前，两通道间的控制耦合增加。

3 控制耦合解耦方法设计

等效舵机为双输入双输出系统，将等效舵机传递函数矩阵中的非主对角元素消零，即可消除滚转导弹驾驶仪控制耦合。对最优舵面超前角度补偿和输出反馈动态解耦2 种解耦控制方法分别进行了对比研究。

3.1 最优舵面超前角度补偿

从工程实现角度考虑，可将舵面超前一个转角θ，降低控制耦合，如图6 所示。

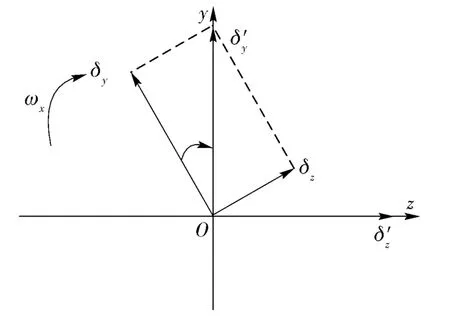
图6 舵机超前角度示意图Fig.6 Schematic diagram of actuator leading angle compensation

超前角度θ 后，等效舵机的输出为

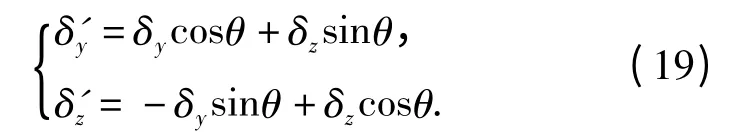
已知在δyc=sinωt、δzc=0 输入下

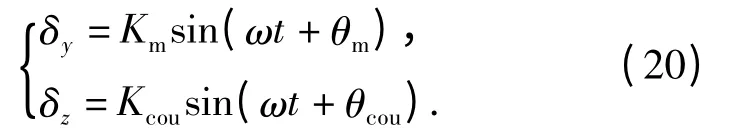
将(20)式代入到(19)式中，得到

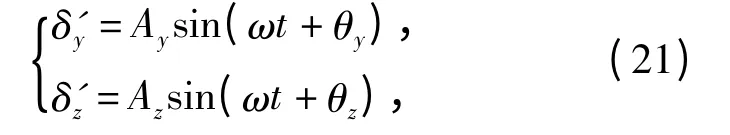
式中:

不同的舵机指令频率ω、转速ωx和舵机频带ωs对应的舵面超前角度θ 如图7 所示。

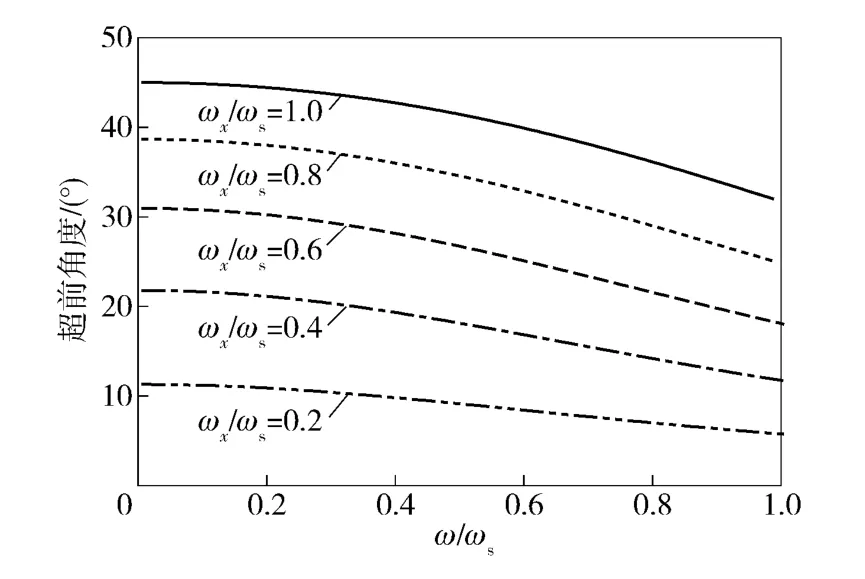
图7 最优舵面超前角度Fig.7 Optimal actuator leading angle

由图7 可知，最优超前角度随着转速与舵机频带比值ωx/ωs的增加而增大，并随舵机指令频率与舵机频带比值ω/ωs的增加而减小。采用最优舵面超前角度补偿的解耦效果如图8 所示。

图8 舵面最优角度超前后解耦效果Fig.8 Decoupling effect of optimal actuator leading angle compensation

采用最优的舵面超前角度补偿，可以降低控制耦合，但不能完全消除，且当转速与舵机频带的比值ωx/ωs、舵机指令频率与舵机频带的比值ω/ωs增加时，主通道输出幅值减小，舵机控制效率降低，耦合通道幅值提高，解耦效果降低。该方法实现简单，利于工程实现。在工程上设计滚转导弹舵机指标时，应保证舵机频带ωs≥2ωx，由图8 可知，此时经最优舵面超前角度补偿后，主通道舵机效率在85%以上，控制耦合在20%以下。

3.2 基于输出反馈的动态解耦设计

输出反馈动态解耦的机理是使受控系统和补偿器间极点—零点准确对消［11］，动态解耦控制系统结构如图9 所示。

图9 动态解耦控制系统结构图Fig.9 Structure diagram of the decoupling control with dynamic output feedback

图9中:G(s)为2 ×2 的等效舵机传递函数矩阵，且G(s)= 不可简约N(s)·D-1(s)，N(s)为G(s)的分子矩阵，D(s)为G(s)的分母矩阵;C(s)为2×2 的补偿器传递函数矩阵，且C(s)=G-1(s)·P(s)=D(s)·N-1(s)·P(s). 其中:

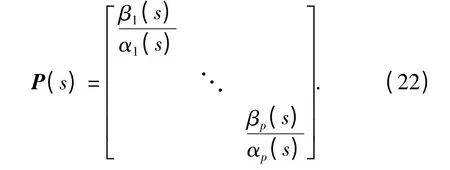
解耦后闭环传递函数矩阵

已知等效舵机传递函数矩阵

给定G(s)的一个不可简约右矩阵分式表述为

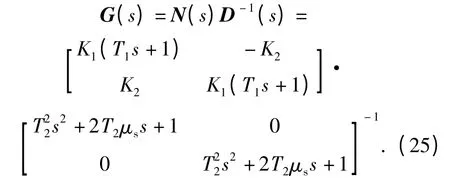
对N(s)和D(s)的极点进行分析可知，N(s)和D(s)稳定。期望的解耦后舵机传递函数与原舵机传递函数相同，则期望的解耦后闭环传递函数矩阵

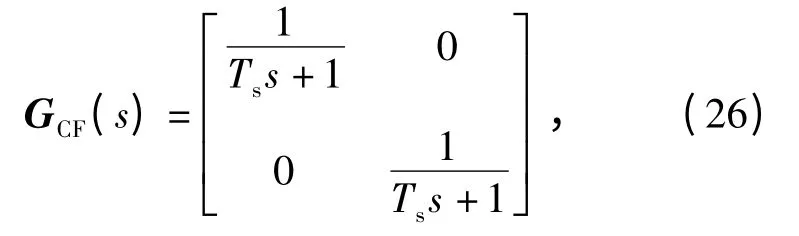
可得出

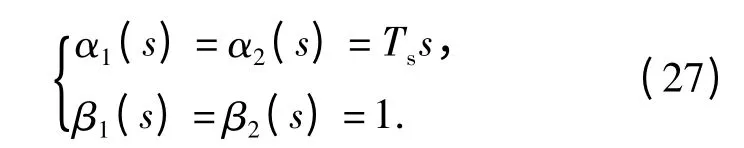
补偿器的传递函数矩阵C(s)可由(28)式表示:

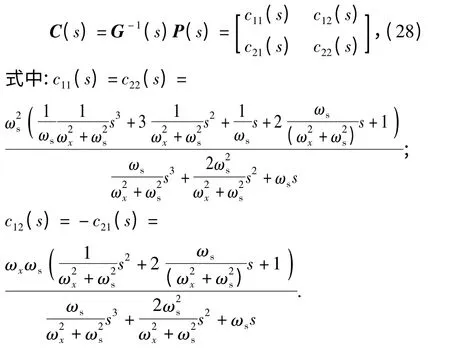
易证，C(s)为真，具备物理可实现性，且仅与舵机频带ωs和转速ωx相关。其中:ωs为舵机已知参数，ωx为弹载转速计测量值。

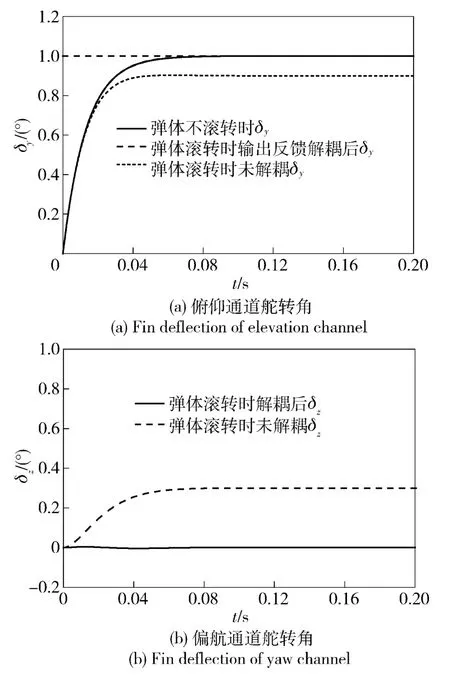
图10 有无输出反馈解耦的舵转角对比Fig.10 Comparison of actuator angles with or without the decoupling control by output feedback

对基于输出反馈的动态解耦方法进行仿真验证。设ωx=4 Hz、ωs=12 Hz，俯仰通道舵转角指令δyc为1°的阶跃指令，偏航通道舵转角指令δzc=0°.俯仰和偏航通道舵转角输出δy和δz如图10 所示。仿真结果证明，输出反馈解耦方法可实现控制耦合的完全消除。

输出反馈解耦补偿器传递函数矩阵C(s)与测量转速ωx相关，当测量转速产生偏差时，输出反馈解耦的效果如图11 所示。可知，测量转速的偏差对输出反馈解耦效果影响很小。

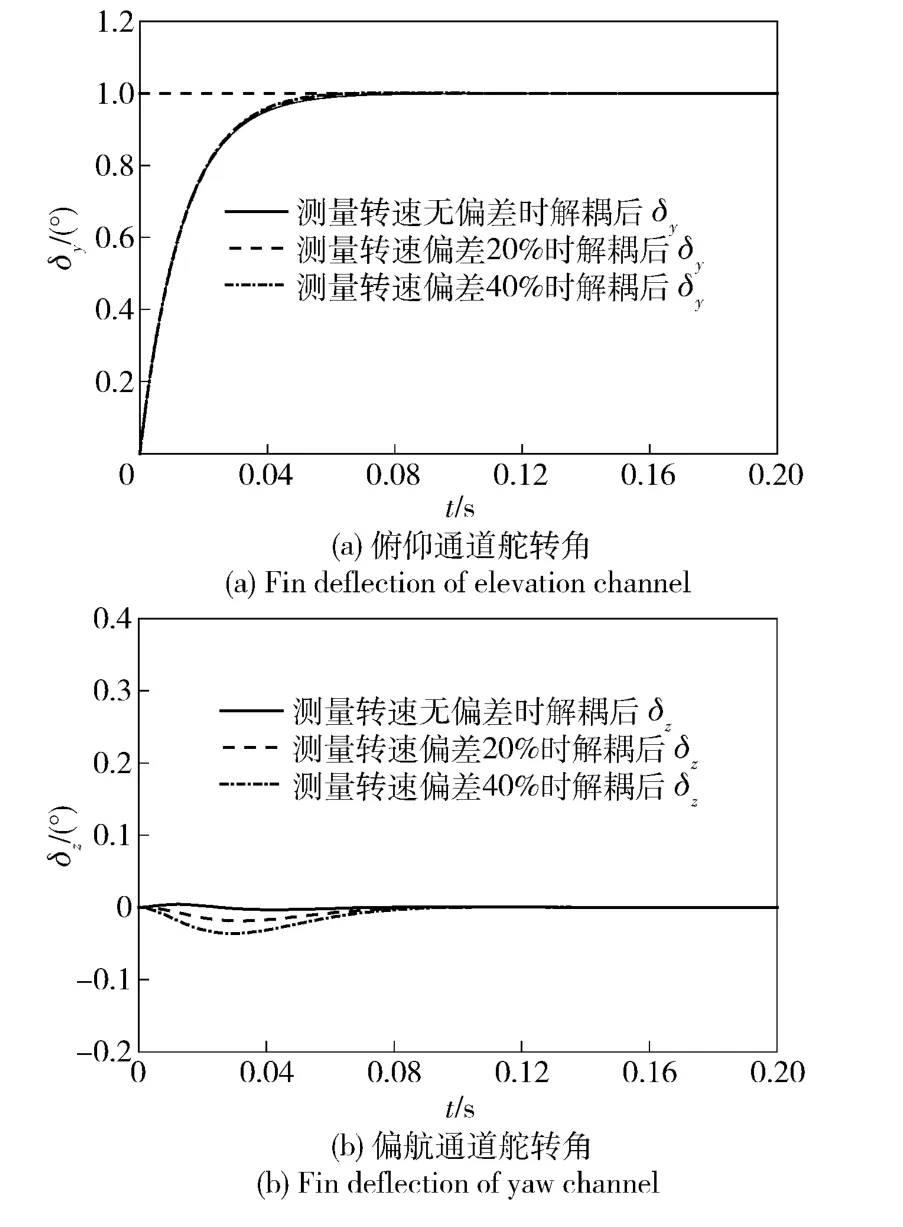
图11 测量转速偏差对输出反馈解耦效果的影响Fig.11 Effect of spinning frequency measurement errors on decoupling control

由于输出反馈动态解耦要求受控系统和补偿器间极点—零点准确对消，因此，要求对舵机传递函数精确已知，且舵机阶数越高，补偿器设计越复杂。

4 结论

通过建立滚转导弹过载驾驶仪模型，分析了俯仰和偏航通道控制耦合的产生机理，推导了等效舵机的传递函数矩阵，分别研究了最优舵面超前角度补偿方法和输出反馈动态解耦方法。研究结果表明:控制耦合的大小与弹体转速和舵机频带的比值相关，最优舵面超前角度补偿方法实现简单，适合工程应用，但当转速和舵机频带的比值、舵机输入频率和舵机频带的比值增加时，解耦效果变差，因此工程上滚转导弹舵机频带设计指标应为转速的2 倍以上;基于输出反馈动态解耦方法能够实现控制耦合的完全解耦，且受测量值的影响较小，但该方法要求对舵机传递函数精确已知，且当舵机阶数增加时，设计的补偿器复杂性相应增加，使该方法在工程应用中受到一定的限制。

References)

［1］Lestage R. Analysis of control and guidance of rolling missiles with a single plane of control fins［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit. Denver:AIAA，2000:14 -17.

［2］Li K，Yang S，Zhao L. Stability of spinning missiles with an acceleration autopilot［J］. Journal of Guidance，Control，and Dynamics，2012，35(3):774 -786.

［3］WANG Zhong-yuan，CHANG Si-jiang. Impact point prediction and analysis of lateral correction of two-dimensional trajectory correction projectiles［J］. Defence Technology，2013，9(1):48-52.

［4］Fleming A W，Lange B O，Parkinson B W. Control synthesis for spinning aerospace vehicles［J］. Journal of Spacecraft and Rockets，1967，4(2):142 -150.

［5］Idan M，Shima T，Golan O M. Integrated sliding mode autopilotguidance for dual - control missiles［J］. Journal of Guidance，Control，and Dynamics，2007，30(4):1081 -1089.

［6］Creagh M A，Mee D J. Attitude guidance for spinning vehicles with independent pitch and yaw control［J］. Journal of Guidance，Control，and Dynamics，2010，33(3):915 -922.

［7］袁天保. 弹道导弹滚动飞行动力学与控制研究［D］. 长沙:国防科学技术大学，2005.YUAN Tian-bao. Research of dynamic and control of spinning ballistic missile［D］. Changsha:National University of Defense Technology，2005. (in Chinese)

［8］Fortescue P W，Belo E M. Control decoupling analysis for gyroscopic effects in rolling missiles［J］. Journal of Guidance，Control，and Dynamics，1989，12(6):798 -805.

［9］陈罗婧，刘莉，于剑桥.双通道控制旋转导弹自动驾驶仪解耦控制研究［J］.北京理工大学学报，2008，28(1):11 -14.CHEN Luo-jing，LIU Li，YU Jian-qiao. Decoupling control of a double channel control rolling missile autopilot［J］. Transactions of Beijing Institute of Technology，2008，28(1):11 - 14. (in Chinese)

［10］Zarchan P. Tactical and strategic missile guidance［M］. Reston:American Institute of Aeronautics and Astronautics，1997.

［11］郑大钟. 线性系统理论［M］. 第2 版. 北京:清华大学出版社，2002.ZHENG Da-zhong. Linear system theory［M］.2nd ed. Beijing:Tsinghua University Press，2002. (in Chinese)