基于EXCEL VBA的灰色数列预测程序实现

王 楠

（西安体育学院，陕西西安，710068）

基于EXCEL VBA的灰色数列预测程序实现

王 楠

（西安体育学院，陕西西安，710068）

本文利用VBA在EXCEL下编写宏程序，实现数列灰色预测，并选取02年至09年《中国体育事业统计年鉴》中我国运动员在奥运会、亚运会、各类世界锦标赛中获得世界冠军的个数作为原始数据列，对2010年至2013年获运动员世界冠军的个数进行验证性预测。

灰色数列预测；VBA；EXCEL

1 灰色系统及灰色数列预测

1.1 灰色系统的基本概念

一个系统的内部特征是完全已知的，即系统的信息是充足完全的，我们称之为白色系统。若一个系统的内部信息是一无所知，只能从它同外部的联系来观测研究，这种系统便是黑色系统。灰色系统介于二者之间，灰色系统的一部分信息是已知的，一部分是未知的。

1.2 灰色数列预测

灰色预测是灰色系统理论的重要组成部分，是一种对含有不确定因素的系统进行预测的方法。它利用连续的灰色微分模型，从而预测事物未来发展趋势的状况。对系统的发展变化进行全面的观察分析，并做出长期预测。灰色预测的基本方法大致可分为数列预测、灾变预测和系统预测，在这些预测方法中，灰色数列预测应用最为普遍，灰色数列预测是指利用GM(1,1)模型，对时间序列进行数量大小的预测。

GM(1,1)预测模型为：

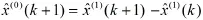
本文选取残差模型对模型进行修正处理，提高预测的准确性和精度。

2 EXCEL VBA的灰色数列预测程序实现

对GM(1,1)预测模型及其残差检验过程，我们可以运用EXCEL2007提供的VB编辑器编写VBA宏程序来实现。

2.1 预测的VBA程序设计

Private Sub hsyc_Click()

Dim x(50), y(50), z(50), q(50), p(50), B(50, 50), c(2, 2), d(2, 2), e(50, 50), f(50, 50)

Dim m(50), h(50), r(50), v(50)

k = Cells(2, 1).Value:n = Cells(3, 1).Value:n = n + k

For i = 0 To k - 1: p(i) = Cells(2 + i, 3).Value: Next i

For i = 0 To k - 1: For j = 0 To i: m(i) = m(i) + p(j): Next j: Next i

For i = 1 To k - 1: B(i, 1) = -1 / 2 * (m(i) + m(i - 1)): B(i, 2) = 1: Next i

For i = 1 To k - 1: c(1, 1) = c(1, 1) + B(i, 1) ^ 2: c(2, 1) = c(2, 1) + B(i, 1): Next i

c(1, 2) = c(2, 1): c(2, 2) = k - 1:t = c(1, 1) * c(2, 2) - c(1, 2) * c(2, 1)

d(1, 1) = c(2, 2) / t: d(2, 2) = c(1, 1) / t: d(1, 2) = -c(1, 2) / t: d(2, 1) = d(1, 2)

For i = 1 To k - 1: B(1, i) = -1 / 2 * (m(i) + m(i- 1)): B(2, i) = 1: Next i

For i = 1 To 2: For j = 1 To k - 1: e(i, j) = d(i, 1) * B(1, j) + d(i, 2) * B(2, j): Next j: Next i

For i = 1 To 2: For j = 1 To k - 1: f(i, 1) = f(i, 1) + e(i, j) * p(j): Next j: Next i :a = f(1, 1): u = f(2, 1)

For i = 0 To n - 1: y(i) = (p(0) - u / a) * Exp(-a * i) + u / a: Next i :x(0) = p(0)

For i = 1 To n - 1: x(i) = y(i) - y(i - 1): Next i

For i = 0 To k - 1: m(i) = 0: c(1, 1) = 0: c(2, 1) = 0: f(i, 1) = 0: Next i

s1 = 0: s2 = 0

For i = 0 To k - 1: s1 = s1 + Abs(x(i) - p(i)): Next i

For i = 0 To n - 1: Cells(2 + i, 4).Value = x(i): Next i

Cells(2 + k, 5).Value = "总残差s1："

Cells(3 + k, 5).Value = s1

For i = 0 To k - 1: Cells(2 + i, 5).Value = x(i) -p(i): Next i

For i = 0 To k - 1: Cells(2 + i, 6).Value = (x(i) -p(i)) / p(i) * 100: Next i

End Sub

2.2 周期修正的VBA核心程序实现

h(1) = (r(0) + r(4)) / 2: h(2) = (r(1) + r(5)) / 2: h(3) = (r(2) + r(6)) / 2: h(4) = (r(3) + r(7)) / 2:

For j = 1 To 4: For i = j - 1 To n - 1 Step 4: v(i) = h(j): Next i: Next j

For i = 0 To k - 1: Cells(2 + i, 7).Value = v(i): Cells(2 + i, 8).Value = v(i) * x(i): Next i

For i = k To n - 1: Cells(2 + i, 7).Value = v(i): Cells(2 + i, 8).Value = v(i) * x(i): Next i

For i = 0 To k - 1: Cells(2 + i, 9).Value = v(i) * x(i) - p(i): s2 = s2 + Abs(v(i) * x(i) - p(i)): Next i

Cells(2 + k, 9).Value = "总残差s2：" :Cells(3 + k, 9).Value = s2

3 用于世界冠军的个数预测的实证分析

选取02年至09年《中国体育事业统计年鉴》中我国运动员在奥运会、亚运会、各类世界锦标赛中获得世界冠军的个数作为原始数据列，对2010年至2013年获运动员世界冠军的个数进行预测。EXCEL数据处理中：n为实测值的个数，m为预测值的个数，图2为和实测值、预测值、修正后数据关联的曲线图。点击“预测”按钮。

此算法根据GM(1,1)预测模型编写，为了提高预测的精度，需要采用残差模型进行周期修正。比较原模型和周期修正后的总残差值S1和S2，可以发现，原模型的总残差51.735大于周期修正残差模型的总残差49.777，说明经过周期修正的模型较原模型预测精度更高。

4 结果分析

通过对图2的实测曲线、预测曲线、周期修正曲线的观察可以看出，利用GM(1,1)模型的预测曲线自2003年之后呈现逐年递增趋势，在大部分年份中，实测曲线在预测曲线附近波动，但也有个别年份例外，如2006年和2008年两年的预测值，就与实测值存在较大的差异和波动，但经过周期修正后的曲线，与真实值较修正前更接近实际值。

徐国祥.统计预测和决策[M].上海：上海财经大学出版社，1998，199-224.

Procedures for the realization of the grey sequence forecast based on Excel VBA

Wang Nan
(Xi’an Physical Education University,Xi’an,710068，China)

The grey sequence forecast is realized by using VBA in Excel macro program.The paper selects the number of champions between 2002 and 2009 in China Sports Statistics Yearbook as the original data to predict and confirm the number of champions between 2010 and 2013.

Grey Sequence Forecast;VBA;EXCEL