运动学涡度及其在湘东雁林寺韧性剪切带中的应用

何国建，金巍，胡为正，卢国安，曾佐勋

（1.江西省地质调查研究院，南昌 330030；2.武汉地质矿产研究所，武汉 430205；3.中国地质大学地球科学学院，武汉430074；4.华中构造力学研究中心，武汉 430074）

运动学涡度及其在湘东雁林寺韧性剪切带中的应用

何国建1，金巍2，胡为正1，卢国安1，曾佐勋3，4

（1.江西省地质调查研究院，南昌 330030；2.武汉地质矿产研究所，武汉 430205；3.中国地质大学地球科学学院，武汉430074；4.华中构造力学研究中心，武汉 430074）

自然界中的剪切带通常是由简单剪切（simple shear）和纯剪切（pure shear）叠加的一般剪切带（general shear）。运动学涡度（kinematic vorticity）的引入提供了一个定量表示两种剪切成分的工具。通过测量剪切带的运动学涡度，可以清楚的了解一般剪切带中究竟是简单剪切还是纯剪切占优势。本文将运动学涡度的基本理论和极摩尔圆法对雁林寺金矿所在的湘东雁林寺韧性剪切带中所表现的运动学涡度进行测量，得出该韧性剪切带的Wk值为0.6，指示其变形以纯剪切为主，且简单剪切作用应变速率比纯剪切作用的应变速率慢。本文从微观运动学层面揭示了湘东雁林寺韧性剪切带对于雁林寺金矿的形成具有重要的意义。

运动学涡度；测量方法；极摩尔圆法；雁林寺韧性剪切带

1 运动学涡度

自然界中的剪切变形包括三种类型：纯剪切、简单剪切和一般剪切（图1）。剪切变形过程中，存在着两非旋转方向或特征向量[2-3]，两特征向量的夹角用υ表示。当υ为90°时，即两非旋转向量或特征向量垂直，为纯剪切，Wk=0；当υ=0°时，即只有一非旋转向量或两非旋转向量平行，则为简单剪切，Wk=1；当0°＜υ＜90°，两非旋向量或特征向量有一锐夹角，就为一般剪切，由不同比例的纯剪切和简单剪切组成[7,12]，Wk值介于0和1之间。自然界中单纯的纯剪切带或简单剪切带很少，大多是由纯剪切和简单剪切组成的一般剪切带。理论上，简单剪切主要导致剪切带的水平移动，含有少量的减薄；一般剪切既引起剪切带的水平移动，也有垂向上减薄；而纯剪切带则经历了大量的减薄，而只含有少量的水平移动[7]。运动学涡度就是用来表示一般剪切带中纯剪切和简单剪切的相对含量。而Bobyarchick[25]将运动学涡度（Wk）定义为Wk=cosυ（1）

式（1）中，υ为两特征方向或非旋转向量间的夹角。根据（1）式，仅有纯剪切变形时，Wk=0；仅有简单剪切变形时，Wk=1。而一般剪切带中既包括纯剪切组分也包含简单剪切组分，因此在一般剪切中，Wk值介于0和1之间。但是，Wk=0.5时，并不意味着纯剪切组分和简单剪切组分相等。运动学涡度处于何值时两种组分相等还存在争议。Tikof f[4]认为当Wk=0.75时才表示纯剪切与简单剪切的作用相等，而Law[13]认为当Wk=0.71时，纯剪切的含量才和简单剪切的含量相等，这种现象称为“纯剪倾向性”[4]。

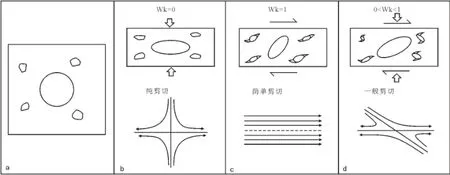
图1 不同剪切带中的岩石变形状态和特征向量特征[7]（据Forte（2007）修改）Fig.1 The feature o f eigenvector and rock de formation in different shears

2 运动学涡度的测量方法

在过去的二十年里，许多方法被用来定量研究天然变形岩石的运动学涡度[14]。碎斑系、重结晶组构、变形的张裂脉、有限应变主轴和剪切带边界的夹角[3-5,15-17,26-27]常用来测量剪切带变形岩石的运动学涡度。这些方法一般是以XZ面（平行于线理，垂直于面理）作为测量平面[14]。大多数的涡度方法只记录了部分的变形历史[13,14,16]，当岩石经历不稳定变形时难以计算出足够精确的运动学涡度值。虽然如此，各种实际应用证明，这些方法在估计平均运动学涡度值和大尺度高应变剪切带的空间变形是有效的[13-14,18-21]。现在最常用的运动学涡度测量方法主要有以下几种：刚性颗粒双曲线分布网法（PHD）[3]、刚性颗粒法（RGN）[17]、石英C轴组构与有限应变[16,22]、石英C轴组构与斜列颗粒形态[22]、极摩尔圆法[3,28-29]等等。

2.1 刚性颗粒双曲线分布网法（PHD）

一般剪切带中包含四类刚性体[2]：1）顺向旋转σ-型变斑或碎斑；2）顺向旋转δ-型变斑或碎斑；3）顺向旋转的σ-δ复合型变斑或碎斑；4）逆向旋转、顺向倾斜的σ-型变斑或碎斑。基于向后旋转的碎斑分布于两特征向量的锐夹角区域内，Simpson and De Paor[3]提出了利用刚性颗粒在双曲线网上的分布（porphyroclast hyperbol ic dist ribution）测量变形岩石运动学涡度的方法。碎斑的长轴和糜棱岩面理之间的夹角为φ（0～90°），以顺时针方向为正向，正的φ值表示向前旋转的碎斑，负的φ值表示向后旋转的碎斑[7]。将样品中碎斑轴率（碎斑长短轴之比）和φ值投影在De Paor双曲线赤平投影网[30]上（图2）。包含所有向后旋转碎斑的双曲线的两翼的夹角即为两特征向量之间的锐夹角。则根据（1）式即可求得变形岩石的运动学涡度。

For te[7]在该法的基础上提出了改进的PHD法。在变形带中采集标本，垂直于糜棱岩面理，平行于线理切制变形岩石薄片。测量薄片中碎斑的φ值。为了减少误差，该方法至少要测量40个碎斑。D碎斑的最小φ值决定了变形岩石的运动学涡度，可通过下式计算：

φmin为碎斑长轴方向和糜棱岩面理之间的夹角最小值。这样，就可以将碎斑方向和轴率投在De Paor的双曲线网上直观的表现出来（图3）。Passchier[18]提出该方法应剔除轴率小于1.4的碎斑，近圆形的碎斑实际上不是向后旋转的。实践中难以准确区分向前旋转和向后旋转的碎斑，这种方法获得的运动学涡度误差较大[2]。

2.2 刚性颗粒法（RGN）

Passchier[15],Simpson and De Paor[3]和wal ls[19]利用刚性碎斑求取高应变带中变形岩石的运动学涡度都建立在Wm（平均运动学涡度）和B*（形

态因子）的关系上。形态因子定义为：

时光荏苒，日月如梭，那个素履追梦的青葱少年转眼间已生华发，但当老师的他了有新的梦想——做不凡的造梦者。他的教育目标是培养德才兼备的创新人才。他认为当一位学生有了健全的人格、创新思维和自我意识之后，高考就只是一件附加品。

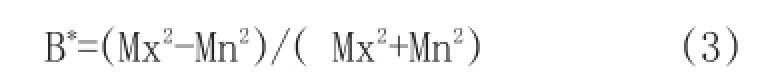
Mx表示碎斑的长轴，Mn表示碎斑的短轴。而在一般剪切带中，塑性基质中的刚性旋转碎斑记录了一个临界形态因子。小于临界形态因子，刚性碎斑不断向前旋转；大于临界形态因子，刚性碎斑处于一种稳定状态[17,23,31]。则运动学涡度可以下式求取：

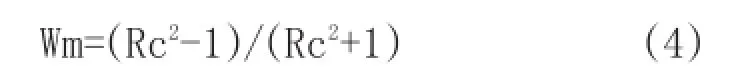
Rc为刚性碎斑的长短轴之比。Passchier[15]在Wm、B*和θ之间的关系：

θ为碎斑的长轴与糜棱岩面理之间的夹角。根据（5）式关系，Jessup et al[17]建立了刚性碎斑网（RNG，图3）。将测量计算的θ和B*投在RGN上，便可求出变形岩石的运动学涡度。

2.3 石英C-轴组构和有限应变法

一般情况下，我们实际测量的数据是变形后的最终结果，无法确定变形过程中的某一瞬时应变值。为了解决这一问题，常假定变形过程中,瞬时剪应变相对瞬时伸长度的大小保持恒定，便可用实际可测的有限应变取代瞬时应变。这样所测定的运动学涡度为某一变形事件的平均运动学涡度（Wm）[7]。单斜变形中，有限应变椭球的长轴向非共轴变形的剪切平面或者共轴变形的流面旋转[21]。该旋转轴为不稳定的涡旋向量[16,18,29]。这样，结合有限应变和石英C-轴组构中心环带法线和糜棱岩面理之间的额夹角便可求出变形岩石Wm，其关系[5,16]如下：

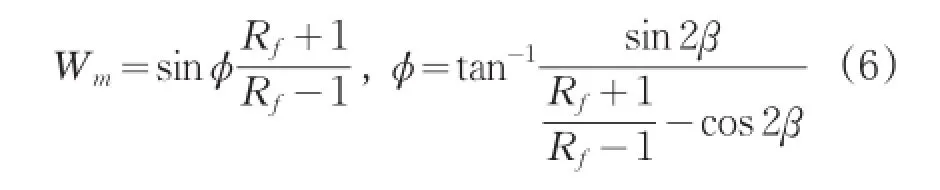
其中Rf为岩石XZ面的有限应变值，β为石英C轴组构中心环带的法线和糜棱岩面理之间的夹角。根据wal ls[16,18］，石英C-轴组构中心环带法线和糜棱岩面理之间的夹角等于剪切面方向和有限应变主面的夹角，加上通过有限应变测量测出的XZ面的Rf[1]，即可求出平均运动学涡度。

图2 PHD图解法[30]Fig.2 Diagram o f PHD

2.4 石英C-轴组构与斜列颗粒法

Passchier[15]提出了利用石英C-轴组构和斜列颗粒形态之间的关系计算运动学涡度的方法。在二维应变中，θ是ISA与剪切面间的锐夹角。则可由Wk=sin2θ计算变形岩石的运动学涡度。剪切面的方位可由石英C-轴组构确定。在变形岩石的最后增量变形中，新生晶粒在平行于瞬时应变伸长轴（ISA）的方向被拉长，而早期晶粒将向有限应变压扁面方向旋转，并因发生重结晶作用和颗粒边界移而改变[21]。因此，与面理成最大交角的新生斜列颗粒的长轴方位即为ISA的大致方位。通过新生斜列颗粒长轴方位的测量，即可求取变形岩石的运动学涡度。岩石的增量变形记录了岩石最后一期变形特征，则该方法只能用于测量经历稳定变形历史的岩石或者经历多次变形岩石的最后一期的变形特征[21]。

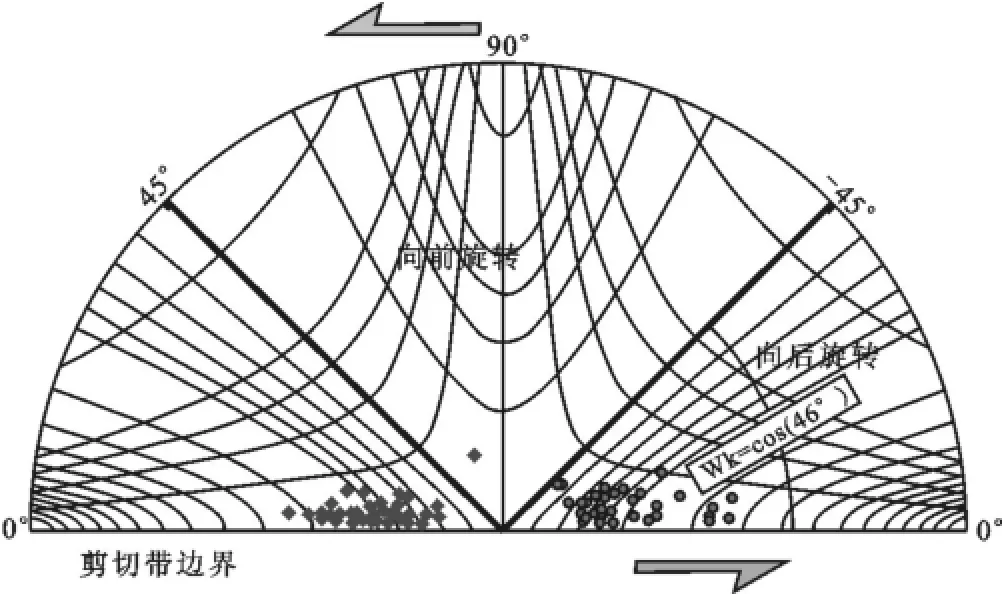
图3 刚性颗粒的轴率和长轴方向的极射赤平投影（据Forte[7]修改）Fig.3 Hyperbo lic stereonet p lot o f axia l ratios and long axis orientations o f rotated porphyroc lasts

2.5 极摩尔圆法

极摩尔圆通过求取变形面内两特征向量方向的夹角υ来计算运动学涡度。Simpson[3]最先提出了建立极摩尔圆的方法。张进江等[28，29]在此方法基础上进行改进。利用应变椭圆轴比Rs及最大应力轴方向与剪切面夹角α建立极摩尔圆（图4）。具体方法[28-29]为：①设O为坐标原点，做直线O-1-Rs（其中O-1为单位长度，O-Rs为应变椭球轴比），并以1-Rs为直径做圆，就得到了剪切带的极摩尔圆；②自Rs点作直线Rs-O′，使之与直线O-1-Rs的夹角为α，直线Rs-O′与极摩尔圆的交点就是第二特征向量（ζ2, 0）；③由坐标原点过点（ζ2,0）的直线则是参考轴，它与实际空间中的剪切面垂直，参考轴与极摩尔圆的另一个交点为另一个特征向量（ζ1,0）；④从点（ζ2,0）向摩尔圆一侧做参考轴的垂线，其与摩尔圆的交点为锚点（So,ψo），锚点与两个特征向量（ξ1,0）和（ξ2,0）连线之间的夹角极为两特征向量之间的夹角υ；⑤从圆上量出特征向量的夹角υ，由Wk=cosυ求得运动学涡度。

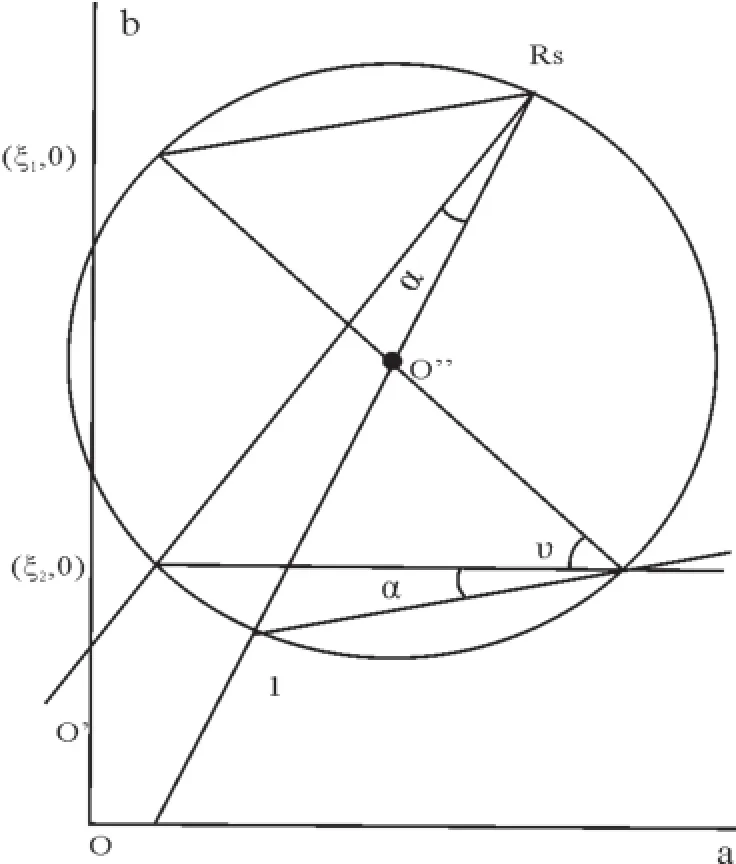
图4 一般剪切的极摩尔圆[28]Fig.4 Po lar Mohr circ le o f genera l shear

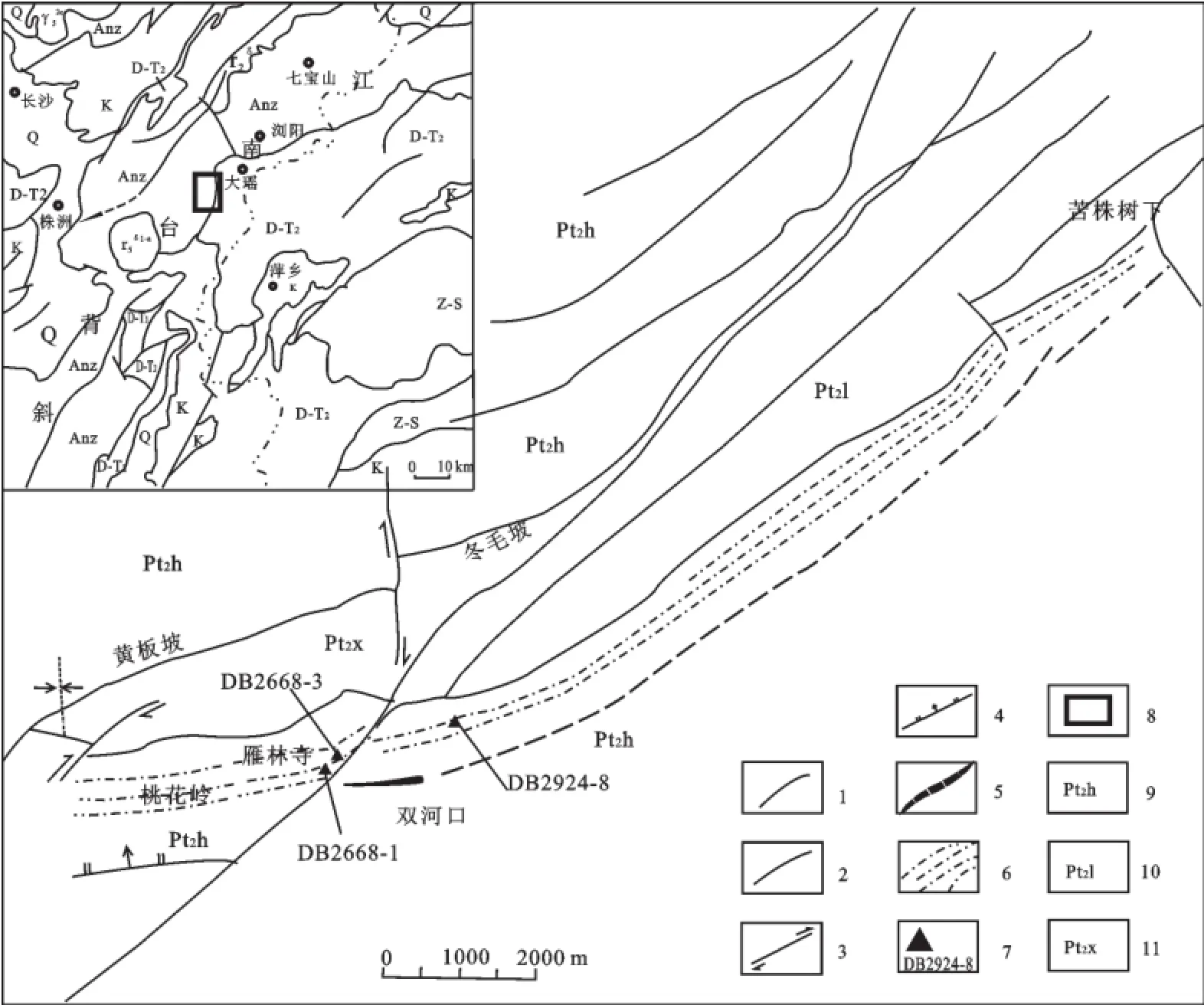
图5 湘东雁林寺韧性剪切带构造简图Fig.5 Tec tonic ske tch m ap o f the Yan linsi duc tile shea r zone in easte rn Hunan Province

3 雁林寺韧性剪切带的运动学涡度

湘东雁林寺金矿是近年继半边山金矿发现以来的又一大型金矿在该地区被发现。黄诚[32]等认为雁林寺金矿围岩冷家溪群中早期的劈理化带和改造早期劈理化带的韧性剪切带共同组成矿区的储矿构造体。剪切带形成的糜棱岩化和劈理化带为金元素的富集成矿提供了部分物质基础，并为成矿元素迁移提供了运输通道。通过对含金石英脉进行ERS测年得出韧性剪切带形成时间是177.4～155.0 Ma，为燕山早期[33]。

湘东雁林寺韧性剪切带位于扬子地台江南台背斜的东南缘，与华南褶皱系紧邻。西起牛家田，呈近东西向延伸至肖家冲、雁林寺北附近被北东向断层站头－上官山断层破坏错移，然后转为北东向经报信岭，苦株树下延至棉花冲北东附近被西源冲-桃园冲断层断失，区内延长达14 km，剪切带最宽处可达1000 m左右（图5）。

剪切带内岩石变形明显，主要为强烈的面理化带，但在不同区段岩石变形程度存在差异。在东段的苦株树下一带，剪切带呈北东－南西向展布，带宽达400 m以上，带内岩石主要表现为强烈的面理化，岩石中的鲕状赤铁矿变形后明显压扁拉长，石英具有一定程度的拉长。在XY面上可见明显的拉伸线理，其产状235°∠20°，所见的压扁赤铁矿旋转现象不明显。在高峰大队可见明显的黄铁矿压力影、石英颗粒旋转碎斑和雁列脉（图6a），表明该剪切带为右行，与室内显微观察的结果相一致（图6b）。

图6 a右行的雁列脉；b糜棱岩化浅变质杂砂岩中的旋转碎斑Fig.6 a.En eche lon right betera l veins;b.Rotating porphyroc last o fm ylonitization g reyw acke w ith ep izona lm e tam o rphism

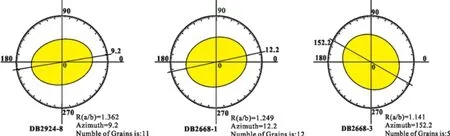
图7 样品DB2924-8、DB2668-1和DB2668-3的应变椭圆Fig.7 Strain e llipse o f DB2924-8,DB2668-1 and DB2668-3 sam p les

剪切带处于冷家溪群黄浒洞组中，主要发育一套糜棱岩化的浅变质碎屑岩，石英的含量比较高。综合各方面的考虑，使用极摩尔圆法测定该韧性剪切带的运动学涡度最为合适。选取剪切带内典型的三块样品，测量其有限应变值。采用中国地质大学（武汉）构造模拟实验室李志勇等提出的利用惯量椭球对任意形状矿物颗粒进行描述的方法[33]对雁林寺韧性剪切带之中三个定向样薄片进行应变椭球分析，在高倍显微镜下对薄片中的XZ面上的石英集合体进行轴率Rs的测量，取得三组有效Rs值（图7）。最大应力轴方向与剪切面的夹角θ可在室内通过高倍显微测量或地质罗盘测量韧性剪切带露头上S剪

切面理和C剪切面理的夹角获取。而本文中的θ角是在雁林寺韧性剪切带露头上通过地质罗盘直接测量所得,每个样品采集点测量一组S剪切面理和C剪切面理的夹角，再对各组θ角测量结果求算术平均,得到θ角的有效平均值（表1）。根据上述提出的极摩尔圆运动学涡度测量方法，采用雁林寺韧性剪切带中的Rs和θ值编制极摩尔圆，并取得三组非旋转向量夹角υ值，取υ余弦值取得三个雁林寺韧性剪切带运动学涡度值：Wk1=0.5、Wk2=0.63、Wk3=0.54（图8）。此外对雁林寺韧性剪切带的运动学极摩尔圆分析并计算得出剪切带剪切变形过程中纯剪切应变速率和简单剪切应变速率之比ε/γ（表1）。

表1 湘东雁林寺韧性剪切带运动学涡度值Table 1 Kinematic vorticity va lue numb le o f the Yan linsiductile shear zone in eastern Hunan Province

4 结论与讨论

自然界剪切带多数为一般剪切带，对其纯剪切组分和简单剪切组分的比率进行定量分析，是确定剪切作用类型的基础。运动学涡度分析有助于获得变形区域的运动学特征，为描述剪切作用类型提供定量尺度。到目前为止，测量运动学涡度的方法有很多种，本文选择了极摩尔圆法测量雁林寺韧性剪切带的运动学涡度。极摩尔圆法以石英颗粒的形态比为基础，通过测量变形石英颗粒的有限应变，然后编制极摩尔圆来求取剪切带的运动学涡度。从表1中可以看出，雁林寺韧性剪切带中的三处样品测得的S剪切面理和C剪切面理的夹角有一定的差别，但测得的运动学涡度基本上一致，都在0.6左右。这表明，雁林寺韧性剪切带是具有简单剪切和纯剪切的一般剪切带。

在雁林寺韧性剪切带剪切变形的事件中，纯剪切占据着主导地位，即雁林寺韧性剪切带的变形除了以纯剪切为主外，还存在一个简单剪切分量，说明形成剪切带的驱动力不是平行于剪切带边界的，而是与剪切带边界有一定的交角。剪切作用以挤压为主，但也有部分走滑的成分，根据纯剪倾向性[4]，在Wk=0.71时，才表示纯剪切与简单剪切的作用相等。这也说明了使雁林寺韧性剪切带活动的主应力并不

是平行于剪切带走向的，也不是垂直于剪切带走向的，而是与剪切带的走向有一定的夹角。通过剪切带的运动学涡度和极摩尔圆还可以计算得出雁林寺韧性剪切带形成过程中纯剪切应变速率和简单剪切应变速率之比[29]。表1所示，在雁林寺韧性剪切带中，纯剪切与简单剪切的应变速率之比都小于1，说明变形过程中，简单剪切作用应变速率比纯剪切作用的应变速率快。

力的作用方向影响着物质迁移的方向，雁林寺韧性剪切带的形成为雁林寺金矿的形成提供了的物质运输通道和巨大储矿空间，雁林寺韧性剪切带有较好的金矿找矿前景。

[1]郑亚东,常志忠.岩石有限应变测量及韧性剪切带[M].北京:地质出版社,1985.

[2]郑亚东,王涛,张进江.运动学涡度的理论与实践[J].地学前缘,2008,15(3):209-220.

[3]Simpson C,DePaor D G.Strain and kinematic analysis in general shear zones[J].Journal of Structural Geology, 1993,15:1－20.

[4]Tikoff B,Fossen H.Limitations of three dimensional kinematic vorticity analyses[J].Journal of Structural Geology,1995,17:1771－1784.

[5]Passchier CW,Urai JL.Vorticity and strain analysis using Mohr diagrams[J].Journal of Structural Geology, 1988,10(8):755－763.

[6]P X Ypolias，l K Koukouvelas.Kinematic vorticity and strain rate patterns associated with ductile extrusion in the Chelmos Shear Zone(External Hellenides,Greece)[J]. Tectonophysics,2001,338:59－77.

[7]Forte A M,Christopher M.Bailey.Testing the utility of the porphyroclast hyperbolic distributionmethod of kinematic vorticity analysis[J].Journal of Structural Geology, 2007,29:983－1001.

[8]Scott E.Johnson,Hendrik J.Lenferink,Nancy A.Price,et al.Clast-based kinematic vorticity gauges:The effects of slip at matrix/clast interfaces[J].Journal of Structural Geology,2009,31,1322－1339.

[9]Truesdell,C.Twomeasures of vorticity[J].Journal of Rational Mechanics and Analysis,1953,2,173－217.

[10]McKenzie,D.Finite deformation during fluid flow[J]. Geophysical Journal of the Royal Astronomical Society, 1979,58,689－715.

[11]Means W D,Hobbs B E,Lister G S,et al.Vorticity and non-coaxiality in progressive deformations[J].Journal of Structural Geology,1980,2:371－378.

[12]Jackie Langille,Jeffrey Lee,Brad ley Hacker,et al.Middle crustal ductile deformation patterns in southern Tibet:Insights from vorticity studies in Mabja Dome[J]. Journal of Structural Geology,2010,32:78－85.

[13]Law R D,Searle M P,Simpson R L.Strain,deformation tem peratures and vorticity of flow at the top of the Greater Himalayan Slab,Everest Massif,Tibet[J].Journal of the Geological Society of London,2004,161:305－320.

[14]P.Xypolias.Some new aspects of kinematic vorticity analysis in naturally deformed quartzites[J].Journal of Structural Geology,2009,31:3－10.

[15]Passchier C W.Stable positions of rigid objects in non-coaxial f ow:a study in vorticity analysis[J].Journal of Structural Geology,1987,9:679－690.

[16]Wallis S R.Vorticity analysis in a metachert from the Sanbagawa belt,SW Japan[J].Journal of Structural Geology,1992,14:271－280.

[17]Jessup M J,Law R D,Frassi C.The rigid grain net(RGN):an alternative method for estimating mean kinematic vorticity number(Wm)[J].Journal of Structural Geology2007,29:411-421.

[18]Wallis SR.Vorticity analysis and recognition of ductile extension in the Sanbagawa belt,SW Japan[J].Journal of Structural Geology,1995,17:1077－1093.

[19]Grasemann B,Fritz H,Vannay JC.Quantitative kinematic f ow analysis from the Main Central Thrust Zone (NW-Himalaya,India):implications for a decelerating strain path and the extrusion of orogenic wedges[J]. Journal of Structural Geology,1999,21:837－853.

[20]Bailey C M,Eyster E L.General shear deformation in the Pinaleno Mountainsmetamorphic core complex,Arizona[J].Journal of Structural Geology,2003,25:1883－1893.

[21]Sullivan W A.Significance of transport-parallel strain variations in part of the Raft River shear zone,Raft River Mountains,Utah,USA[J].Journal of Structural Geology,2008,30:138－158.

[22]Wallis S R.Vorticity analysis and recognition of ductile extension in the Sanbagawa belt,SW Japan[J]. Journal of Structural Geology,1995,17:1077－1093.

[23]Sarkarinejad K,Godin L,Faghih A.Kinematic vorticity f ow analysis and40Ar/39Ar geochronology related to inclined extrusion of the HP-LT metamorphic rocks along the Zagros accretionary prism,Iran[J].Journal of Structural Geology,2009,31:691－706.

[24]Fossen H,Tikoff B.The deformationmatrix for simultaneous simple shearing,pure shearing and volume change,and its app lication to trans-pression-transtension tectonics[J].Journal of Structural Geology,1993,14: 413－422.

[25]Bobyarchick,A.The eigenvalues of steady state flow in Mohr space[J].Tectonophysics,1986,122:35－51.

[26]Law R D.Knipe R J.Dayan H.Strain-path partitioning within thrust sheets:microstructural and petrofabric evidence from the Moine thrust zone at Loch Eriboll, northwest Scotland[J].Journal of Structural Geology, 1984,6:477－497.

[27]Platt J P.Behrmann J H.Structures and fabrics in a crustal scale shear zone,Betic Cordilleras,S.E.Spain [J].Journal of Structural Geology,1986,8:15－34.

[28]张进江,郑亚东.运动学涡度、极摩尔圆及其在一般剪切带定量分析中的应用[J].地质力学学报,1995,14(3):55－64.

[29]张进江,郑亚东.运动学涡度和极摩尔圆的基本原理与应用[J].地质科技情报,1997,16(3):33-39.

[30]De Paor D G.Rf/φf st rain analysis using an orientation net[J].Journal of Structural Geology,1988,10:323－333.

[31]Ghosh SK,Ramberg H.Reorientation of inclusions by combination of pure and simple shear[J].Tectonophysics,1976,34:1－70.

[32]黄诚,樊光明,姜高磊,等.湘东北雁林寺金矿地质地球化学特征及矿床成因[J].大地构造与成矿学，2012,36（1）: 76-84.

[33]李志勇,曾佐勋.利用惯量椭圆进行岩石有限应变分析[J].地质科技情报,2006,25（6）:37－40.

K inematic Vorticity and its App lication to the YanlinsiDuctile Shear Zone in Eastern Hunan Province

HEGuo-jian1,JINWei2,HUWei-zheng1,LUGuo-an1,ZENG Zuo-xun3,4

(1.Geological Survey of JiangxiProvince,Nanchang,330030,China;2.Wuhan Institude of Geology and M inerals Resources,Wuhan, 430205,China;3.Faculty of Earth Sciences,China University of Geosciences,430074,China;4.Huazhong Tectonomechanical Research Centre,Wuhan,430074,China)

In nature,shear can be decomposed into pure shear componentand simple shear component.Kinematic vorticity can quantitatively evaluate the componentof simple shear and pure shear.Bymeasuring the kinematic vorticity number(Wk),we can clearly understand that in the general shear zone,the simple shearor pure-shear is dom inant shear force.This paper introduces basic theory and severalmeasuring methods of kinematic vorticity number,andmeasresWk of Yanlinsiductile shearzoneby polarMohr constructions.Itshows that theWk isnearly 0.6,which indicates that the shear zone is exactly existand dom inated by pure shear,and straining rate of simple shear is slower than pure shear.It reveals the important significance of the Yanlinsiductile shear zone for the Yanlinsigold deposit formation,inm icrokinematics.

kinematic vorticity;method ofmeasurement;polarMohr circle;Yanlinsiductile shearzone

P542+.3

A

1672－4135（2014）02－0136-08

2014-01-04

湖南省国土资源厅“湖南大瑶-王仙地区矿产远景调查项目”（20086205）

何国建（1987-），男，学士，助理工程师，现任职于江西省地质调查研究院，主要从事区域地质矿产调查中构造和矿产方面的工作，E-mail：hunter927@163.com。