煤层气数值模拟的二维交替隐式求解
陈 林 潘 毅 苏 静 王富平 李宜南 冯庆华
(1.成都理工大学能源学院,四川 成都 610059;2.中国石油西南油气田公司川中油气矿,四川 遂宁 629000;3.油气藏地质及开发工程国家重点实验室·西南石油大学,四川 成都 610500;4.中国石油西南油气田公司天然气经济研究所,四川 成都 610051)
煤层气数值模拟的二维交替隐式求解
陈 林1,2潘 毅3苏 静2王富平4李宜南2冯庆华2
(1.成都理工大学能源学院,四川 成都 610059;2.中国石油西南油气田公司川中油气矿,四川 遂宁 629000;3.油气藏地质及开发工程国家重点实验室·西南石油大学,四川 成都 610500;4.中国石油西南油气田公司天然气经济研究所,四川 成都 610051)
数值模拟是确定煤层气开发方案和评价采收率的有效方法,目前广泛应用的三维全隐式差分法求解难度大,计算复杂。根据煤层气的储气特征、吸附特征和解吸机理建立了反映煤层气解吸、扩散及渗流过程的气、水两相耦合流动三维数学模型,模型考虑了煤层非均质各向异性的影响,运用块中心差分格式,对气、水相偏微分方程进行空间差分和时间差分,采用二维交替隐式求解,实现了煤层气数值模拟计算。在此基础上开发出煤层气井数值模拟软件,适用于煤层气整个开采期,可以对煤层气生产进行预测,以此制定合理的开发方案,优化煤层气开采。
煤层气 非均质各向异性 二维交替隐式解法 数值模拟 生产预测
0 引言
煤层气气水两相渗流耦合模型是一复杂高阶非线性数学模型,涉及到的参数较多,包括流体饱和度、相对渗透率、煤层气的平衡吸附量等,再加上一些辅助方程,模型的求解难度较大。笔者建立了反映煤层气解吸、扩散及渗流过程的气、水两相耦合流动三维数学模型,并采用块中心差分格式,相对于煤层的平面展布厚度较薄,简化为平面二维模型,通过采用二维交替隐式法求解,实现了数值模拟计算[1]。
1 数学模型的建立
1.1 基本假设
煤层被认为由基质微孔系统和裂隙宏观孔隙系统组成的双孔单渗特殊双重介质;储层具有非均质、各向异性;煤层内的流动为等温流动,原始状态下被水100%饱和,不含游离气及溶解气,气体均以吸附态储集在煤基质的内表面;气体在裂隙系统中的流动服从渗流和扩散机理,水的流动机理为渗流,渗流和扩散分别服从Darcy定律及Fick第一定律;井筒水平段流动过程中无压损。
1.2 基质系统中解吸扩散方程
煤层气解吸用Langmuir等温吸附方程描述[2]:

式中,Ve为基质—裂隙面上煤层气的平衡吸附量,m3/t;pfg为裂缝系统中气相的压力,MPa;VL为Langmuir体积,即单位体积固体的最大吸附量,m3/t;b为Langmuir常数,1/MPa。
煤层气从基质向割理的扩散遵循Fick第一定律,认为解吸速度与煤基质内表面气体浓度和煤基质中平均浓度的差成正比,定义吸附时间常数

式中,τ为吸附时间常数;Vm为基质中吸附气平均含量,m3/kg;Dm为煤基质的气体扩散系数,m2/d;σ为Warren-Root形状因子,与基质单元的尺寸大小和形状有关;Bg为气体的体积系数;qvm为单位体积储层的煤基质表面煤层气经解吸扩散进入裂隙系统中
的速率,m3/(m3·d);ρc为煤层基质密度,kg/m3。
1.3 裂隙系统气、水流动方程
对于裂隙系统,气体从基质块中不断扩散进入其中,可以看作连续性方程中的源项,裂隙系统中气相的流动方程为[3]:

式中,Krg为气相相对渗透率;μg为气体的黏度,mPa·s;γg为气体的重度,γg=ρgg,N/m3;Df为裂隙的气体扩散系数,m3/d;qvg为井点所在网格单位体积储层的产气量,m3/(m3·d);φf为裂隙的孔隙度,小数;Sg为裂隙中气体的饱和度,小数;Kf为裂缝系统绝对渗透率,mD;H为基准高度,m。
裂隙系统中的水相主要以渗透方式运移,利用连续性方程和Darcy定律,可得水相的流动方程为:

式中,Krw为水相相对渗透率;Bw为水的体积系数;μw为水的黏度,mPa·s;ρw为水的密度,kg/m3;Pfw为裂隙系统中水相压力,MPa;Sw为含水饱和度。
1.4 气、水产量方程
采用三维直角坐标块中心网格,煤层厚度方向为Z方向,并取向下为正,定向羽状水平井位于XY平面上,垂向坐标为Z=0。X,Y,Z方向上网格编号分别用i,j,k表示,编号的顺序X是由左到右,Y是由里到外,Z是由上到下,并规定重力方向向下(图1)。

图1 煤层气水平井网格剖面图
XY平面上的网格将煤层气水平井分为若干微段,由于每段长度较短,可认为煤层气藏流入该段内的流量均匀分布,则对任意网格,给定井筒流动压力,单位体积煤层的产量qvw,qvg计算方法如下[4]:
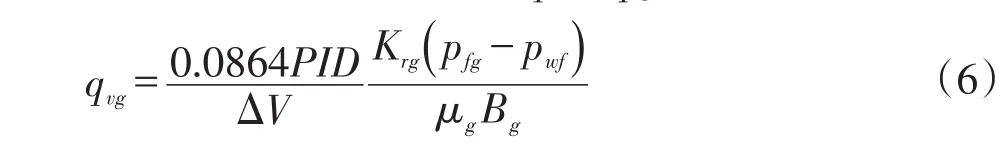

式中,pwf为该网格内所包含井段的井筒流压,MPa;PID为井指数[1]P48,在没有井段的网格,PID=0

式中,Ke为煤层各向异性介质等价的同等渗透率,,kx、ky、kz分别为x,y,z方向的渗透率,mD;Lp为变换的空间上网格内井段的长度,m,L为位于该网格内井段的长度,m;ω为与x轴的夹角,°;rb是井格块的等效半径,m;,
rw为等效井径,m;rwx=Rwxcosω,rwy=RwysinωR为w真实井径,m;S为表皮因子,小数。
1.5 定解条件
初始条件:给定煤层气开发的某一时刻作为初始时刻,给定此时刻的煤储层内的压力分布和饱和度分布为:

式中,pi为裂隙系统初始压力,MPa;Swi为裂隙系统初始含水饱和度,小数;Vmi为初始含气量,m3/t。
外边界条件:在煤层气储层数值模拟中,一般取定压边界或封闭边界,即:pfg|Γpi
内边界条件:在煤层气储层数值模拟中,给定井底流动压力。
1.6 煤层气开采数学模型
相对于煤层的横向展布,煤层厚度相对较薄,可只考虑平面上流动,简化为二维渗流模型,根据物质平衡原理,描述煤储层中煤层气解吸扩散、运移及产出的完整数学模型如下:

2 模型的数值求解
采用块中心差分格式,对气、水相偏微分方程的左端项进行空间差分,右端项进行时间差分。结合渗透率方程、扩散方程、黏度方程、体积系数方程等,采用交替隐式解法求解。如果按全隐式差分直接从时间步n求出下一时间步n+1时的压力和流体饱和度分布,则需要求解一个xy维的方程组。通过利用交替隐式解法,在时间步n到n+1间加入过渡时间步n+0.5,从n到n+0.5只在x方向上求解,从n+0.5到n+1只在y方向上求解,这样就把方程的维数大大降低了,增加了求解的速度,此方法是无条件收敛的[5-6]。
即n到n+0.5时间步,采用如下差分形式:

n+0.5到n+1时间步,采用如下差分形式:

3 算例分析
用以上模型及解法编制了煤层气多分支水平井数值模拟程序,模拟了沁水盆地某区块定向羽状水平井开采过程,单组羽状水平井井身结构如图2所示,水平井地面距离直井100m,水平井主支穿过煤层段约1200m,水平井段左右各打6个分支井眼,分支长93~800m,间距200m,一个井组控制面积约4.9km。该区块煤层参数见表1。

图2 羽状水平井结构图
图3和图4分别是该井组8年产量和累积产量预测结果,产气量峰值是7.7×104m3/d,出现峰值的时间在排水开采320d后[7]。与同等条件煤层气产量模拟曲线[1]P50相比,两者高峰期以及日产量和累积产量总趋势相近。

表1 煤层数值模拟基础参数表

图3 煤层气产量模拟结果图
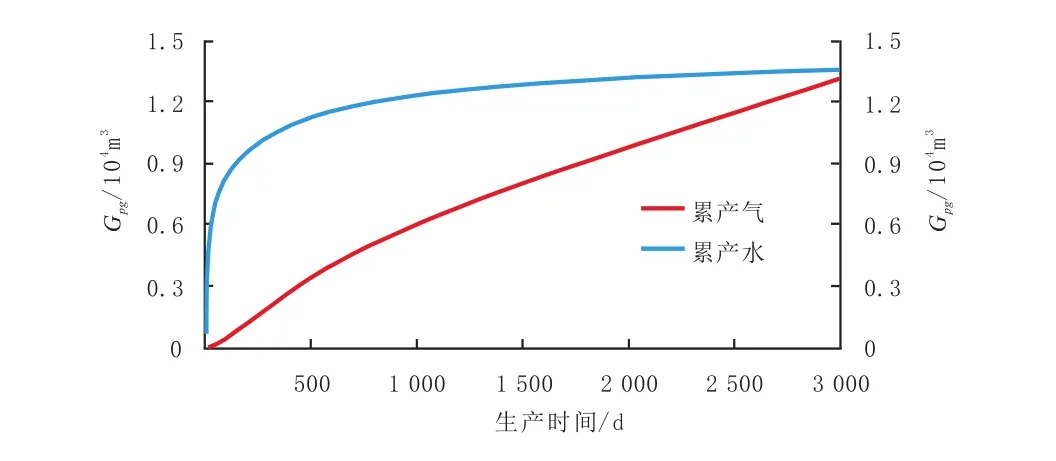
图4 累积产量模拟结果图
4 结论
建立了反映煤层气解吸、扩散及渗流过程的气、水两相耦合流动三维数学模型,给出了数值求解的方法,利用二维交替隐式求解实现了数值模拟计算,该方法计算稳定,收敛速度快。采用上述数值模拟模型编制了煤层气多分支水平井数值模拟软件,利用沁水盆地某试验井进行了模拟计算,与其他模型对比,算例的模拟结果是合理的,证明了模型及其算法的正确性。
[1]张冬丽,王新海.煤层气羽状水平井开采数值模拟研究[J].煤田地质与勘探,2005,33(4):47-51.
[2]张冬丽,王新海.煤层气单井开采数值模拟研究[J].江汉石油学院学报,2004,26(1):76-77.
[3]同登科,张先敏.致密煤层气藏三维全隐式数值模拟[J].地质学报,2008,82(10):1428-1431.
[4]张亚蒲.煤层气数值模拟技术应用研究[D].北京:中国科学院渗流力学研究所,2006.
[5]KhalidAziz,AntioninSettari.油藏数值模拟[M].北京:石油工业出版社,2004.
[6]谢学恒,秦学成.煤层气井见气时间预测方法及其应用[J].煤矿开采,2013,18(4):5-9.
[7]张海茹,李昊.煤层气峰值产量拟合及产量动态预测方法研究[J].岩性油气藏,2013,25(4):116-118.
(编辑:李臻)
A
2095-1132(2014)01-0030-04
10.3969/j.issn.2095-1132.2014.01.009
2013-10-30
2014-01-14
国家科技重大专项项目“大型油气田及煤层气开发”(编号:2011ZX05047)。
陈林(1983-),工程师,从事复杂天然气藏开发技术与理论研究工作。E-mail:chenlinpost@petrochina.com.cn。

