基于模糊控制的异步电动机直接转矩控制系统研究

周贤娟，冯梅琳，韩树人

（江西理工大学机电工程学院，江西赣州341000）

基于模糊控制的异步电动机直接转矩控制系统研究

周贤娟，冯梅琳，韩树人

（江西理工大学机电工程学院，江西赣州341000）

针对传统的异步电动机直接转矩控制中存在低速运行时电动机转矩脉动较大的问题，提出了一种基于模糊控制的直接转矩控制系统模型.该模型采用三输入单输出的结构，将磁链相位角、磁链幅值误差和转矩误差作为模糊变量，并对其进行模糊分级，以此达到优化空间电压矢量选择的目的.并在Matlab/simulink中进行仿真，结果表明该方法有效的减小了转矩脉动，同时有更好的速度响应.

模糊控制；直接转矩控制；转矩脉动；异步电动机

0 引言

直接转矩控制系统具有动态响应快、控制简单等优点.但是传统的直接转矩控制只考虑转矩和磁链误差的方向，根据磁链和转矩输入滞环比较器输出结果，决定逆变器的开关状态.这种方式忽略了转矩和磁链的误差大小，造成转矩和磁链超过滞环带宽范围，导致异步电动机在运行过程中产生较大转矩脉动[1].

针对直接转矩控制转矩脉动大的问题，近年来许多学者提出了改进算法.文献[2-3]利用多电平输出型变换器来减小转矩脉动，多电平逆变器输出增加了电压矢量，可以构成多种形式的开关矢量表，为空间电压矢量的优化选择提供了很大的余地，但是采用新型逆变器在输出更多电压矢量的同时，也使得系统所采用的功率管数量增多，导致系统的成本增加，增加了功率损失，系统可靠性降低.文献[4-6]使用预测控制减小转矩脉动，但是在转矩变动巨大的情况下，会产生巨大的计算量，同时在有巨大的转矩变化的情况下，不能有快速的转矩响应.文献[7-8]使用基于Deadbeat的控制方案，控制定子磁链幅值与转矩.但是使用这种方案，导致坐标变换更加复杂，同时要求更准确的电机参数，这样就降低了系统的稳定性.

文中在不改变传统直接转矩控制简单结构的基础上，使用模糊控制器替代传统直接转矩控制中的滞环比较器，模糊控制器不需要被控系统的精确数学模型，根据已有的经验制定出控制规则，达到有效控制系统的目的.Matlab/simulink仿真结果表明优化的控制策略提供了更快的动态响应，同时减小了转矩脉动.

1 传统直接转矩控制基本原理

在传统DTC控制中，将空间等分为6个扇区，输出电压矢量如图1，其中非零向量u1（100）、u2（110）…u6（101），相位差为60°.零向量u7（111）、u0（000）.电压矢量的输出由滞环比较器及定子磁链角所在扇区决定，结果如表1.

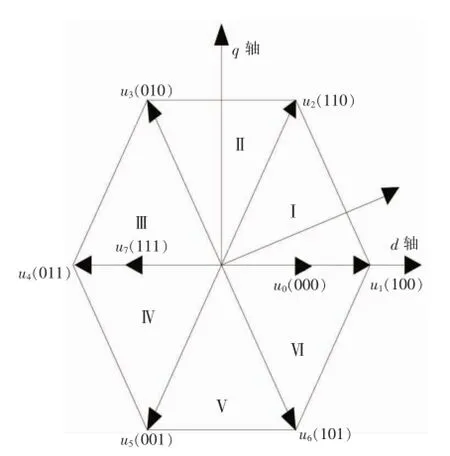
图1 输出电压矢量图

表1 输出电压开关表

2 基于模糊控制的直接转矩控制系统

在直接转矩控制策略中引入模糊逻辑，将定子磁链幅值误差、转矩误差和磁链角度进行的模糊分级，优化开关表，达到更准确选择电压空间矢量的目的[11-13].模糊模型的直接转矩控制的原理图如图2所示.

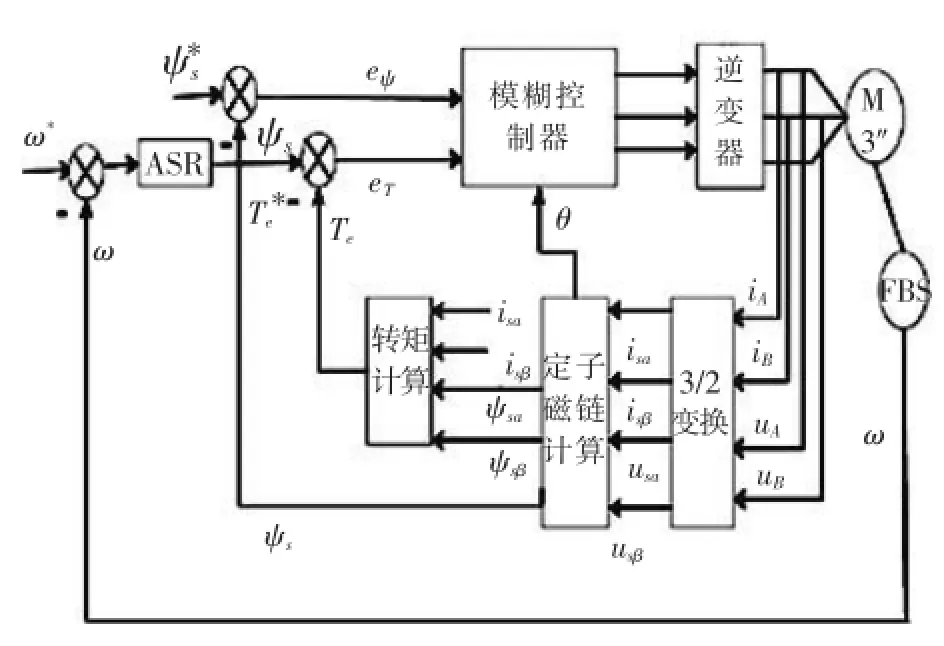
图2 模糊直接转矩系统结构图

2.1 模糊控制器设计

设计的模糊控制器为多输入单输出结构，采用三维输入，一维输出，输入量为eψ、eT以及磁链角θ，输出量为逆变器的开关状态.eψ、eT分别模糊化为Eψ、ET、.Eψ在论域上被分为3个模糊集{P(正)、Z(零)、N(负)}，ET在论域上被分为5个模糊集{PL(正大)、P(正)、Z(零)、N(负)、NL(负大)}，Θ的论域为[-π/ 6,11π/6]，在2π区间等分为π/6的十二个区间.如图3.它们的隶属函数分布分别如图3（a）、3（b）、3（c）所示.因逆变器输出为8个电压空间矢量，所以可以将模糊控制器的输出为离散点，直接将他们分为8个离散模糊子集{u0、u1、u2、u3、u4、u5、u6、u7}，其隶属函数如图3（d）所示.

2.2 模糊控制规则及推理

模糊规则基于已有的控制经验，根据图1所给的电压空间矢量图及扇区位置，定子磁链ψs逆时针旋转，在图1中所给位置时，电压矢量u6、u1、u2使磁链幅值增大，电压矢量u3、u4、u5使磁链幅值减少.当Eψ＝P时，需增大磁链幅值，可以选取电压矢量u6、u1、u2.当Eψ＝Z时，保持磁链幅值不变时，可取电压矢量u0、u7.当Eψ＝N时，需减小磁链幅值，可以选取电压矢量u3、u4、u5.同时u2、u3、u4电压矢量增大转矩，u1，u6，u5将使转矩减小，电压矢量u0、u7不改变转矩.综合磁链与转矩实际情况推出所需电压矢量.同理推得另外11区间.即可得完整的模糊控制表.共含180条规则.如表2.

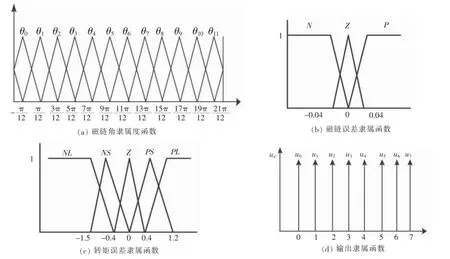
图3 输入输出隶属函数分布图

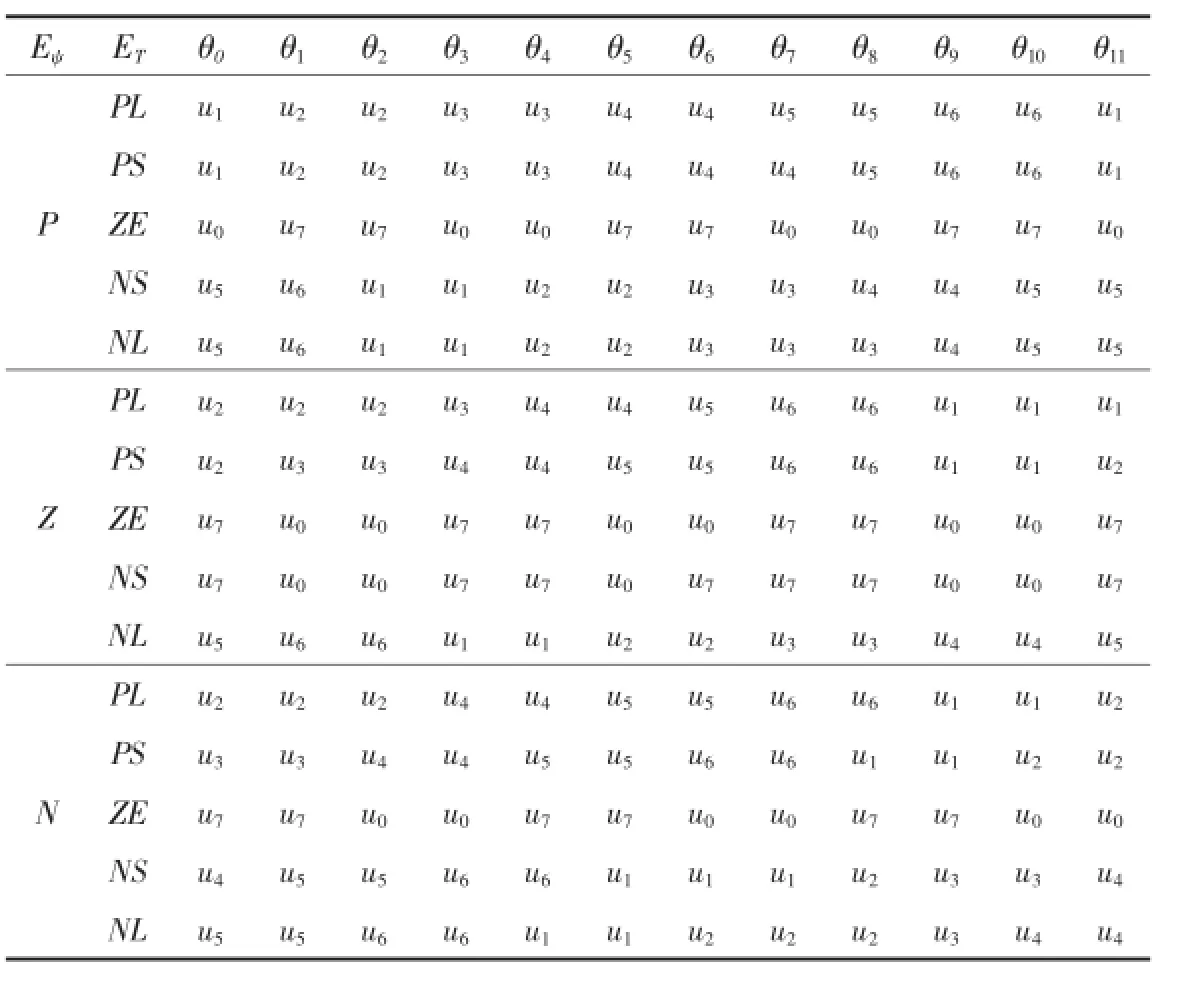
表2 模糊规则表

控制中采用的模糊推理规则为Ri:ifψ=A and ET=B andθ=θjthen U=uk式中A，B，θj，uk为磁链误差、转矩误差、磁链角以及电压空间矢量的子集变量，i=1～180，j=0～11，k=0～7.

模糊推理采用Mamdani模糊推理法，其输出隶属函数为：

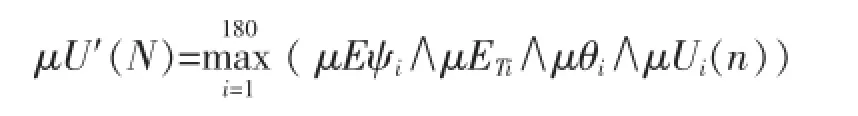
式中μEψi、μETi、μθi分别为Ai、Bi、θi的隶属度；μUi（n）为开关量的输出的隶属度.“∧”为Mamdani的“取小”算子.取最大隶属度对应的输出量为逆变器的开关量输出.

3 系统仿真及分析

选用的电机参数为：三相异步电动机，Rs= 0.435Ω，Ls=0.005 H，Rr=0.816Ω，Lr=0.002 H，Lm= 0.069 H，np=2，J=0.18 kg·m2，F=0.1·N·m·s，ψs=0.3 Wb，额定运行频率fn=60 Hz，电机额定功率Pn=1.5 kW，额定线电压为220 V.传统模型选用Matlab中simulink自带的传统DTC模型作对照.传统DTC模型使用simulink自带默认参数.

图4分别为传统DTC模型与改进后的引入模糊控制的DTC模型的定子磁链轨迹.从图中可以看出模糊控制下的磁链控制相对于传统的DTC控制更加准确.

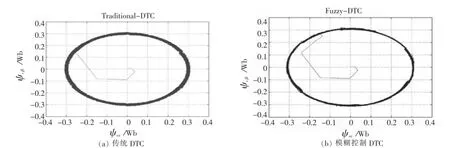
图4 两种控制磁链轨迹图

图5中分别为采用传统DTC模型与模糊控制的DTC模型的转矩曲线.由图5可以看出模糊控制下的DTC模型的转矩脉动相对于传统DTC有所减小.传统模型的转矩脉动范围从图中可以看出大于2 N·m，模糊DTC的转矩脉动小于2 N·m.模糊直接转矩控制转矩脉动范围小于传统DTC.

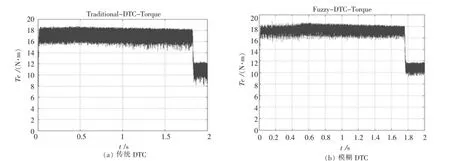
图5 两种控制转矩脉动图

图6 两种控制转速响应图

图6中分别为采用传统DTC模型与模糊控制DTC模型在突加负载后转速响应情况.在0.5 s处加入10 N·m的负载.在转速环ASR调节器的PI值相同的情况下.从转速的跟踪情况可以看出，模糊控制DTC模型的响应速度优于传统的DTC模型.传统DTC到达额定频率的时间为1.82 s.模糊DTC系统达到额定频率的时间为1.77 s.

图7中分别为采用传统DTC模型与模糊控制的DTC模型的电流谐波分析.传统DTC与模糊DTC到达额定频率时间分别为1.82 s与1.77 s.在传统DTC控制下，电机在额定频率下运行的谐波百分比为27.42%，在模糊DTC控制下的电机运行谐波百分比为12.47%.相对于传统DTC控制下的电机，谐波有明显好转.

图7 两种控制下的谐波分析

4 结论

以异步电动机为研究对象，针对传统异步电动机DTC系统转矩脉动较大的问题，提出了一种使用模糊控制器替代滞环比较器的控制方法.并在Matlab中搭建基于模糊控制器的DTC系统的仿真平台，通过仿真表明该方案与传统DTC模型相比，提高了系统性能，转矩脉动和转速响应以及谐波百分比均优于传统DTC.

[1]刘亚东，吴学智，黄立培.改善直接转矩控制性能的SVPWM方法[J].清华大学学报(自然科学版），2004，44（7）:869-872.

[2]杨甫,许伯强,杨桂兰.变频器供电下异步电动机转子断条故障仿真研究［J］.机电工程技术,2009，38（1）:67－69．

[3]魏欣,陈大跃,赵春宇.基于模糊空间矢量调制的直接转矩控制方案[J].系统仿真学报,2007,19（6）:1281-1283.

[3]WAHAB H F A,SANUSI H.Simulink model of direct torque control of induction machine［J］．American Journal of Ap-plied Sciences, 2008,5（8）:1083-1090．

[4]Lee K B,Song J H,Choy I,et al.Torque ripple reduction in DTC of induction motor driven by three-level inverter with low switching frequency[J].IEEE Transactions on Power Electronics, 2012,17（2）:255-264.

[5]Buja G S,Kazmierkowski M P.Direct torque control of PWM inverter-fed AC motors-a surve［J］．IEEE Trans．on Industrial Electronics,2004,51（4）:744-757．

[6]袁登科,陶生桂.一种感应电机直接转矩控制系统性能改善方案［J］.中国电机工程学报,2005,25（8）:151-155.

[7]Rodríguez J,Pontt J,Kouro S,et al..Direct torque control with imposed switching frequency in an 11-level cascaded inverter[J]. IEEE Transactions on Industrial Electronics,2004,51(4):827-833.

[8]Geyer T,Papafotiou G,Morari M.Model predictive direct torque control,Part I:concept,algorithm,and analysis[J].IEEE Transactions on Industrial Electronics,2009,56（6）:1894-1905.

[9]Papafotiou G,Kley J,Papadopoulos K G,et al Model predictive direct torque control,Part II:implementation and experimental evaluation[J].IEEE Transactions on Industrial Electronics,2009,56（6）:1906-1915.

[10]杨赛，任金霞.改进型模糊控制器在工业过程中的应用[J].江西理工大学学报，2009，30（4）：26-28.

[11]Beerten J,Verveckken J,Driesen J.Predictive direct torque control for flux and torque ripple reduction[J].IEEE Transactions on Industrial Electronics,2010,57(1):404-412.

[12]Kenny B H,Lorenz R D..Stator and rotor flux based deadbeat direct torque control of induction machines[J].IEEE Transactions on Industry Application,2010,39(4):1092-1101.

[13]Yan Shu,Xiao Jian.Deadbeat direct torque control of induction motor[J].Electric Machines and Control,2007,11(2):125-129.

Research on the direct torque control system of asynchronous motor based on fuzzy control

ZHOU Xian-juan,FENG Mei-lin,HAN Shu-ren
（School of Mechanical and Electrical Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China）

In the direct torque control of traditional asynchronous motor,there lies a big problem of its ripple when itis running at a low speed.Hence a model is put forward of direct torque control based on fuzzy control. The modeladopts the structure of the three inputs and single output with the flux linkage phase angle and flux linkage amplitude error and the torque error as fuzzy variables.Fuzzy classification is also used for them to achieve the goal of optimization of space voltage vector selection.And Matlab/simulink is used in the simulation.The results show that this method effectively reduces the torque ripple,and at the same time a better speed in response can be achieved.

fuzzy control;direct torque control;torque ripple;asynchronous motor

TP89

A

2095-3046(2014)03-0051-05

10.13265/j.cnki.jxlgdxxb.2014.03.010

2014-04-03

江西省教育厅基金项目（GJJ10480）;国家大学生创新创业训练计划项目（201210407027）

周贤娟（1981-），女，讲师，主要从事网络化测控等方面的研究，E-mail：106807854@qq.com.