还注采舌进图一个理论基础
齐成伟
(重庆科技学院,重庆 401331)
还注采舌进图一个理论基础
齐成伟
(重庆科技学院,重庆 401331)
运用平面稳态流速场运动学通式,经过“求逆,求导,求积”3步运算,获得了无限大等厚均质水平地层内等流量一注一采两口铅垂井激发的渗流场内流体质点的运动学方程。根据所得方程,首次从理论上成功地绘制了注采舌进图,填补了现行油气渗流力学教科书中的理论空白。该通式还可用于求解铅垂井群或裂缝群注采相关的运动学问题,因而可作为水驱油技术的重要理论基础。
流体力学 流体运动学 渗流力学 渗流运动学 水驱油技术 舌进现象 时变方程 教学改革
0 引言
注采舌进图[1]没有理论基础却未被油气渗流力学教科书[2-10]舍弃,说明舌进现象非常重要。
要迅速准确地绘制流体运动图像,须用理论数学实现流体运动学的Lagrangian描述(下称“拉氏描述”)。但如University of Cambridge的Batchelor教授所言,“it leads to rather cumbersome analysis(拉氏描述会带来相当麻烦的分析困难)…”[11];或如University of Michigan的Potter博士所言,“This becomes,however,a difficult task(实现拉氏描述是项艰难的工作)…”[12]。
为揭露舌进现象的本质,笔者历时5年,在平面稳态流速场(下称“平稳场”)内实现了拉氏描述,发表了平稳场运动学通式[13]。
1 基础准备
1.1 平稳场运动学通式
平稳场(含忽略油水流度差异的渗流场)内流体质点的运动学通式:
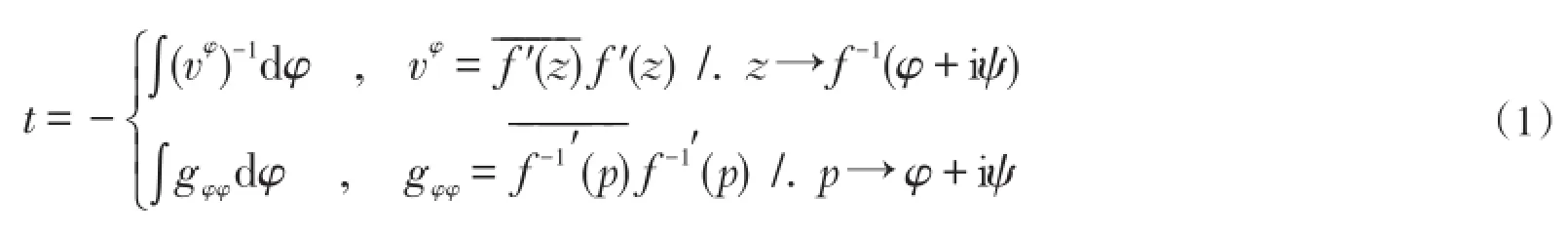
式(1)中,p=f(z),p=φ+iψ,z=x+iy。若式(1)中的被积函数不存在有限形式的原函数,则采用Gauss型求积公式。
1.2 场的复位势
无限大等厚均质水平地层内环形井群激发的渗流场的复位势通式[14]为:
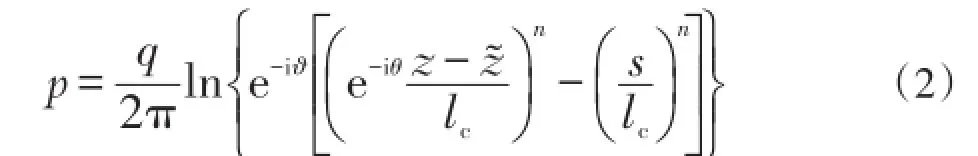
式(2)中,q为每口铅垂井在单位厚度地层内的流量,m2/s;ϑ为相位角,rad;θ为任一井绕井群形心逆时针偏离实轴正向的角度,rad;n为环形井群的井口数;s为环形井群的成圆半径,m;lc为特征长度,m。
令q=-|q|且n=1并做替换θ→θ+π得到一口注入井的复位势;令q=|q|且n=1得到一口位置与注入井关于点对称的采出井的复位势。取ϑ=π,运用复势叠加原理得到注采井的复位势:
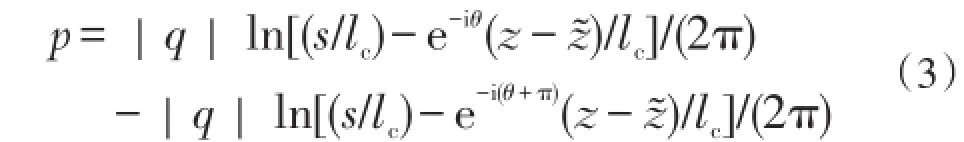
2 运动学方程
据平稳场运动学通式,仅需“求逆,求导,求积”3步运算,便可获得运动学方程。
式(3)的逆函数为:

复变函数求导法则与实变函数的相同,有:
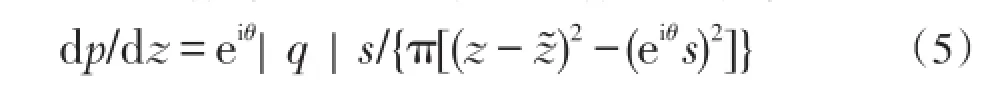
将式(4)和式(5)代入式(1),得到以势流坐标表示的流速的逆变分量:
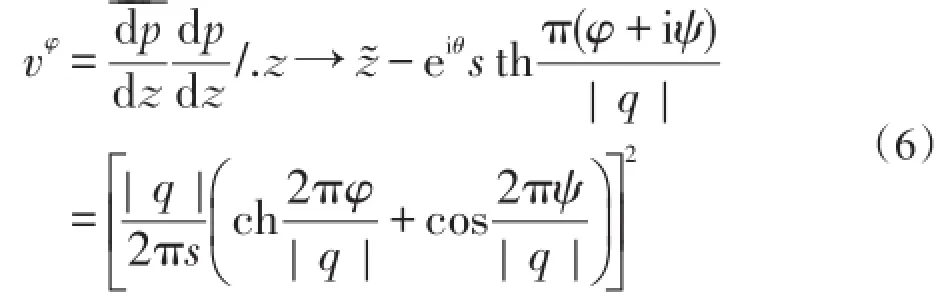
将式(6)代入式(1),积分后得到以势流坐标表示的运动学方程:
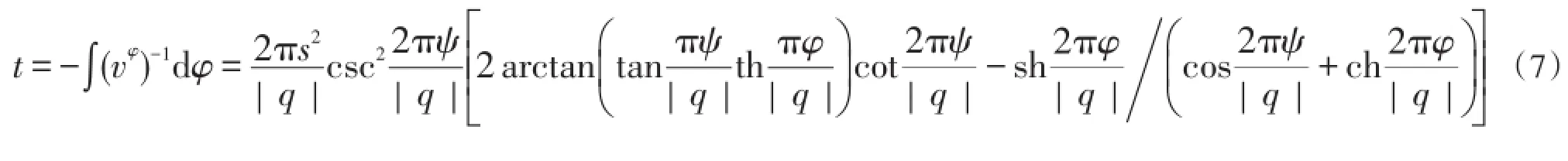
显然,式(7)以被跟踪流体质点流经势为0的等势线(即两井连线的中垂线)的时刻为0时刻。被跟踪流体质点流经井位处的时刻为:
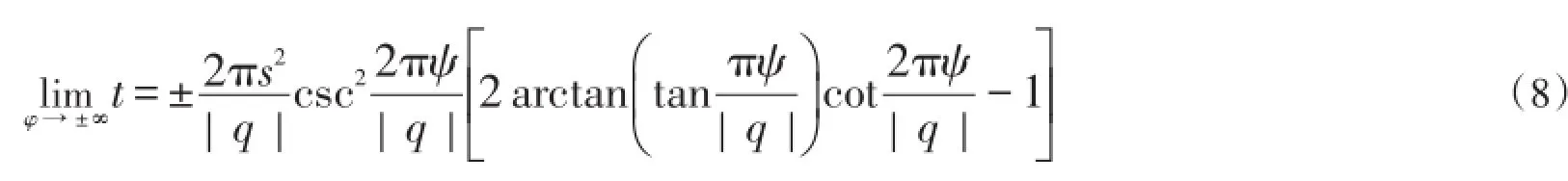
将被跟踪流体质点离开注入井进入地层的时刻标定为0,则运动学方程为:

在流线ψ=|q|/2上,所得方程照顾不到,但不影响绘图。
3 图像绘制
3.1 注采舌进图
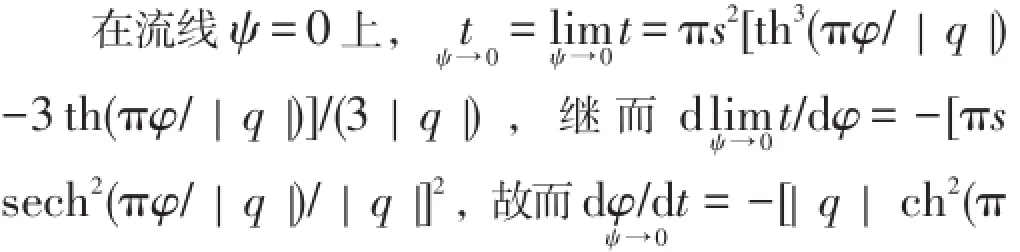
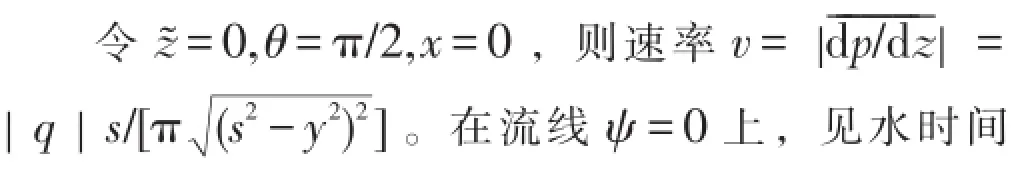

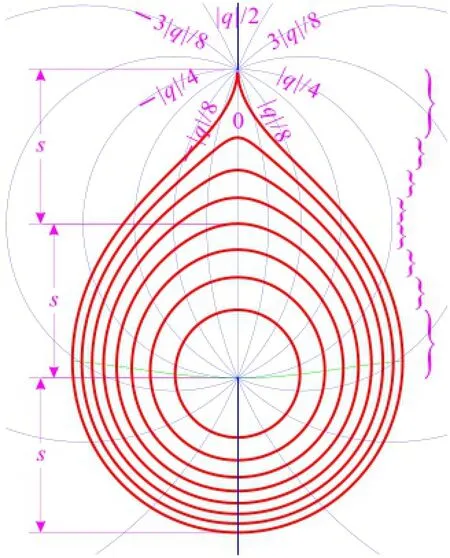
图1 注采舌进图
3.2 偏心舌进图
(2πϕ/|q|)的圆形等压供液边界地层内一口偏心率e=e2πϕ/|q|的采出井激发的渗流场内流体质点的运动图像(图2)。见水时间:-th3(πϕ/|q|)]/(3|q|)。若r,ϕ已知,则对于选定的e,有s=r(1-e2)/(2e),|q|=2πϕ/lne。易知,波及系数为(1-e)2(3+e)/[3(1+e)]。
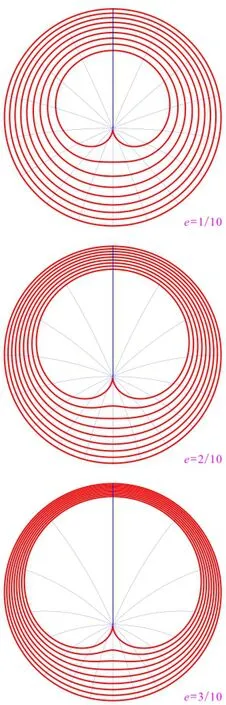
图2 偏心舌进图
4 结束语
平稳场运动学通式在注采舌进图的绘制上取得了成功,展示了理论的简捷魅力。笔者认为平稳场运动学通式具有如下意义和价值,诚邀流体力学和渗流力学界的教育和科研工作者探讨争鸣。
1)理论意义:弥补流体力学基础理论的不足,完善流体力学和渗流力学教科书。
2)工程价值:结合黏性指进现象解释油水界面的移动和变形规律,为注采井网的设计和见水时间的预计提供渗流运动学依据。
[1]R. E. Collins,L. H. Simons. Calculation of water-flood sweep patterns for unit mobility ratio[C].SPE-200-MS,1961:1-29.
[2]葛家理.现代油藏渗流力学原理(上册)[M].北京:石油工业出版社,2003:104.
[3]孔祥言.高等渗流力学(第2版)[M].合肥:中国科学技术大学出版社,2010:96.
[4]程林松.高等渗流力学[M].北京:石油工业出版社,2011:29-30.
[5]张建国,杜殿发,侯健,等.油气层渗流力学(第2版)[M].东营:中国石油大学出版社,2009:87-88.
[6]李晓平.地下油气渗流力学[M].北京:石油工业出版社,2008:71.
[7]翟云芳.渗流力学(第3版)[M].北京:石油工业出版社,2009:30.
[8]李璗,陈军斌.油气渗流力学[M].北京:石油工业出版社,2009:59.
[9]徐献中.石油渗流力学基础[M].武汉:中国地质大学出版社,1992:130-134.
[10]冯文光.油气渗流力学基础[M].北京:科学出版社,2007:148-149.
[11]George K. Batchelor. An Introductionto Fluid Dynamics[M]. England: Cambridge University Press,2000:71.
[12]Merle C. Potter, David C. Wiggert, Bassem H. Rama⁃dan. Mechanics of Fluids(fourth edition)[M].CL-Engi⁃neering,2011:89.
[13]齐成伟.平面稳态流速场运动学通式[J].天然气技术与经济,2013,7(6):27-28.
[14]齐成伟.环形井群激发的渗流场之复分析[J].内蒙古石油化工,2010,36(2):32-35.
(编辑:周娟)
A
2095-1132(2014)03-0034-03
10.3969/j.issn.2095-1132.2014.03.008
修订回稿日期:2014-04-28
齐成伟(1983-),硕士,实验师,从事油气水渗流力学基础理论研究。Email:1261621@qq.com。
时间:2014-05-07网址:http://www.cnki.net/kcms/doi/10.3969/j.issn.2095-1132.2014.03.000.html。

