基于混沌并行差分进化算法的含风电配电网无功优化
何 健,丁晓群,陈光宇,张 杭,邓吉祥
(河海大学能源与电气学院,南京市211100)
0 引 言
风电作为一种新型的分布式发电,将其并入配电网,会对配电网的电能质量和运行方式都会产生一定影响[1-3]。风电场的随机性出力使得传统无功优化模型难以胜任,因此研究含风电机组的配电网无功优化具有重要的理论和实践意义。
文献[4]探讨了我国的风电消纳现状及其输送方式。文献[5]深入研究了双馈异步发电机(doubly fed induction generator,DFIG)的无功调节能力。文献[5]将风电机组同时接入系统,提出了系统场景的划分方法,用于解决含多个风电机组的配电网无功优化问题。文献[6]将直驱式同步风电机组接入电网,研究了其对系统无功电压控制的影响。文献[7]将DFIG 的无功出力作为连续性控制变量参与配电网无功优化,但仅选取了日风速预测曲线中的5个典型风速点进行分析,并不能概括全天风电出力的变化。文献[8]根据日功率曲线将一天平均分为6个时段,每个时段取风电的平均输出功率参与无功优化。这种处理方式较为粗糙,忽视了风电出力的快速变化,其结果很难令人信服。
文献[9]采用分支线路和主馈线相结合对配电网进行无功优化。文献[10]采用模态分析法选取配电网的关键节点作为无功补偿点,提高了系统电压稳定性,减小了搜索空间。文献[11]提出模糊聚类法来搜寻系统中的薄弱节点,进而确定无功补偿的具体个数及相应地点。但上述文献都是在一种假定的确定性运行方式下进行无功补偿选址的,而并未考虑电力系统可能出现的各种运行状态,其适应性不强。文献[12]基于差分进化(differential evolution,DE)算法对配电网进行无功优化,但存在早熟、易陷入局部最优的缺点。
综上,国内外在处理含DFIG 的配电网无功优化时,在其无功补偿选址很少对电网运行方式的不确定性进行研究。为此,本文运用蒙特卡罗仿真来考虑系统可能出现的各种运行状态及其概率,为无功补偿选址提供理论依据。针对风电场出力的随机性,采用场景分析法将随机性无功优化问题转化为多个场景的确定性问题来处理。针对DE 存在的缺点,采用带反馈的混沌并行差分进化算法(chaotic parallel differential evolution algorithm with feedback,CPDEF)来求解配电网无功优化。
1 含DFIG 的配电网场景分析
风速的间歇性和随机性使得含风电机组的配网无功优化成为随机性问题。为此,本文采用场景分析法[13]将其不确定性因素转变为多个确定性场景来处理,从而避免建立复杂的随机性模型。
影响DFIG 输出功率的风速曲线满足Weibull 分布,即
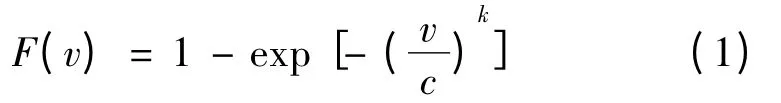
式中:v 为风速;k、c 分别为Weibull 分布的形状参数和尺度参数,本文分别取2.0 和8.5。
DFIG 输出功率Pw和风速v 的函数关系为

式中:k1= Pr/(vr- vci);k2= - k1vci;Pr为DFIG 额定输出有功功率;vci、vr、vco分别为切入风速、额定风速和切出风速。据此,可将DFIG 的输出功率模式分为3 种典型场景:场景I、II、III 分别对应零输出状态、欠额定输出状态和额定输出状态,其各自的场景概率p1、p2、p3分别为
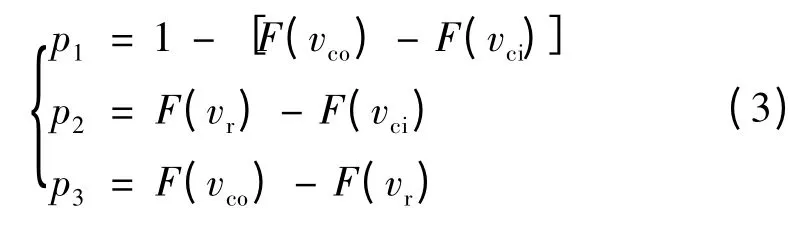
零输出场景功率Psw1和额定输出场景功率Psw3分别为0 和Pr。欠额定输出场景功率Psw2取该场景下输出功率的期望值

在每一种典型场景下,DFIG 发出的有功功率Pw与无功功率Qw的关系表达式为

式中:Us、Is、Xs分别为定子侧电压、绕组电流和漏抗;s为转差率;Xm为励磁电抗;Ir为转子侧变流器电流[14]。
2 含DFIG 配电网无功优化场景模型
2.1 目标函数
本文从系统网损、电压波动两方面来衡量含DFIG 的配电网无功优化策略的优劣,通过构造各自的隶属度函数[15],最后将二者加权求和作为目标函数,以此作为满意度来进行评价。
(1)系统网损Ploss的隶属度函数

式中:Ploss为无功优化后的网损;Plmax为最大允许网损,即无功优化前的网损;Plmin为理想网损,即在当前负荷和DFIG 出力下,有足够的无功源进行线路补偿,仅由有功功率传输所造成的最小网损。
(2)电压波动ΔUi的隶属度函数
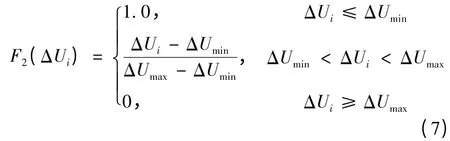
式中:ΔUi为节点i 电压波动的绝对值;ΔUmax、ΔUmin分别为系统所允许电压波动的上、下限,国家标准规定分别为ΔUmin=0.012 5,ΔUmax=0.04[16]。
(3)综合目标函数

式中:λ1、λ2为权重系数,本文取λ1= 0.95,λ2= 0.05。
2.2 潮流方程约束
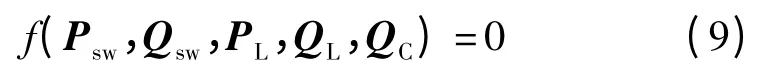
式中:Psw、Qsw、PL、QL、QC分别为系统场景有功功率、场景无功功率、有功负荷、无功负荷和无功功率补偿向量。
2.3 变量约束
(1)控制变量不等式约束

式中:Timax、Timin、QCimax、QCimin、Qswimax、Qswimin分别为节点i 有载调压变压器变比、无功补偿容量和风电场景无功功率的上、下限。
(2)状态变量不等式约束
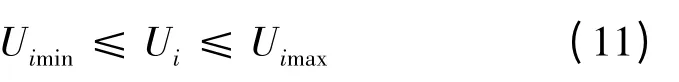
式中:Uimax和Uimin为节点i 的电压上、下限值。
3 无功补偿选址
电力系统无功补偿选址是对系统未来运行方式下无功补偿设备分布的安排,而系统的运行方式却是不确定的,因此在任何特定的系统状态下进行的无功规划都是不合理的。本文采用蒙特卡罗[17]方法将系统的各种随机因素都考虑在内,对系统运行状态的不确定性进行仿真。
蒙特卡罗抽样方法的基本思想:建立一个关于配电网运行方式的概率模型,使其状态参数等于所求问题的解,通过对其模型的抽样试验来求解待求参数的统计特性。在配电网中,变压器、线路和负荷的数目很多,在一定的负荷水平下,线路和负荷可能有多种组合,为进行无功补偿选址,需对数千种运行方式进行研究。
首先,产生服从均匀分布的伪随机数,按照系统中各元件故障率的大小随机抽样以确定各元件的运行状态,进而确定系统的运行状态。然后,对系统进行潮流计算,得到该运行状态下各节点电压的分布情况,若某些节点出现电压越限,则对其进行无功补偿,进而将蒙特卡罗抽样与无功优化相结合。最后,统计各项指标。其统计指标为:(1)节点电压平均值=;(2)补偿概率η = 补偿次数/n[17]。
为保证配电网的安全运行,对其不同的故障运行模式,需在不同的节点安装无功补偿设备,但不能随意地增加无功补偿。为此,本文对配电网进行运行状态概率抽样试验,编写相关程序,找出最需要无功补偿的节点。其程序主流程为:(1)系统状态抽样,进行潮流计算;(2)判断系统各节点电压水平是否满足要求,是则返回步骤(1),否则继续;(3)对不满足电压安全水平的节点进行无功补偿,并计算其无功补偿次数;(4)统计系统各节点无功补偿概率,输出结果。
4 混沌并行差分进化算法
4.1 差分进化算法
差分进化算法[12]的步骤为:
(1)种群初始化。设种群规模为NP,种群中第i代的n 维个 体j 表 示 为Xi,j=[xi,j,0,xi,j,1,…,xi,j,n],则第0 代的第k 维个体i 初始化为
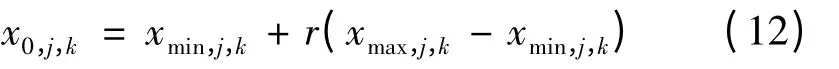
式中r 为取值范围为(0,1)的随机分布数。
(2)变异操作。对于第i 代个体,从当代种群中随机选取3个不同个体,经变异操作产生试验向量

式中变异因子F ∈[0,1],控制偏差变量的缩放。
(3)交叉操作。为了保持种群的多样性,通过交叉操作,产生试验向量Ui+1,j,则有

式中:rn∈[1,2,…,n]为一随机整数,以保证向量至少有一维变异变量;CR∈[0,1]为交叉概率,是一个预先设定的常数。
(4)选择操作。利用基于贪婪思想的一对一选择操作
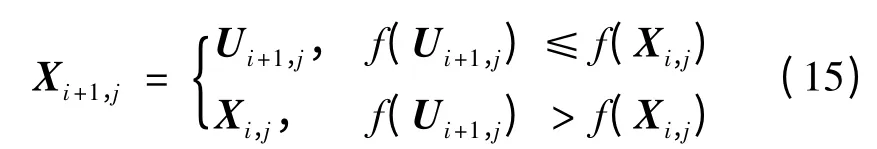
DE 特有的进化操作使其具有较强的鲁棒性、优化结果与初始值选取无关、优化过程中所需控制量较少等优点,但也存在易“早熟”而陷入局部最优、全局搜索能力不强的缺点。为此,本文利用混沌映射系统的优良特性来保持群体的多样性,从而防止算法出现“早熟”现象;采用Baldwin 效应的强化学习模式,克服了DE 搜索的盲目性和随机性,进而加快其收敛速度。
4.2 混沌映射
采用混沌映射中的一种不可逆映射,即Logistic映射I:(0,1)→(0,1),来更新变量xi+1= axi(1 -xi),xi∈[0,1]。其中:i = 1,2,…,n;a 为参数。利用混沌系统的遍历性、伪随机性和极端敏感于初始条件等特性来设计和保持群体多样性,提高算法全局搜索能力。
4.3 基于Baldwin 效应的强化学习
在生物学中,个体在其生命周期中能够进行自适应学习的现象称为Baldwin 效应。使得生物个体能够不完全依赖于基因的遗传,而通过后天学习来克服基因中“缺失”或“次优”的特性,从而增强整个群体的生存能力。
在CPDEF 算法中,对所有新个体都进行强化学习。对于新一代个体x = (x1,x2,…,xn),用广义进化偏导数∂f(x)/∂xi来表征其演化过程中的反馈信息。基于该反馈信息,个体x 进行强化学习:
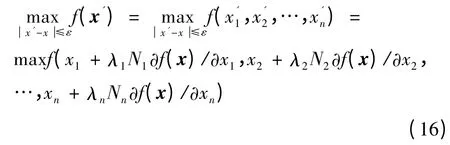
即对个体x 的每个xi∈[xL,xR],以∂f(x)/∂xi作为强化学习方向,λiNi为学习步长;λi= (xR-xL)/T,T 为迭代次数,以确保x'i位于可行域[xL,xR]中;Ni∈Z +初始值都为0,并采取变尺度搜索策略,以便搜索到局部最优解;经过强化学习后,新个体的适应度会得到普遍提高。
直接从进化过程中提取出进化偏导数,刻画出个体的正确进化方向,以此来模拟生物系统继承和处理反馈信息的能力,进而克服了传统DE 搜索算法的盲目性和随机性,加快了收敛速度。
4.4 基于CPDEF 算法的无功优化步骤
(1)输入配电网相关参数、负荷、有载调压变压器档位数及步长、投切电容器容量及其组数、电压上下限,风电场的相关运行参数、风速,并计算其有功功率输出及其无功调节范围。
(2)初始化种群。设迭代次数K =0。
(3)应用Logistic 映射对种群进行混沌优化,避免其陷入局部最优,增强其全局搜索能力。
(4)通过变异、交叉产生新一代种群。
(5)基于Baldwin 效应对所有新生代个体执行强化学习,提高其收敛速度。
(6)潮流计算其适应度值。判断适应度值是否达到规定精度或迭代次数是否达到最大迭代次数,是则停止;否则K =K +1,转步骤(3)。
5 算例分析
采用如图1 所示的含风电机组的IEEE 33 节点系统进行测试和分析,以验证所提出无功优化模型和算法的正确性和有效性。电压基准值取12.66 kV,功率基准值取10 MVA。

图1 IEEE 33 节点测试系统Fig.1 IEEE 33-bus test system
图1中节点1 处有载调压变压器的电压调节范围为0.95 ~1.05,共有9个档位,步进量为1.25%。在33 节点接入由2 台1.5 MW 变速恒频DFIG 组成的风电场。CPDEF 算法的参数:种群规模NP=50,变异因子F = 0.5,交叉概率CR= 0.5,迭代次数K =50。
5.1 基于CPDEF 算法的无功优化步骤
对IEEE 33 节点系统进行蒙特卡罗仿真计算,进行10 000次抽样,所得系统各节点无功补偿概率统计结果如表1 所示。
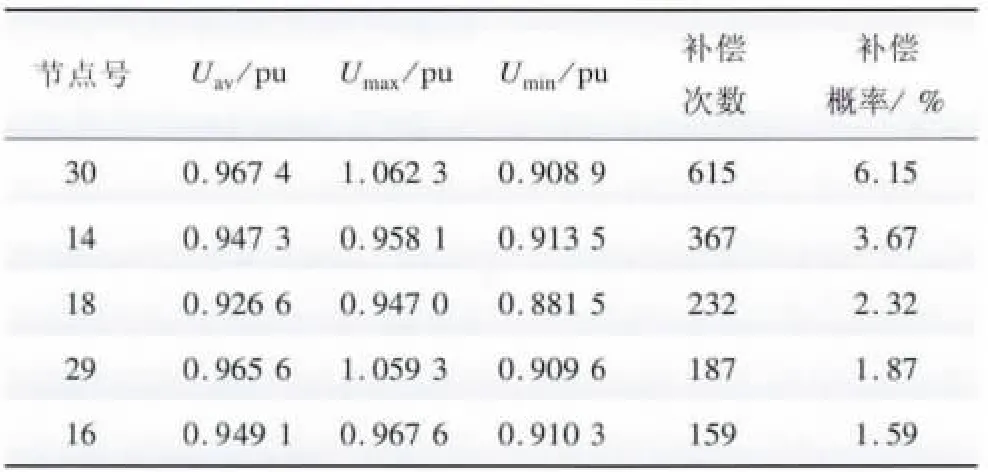
表1 含风电场IEEE 33 节点系统无功补偿统计结果Tab.1 Statistical results of reactive power compensation for IEEE 33-bus system with wind farm
由表1 可知,节点30、14 的补偿概率最大,即这2个节点最易发生电压安全问题,需要无功补偿的可能性最大。因此在财力有限的条件下,从系统全局的电压安全水平考虑,在这些节点安装无功补偿设备将取得最佳的补偿效果。为此,在节点14 和30 处各安装可投切并联电容器5 组和10 组,每组容量为100 kvar。
5.2 基于场景分析的含风电场配电网无功优化
DFIG 的vci、vr、vco分别为3,13.5,20 m/s。选取风电场的3 种典型运行场景:(1)零输出场景;(2)欠额定输出场景;(3)额定输出场景。各场景输出功率分别为0,0.75,1.5 MW,其无功功率调节范围分别为:[-0.485 5 Mvar,2.325 8 Mvar]、[-0.485 5 Mvar,1.561 2 Mvar]和[-0.485 5 Mvar,1.264 4 Mvar]。按式(3)计算可得各场景概率分别为0.121 1,0.802 6,0.076 3。基于CPDEF 算法,在未考虑和考虑DFIG无功调节能力的情况下,其场景无功优化结果分别如表2、3 所示。表中:T 为OLTC 分接头位置;C1、C2分别为投入节点14 和30 处的并联电容器组数;UPCC为风电场并网点电压;F 为满意度,即目标函数值。
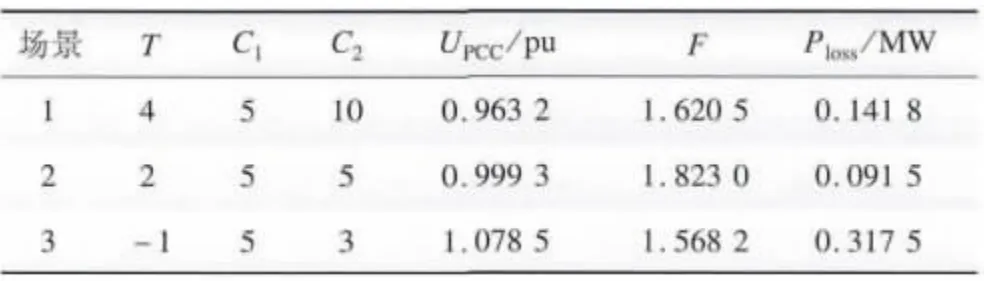
表2 未考虑DFIG 无功调节的场景无功优化结果Tab.2 Optimal results of scenario reactive power without considering reactive power of DFIG
根据F 的各子目标函数值,分别进行去模糊化处理,经计算得到系统网损Ploss和各节点电压偏移量ΔUi,进而求得各节点电压值Ui。在额定输出场景下,无功优化前后的各节点电压分布如图2 所示。
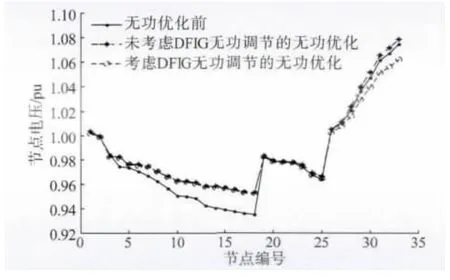
图2 额定输出场景下无功优化前后节点电压比较Fig.2 Voltage comparison before and after reactive power optimization under rated output scenario
在额定场景下,风电场并网点电压为1.077 9 pu,已发生电压越限。此时,投切电容器组已不适用,需额外安装静态无功补偿器(static var compensator,SVC),这必然会产生额外的配置费用。由表2 可知,通过DFIG 吸收无功对并网点进行电压控制,可起到较好的调节系统电压的作用。此外,其无功调节具有连续性,能克服传统配电网无功调压手段调节离散化、调节速度慢、无法实现电压连续调节的缺点。
5.3 CPDEF 算法的有效性验证
为验证CPDEF 算法的有效性,按文献[12]提出的DE 和文献[18]提出的量子差分进化算法(quantum differential evolution,QDE),分别应用于欠额定输出场景下的无功优化,并连续运行50次,最后得到的关于满意度F 的收敛特性曲线如图3 所示。
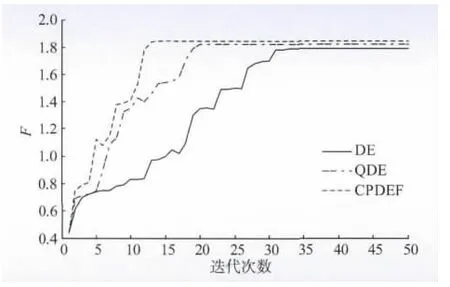
图3 算法的收敛特性曲线比较Fig.3 Comparison of convergent curve for algorithms
由图3 可知,CPDEF 在优化效果与计算速度上较DE、QDE 都有一定的优越性。在适应度函数F 进化初期,曲线陡升,此时混沌算子发挥主要作用,这源于利用混沌系统的遍历性、伪随机性和极端敏感于初始条件等特性来保持群体的多样性。随后,函数曲线细微地增长,学习因子发挥主要作用,此时所有新生个体执行强化学习因子,有效地克服了传统DE 算法的盲目性和随机性,加快了收敛速度。
6 结 论
(1)运用蒙特卡罗仿真来考虑含风电场的配电网可能出现的各种运行状态及其概率,为无功补偿选址提供理论依据,提高了系统电压稳定性,减小了CPDEF 算法的搜索空间。
(2)采用场景分析法将含风电场的配电网随机性无功优化问题转化为多个场景的确定性问题来处理,其无功优化结果综合了3 种典型场景的影响,体现了对DFIG 随机出力的适应性。
(3)CPDEF 克服了DE 早熟、易发生局部最优的缺点,能够更好地获得全局最优解。此外,其计算精度和收敛速度也得以明显提升。
(4)算例分析表明,本文所运用的无功优化求解策略,能够降低系统网损,提高配电网的节点电压水平,保证整个配电网能够的安全经济运行,进而证明了本文所提出无功优化策略的可行性及有效性。
[1]张丽英,叶廷路,辛耀中,等. 大规模风电接入电网的相关问题及措施[J].中国电机工程学报,2010,30(25):1-9.
[2]汪宁渤,马彦宏,王建东.大规模风电集中并网对电力系统安全稳定的影响[J].电力建设,2011,32(11):77-80.
[3]林章岁,罗利群. 福建省风电出力特性及其对电网的影响分析[J].电力建设,2011,32(12):18-23.
[4]郭飞,王智冬,王帅,等.我国风电消纳现状及输送方式[J]. 电力建设,2014,35(2):18-22.
[5]Engelhardt S,Erlich I,Feltes C,et al. Reactive power capability of wind turbines based on doubly fed induction generators[J]. IEEE Transaction on Energy Conversion,2011,26(1):364-372.
[6]De Rijcke S,Ergun H,Van Hertem D,et al. Grid impact of voltage control and reactive power support by wind turbines equipped with direct-drive synchronous machines [J]. IEEE Transaction on Sustainable Energy,2012,3(4):890-898.
[7]赵晶晶,符杨,李东东.考虑双馈电机风电场无功调节能力的配电网无功优化[J].电力系统自动化,2011,35(11):33-38.
[8]段建东,杨杉.基于改进差分进化法的含双馈型风电场的配电网无功优化[J].电力自动化设备,2013,33(11):123-127.
[9]丁晓群,王宽,王斌,等.主馈线和分支线路相结合的配电网无功补偿[J].电力自动化设备,2006,26(4):11-14.
[10]丁晓群,王宽,沈茂亚,等.结合模态分析的遗传算法在配电网无功规划中的应用[J].电网技术,2006,30(17):47-50.
[11]Wang Y R,Li F X,Wan Q L,et al.Reactive power planning based on fuzzy clustering,gray code,and simulated annealing[J]. IEEE Transaction on Power Systems,2011,26(4):2246-2255.
[12]康忠健,訾淑伟.基于差分进化算法的油田区域配电网无功优化技术的研究[J].电工技术学报,2013,28(6):226-231.
[13]陈海焱,陈金富,段献忠.含风电机组的配网无功优化[J]. 中国电机工程学报,2008,28(7):40-45.
[14]Santos-Martin D,Arnaltes S,Rodriguez Amenedo J L. Reactive power capability of doubly fed asynchronous generators[J].Electric Power Systems Research,2008,78(11):1837-1840.
[15]余昆,曹一家,陈星莺,等.含分布式电源的地区电网无功电压优化[J].电力系统自动化,2011,35(8):28-32.
[16]石嘉川,刘玉田.计及分布式发电的配电网多目标电压优化控制[J].电力系统自动化,2007,31(13):47-51.
[17]张瑞华,宋云亭.基于蒙特卡罗仿真和电压安全约束的无功优化算[J].电力系统自动化,2002,26(7):23-27.
[18]马玲,于青,刘刚,等.基于量子差分进化算法的电力系统无功优化[J].电力系统保护与控制,2013,41(17):39-43.

