特高压直流换流变压器励磁涌流及其抑制

余世峰，聂定珍，项 冰

(国网北京经济技术研究院，北京市102209)

0 引 言

在未来相当长一段时间内，中国电力流仍将呈现大规模“西电东送”和“北电南送”的总体格局，北部、西部规划开发的大型水电、火电、风电将主要用于满足中东部地区负荷中心用电需要。中国未来电网承担着将西北、东北、内蒙古西部、四川西部及境外电力输送至中国中东部负荷中心地区的任务，各大能源基地距离中东部负荷中心1 000 ～3 000 km，电网将呈现典型的大容量、远距离输送的特征。根据特高压交直流输电的技术特点，特高压直流定位于大型能源基地的远距离、大容量外送，西南水电基地、西北及新疆等煤电、风电基地和跨国电力等都可以通过直流输送。在±800 kV的基础上选择±1 100 kV 作为特高压直流输电电压等级的补充，输电容量可达到10 000 MW 以上，电压、输电容量级差合理，有利于提高直流输电的规模效益。准东、伊犁煤电基地距离中东部负荷中心较远，为2 700 ～3 700 km，均在±1 100 kV 特高压直流经济输送距离之内，未来10年，准东、伊犁煤电基地将新增外送电力约40 GW，应考虑采用±1 100 kV特高压直流输送到华中东四省(湖北、湖南、河南、江西)及川渝地区。

±1 100 kV 特高压直流输电技术发展的重点和难点在于大容量换流设备的制造及投运后交直流系统的安全稳定运行等方面［1-3］。换流变压器是直流换流器的核心组成部分，随着直流输电电压的提高，单台换流变压器容量进一步增大，短路阻抗进一步上升，其运行特性尤其值得关注。

直流系统启动时，首先需要将系统由极隔离状态转为极连接状态，此过程中，换流阀保持闭锁，实际换流变压器处于空载状态。当换流变压器进行空载合闸操作时，由于变压器铁心磁路饱和，可能出现很大的冲击电流，此电流称为换流变压器励磁涌流。对于换流变压器，若不采取适当的措施，则可能引起变压器保护的误动作，从而导致充电失败，变压器不能顺利的投入工作［4-10］。本文基于±1 100 kV 特高压直流用高压端换流变压器，建立电磁暂态仿真模型研究系统短路容量、合闸电阻以及选相合闸对励磁涌流的影响及抑制作用。

1 换流变励磁涌流机理研究

变压器处于正常运行或外部故障状态下，铁心通常处于不饱和状态，呈现出绕组励磁电感大的特性，励磁电流相对额定电流较小。当变压器空载合闸操作或外部故障切除后，电压恢复过程中，变压器铁心饱和，呈现出励磁电感变小的特性，将产生一个较大的暂态励磁电流，该电流即为励磁涌流。涌流电流通常可达额定电流的数倍，励磁涌流的存在，可能导致变压器差动保护误动［11-13］。

特高压直流工程用换流变压器多采用单相变压器，单相变压器励磁涌流产生与变压器铁心的饱和有关，饱和磁化曲线，如图1［14-15］所示。

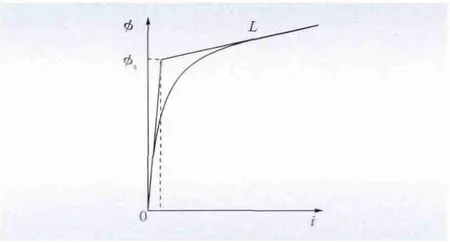
图1 变压器磁化曲线Fig.1 Magnetization curve of transformer

设合闸时，电源电势为E=Umsin(ωt+α)。变压器电源电压按纯正弦，电源内阻不计考虑，则回路中电压与磁通φ 的关系可表达为

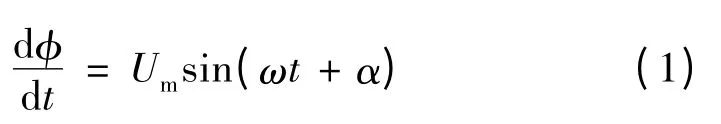
式中:Um为系统电压最大值;t 为时间;ω 为角频率;α为合闸相位角。

变压器空载合闸时，铁心磁通的表达式为

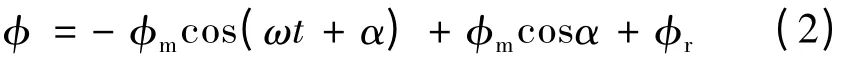
式中:φm为合闸瞬间电压在铁芯中建立的磁通的最大值;φr为剩磁通。

t0时刻合闸，令合闸初相角α =0，则上式化为

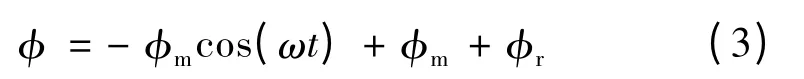
当ωt =π，即经过半个周期后，回路中磁通达到最大值φ=2φm+φr，当该值超过饱和磁通φs时，磁路饱和，即出现励磁涌流，如图2 所示。

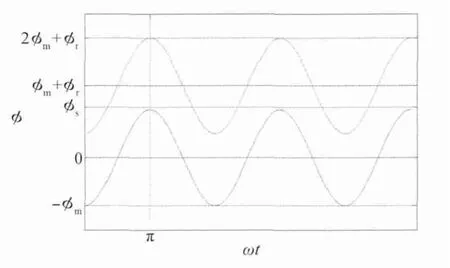
图2 励磁涌流原理Fig.2 Principle of magnetizing inrush current

励磁涌流仅见于图2 中y =φs以上的部分，涌流的间断角度为2θ0。从公式可以看出，剩磁和合闸角度共同决定了励磁涌流的峰值。当合闸角度为0 时，θ0可取得最小值为，此时饱和最为严重。

根据以上推导，可知单相变压器励磁涌流特点:(1)波形偏时间轴的一侧，呈尖顶波形;(2)涌流的大小受合闸角度的影响，合闸角为90°时，励磁涌流最小;(3)是否出现励磁涌流与剩磁有关，若φm与φr之和未超过饱和磁通φs，则无励磁涌流现象;(4)励磁涌流有间断角，间断角范围内磁通不饱和，间断角越小，饱和越严重;(5)根据实际存在的磁阻和合闸电阻，励磁涌流含有非周期分量，波形是衰减的。

2 励磁电流影响因素分析

2.1 电磁暂态模型的建立

2.1.1 ±1 100 kV 特高压直流主回路参数

±1 100 kV 特高压直流工程是目前直流最高电压等级，经过前期研究，暂推荐额定输送功率12 000 MW，受端换流站考虑直接接入500 kV 交流电网、高低端换流器分别接入500 kV 和1 000 kV 交流电网以及高低端换流器全部接入1 000 kV 交流电网(采用带500 kV 中间抽头的换流变或通过500/1 000 kV联变的方式)等3 种方式。

主回路计算得到的换流变压器主要参数见表1 ～3。

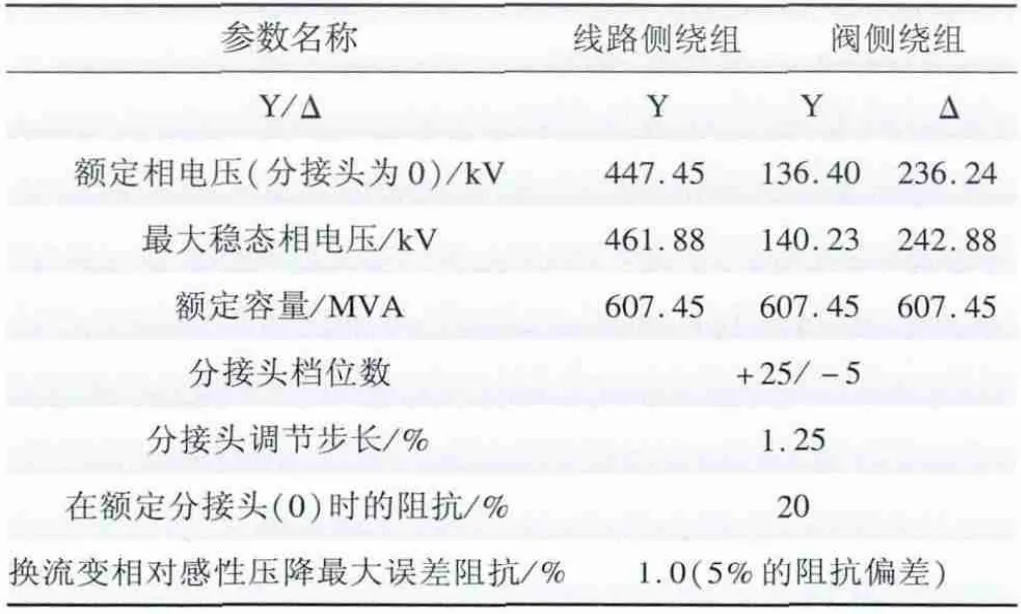
表1 送端换流变参数Tab.1 Parameters of sending-end converter transformer

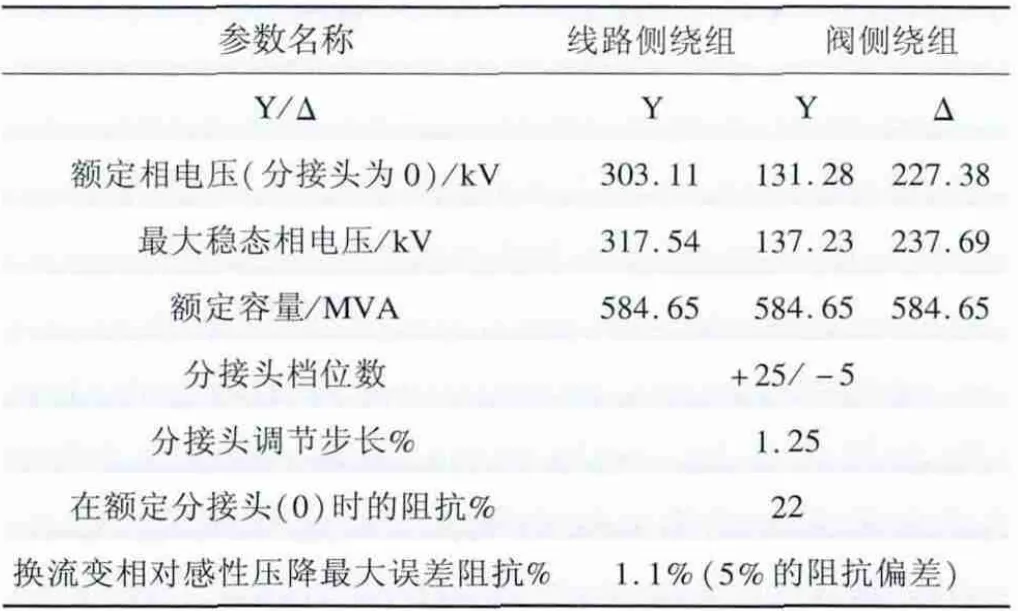
表2 受端高端换流变参数Tab.2 Parameters of receiving-end high voltage converter transformer

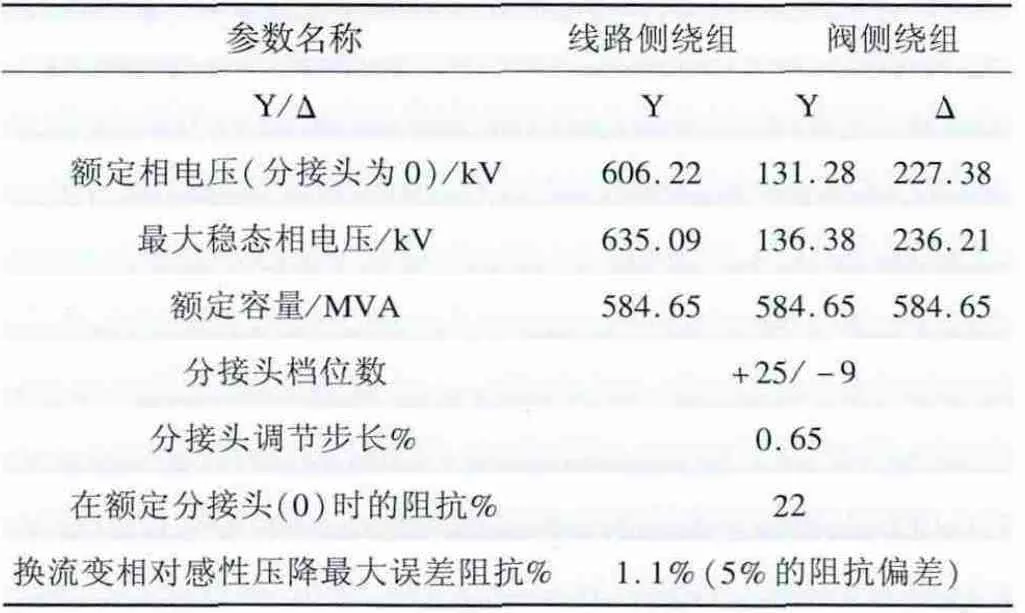
表3 受端低端换流变参数Tab.3 Parameters of receiving-end low voltage converter transformer

2.1.2 特高压换流变压器磁化特性曲线

换流变压器短路阻抗一方面能够限制直流侧短路时的故障电流，保护阀设备，另一方面过大的短路阻抗会导致无功损耗的增加。该参数与换流变压器实际设计、制造以及运输条件等有关，且在其自然阻抗附近根据实际需要优化。目前在建或在运±800 kV特高压直流换流变压器的短路阻抗为16.7% ～20%，根据目前研究，±1 100 kV 特高压直流换流变压器短路阻抗可能达到并超过22%。

为了补偿换流变压器交流网侧电压的变化，将触发角运行在适当的范围内以保证运行的安全性和经济性，要求有载调压分解开关具有一定的调压范围。

换流变压器的励磁特性曲线在电压超过额定电压后，呈现明显的饱和特性。励磁特性曲线与铁心材料、尺寸等条件有关。通常，由于工程系统参数、设计理念、技术路线、制造供货商、换流站位置、高低压端、联接方式的不同，换流变压器的励磁特性曲线存在差异。

工程中通常采用U －I 特性曲线表征变压器饱和特性，根据±800 kV 特高压换流变压器实验测量结果描绘U －I 特性曲线如图3 所示，图中依次标注了两端换流站高压端Yy 换流变压器、高压端Yd 换流变压器、低压端Yy 换流变压器、低压端Yd 换流变压器饱和特性。

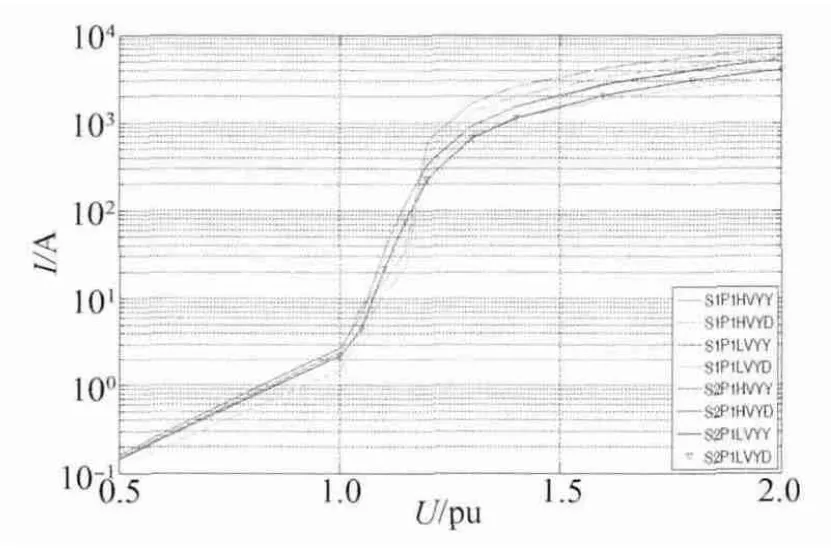
图3 ±800 kV 特高压直流换流变压器典型磁化特性曲线Fig.3 Typical magnetization characteristic curves of±800kV UHVDC converter transformer

由图3 可知，当换流变压器电压高于额定电压后，出现明显的饱和，励磁涌流显著增加。换流变按照图中顺序，U －I 曲线依次下降，即按照现有设计，特高压直流高压端的换流变压器在空载合闸时，更容易产生较大的励磁涌流。

根据调研，换流变压器励磁特性曲线只与铁心大小和所选磁密有关，因此，分层接入方式对换流变压器及其励磁特性曲线的影响很小，只与换流变压器所用铁心大小和所选磁密有关。

根据换流变压器制造厂家提供的资料，±1 100 kV高压端换流变压器按照型号ZZDFPZ-541500/750 －1100，阻抗22%，阀Y 侧测量，保守估计，空载损耗约365 kW，低压端按照型号ZZDFPZ-541500/750 －550，阻抗22%，阀Y 侧测量，保守估计，空载损耗约210 kW，其他数据可根据锦屏项目所提供曲线进行拟合。由于实际情况根据所用硅钢片型号会有较大变化，以上数据偏差会较大，大过容量的影响，因此，传输容量11 000 MW和12 000 MW 可以使用同一曲线。

2.1.3 电磁暂态模型的建立

本文所采用变压器模型为特高压直流换流变压器。换流变压器是联接交流系统与换流阀的电力变压器，能够为换流阀提供一个中性点不接地的三相换相电压。换流变压器与换流阀是构成换流单元的主体。换流变压器参数需要考虑短路阻抗、有载调压开关设置以及饱和特性的影响。

建立用于特高压直流换流变压器励磁涌流用的电磁暂态模型。其中，变压器饱和曲线根据实际换流变压器U －I 特性表征。模型中，为考虑空载合闸影响，换流变压器阀侧可认为是开路状态，需要建立符合实际工程设计水平年的交流系统模型、换流变压器模型(含饱和特性)、合闸电阻模型以及其他的开关模型等。

2.2 系统短路容量

在换流变空载合闸和故障后恢复过程中，系统短路容量将对稳定换流母线电压影响显著。利用电磁暂态仿真模型进行仿真研究，分别选择典型工程交流系统设计水平年的最大短路电流63 kA 和最小短路电流11.7 kA 建立等效模型模拟换流变压器空载合闸操作，其他仿真条件相同，换流变压器交流侧电流波形见图4。

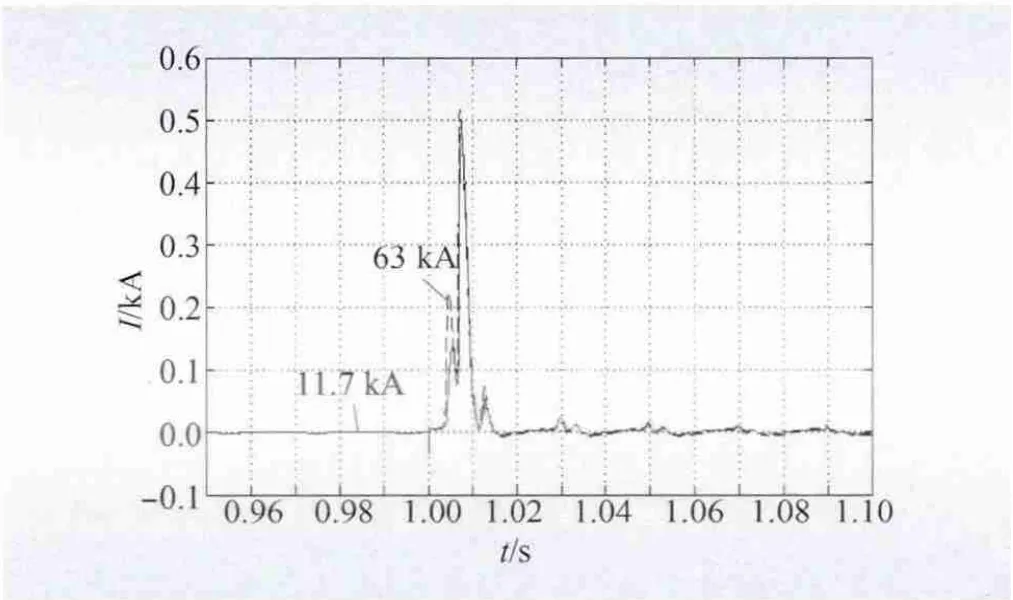
图4 系统阻抗因素的影响Fig.4 Influence of system＇s impedance

由图4 可知，系统短路容量较大时，换流变压器励磁涌流相应较大。系统短路容量对应于系统等值阻抗，系统短路电流越大，相应的系统阻抗越小，反之短路电流越小，则相应的系统阻抗越大;在充电回路中，相应的较高阻抗对励磁涌流会起到限制作用，因此，系统短路容量大时，励磁涌流较大。本文所研究对象系统在最大短路容量时的励磁涌流较最小短路容量时高7%。

2.3 合闸电阻

为分析合闸电阻影响，假设不考虑单相换流变压器漏抗，交流系统短路容量无穷大，设置合闸电阻，含合闸电阻的等效电路见图5。

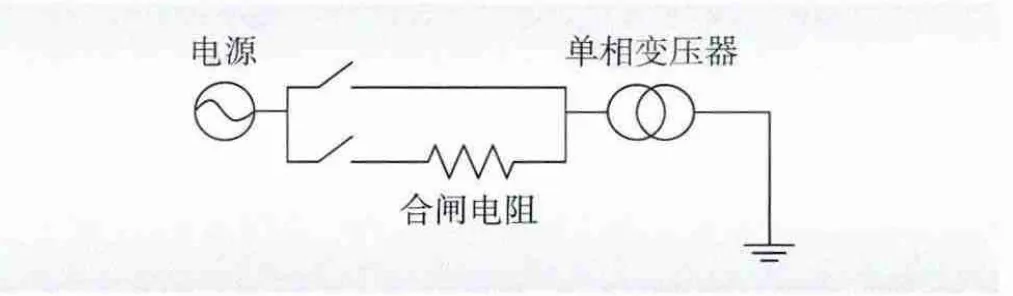
图5 有合闸电阻的等效电路Fig.5 Equivalent circuit with closing resistor

电源合闸时电源电势为Umsin(ωt +α)，则回路电压方程为

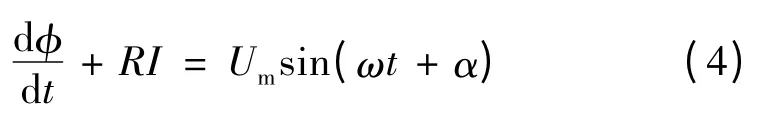
式中:R 为断路器合闸电阻;I 为合闸电流。为简化说明，通常可把变压器的基本磁化曲线作折线处理，如图1 所示，设φ ＞φs时的电感为L，则设变压器磁路饱和后，其静态电感为L =(φ－φs)/I，代入式(4)可得:

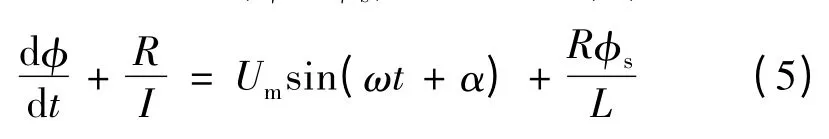
将式(5)看作一个以φ 为未知函数的常系数线性微分方程，设在接通电源之前，铁心内有剩磁φr存在，则一般解为

励磁涌流为

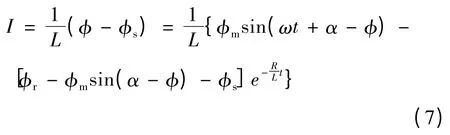
由式(7)可知，合闸电阻除了具有降低励磁涌流的峰值外，还具有加速衰减的效果。

图6 为±800 kV 换流变合闸电阻对抑制励磁涌流的影响效果。分别对无合闸电阻，800 Ω 合闸电阻以及1 600 Ω 合闸电阻的效果进行了比较，其他仿真条件相同。由仿真结果可知，800 Ω 合闸电阻和1 600 Ω合闸电阻下励磁涌流的峰值分别仅为无合闸电阻时的7.0%和3.7%。因此，合闸电阻的存在对抑制励磁涌流具有显著效果，随着合闸电阻进一步增加，抑制效果会较之前降低。

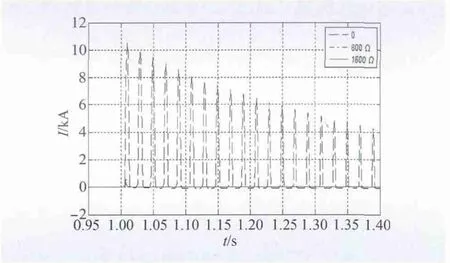
图6 合闸电阻的影响Fig.6 Influence of closing resistor

2.4 选相合闸

合闸相位角对励磁涌流有显著影响，式(7)中，可简化设合闸电阻为0，则

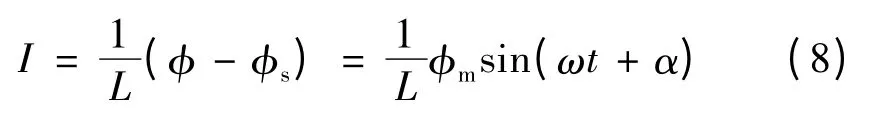
实际上，过零点合闸时，励磁涌流最小，而当合闸相位与过零点相差90°时，则涌流最大。图7 为不同合闸相位角时的交流侧电流。由图7 可见，其他仿真条件相同时，与系统相位角相差90°时，励磁涌流最大。

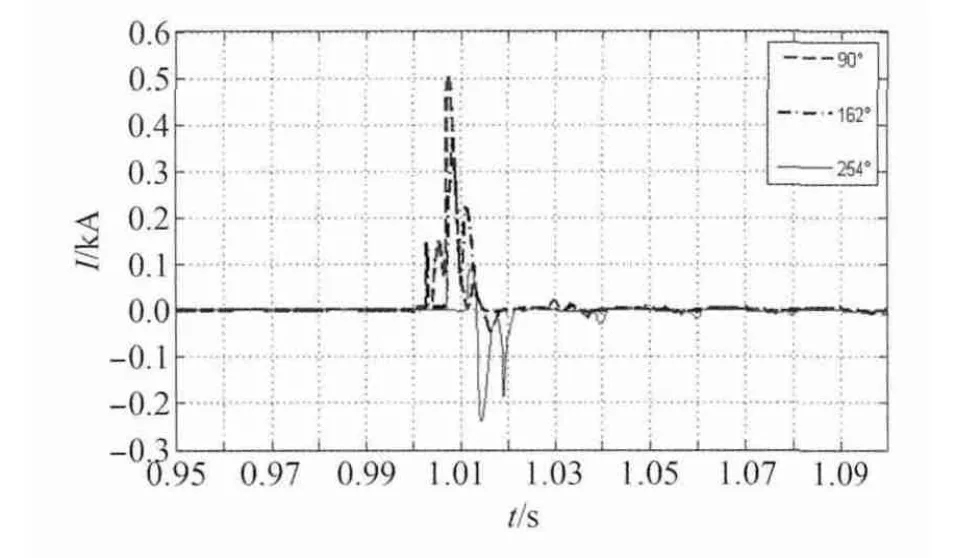
图7 合闸相位的影响Fig.7 Influence of closing phase

本文所做研究均基于变压器铁心无剩磁的条件，若存在剩磁，则当剩磁的大小和方向与系统电压将要产生的磁通相同时，可以避免合闸时铁心饱和。

3 结 论

(1)不考虑剩磁影响条件下，高压端换流变压器励磁涌流最高。

(2)系统短路容量在模型中的直接反映是等值交流系统的阻抗大小，系统短路容量大时，励磁涌流较大，反之亦然。

(3)合闸电阻对励磁涌流具有明显抑制作用，但随着电阻值的增加，抑制效果会逐步降低。

(4)过零点合闸时，励磁涌流最小，而当合闸相位与过零点相差90°时，则涌流最大。

［1］浙江大学发电教研组直流输电科研组．直流输电［M］．北京:水利电力出版社，1985:23-25．

［2］刘振亚．特高压交直流电网［M］． 北京:水利电力出版社，2013:22，101-103．

［3］舒印彪，刘泽洪，高理迎，等． ±800 kV 6 400 MW 特高压直流输电工程设计［J］．电网技术，2006，30(1):1-8．

［4］常勇． 500 kV高岭换流站换流变空载充电励磁涌流分析［J］． 电网技术，2009，33(1):97-100．

［5］周长春，徐政．联于弱交流系统的HVDC 故障恢复特性仿真分析［J］．电网技术，2003，27(11):18-21．

［6］Saied M M． A study on the inrush current phenomena in transformer substations ［C］//Proceedings of IEEE Industry Applications Conference Thirty-sixth IAS Annual Meeting，Chicago:IEEE，2001(2):1180-1187．

［7］Bronzeado H，Yacamini R． Phenomenon of sympathetic interaction between transformers caused by inrush transients［J］． IEEE Proceedings，Science，Measurement and Technology，1995，142(4):323-329．

［8］Bronzeado H，Brogan P，Yacamini R，Harmonic analysis of transient currents during sympathetic interaction［J］． IEEE Transactions on Power Systems，1996，11(4):2051-2054．

［9］翁汉琍，林湘宁．换流变压器差动保护异常动作行为分析及对策［J］．中国电机工程学报，2009，29(31):87-94．

［10］陈曾田．电力变压器保护［M］． 北京:中国电力出版社，1998:56-59．

［11］何奔腾，徐习东．波形比较法变压器差动保护原理［J］． 中国电机工程学报，1998，18(6):395-398．

［12］胡玉峰，陈德树．基于采样值差动的励磁涌流鉴别方法［J］． 中国电机工程学报，2000，20(9):55-58．

［13］Guzman A，Zocholl S，Benmouyal G，et al．A current-based solution for transformer differential protection，part II:description and evaluation［J］．IEEE Transactions on Power Delivery，2002，17(4):886-893．

［14］王增平，徐岩，王雪，等．基于变压器模型的新型变压器保护原理的研究［J］．中国电机工程学报，2003，23(12):54-58．

［15］田庆．12 脉动换流变压器对称性涌流现象分析［J］． 电力系统保护与控制，2011，39(33):133-137．