插值法在《财务管理》教学中的应用

高小雪

插值法在《财务管理》教学中的应用

高小雪

在《财务管理》货币时间价值的计算中，常常用到插值法，但几乎所有的教材都没有对插值法的原理进行清楚的解析，对于初学者来说比较难以理解。本文根据教学实践经验，利用图示法和案例解释插值法的数学原理，更容易理解和掌握。同时，分析了插值法的使用范围。

货币时间价值；插值法；图示法

在《财务管理》时间价值计算中，经常会遇到已知终值或现值，求计息期或利率的问题，然而系数表的使用范围有限，教学中通常引入插值法解决问题。插值法又称“内插法”，是函数逼近的一种重要方法，是利用函数f (x)在某区间中插入若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f(x)的近似值，这种方法称为插值法。

一、插值法的几何原理

插值法利用了几何上相似三角形对应边长成比例的原理，将数学应用于解决实际问题。插值法最早在1976年提出用于解决车辆线路问题。《财务管理》中使用的插值法是简单的线性插值法。下面用图形（图1）说明简单线性插值法的几何意义。图1是某线性函数f（x），求X2。根据相似三角形对应边长成比例的几何原理，△CBD∽△CAE可知，因X1、X3、f(X1)、f(X2)、f(X3)已知，对等式进行恒等变换可求得未知数X2。这就是插值法的基本原理。

图1

在图1中，f（x）为线性函数，在图中体现为一条直线。但是，在《财务管理》的时间价值计算中，f（x）为非线性函数，在坐标图中亦非直线，而是一条曲线。因此，根据上述原理使用插值法求得的结果并非真实结果，而是存在一定误差。在图2中，我们可以清晰的看到真实结果与插值法求得的结果之间的误差。

图2

二、插值法的图示解析

在《财务管理》时间价值的计算中使用插值法，如果只是以函数式来求解，对学生而言有些抽象，也不容易理解，但如果以图示法，学生会比较直观而轻松地化解疑问。下面用两个具体案例来对插值法进行图示解析。

案例一：计划现在起每年年末存进银行1000元、假设利率为10%，那么几年之后可以从银行取出5000元？

解析：（F/A，10%，n）=5000/1000=5，在年金终值系数表中无法查到系数为5的期数n，要找到临界值构造相似三角形计算。当期数为4时，系数是4.6410；当期数为5时，系数是6.1051。因此，期数应当介于4和5之间。插值法求解如图3所示。

函数（F/A，10%，n）为增函数，可以近似的把两个临界值之间的曲线ABC近似的看成直线，构造图1所示的相似三角形。根据插值法相似三角形对应边长成比例的几何原理可知：

图3

案例二：假设现在存进银行5000元，在未来8年每年年末都能从银行取出1000元，那么银行利率应为多少？

解析：（P/A，i，8）=5000/1000=5，在年金现值系数表中无法查到系数为5的利率i，要找到临界值构造相似三角形计算。当利率为11%时，系数是5.1461；当利率为12%时，系数是4.9676。因此，利率应当介于11%和12%之间。插值法求解如图4所示。

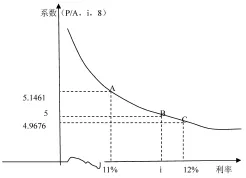
图4

函数（P/A，i，8）为减函数，可以近似的把两个临界值之间的曲线ABC近似的看成直线，构造图1所示的相似三角形。根据插值法相似三角形对应边长成比例的数学原理可知：

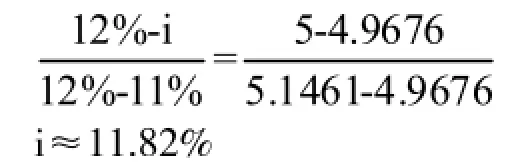
通过图示法，我们可以直观且较容易的理解插值法的具体应用。当我们很熟悉插值法之后，可以不必画出坐标图就可以进行插值法的求解。

例三：某项目投资方案，当折现率为12%时，方案的净现值为250万元，当折现率为14%时，其净现值为-50万元，那么该投资方案的内含报酬率是多少？

解析：能够使净现值NPV=0的折现率就是项目的内含报酬率。

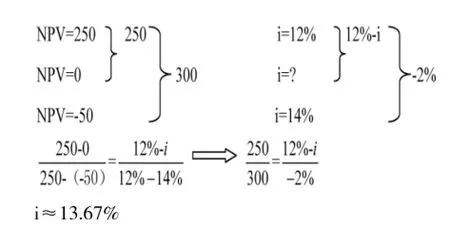
三、插值法的使用范围

在《财务管理》货币时间价值的计算中，有些其实是可以通过计算器得到一个精确结果。对于求解年金终值系数、年金现值系数中的利率i或者期数n的问题，在求解的公式中利率i或者期数n不只出现一次或不容易通过恒等变化得到一个不含未知量的等式，通过计算器也往往得不到精确结果。在很多的《财务管理》教材中，凡是遇到货币时间价值无法查系数表计算的问题，都一概使用“插值法”解决。其实，在教学实践中应区别对待。对于求解年金终值系数、年金现值系数中的利率i或者期数n的问题，可以使用插值法。但是对于求解复利终值系数、复利现值系数中利率i或期数n的问题完全可以用公式算术式准确的计算结果，如果使用了插值法，反而麻烦而且得到的只是一个近似的结果。现举例说明。

案例四：已知终值F=3000，现值P=1000，期数n=10，求利率i。

先使用插值法计算，查表可知两个临界值分别是（F/P，11%，10）=2.8394（F/P，12%，10）=3.1058，由插值法可得算式，则利率i≈11.60%。

再使用公式算数法计算，F=3000=1000(1+i)，恒等变换之后

四、结论

在《财务管理》货币时间价值的计算中，使用“插值法”可以解决系数表局限性的问题。同时，在教学实践中，使用图示法可以帮助学生直观且更好的理解插值法的原理。但是，对于插值法的使用，应针对不同问题区别对待，不能一概而论，对于求解复利终值系数、复利现值系数中利率i或期数n的问题出于准确性的考虑就不适合采用插值法。

[1]关继芳.插补法简解[J].会计之友,2008（6）.

[2]田笑丰.财务管理教学中插值法的快速理解和掌握[J].会计之友,2008（4）:74～75.

[3]郭复初，王庆成.财务管理学[M].北京:高等教育出版社，2005，8:57.

（作者单位：黄河科技学院）