顾及RPDOP值的GPS变形监测抗差Kalman滤波*

张 超 戴吾蛟 曾凡河 潘家宝

1)中南大学地球科学与信息物理学院，长沙 410083

2)湖南省精密工程测量与形变灾害监测重点实验室，长沙410083

1 引言

由于Kalman 滤波不需要存储过去的观测数据，可以大大减少时空复杂度，便于实时数据处理，因而在动态变形监测、GPS 动态定位等领域中得到了广泛的应用［1－3］。但Kalman 滤波的效果与准确的状态噪声与观测噪声密切相关，当观测值中含有粗差时，标准Kalman 滤波的估值不准确，甚至导致滤波发散。为了抵抗观测值中粗差的影响，杨元喜等［4－6］基于抗差估计理论提出了抗差Kalman 滤波，余学祥等［7］也从预测残差和多余观测分量构造等价增益矩阵出发提出了抗差Kalman 滤波模型(RKF，Robust KF)。这些抗差Kalman 滤波模型的实质都是根据观测值残差进行粗差探测并对含有粗差的观测值进一步降权或剔除该观测值，以抵抗粗差的影响，但降权将直接影响抗差的效果。在GPS变形监测中，常利用Kalman 滤波对GPS 解算后得到的位移观测值进行动态滤波，但受观测环境的影响，位移观测值中常含有粗差，其中卫星图形结构并不是一个定位误差源，通常会导致定位解算时法方程不稳定［7］，降低定位的精度。而卫星定位几何精度因子(PDOP，Position Dilution of Precision)(相对定位时为RPDOP)［8］反映出卫星图形结构越好，PDOP 值越小，定位解算精度也越高［9］。所以为了提高抗差效果，本文针对GPS 变形监测中一般采用相对定位的特点，通过引入GPS 相对定位中的几何精度因子(RPDOP，Relative Position Dilution of Precision)值作为先验信息来探测并定位观测值中的粗差，从而对其进行降权处理，以达到更佳的抗差效果。

2 抗差Kalman 滤波模型

标准Kalman 滤波要求动态噪声和观测噪声是高斯白噪声序列，但在实际应用中难以满足该条件［10］。当有粗差存在于观测值向量L 中时，由Kalman 滤波的递推方程可知，状态预测向量1)及误差都将受到来自粗差的影响。通过分析M 估计等价权原理，增益矩阵Kk能够反映粗差的影响，所以可以将观测噪声协方差阵用合适的权函数代替，这样粗差对估计结果的影响就可以得到一定程度的削弱甚至消除。

杨元喜基于稳健估计思想，构造观测向量抗差等价权矩阵［11］。权函数采用IGGⅢ方案［12］，表示为:

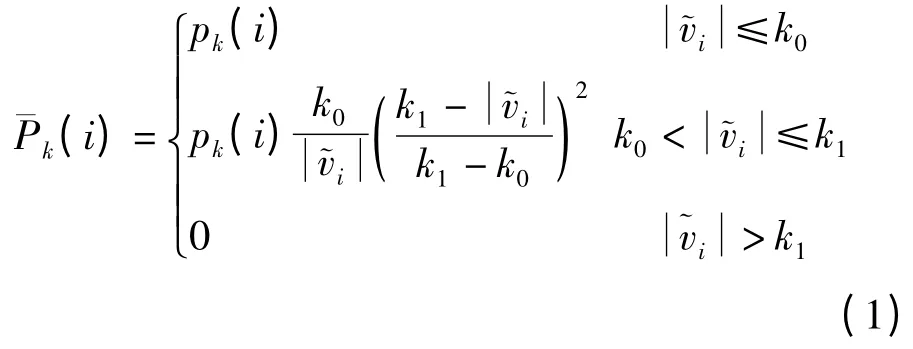
在变形监测中，一般情况下监测点的观测值都是测点的三维坐标，这时再根据观测向量的标准化残差来计算显然不太合适。根据Kalman 滤波中的预测残差向量特征，改进如下［13］:

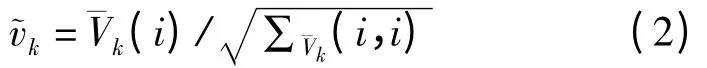
3 顾及RPDOP 值的GPS 变形监测抗差Kalman 滤波模型

由于在GPS 变形监测中，要求获得较高精度的形变量，多采用相对定位模式［14］。由于RPDOP 值实质上反映的是相对定位中法方程结构的稳定性(病态性)。所以本文引入RPDOP 值作为先验信息，提出顾及RPDOP 值的GPS 变形监测抗差Kalman 滤波模型。该模型首先要计算出RPDOP 值，RPDOP 推算过程如下［15］:

在观测时刻t，在两个测站1 和2 上对卫星p 和q 进行同步观测，测站1 为基线的已知端，其坐标已知，可构成载波相位的双差观测方程［16］，为便于书写，省略双差符号:

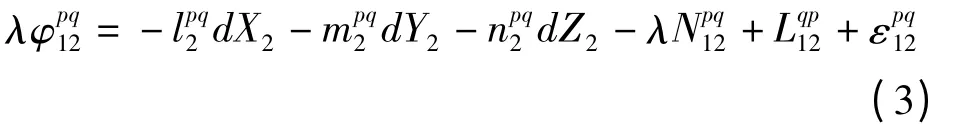
假设两测站的同步观测卫星个数为n，则相应地可以获得(n－1)个双差观测值，其误差方程为:

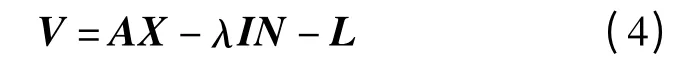
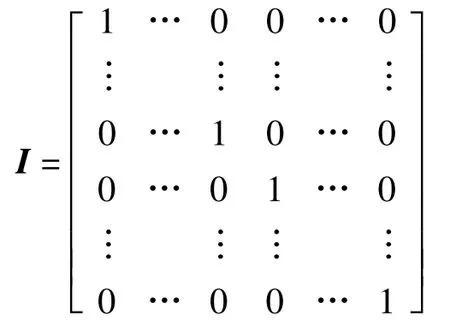
式中未知参数的协因数阵为:

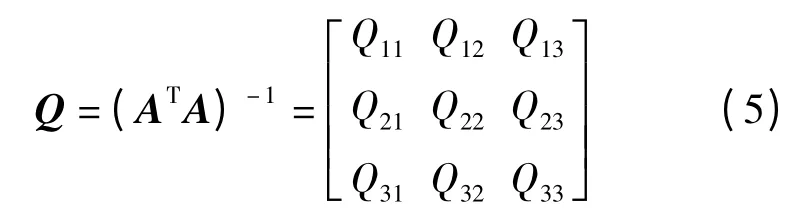
经过推导，可以获知t 时刻，相对定位空间位置精度因子为:

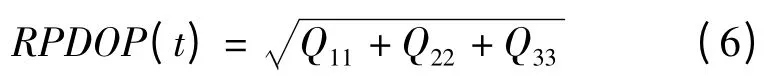
由于相对定位在GPS 变形监测中已经得到广泛使用，所以只需在原有观测资料的基础上，求取RPDOP 值即可。由于顾及RPDOP 值的抗差Kalman滤波具体的算法实现与一般的抗差Kalman 滤波相比在实现的过程中多了一步RPDOP 值的判断，若RPDOP 值大于阈值就对其进行降权处理，此处阈值的设定具有一定的经验性，本文通过实验调试，将其设定为4.0，当大于此阈值时，将其权降低1 000 倍，否则就直接执行一般的抗差Kalman 滤波。

4 实测数据处理

实测数据来自湖南省郴宁高速公路一边坡点2012-01—12月的变形监测数据。数据通信用GPRS 无线传输，每个历元的观测结果是3 个小时的静态解。由于此边坡地处山区，信号质量较差，存在严重的信号遮挡，同时还受周跳、信号中断的影响，一些时段的数据存在不同程度的缺失。此外，受多路径效应和信号衍射误差的影响，监测结果频繁出现粗差(图1)。从图中可以明显看出位移序列数据存在明显奇异值，这些奇异值实际都为粗差。本次试验中，系统状态模型为随机游走模型，采用标准Kalman 滤波、IGGIII 抗差Kalman 滤波以及RPDOP 抗差Kalman 滤波三种方法对实际边坡GPS 变形监测数据进行处理与比较分析，其中抗差因子的阈值设定k0=2.5，k1=4.5，而RPDOP 值的阈值则设为4.0。图1～3 分别为三种滤波方法的结果与原始数据序列的对比图，从图中可以看出，本文提出的改进算法抗差效果最佳。为了进一步定量评价滤波的效果，本文还采用小波滤波方法对原始观测值序列进行滤波，鉴于小波滤波具有很强的去奇异值及滤波去噪能力，本次实验以小波滤波的结果作为参考，计算三种方法滤波后的残差RMS 值，具体结果见表1。

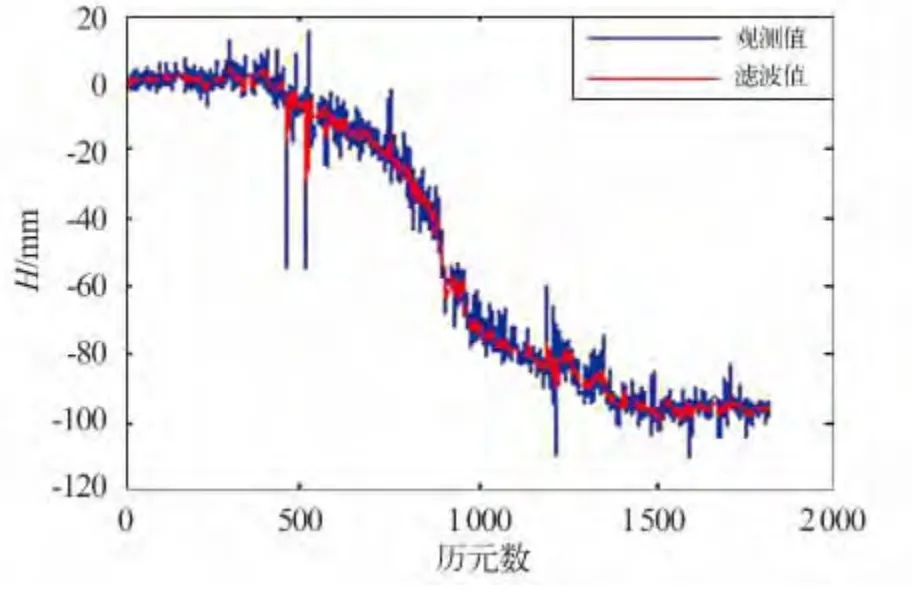
图1 标准Kalman 滤波Fig.1 Standand Kalman Filter

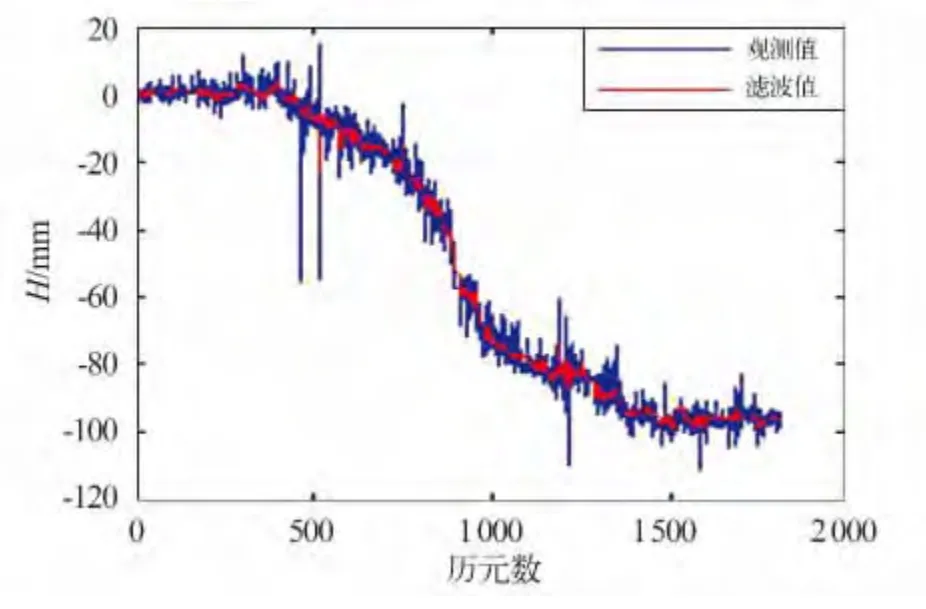
图2 抗差Kalman 滤波Fig.2 Robust Kalman Filter

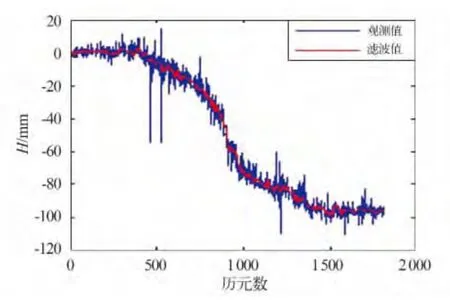
图3 顾及RPDOP 值的抗差Kalman 滤波Fig.3 RPDOP based Robust Kalman Filter

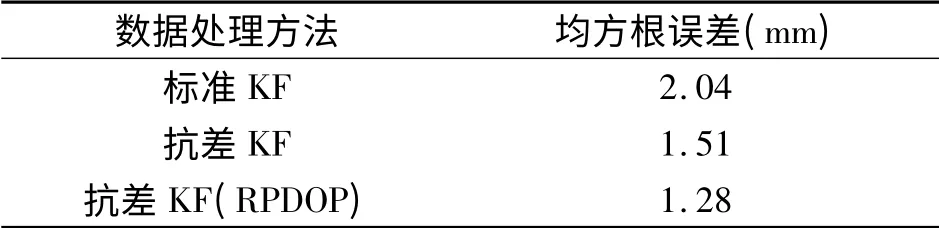
表1 三种卡尔曼滤波方法的RMS 统计值Tab.1 RMS values with 3 methods

由表1 可知，顾及RPDOP 值的抗差Kalman 滤波处理数据的精度最高，IGGIII 抗差Kalman 滤波模型其次，标准Kalman 滤波模型精度最低。

为了进一步分析顾及RPDOP 值的抗差Kalman滤波的抗差效果，对明显含有粗差的第522 历元位移数据进行分析。第522 历元位移大小是－54.9 mm，平均RPDOP 值为9.72。而一般正常值RPDOP 在4.0 以下，观察其前后的数据也可以看出，此观测数据明显偏离正常的变形位移范围，是个较大的粗差。若采用标准Kalman 滤波处理，其权值为865，滤波后值为－29.5mm，与小波滤波参考值相差－18.3 mm;采用IGGIII 抗差后，其等价权为476，滤波后值为－24.4 mm，与小波滤波参考值相差－13.1 mm;而考虑RPDOP 值后，权降低至0.476，滤波后值为－10.2 mm，与小波滤波参考值相差1.0 mm。这说明仅利用标准化残差进行抗差处理是不够的，而RPDOP 值本身可作为GPS 相对定位精度的一个指标，以此作为先验信息进行抗差降权处理是合理的，因此顾及RPDOP 值的抗差Kalman 滤波效果最佳。

5 结语

在GPS 变形监测中，通常对解算后得到的位移值进行动态滤波，采用抗差Kalman 滤波时，通常根据标准化的残差进行粗差探测和降权处理，但本文研究发现标准化残差不能完全反映GPS 位移观测值的质量，而综合考虑GPS 相对定位几何精度因子RPDOP 值可更准确地评价GPS 位移观测值的质量，因此本文引入RPDOP 值作为先验信息，对GPS 位移观测值中的粗差进行探测并作进一步降权处理，可起到更强的抗差作用。实际GPS 滑坡变形监测数据应用结果表明该方法较一般的抗差Kalman 滤波抗差效果更佳。同时，也说明先验信息的利用有助于提高抗差Kalman 滤波的效果和可靠性。

1 Jang C W，Juang J C and Kung F C.Adaptive fault detection in real-time GPS positioning［J］.IEE Proceedings-Radar，Sonar and Navigation，2000，147(5):254－258.

2 付梦印.Kalman 滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003.(Fu Mengyin.Kalman filtering theory and its application to navigation system［M］.Beijing:Science Press，2003)

3 万德钧，等.GPS 动态滤波的理论，方法及其应用［M］.南京:江苏科学技术出版社，2000.(Wan Dejun，et al.GPS dynamic filtering theory，method and its application［M］.Nanjing:Jiangsu Science and Technology Press，2000)

4 杨元喜，张双成.导航解算中的系统误差及其方差协方差矩阵拟合［J］.测绘学报，2004，33(3):189－194.(Yang Yuanxi and Zhang Shuangcheng.Fittings of systematic errors and covariance matrices in navigation［J］.Acta Geodetica et Cartographica Sinica，2004，33(3):189－194)

5 杨元喜.动态系统的抗差Kalman 滤波［J］.解放军测绘学院学报，1997，14(2):79－84.(Yang Yuanxi.Robust Kalman filter for dynamic systems［J］.Journal of the PLA Institute of Surveying and Mapping 1997，14(2):79－84)

6 Yang Y，He H and Xu G.Adaptively robust filtering for kinematic geodetic positioning［J］.Journal of Geodesy，2001，75(2):109－116.

7 冯尊德，卢秀山，郭英.GPS 定位中几何精度因子的病态性诊断及其递推计算［J］.煤炭学报，2006，31(5):591－584.(Feng Zhunde，Lu Xiushan and Guo Ying.Diagnostics of pathological condition of geometric factor of precision and its substitution calculation in GPS［J］.Journal of China Coal Society，2006，31(5):591－584)

8 Nielsen R O.Relationship between dilution of precision for point positioning and for relative positioning with GPS［J］.IEEE Trans Aerospace and Electronics Systems，1997，33(1):333－338.

9 Masahiko Kihara.Study of a GPS satellite selection policy to improve positioning accuracy［J］.IEEE Position Location and Navigation Symposium，1994，267－273.

10 余学祥，吕伟才.抗差卡尔曼滤波模型及其在GPS 监测网中的应用［J］.测绘学报，2001，30(1):28－31.(Yu Xuexiang and Lü Weicai.Robust Kalman filtering model and its application to GPS monitoring networks［J］.Acta Geodetica et Cartographica Sinica，2001，30(1):28－31)

11 Koch K R and Yang Y.Robust Kalman filter for rank deficient observation models［J］.Journal of Geodesy，1998，72(8):436－441.

12 杨元喜.抗差估计理论及其应用［M］.北京:八一出版社，1993.(Yang Yuanxi.Robust estimation theory and its application［M］.Beijing:Bayi Press，1993)

13 伍锡锈.动态变形监测中的Kalman 滤波方法研究［D］.中南大学，2011.(Wu Xixiu.Study on Kalman filtering for dynamic deformation monitoring［D］.Central South University，2011)

14 胡友健，等.论GPS 变形监测技术的现状与发展趋势［J］.测绘科学，2006，31(5):155－157.(Hu Youjian，et al.On the status quo and development trend of GPS technology in deformation monitoring［J］.Science of Surveying and Mapping，2006，31(5):155－157)

15 刘超，等.GPS/伪卫星相对定位中伪卫星优化布设模型研究［J］.中国矿业大学学报，2012，41(1):120－126.(Liu Chao，et al.An optimal pseudolites location model of GPS/pseudolites integrated relative positioning［J］.Journal of China University of Mining＆Technology，2012，41(1):120－126)

16 李征航，黄劲松.GPS 测量与数据处理［M］.武汉:武汉大学出版社，2005.(Li Zhenghang and Huang Jinsong.GPS surveying and data processing［M］.Wuhan:Wuhan University Press，2005)