模拟地层条件下膏泥岩高频声波测试及频散外推对比研究

李双贵，张 俊，易 浩，周 文，单钰铭，尹 帅

（1.西南石油大学石油工程学院，成都610500；2.中国石化西北油田分公司工程技术研究院，乌鲁木齐830011；3.成都理工大学能源学院，成都610059）

模拟地层条件下膏泥岩高频声波测试及频散外推对比研究

李双贵1，2，张 俊2，易 浩2，周 文3，单钰铭3，尹 帅3

（1.西南石油大学石油工程学院，成都610500；2.中国石化西北油田分公司工程技术研究院，乌鲁木齐830011；3.成都理工大学能源学院，成都610059）

为了获得塔里木A区古近系地层中膏泥岩在声波测井20 kHz频率下纵横波时差之间及与其他静力学参数之间的转换关系，开展了室内1 000 kHz高频声波测试。根据测试声波波速值、品质因子和频散方程外推20 kHz频率的声波波速。2种频率下波速或声波时差对比分析表明：模拟地层条件下转换后的纵波时差（实验校正）与测井纵波时差更为接近；常温到85℃范围内相同净围压下波速和品质因子变化较小，波速变化可以忽略，品质因子变化范围为5%～7%；在不断增加净围压条件下，波速和品质因子都增加，且幅度显著；模拟地层条件下与常温、常压下相比，纵波波速增量为2.7%～8.4%，纵波品质因子增量为27%～58%，膏泥岩频散度为7.4%～24.4%，平均为15.12%，频散度较大。通过对频散方程变形得出了一种可直观表现本区膏泥岩在模拟地层条件下品质因子与波速降低幅度之间的表达式，同时根据膏泥岩品质因子影响因素，将该区古近系地层的膏泥岩纵波按由高到低划分为Ⅰ，Ⅱ，Ⅲ共3个频散等级，最后探讨了频散效应在横波时差预测中的应用。结果表明：在1 000 kHz和20 kHz频率下，利用纵波时差预测的横波时差在该区膏泥岩声波时差变化范围内，平均相对误差仅2%，误差整体随着石膏含量的增加而增大，这2种频率下纵横波时差拟合公式都可应用到横波时差预测（利用测井纵波时差值进行预测）中，但由于膏泥岩频散度大，因而2种频率间声波时差值变化较大，应用时应进行频散校正。

地层条件；膏泥岩；声波；波速频散；纵横波时差；品质因子

0 引言

全世界以膏盐岩为盖层的油气评价单元数占总评价数的8%，但却控制了近55%的油气储量（USGS，2006）［1］。国内各含油气盆地均有膏盐岩层覆盖［1-2］，其中盐下储层已成为未来勘探的重点领域。塔里木盆地纯膏岩、纯盐岩或膏盐泥互层的区域性盖层主要分布在寒武系（最厚400m）和中上石炭系（最厚150m）地层中［1］。笔者主要研究的是塔里木盆地古近系地层膏（文中均指硬石膏）泥岩，其基本特征如下：①GR低（10～65API）；②密度大，当硬石膏质量分数＞90%时，密度＞2.9 g/cm3；③声波时差较盐岩和泥岩高，主要分布在50～100μs/ft（1 ft=0.3048m）；④电阻率值高（0.1Ω·m≤RLLD≤10 000Ω·m）。膏盐岩作为良好盖层的同时也会带来一些问题，自1901年人们就发现膏盐岩层由于压力梯度与上下层之间差异较大［3］而易造成井壁失稳、套管变形及泥浆密度难确定等工程问题，同时由于膏盐岩往往分布范围较广，所以人们不可能避开它而进行钻探，这就需要对其力学参数的性质进行分析。研究内容一般包括矿物成分鉴定、实验测试和测井解释，最终建立连续力学参数测井解释剖面并进行地应力分析或应力场模拟。声波频散是指室内高频测试的波速值与其他频率（测井、地震）测试的波速值不相等，声波在介质中传播会发生衰减和频散，岩石波速从高频（＞100 kHz）到低频（＜0.1 kHz）均可发生频散［4］。而常规实验仅能测试频率＞100 kHz波速，因此，不同频率间波速可以根据频散方程进行转换，高频转换成低频时波速会降低，室内分析测试的结果未必能直接应用到油田测井中。实验分析的最终目的是为了根据油田测井资料对未知力学参数进行计算或预测，波速的差异最终会反映到各力学参数值及地应力的大小上。鉴于膏泥岩作为非储层，目前国内未有其频散研究的报道，笔者试用频散方程对该类型岩石的波速频散效应进行分析，以期为膏泥岩力学参数的合理评价、正确认识地层、制定合理套管强度标准、进行地应力评价及确定合理的泥浆密度等方面的研究提供一定的借鉴作用。

1 实验样品及原理

实验样品取自塔里木盆地A区古近系地层，深度为3 653～3 658m，样品共分8组（图1中图例所示），主要成分为泥质和硬石膏，2种组分质量分数之和平均90%，泥质质量分数为35%～70%，平均52%，硬石膏质量分数为10%～90%，平均约44%，2种组分此消彼长，此外还含有少量白云石、石英粉砂及微量炭屑、氧化铁和黄铁矿等，偶见重矿物锆石。利用“MTS岩石物理测试系统”对样品进行不同围压和孔压下的声波测试。仪器上限条件：围压为140MPa，孔压为70MPa，温度为200℃，压力传感器误差＜1%，声波换能器对本次实验25mm直径样品的频率为1 000 kHz。实验温度选取：根据测井（TEMP）结果显示取心层温度主要分布在85～87℃，因而选择85℃。实验有效围压的选取：研究区古近系地层为正常压实，压力系数近似为1，地层压力约为35MPa，而根据古近系上覆地层平均密度计算的上覆压力大约为85MPa，因而实验中设定围压为60MPa，孔压为10MPa，从而使实验中的有效围压（50MPa）接近地层的有效应力。实验中声波［纵波（vP）和横波（vS）］波速可由电脑自动获取，保留4位有效数字，岩石中横波和纵波往往具有一定联系，笔者主要探讨纵波频散效应。品质因子（Q）是声波频散分析的重要参数，实验中利用铝块为参考样，采用文献［5］中的方法（频谱比法）计算出实验岩样的衰减系数及Q值，铝样一般认为是不发生声波衰减的标准介质，在频率为51～1 250 kHz内频散度只有2.26%［6］，实验数据可靠。频散分析中的几个参数方程如式（1）、式（2）及式（3）所示。

图1 20 kHz/1MHz纵波波速对比Fig.1 Comparison of compressionalwave velocity at 20 kHz and 1MHz

值得一提的是岩石的频散机制到目前仍然没有完全被揭示，但一般认为其原因隐藏在强非均质性微观尺度上［7］。频散方程适用于黏弹性介质，岩石往往表现出黏弹性，其产生主要是由于岩石自身微观属性（颗粒孔、晶、缝之间的接触或摩擦）及孔隙流体黏滞流动及散射等［8］。散射会使超声波能量减弱，这主要由岩石微构造及微组分等的形态与声波波长之间的关系决定。砂、泥岩波速实验值与外推计算值在实验频率范围内具有较好的匹配性［6］，膏泥岩的黏弹性主要体现在：①矿物成分组合。实验中大多数样品在镜下观察（图版Ⅰ）均表现为硬石膏单晶呈针状或纤状，集合体呈毯状或脉状，在岩石中呈斑块状或分散状，具有一定纹理，顺纹理偶见一些细微裂缝，局部见硬石膏受压蚀发生变形，硬石膏形成于同生期或成岩早期。②膏泥岩孔隙流体的黏滞流动。孔隙流体能增加声波的黏滞吸收衰减，表现为孔隙中饱和水的岩样比干岩样的频散度或波速变化要大［3］。③三轴加载下的应力滞回性（应力/应变非线性）。因此，不同频率膏泥岩波速变化可以通过频散方程进行外推，其结果的可信度可以通过应用效果进行判定。频散方程主要考虑的是散射和岩石自身属性，表现为Q值的变化，未考虑其他因素，故具有一定精度，样品视频散程度要低于实际频散程度。

频散度

频散方程

频散误差

式中：f1，f2为不同频率，Hz；v1，v2为不同频率下的波速，m/s；vpmax，vpmin分别为纵波最大和最小速度，m/s；Dp为频散度，%；Q为品质因子；D为频散误差，%。

2 实验结果

虽然本次研究主要模拟地层条件下声波的频散效应，但实验中对逐步提高温度和压力多个条件下的声波速度和品质因子都进行了测试。前人研究表明，温度升高，膏岩强度和声波波速都会降低，高温（120℃）会导致石膏晶型转变，由二水石膏（CaSO4·2H2O）转变为半水石膏（CaSO4·0.5H2O），声学参数发生显著变化［9］。但本次研究最高温度只有85℃，且样品主要含硬石膏。硬石膏属正交晶系，不含结晶水，3个二次轴（a，b，c）相互垂直（a⊥b⊥c）且彼此不等（a≠b≠c），对声波的各向异性增强。由于膏泥岩相对致密，温度（85℃范围内）不会使石膏发生晶型变化，更不会使膏泥岩产生滑移系，因而理论上讲温度对膏泥岩岩样波速的影响不明显。对三组净围压（30MPa，40MPa，50MPa）进行对比发现，在地层温度（85℃）下纵波波速只比常温下降低了0.4%～0.9%，膏质泥岩（泥质体积分数＞50%）中降幅最大样品波速从3 748m/s下降到3 714m/s，降幅最小样品波速从2 306m/s下降到2 290m/s；硬石膏泥岩（硬石膏体积分数＞50%）中降幅最大样品波速从5 434m/s下降到5 387m/s，降幅最小样品波速从5 390m/s下降到5 366m/s，因而温度效应可以忽略。温度对品质因子的影响相对杂乱，相同净围压下不同温度品质因子变化幅度为5%～7%。在净围压增加至50MPa的过程中，纵横波波速值和品质因子都增加，纵波波速值增量为2.7%～8.4%，硬石膏泥岩的波速值较大（平均为5 780m/s），因而波速升高比例相对较小，而膏质泥岩中波速值较小（平均为3 951m/s），因而波速升高比例相对较大。纵波品质因子变化幅度在27%～58%，品质因子的升高表明声波的衰减逐渐减弱，由频散方程也可以看出声波的频散同样在减弱，模拟地层条件下各岩样品质因子的分布范围为6.34～18.12，平均为10.79。

3 频散公式外推

室内岩石声波测试频率为50～2 000 kHz［6］。由于波速为频率和波长的乘积，要想获得室内岩心完整波长就需要进行高频测试，而对测井（20 kHz）或地震（0.1 kHz）的频散研究主要以室内高频测试为基准，然后通过频散公式或特定模型［7，10-12］进行外推。前人研究表明，在饱和水条件下波速值由实验测试频率向20 kHz转换后，泥岩的频散要高于砂岩［8］。本次实验中声波测试采用1 000 kHz频率，利用频谱比法计算出的Q值代入公式（2）计算出20 kHz频率下的声波速度并进行频散分析，转化后声波速度降低。通过ΔT=304 800/vp（ΔT为声波时差，μs/ft；vp为纵波波速，m/s），将波速转化为时差后的结果与实验值及X井古近系膏泥岩层的纵波时差值进行统计对比（表1），结果可见外推值与声波测井值极为接近，而与1 000 kHz高频测试值具有一定差距。

表1 不同频率下纵波时差统计对比Table 1 Com parison of comp ressionalwave slowness time under different frequencies

4 频散对比及表征

4.1 频散度及频散误差对比

张元中等［6］对砂、泥岩的频散度研究表明，砂岩（孔隙中饱和水）由1 000 kHz外推到20 kHz后频散度为13%～22%；泥岩由1 000 kHz外推到20 kHz后频散度为4.00%～17.74%，样品间变化幅度较大。本次实验中膏泥岩（孔隙中饱和水）的频散度（图2）为7.4%～24.4%，平均为15.12%。由于是在模拟地层条件下，因此品质因子比较高。通过图3可以看出：20 kHz条件下的声波波速明显低于1000 kHz条件下的声波波速，各样品平均频散度误差较大，达到12.93%，因而，进行转换后波速值会发生巨大的变化，膏泥岩样品1 000 kHz测试得到的声波波速一般不能直接应用到其他实验力学参数（动静弹性参数及强度参数）或油田测井（20 kHz）计算的力学参数和预测中。

图2 膏泥岩纵波频散图Fig.2 Compressionalwave dispersion of gypsum mudstone

图3 频散波速对比及频散误差Fig.3 Com parison of dispersivewave velocity and er ror

4.2 品质因子对频散方程的另一种表征

考虑膏泥岩样品的品质因子、泥质和石膏含量等因素来分析2种频率下的声波波速变化。由图3可看出，品质因子大小与声波速度无关，例如图1中天蓝色样品的品质因子很小但波速很高，紫色样品的品质因子很大但波速较低。图4表明，品质因子为声波降低幅度的函数。由公式（2）可知，品质因子其实就是2种频率下声波波速比值的函数，而图4其实就是公式（2）的另一种表征，但是它可以更直观地表现出该区膏泥岩在模拟地层条件下随着品质因子的提高，声波的频散和衰减减小，同时声波的降低幅度会降低，其中品质因子的极限值（150 000［5］）为铝样。从图1曲线及图例中还可以发现岩性对声波速度具有一定影响，石膏含量高则声波速度相对增高，岩性与品质因子不服从正相关或负相关关系。

图4 品质因子与纵波降幅关系图Fig.4 Relationship between quality factor andcom pressionalw ave decline

4.3 品质因子影响因素

品质因子对研究声波频散非常重要，因此有必要讨论其影响因素［13-14］。该区膏泥岩品质因子的主要影响因素是泥质含量、石膏含量、孔隙度及密度，当然其他成分或地质条件如非均质性及弱面等也是造成品质因子复杂的重要原因，但笔者主要基于完整取心岩样进行评价。通过与品质因子拟合可以发现一个规律，上述4个因素中有3个（孔隙度除外）在拟合过程中是先降低后升高，且存在一个品质因子最低值点。由于膏泥岩样品主要含硬石膏和泥质，因而石膏质量分数约为35%时出现最低值，泥质质量分数约为55%时出现最低值，密度为2.5 g/cm3时出现最低值。泥岩的密度很小，主要为2.3g/cm3，硬石膏的密度很大，较纯的无水石膏密度都为2.9g/cm3以上，而密度为2.5 g/cm3的岩样主要为泥质和硬石膏互层段，等同于前面的低值点，因此，在该区当泥质质量分数为55%、石膏质量分数为35%及密度为2.5 g/cm3时均反映出同一品质因子的最低值点。同时加上其他沉积物的组合可能会造成较强非均质性，这些因素均可造成声波频散的加强。孔隙度与密度的关系为：孔隙度=-16.09×密度+46.55，R=0.967（密度为2.35～2.90 g/cm3；孔隙度，%）。密度是孔隙度的良好线性表征，品质因子随孔隙度的增加而减小，但没有出现最低值，不过孔隙度曲线在6%～8%附近逐渐趋于平缓。对拟合的样品统计可以发现，样品泥质质量分数平均为52%，也就是大部分样品泥质含量都很高，所以孔隙度集中的区域（6%～8%）对应着上述4个因素的品质因子最低值点。结合前面频散度的计算结果可以大致将本区古近系地层膏泥岩纵波频散强度划分为Ⅰ，Ⅱ，Ⅲ共3个等级（表2）。

表2 膏泥岩纵波波速频散等级划分Table 2 Division of compressionalwave velocitydispersion of gypsum mudstone

5 频散效应在横波时差预测中的应用

油田施工是一个准静态过程［15-16］，在确定套管强度、岩石强度、钻井液密度及压裂施工参数等方面都需要获得单井各层段的岩石静力学参数，而根据取心岩样进行的力学实验分析则无法对单井进行连续力学参数解释，只有依靠声波计算方可得到动力学参数，然后再进行动静参数转换才能最终获得各井连续力学参数测井解释剖面。实验室高频声波测试结果与油田声波测井频率不同，直接将实验室测试结果代入静力学参数的计算或预测中可能会产生较大误差，因此要考虑频散。考虑频散的一个重要因素是横波时差的预测。横波时差是预测众多力学参数的一个重要因子，但对于较浅地层或新区往往没有这些资料，只有在声波全波列或偶极横波资料中才有，此时可以根据纵横波时差拟合进行预测。本次实验的高频测试值拟合结果如图5（a）（1 000 kHz）所示；考虑频散时外推值的拟合结果如图5（b）（20 kHz）所示。对比这2幅图可以看出，两者的纵横坐标值差异较大，20 kHz的数据离散化程度明显要比1000 kHz高，且数据之间的分异（虚线）不明显，反映了更为真实的地层条件下纵横波时差之间的关系。

由于图5并不能定量表示频散计算值与原数据值之间分别拟合对预测值之间相对误差的影响，考虑到膏泥岩层段的纵波时差主要集中在50～100μs/ft，部分分布在100～140μs/ft，因此在这个区间内将2种频率条件下的纵横波拟合结果进行对比（图6）。可以看出，随着纵波时差的增加，起初两者计算的横波时差之间的差值逐渐减小，而后增大。通过计算，在纵波时差为50μs/ft（5.14%）时误差最大，纵波时差为90～100μs/ft（0）时误差最小，纵波时差为140μs/ft时误差为-2.41%，该范围平均相对误差仅有2%。由图5可知横坐标向左表明石膏含量增加，由于纵波时差为50μs/ft处预测的横波时差误差相对较大，因此，根据纵波时差预测的横波时差误差整体随着石膏含量的增加而变大，但对于本区古近系地层来说，该误差值并不大，表明频散对纵波或横波时差影响较大，但对它们之间的预测值误差影响不大，因而可近似利用室内1 000 kHz纵横波时差关系近似代表20 kHz纵横波时差关系，但横波时差同时也参与其他力学参数如弹性模量、剪切模量、体积模量、泊松比、抗压强度及地应力等的计算或预测，此时由于影响较大需进行频散校正。

图5 纵横波时差拟合关系对比Fig.5 Comparison of the fitting between compressionalwaveslowness timeand shear waveslowness time

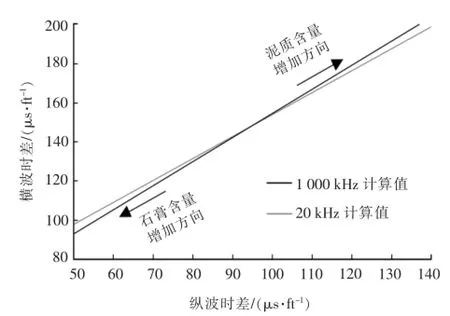
图6 频散计算值与原值分别拟合对比Fig.6 Comparison between the dispersion calculation value and the original value

6 结论

（1）温度为25～85℃时，膏泥岩在相同净围压下波速变化可以忽略，品质因子变化范围为5%～7%。当增加净围压及温度至地层条件时，纵波波速增量为2.7%～8.4%，品质因子增量为27%～58%。1 000 kHz和20 kHz频率条件下，膏泥岩频散度为7.4%～24.4%（平均值为15.12%），频散度较大，与泥岩（饱和水）类似。

（2）探讨了研究区膏泥岩品质因子影响因素，按由高到低的顺序将该区古近系膏泥岩纵波值划分为Ⅰ，Ⅱ，Ⅲ共3个频散等级，为该类型岩石更深入研究提供了参考。

（3）1 000 kHz和20 kHz频率条件下，当利用纵波时差对横波时差进行预测时，纵横波时差值极为接近（平均相对误差仅2%），因此可通用，但在具体力学参数计算或预测中，较高的频散度会使纵横波时差值本身发生较大变化，此时应进行频散校正。

［1］金之钧，周雁，云金表，等.我国海相地层膏盐岩盖层分布与近期油气勘探方向［J］.石油与天然气地质，2010，31（6）：715-724.

［2］刘雁婷，傅恒，陈骥，等.塔里木盆地巴楚—塔中地区寒武系层序地层特征［J］.岩性油气藏，2010，22（2）：48-52.

［3］Rios A，Roegiers J.Dilatancy criterionapplied forborehole stability during drillingofsalt formations［R］.SPE 153627，2012.

［4］《中国科学》杂志社.上地壳低频地震波频散现象的物理学机制被揭示［J］.科学通报，2010，55（34）：3350.

［5］汪瑞良，曾驿，刘军，等.珠江口盆地东部碳酸盐岩品质因子测试与分析［J］.中国海上油气，2011，23（2）：81-84.

［6］张元中，楚泽涵，李铭，等.岩石声频散的实验研究及声波速度的外推［J］.地球物理学报，2001，44（1）：103-110.

［7］巴晶.双重孔隙介质波传播理论与地震响应实验分析［J］.中国科学：物理学力学天文学，2010，40（11）：1398-1409.

［8］贾立坤.粘弹性介质地震波数值模拟［D］.北京：中国石油大学，2011：5-11.

［9］俞凌杰，张文涛，范明，等.膏岩三轴压缩试验及高温相变特征研究［J］.岩石力学，2012，33（11）：3318-3322.

［10］杨午阳，杨文采，刘全新，等.三维F-X域粘弹性波动方程保幅偏移方法［J］.岩性油气藏，2007，19（1）：86-91.

［11］陈可洋.井间弹性波波场散射特征数值模拟分析［J］.岩性油气藏，2011，23（3）：91-95.

［12］陈可洋.高精度地震纯波震源数值模拟［J］.岩性油气藏，2012，24（1）：84-91.

［13］刘树根，单钰铭，黄思静，等.塔河油田碳酸盐岩储层声学参数特征及变化规律［J］.石油与天然气地质，2006，27（3）：399-404.

［14］李亚林，贺振华，黄德济，等.露头砂岩纵横波衰减的各向异性实验研究［J］.石油地球物理勘探，1999，34（6）：658-663.

［15］Bloch M，Gupta A A.new strategy fornear real-time prediction of borehole stability［J］.Journalof Canadian Petroleum Technology，2001，40（4）：41-478

［16］周文，闫长辉，王世泽，等.油气藏现今地应力场评价方法及应用［M］.北京：地质出版社，2007：110-130.

图版Ⅰ

（本文编辑：杨琦）

Com parative study of high frequency acoustic wave testand dispersion extrapolation ofgypsum mudstone in simulated formation

LIShuanggui1，2，ZHANG Jun2，YIHao2，ZHOUW en3，SHAN Yum ing3，YIN Shuai3（1.Schoolof Petroleum Engineering，SouthwestUniversity of Petroleum，Chengdu610500，China；2.Research Instituteof Engineeringand Technology，NorthwestOilfield Company，Sinopec，Urumqi830011，China；3.Collegeof Energy Resources，Chengdu University of Technology，Chengdu610059,China）

In order toobtain the transformational relationsbetween shearwave slowness timeand compressionalwave slowness timeand otherstaticsparametersof thegypsummudstoneofPaleogene in A areaof Tarim Basin at20 kHz,we conducted indoor 1 000 kHz high frequency acousticwave test,and extrapolate the acoustic wave velocity at 20 kHz based on the tested acousticwavevelocity,quality factorand dispersion equation.Thecomparativeanalysisof theacousticwave or acousticwave slowness time at these two kindsof frequencies shows that the compressionalwave slowness time is closer to logging compressionalwave slowness time valueunder simulated formation condition;thewave velocity and quality factor changeslightlywithin 85℃,the changesofwavevelocity canbe ignored,and thequality factor ranges from 5%to7%;both thewave velocity and quality factor increasewith the increasingofnetconfining pressure;comparingwith compressional under simulated formation conditions and atmospheric pressure,the compressional wave velocity increment is 2.7%to 8.4%,and the compressional wave quality factor increment is 27%to 58%,gypsum mudstone dispersion degree is7.4%to24.4%（average15.12%）,with relatively largedispersion degree.By using thedeformation ofdispersion equation,we proposed an intuitiveexpression between quality factorandwave velocity declineofgypsum mudstone under simulated formation condition.According to the influencing factors of gypsum mudstone quality factor, thecompressionalwaveofgypsummudstonewasdivided intoⅠ,Ⅱ,Ⅲthree levelsofdispersion from high to low,atlast dispersion effectwas discussed in theapplication ofshearwave slowness time prediction.The results show thatunder the conditionsof1 000 kHz and 20 kHz frequency,theaverage relativeerrorofshearwave slowness time predicted by compressionalwaveslowness time isonly2%within thevariation rangeofgypsummudstoneacoustic time,and theerror has the trend of increasewith the increasingofgypsum content.The fitting formula of compressionalwave slowness to shearwave slowness can beapplied to the prediction ofshearwave slownessunder the two kindsof frequencies.Because the dispersion degree of gypsum mudstone is larger,and the acoustic slowness varies greatly under the two kinds of frequencies,so dispersion calibration should beapplied in theactualapplication.

formation conditions；gypsum mudstone;acoustic wave；wave velocity dispersion；compressional wave slowness timeand shearwave slowness time；quality factor

P631.3 < class="emphasis_bold">文献标志码：A

A

1673-8926（2014）01-0110-06

2013-06-04；

2013-08-10

国家“十二五”重大科技专项“缝洞型碳酸盐岩油藏高效酸压改造技术”（编号：2011ZX05014-006）资助

李双贵（1979-），男，高级工程师，西南石油大学在读硕士研究生，研究方向为钻井技术研究。地址：（830011）新疆乌鲁木齐市长春南路466号B503室。电话：（0991）3161185。E-mail：lishuanggui2004@126.com。