基于无迹卡尔曼滤波的四旋翼无人飞行器姿态估计算法

朱 岩，付 巍

（1.北京长城计量测试技术研究所，北京 100095；2.中北大学计算机与控制工程学院，山西太原 030051）

0 引 言

姿态解算的精度是实现四旋翼无人飞行器稳定飞行的前提［1，2］.目前，通常采用陀螺仪获得飞行器的姿态角.但陀螺仪存在漂移的问题，长期测量精度较差，因此需要对陀螺仪输出的数据进行有效的数据处理才能获得可靠和稳定的姿态角信息.陀螺仪输出的数据通过运动学微分方程，可以推导出载体的姿态角，其观测方程具有非线性的特点.扩展卡尔曼滤波算法是常用的解决观测方程非线性问题的算法.扩展卡尔曼滤波算法将非线性方程进行泰勒级数展开，去掉二阶以上的高阶项，使非线性方程线性化，其优点是运算速度快，实时性强，但估计精度较低［3］.为了提高飞行器的姿态估计精度，本文利用无迹卡尔曼滤波算法实现飞行器的姿态估计.无迹卡尔曼滤波算法在姿态角的估计值附近进行确定采样，得到一些采样点，这些采样点被称为Sigma点.在无迹卡尔曼滤波算法中，状态分布采用高斯随机变量表示，通过采用一些确定的Sigma点来描述高斯随机变量的特征.Sigma点集合具有和高斯随机变量相同的均值和方差.这些采样点通过非线性函数传播后，后验均值和方差可以达到2阶精度，而扩展卡尔曼滤波算法只能达到1阶精度［4］.无迹卡尔曼滤波算法不同于扩展卡尔曼滤波算法之处在于无迹卡尔曼滤波算法不是对非线性函数的近似，而是对状态随机变量分布的近似，它使用真实的非线性模型，因此，无迹卡尔曼滤波算法的精度和鲁棒性都强于扩展卡尔曼滤波算法.

1 四旋翼无人飞行器姿态解算模型的建立

四旋翼无人飞行器姿态解算是将飞行器上惯性单元的输出，实时转换成飞行器的姿态，即飞行器的载体坐标系（b系）相对于导航坐标系（n系）的角位置.

载体坐标系（b系），是固定在载体上面的坐标系，其原点在载体的质心处，OX b沿载体横向指向右，OY b沿载体纵向指向前，OZ b垂直于OX b Y b指向上.导航坐标系（n系），是用来表示载体所处位置的坐标系，其原点选在载体的质心处，OX n指向东，OY n指向北，OZ n沿垂直方向指向天，通常称为东北天坐标系［5］.导航坐标系与载体坐标系如图1所示.根据载体坐标系和导航坐标系之间的相对角位置关系，可以定义飞行器的3个姿态角.这3个姿态角分别为：俯仰角φ、横滚角ψ、偏航角γ，如图2所示.

图2 导航坐标系与载体坐标系之间转换角的关系示意图Fig.2 Schematic diagram of the angle conversion relations between carrier coordinates and navigation coordinates

图1 导航坐标系与载体坐标系示意图Fig.1 Schematic diagram of carrier coordinates and navigation coordinates

由四旋翼无人飞行器上的三轴陀螺仪可以得到飞行器相对于导航坐标系的角速度ωnb＝［ωnbx，ωnby，ωnbz］T，利用欧拉角法可得到飞行器的姿态运动学方程［6］.

四旋翼无人飞行器上的三轴陀螺仪在每一个采样时刻可以同时得到当前时刻飞行器的姿态角和姿态角变化率的信息.利用三轴陀螺仪测得的被噪声污染的角速度信息，结合数据处理算法就能够估算出飞行器当前的姿态角，实现对飞行器的姿态估计.

2 四旋翼无人飞行器姿态估计算法

2.1 系统状态方程

根据飞行器姿态解算模型，可建立系统状态方程和观测方程.

W（k）为第k个采样时刻的系统噪声向量；V（k）为第k个采样时刻的观测噪声向量.

2.2 无迹卡尔曼滤波算法

为了提高飞行器姿态估计精度，提出利用无迹卡尔曼滤波算法对安装于飞行器上的三轴陀螺仪输出的数据进行处理，解算出飞行器的姿态角.

无迹卡尔曼滤波算法单步流程如下：

假设在第k个采样时刻，系统状态的估计值表示为）；通过预测得到下一采样时刻（即第k＋1次）的系统状态的估计值表示为（k＋1｜k）；经过一次无迹卡尔曼滤波算法更新后，最终得到的在第k＋1个采样时刻，系统状态的估计值表示为X（k＋1）.

在第k个采样时刻，系统状态的估计误差协方差矩阵表示为P（k）；通过P（k）预测得到第k＋1个采样时刻系统状态的估计误差协方差矩阵表示为P（k＋1｜k）.经过一次无迹卡尔曼滤波算法更新后，得到的在第k＋1个采样时刻，系统的估计误差协方差矩阵表示为P（k＋1）.第k＋1个采样时刻系统状态的估计误差协方差矩阵P（k＋1）反映了在第k个采样时刻系统状态的估计值与系统状态的真实值的偏差.

确定Sigma点和各个Sigma点的权重

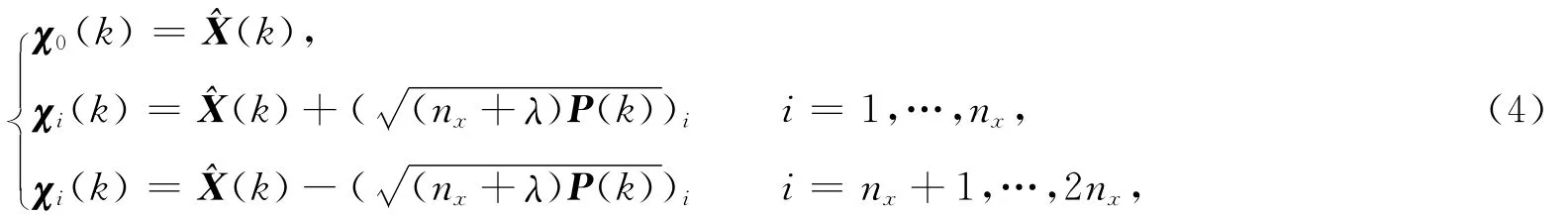
式中：n x表示系统状态向量的维数；λ＝ξ2（n x＋κ）－nx.

式中：ξ，κ，η为待选参数.ξ控制采样点的分布状态，调节ξ可以使高阶项的影响达到最小.ξ应该是一个较小的值，以避免状态方程非线性严重时采样点的非局域性影响［5］.κ的具体取值没有界限，对高斯分布的情况，当状态向量为单变量时，选择κ＝2；状态向量为多变量时，一般选择κ＝3－n x.η可以合并方程中高阶项的动差，调节η可以提高方差的精度［6］.

3 仿真实例

图3 俯仰角估计误差对比曲线Fig.3 The estimation error contrast curve of pitch angle

为了验证UKF算法的有效性和实用性，设置了飞行器和陀螺仪的仿真数值，通过仿真实验的方式比较EKF和UKF在相同条件下对飞行器姿态信息解算的精度.飞行器参数设置如下：飞行器的飞行倾角为10°，飞行器的三轴初始姿态角分别为1°，2°，5°，飞行器的转动惯量矩阵为J＝［3，0，0；0，9，0；0，0，9］.惯性单元参数设置如下：陀螺仪测量白噪声为0.6°／h，陀螺仪输出的初始姿态角速度分别为：0.01°／s，0.02°／s，0.03°／s，陀螺漂移在三轴上的初始值分别为1°／h，陀螺仪输出采样频率为100 Hz.依据上述初始条件，分别采用EKF和UKF对飞行器姿态角估计，估计结果如图3～图5所示.

由图3～图5可以看出，无迹卡尔曼滤波算法和扩展卡尔曼滤波算法都能实现对飞行器姿态角的估计，但在相同条件下，无迹卡尔曼滤波算法的估计精度和收敛速度都明显好于扩展卡尔曼滤波算法.

图4 横滚角估计误差对比曲线Fig.4 The estimation error contrast curve of roll angle

图5 偏航角估计误差对比曲线Fig.5 The estimation error contrast curve of yaw angle

4 结 论

研究了基于陀螺仪获取四旋翼无伤飞行器姿态解算模型的方法，建立了飞行器的系统状态方程和测量方程.为了提高飞行器姿态解算精度，提出了一种基于无迹卡尔曼滤波的姿态估计算法.理论分析和仿真表明，在相同条件下，基于无迹卡尔曼滤波的飞行器姿态估计算法的估计精度和收敛速度都明显好于扩展卡尔曼滤波算法.

［1］ 单海燕.四旋翼无人直升机飞行控制技术研究［D］.南京：南京航空航天大学，2008.

［2］ 聂博文，马宏绪，王剑，等.微小型四旋翼飞行器的研究现状与关键技术［J］.电光与控制，2007，14（6）：113－117.

Nie Bowen，Ma Hongxu，Wang Jian，et al.Study on actualities and critical technologies of micro／mini quadrotor［J］.Electronics Optics ＆Control，2007，14（6）：113－117.（in Chinese）

［3］ Julier S J，Uhlmann J K，Durrant－Whyte H.A new approach for filtering nonliear systems［J］.In：Proceedings of the American Control Conference，2005，11（2）：1628－1632.

［4］ Julier S J，Uhlmann J K.A new extension of the Kalman filter to nonlinear systems［J］.Proc.Of Aerosense：the 11th International Sumposium on Aerospace／Defence Sensing，Simulation and Controls，Orlando，Florida，2007，3（6）：118－124.

［5］ 马敏，吴海超.基于四元数自补偿四旋翼飞行器姿态解算［J］.制造业自动化，2013，35（12）：18－21.

Ma Min，Wu Haichao.Quaternion－based self－compensating attitude estimation for a quad－rotor aircraft［J］.Manufacturing Automation，2013，35（12）：18－21.（in Chinese）

［6］ 周晓尧，范大鹏，张智永，等.基于模糊加权EKF的车载光电桅杆姿态估计算法［J］.红外与激光工程，2011，40（8）：1569－1575.

Zhou Xiaoyao，Fan Dapeng，Zhang Zhiyong，et al.Attitude estimation algorithm of vehicle－bone optronics mast systems based on fuzzy weighted EKF［J］.Infrared and Laser Engineering，2011，40（8）：1569－1575.（in Chinese）