基于有限元方法的薄板超声Lamb波频散曲线计算

陈 亮， 王恩报， 马 豪， 董彦磊， 王 瑜

(电子科技大学 机械电子工程学院，四川 成都 611731)

0 引 言

超声Lamb波检测技术是薄板结构检测一种较为先进的无损检测技术，针对厚度在6 mm以下的薄板结构，利用换能器激励调制信号到薄板中，分析调制信号在传播过程中发生散射、反射和透射后的回波信号，对传播路径上的缺陷等信息进行检测[1-3]。由于Lamb波的频散特性，对于探伤参数选择，辨识性较好的模态选择以及结果分析的简易性等存在很多难题，在实际工业生产过程中的广泛应用产生了很大的阻碍[4]。

通过观察超声Lamb波的频散曲线不难看出，频厚积在1 MHz·mm范围附近，超声Lamb波主要以S0模态和A0模态进行传播；频厚积大于2 MHz·mm时，超声Lamb波将频散成诸多复杂的模态形式进行传播[5-6]。因此选取频厚积在1 MHz·mm范围时对于检测信息的分析的辨识性较好。通过分析检测信息中S0模态和A0模态的信号，对传播路径上的信息进行确定[7-10]。

本文主要采用有限元仿真的方法对薄铝板材料中超声Lamb波的传播进行模拟建模，通过提取仿真结果数据，计算群速度和相速度的大小，拟合绘制在2 MHz·mm以下的频散曲线，并通过Matlab对超声Lamb波的频率方程进行数值模拟，绘制铝板材料超声Lamb波的理论频散曲线。将两种方法计算所得频散曲线进行对比，验证有限元数值模拟的准确性。

1 超声Lamb波频散曲线理论求解

超声Lamb波在板中传播会出现频散现象，即会出现多模态现象。自由边界条件下Raleigh-Lamb频率特征方程为[11-13]：

对称模态

(1)

反对称模态

(2)

式中：p和q分别表示为：

(3)

波数k在数值上等于ω/cp，cp是Lamb波的相速度，ω为圆频率；cL和cT分别表示材料的纵波和横波速度；h为薄板的厚度，

其中，

E是材料的弹性模量；ν为泊松比；ρ为材料密度。

群速度cg可以通过相速度cp来求解，cg与cp有如下关系：

cg=dω/dk

(4)

将k=ω/cp代入上式得:

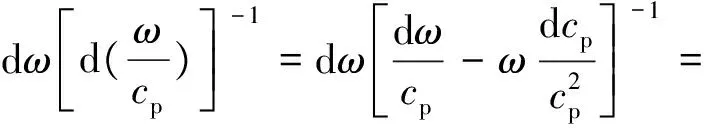
(5)

利用ω=2πf，上面的等式可以写做：

(6)

利用Matlab对频率特征方程以及群速度与相速度的关系式进行求解，绘制群速度和相速度的频散曲线[14]。

求解对象材料为铝板，密度为ρ=2 700 kg/m3，cL=6.27 mm/μs，cT=3.14 mm/μs。通过数值求解得到群速度和相速度的频散曲线分别如图1和图2所示。

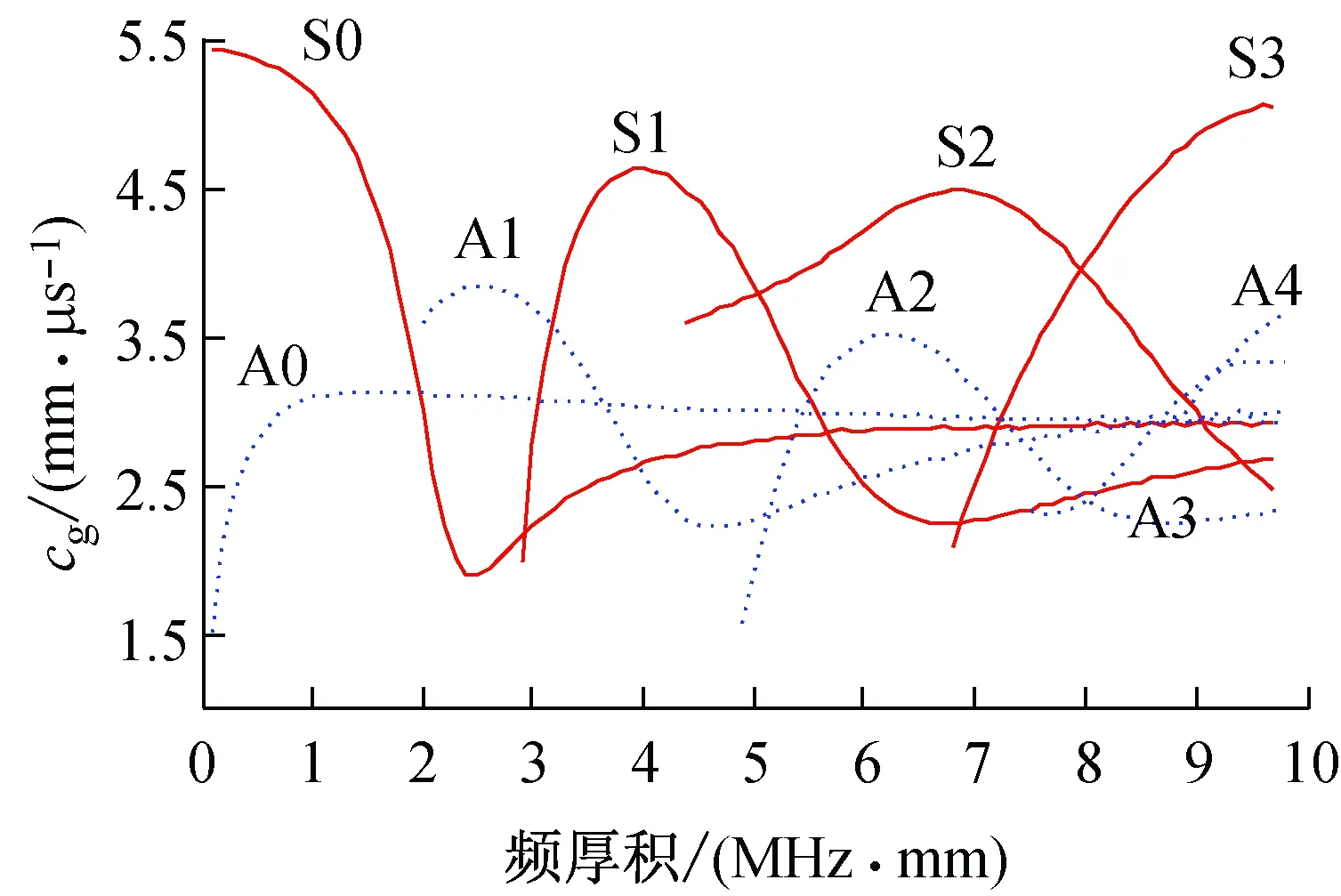
图1 群速度理论频散曲线

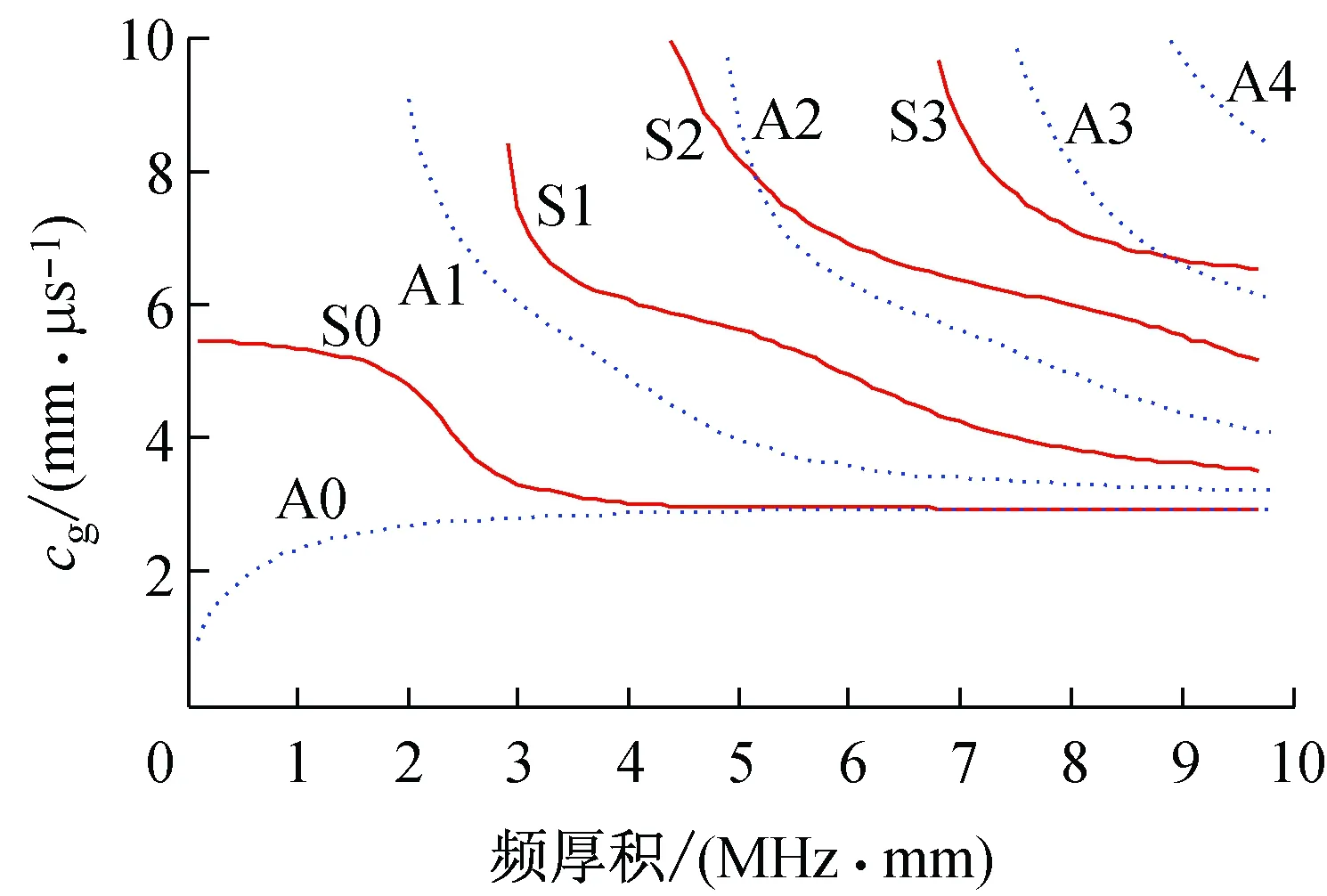
图2 相速度理论频散曲线

2 超声Lamb波在板中传播有限元模拟

2.1 材料参数确定

采用ABAQUS对薄铝板中超声Lamb波传播进行数值模拟。所采用铝板材料密度ρ=2 700 kg/m3，泊松比υ=0.33，弹性模量E=70 GPa。

2.2 激励信号选取

分别采用50，100，150，200，250，300，350，400，450和500 kHz的10种不同中心频率的5周期汉宁窗调制正弦信号作为激励信号。图3所示为中心频率为250 kHz的5周期汉宁窗调制信号。

2.3 有限元仿真计算群速度大小

建立厚度h=4 mm，长度x=300mm的铝板模型，激励信号采用上述中心频率250 kHz的5周期汉宁窗调制信号呈45°加载在模型左上角的集中力，接收点在激发点位置，采用四方形网格划分，模型图见图4。

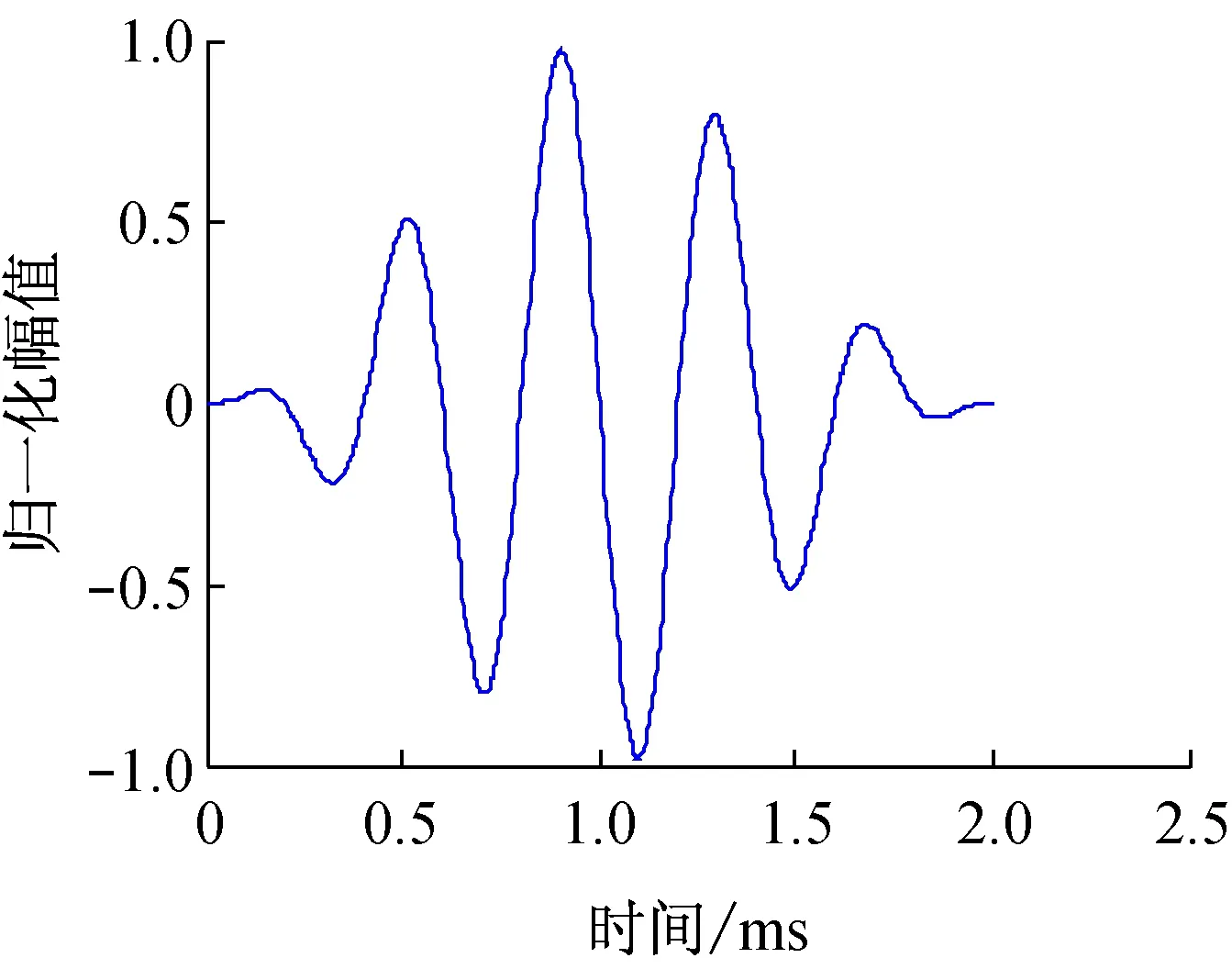
图3 250 kHz的5周期汉宁窗调制正弦信号

仿真结果接收到的时域波形图如图5所示。从激励信号到接收点收到回波信号的距离为600 mm。

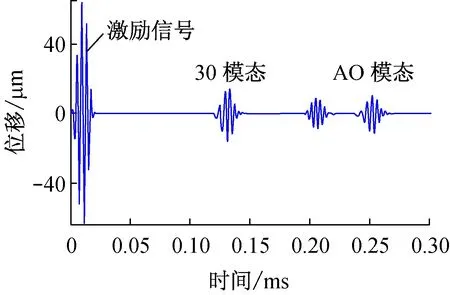
图5 仿真时域波形图(群速度计算)

采用10种激励信号，求出分别对应的S0、A0模态的群速度，同时与前面利用数值求解此材料参数铝板的理论群速度曲线相比较，对比结果如表1所示。

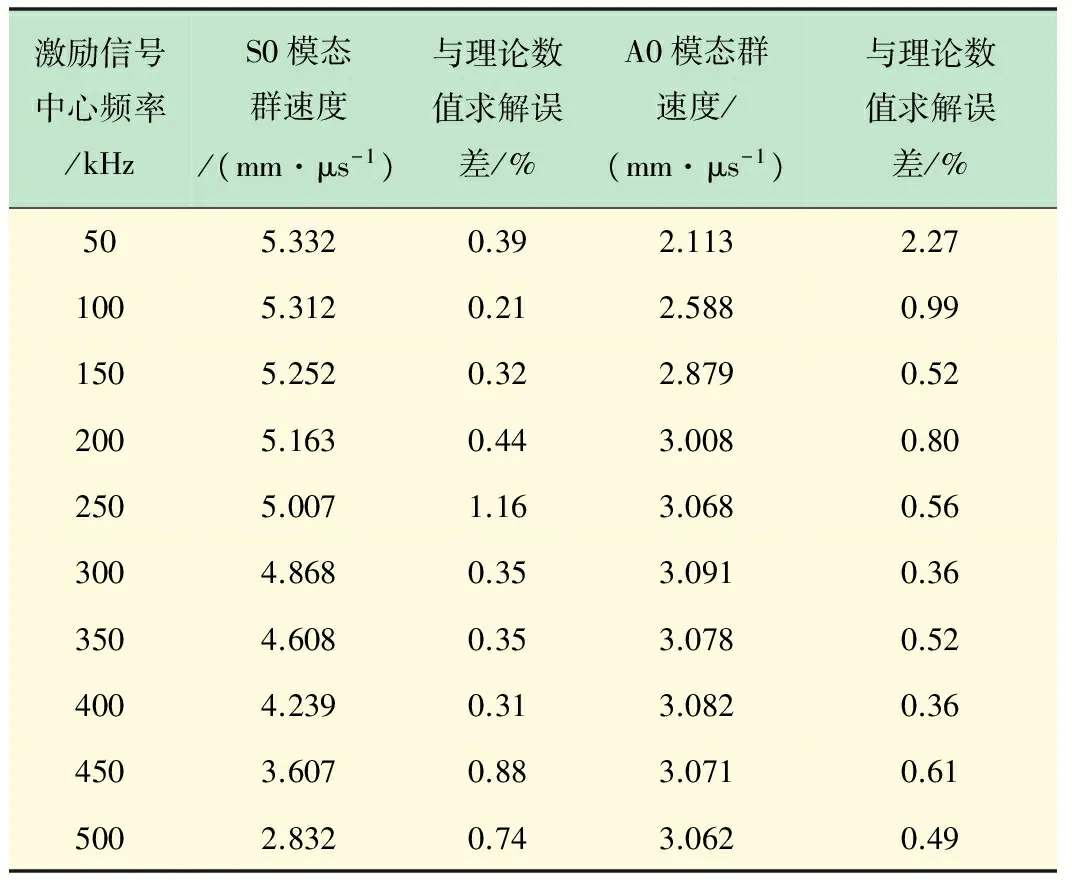
表1 有限元仿真计算群速度及其与理论数值求解误差

从表1可知，有限元仿真计算S0和A0模态群速度的相对误差均小于5%，因此可以验证对板中Lamb波传播频散现象有限元仿真群速度模拟的有效性。

通过表1中的数据可以绘制出通过有限元计算得出的频厚积在0.2～2 MHz·mm内A0模态和S0模态的群速度频散曲线，如图6所示。

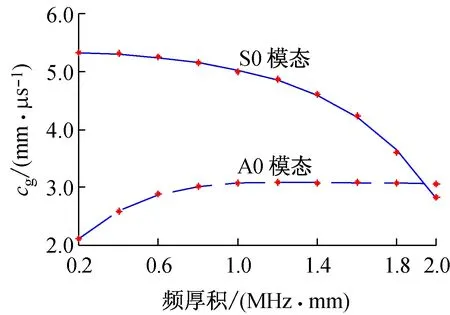
图6 有限元计算群速度频散曲线

2.4 有限元仿真计算相速度大小

建模厚度h=4 mm，长度=800 mm的铝板模型，激励信号采用上述中心频率250 kHz的5周期汉宁窗调制信号呈45°加载在模型左上角的集中力，信号接收点选取在距离激励触发位置400、410 mm的点位置，网格划分采用四方形网格划分，模型图见图7。

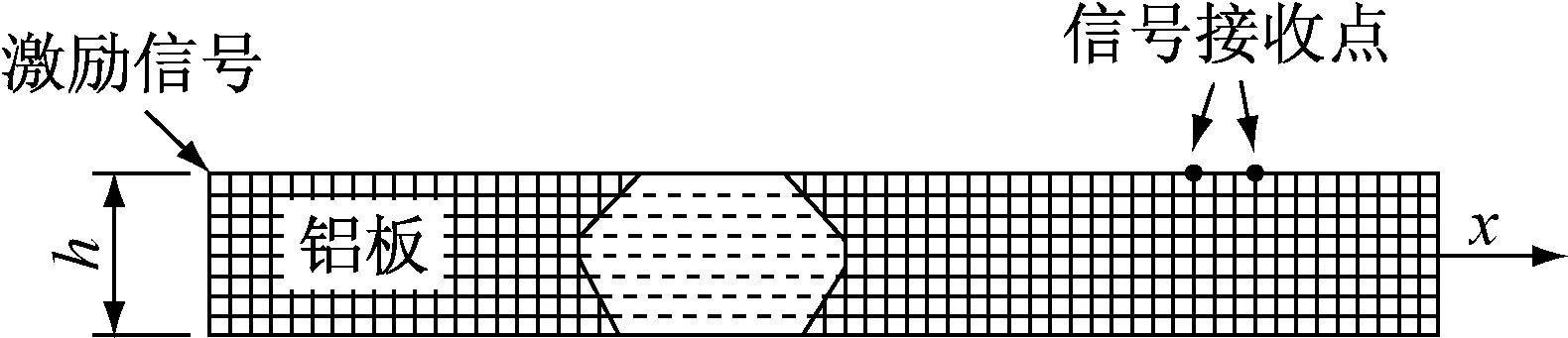
仿真结果距离激励信号400、410 mm距离的接收点接收的信号时域波形图如图8所示。

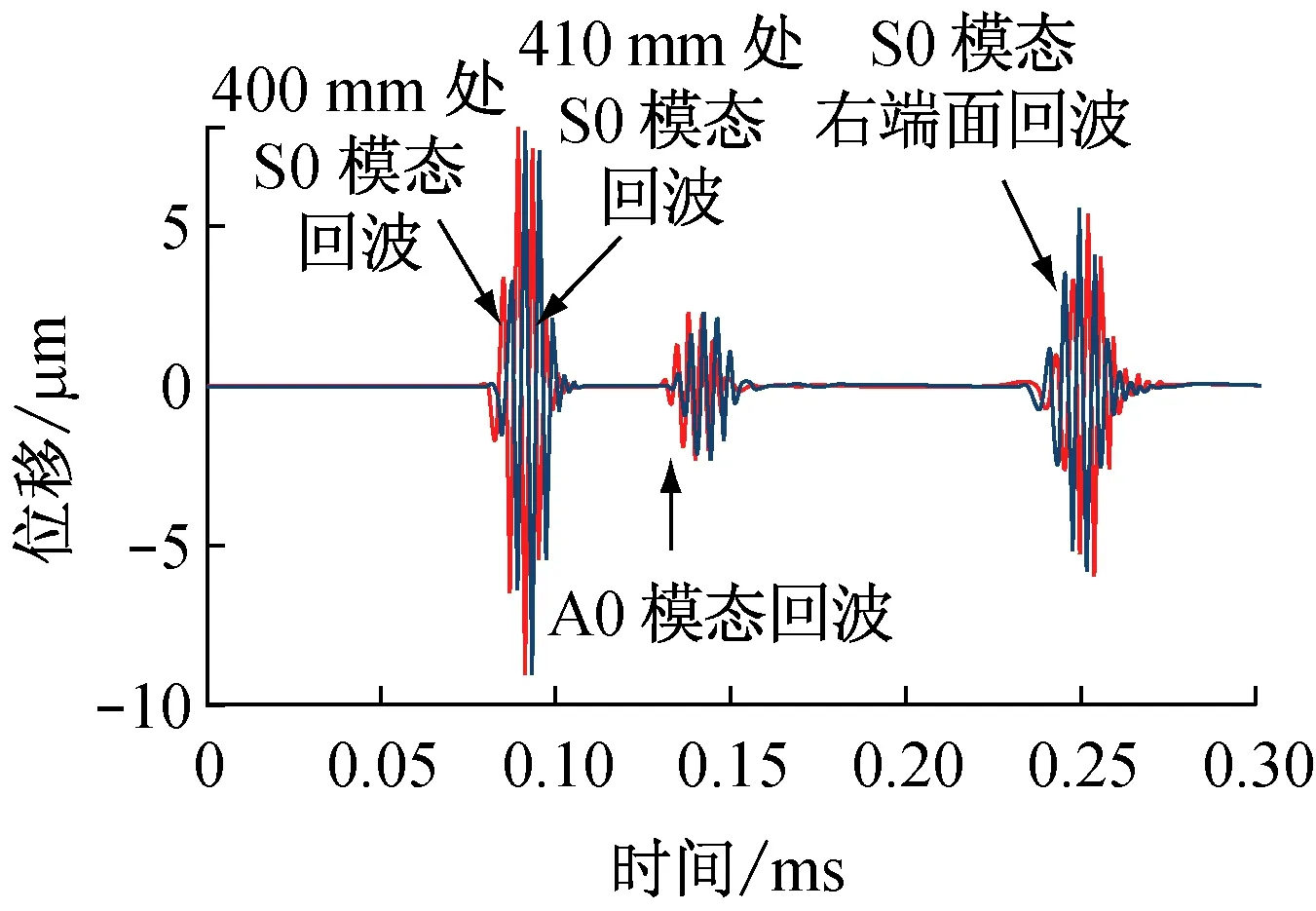
图8 仿真时域波形图(相速度计算)

计算A0和S0模态单一频率在经过400～410 mm这10 mm距离时所用的时间差。

与群速度有限元仿真计算相同，采用10种激励信号，求出分别对应的S0模态和A0模态的相速度，同时与前面利用数值求解此材料参数铝板的理论相速度曲线相比较，对比结果如表2所示。

从表2可知，有限元仿真计算所得S0和A0模态相速度的相对误差均小于5%，因此可以验证对板中Lamb波传播频散有限元仿真相速度模拟的有效性。

通过表2中的数据可以绘制出通过有限元计算得出的频厚积在0.2～2 MHz·mm范围内A0模态和S0模态的相速度频散曲线，如图9所示。

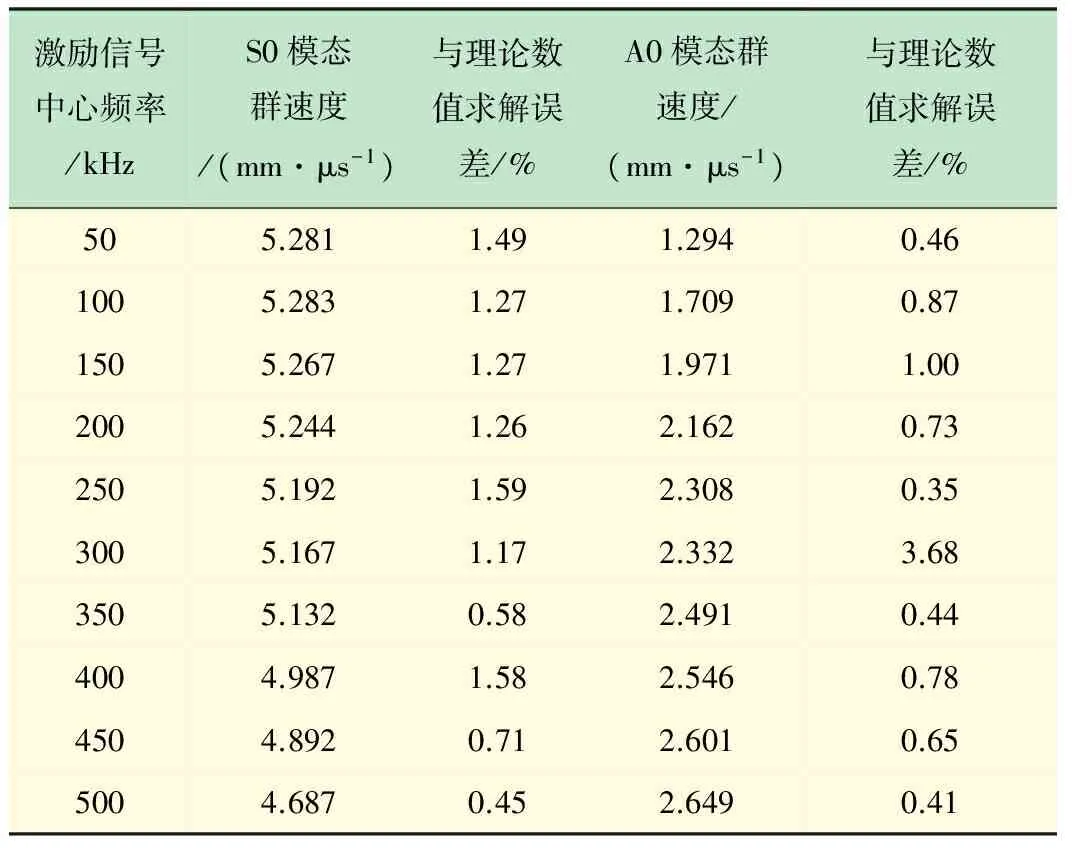
表2 有限元仿真计算相速度及其与理论数值求解误差

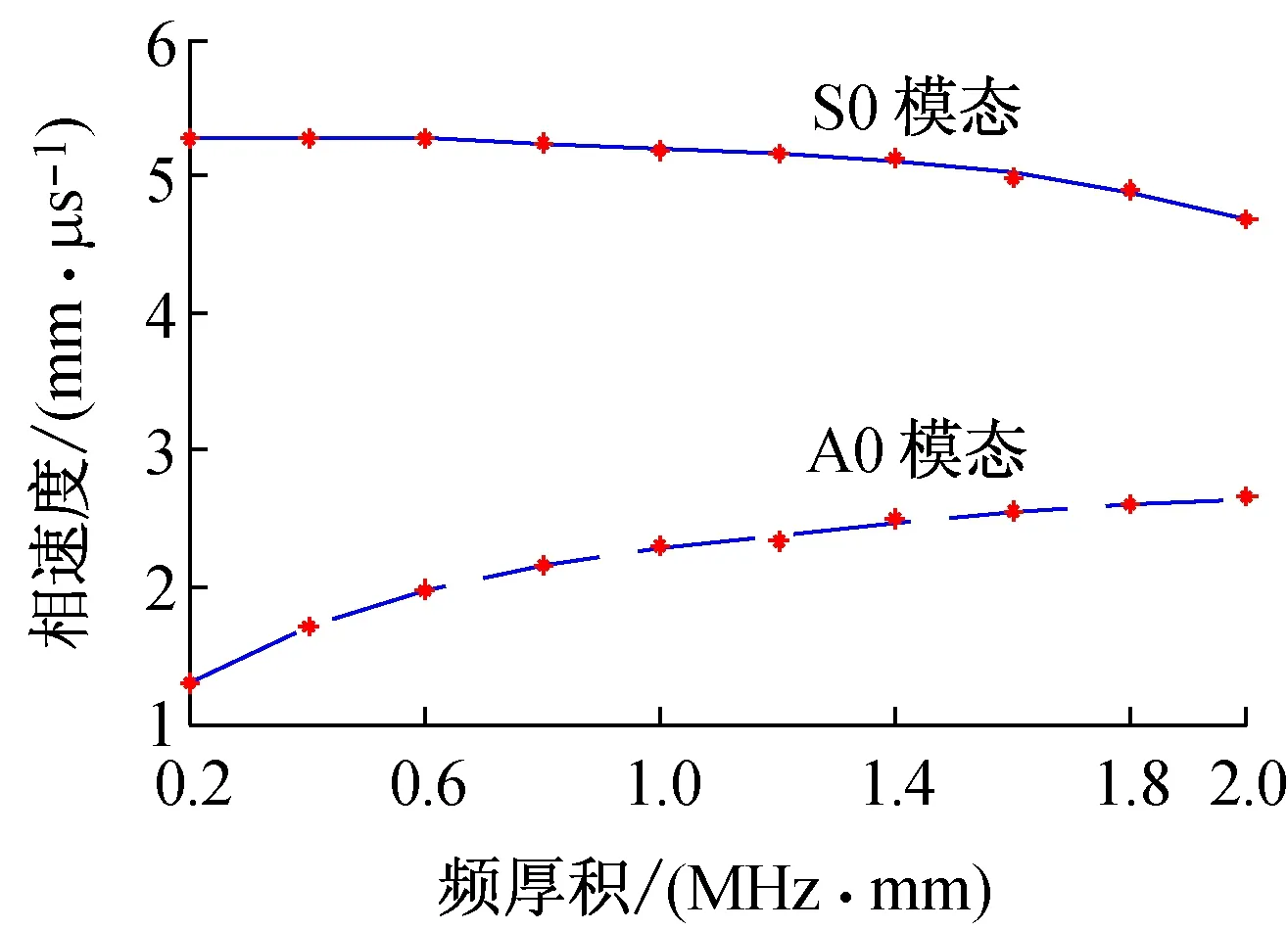
图9 有限元计算相速度频散曲线

3 结 语

通过有限元方法对薄板结构进行仿真，对超声Lamb的传播模式进行研究，得到以下结论：

(1) 对10组不同的频率对应的频厚积进行有限元仿真，对仿真结果进行计算，绘制了频厚积在0.2～2 MHz·mm范围内A0模态和S0模态的群速度和相速度的频散曲线。

(2) 求解超声Lamb波的频率方程，绘制超声Lamb波的理论频散曲线，将有限元方法绘制的频散曲线与其进行对比，证实了有限元方法的有效性。

同时，对于复合结构和非平面结构，很难建立相应的频散曲线数学描述方程，采用有限元方法可以得到相应的频散曲线，对此类结构的检测提供理论指导。

[1] 阎 石, 张海凤, 蒙彦宇. 利用Lamb波的薄板结构多点损伤识别试验[J]. 沈阳建筑大学学报(自然科学版), 2010, 26(4):777-782.

YAN Shi, ZHANG Hai-feng, MENG Yan-yu, Experimental Research on Multi-Damage Detection of Metal Plate Structure Using Lamb Wave[J]. Journal of Shenyang Jianzhu University (Natural Science), 2010, 26(4):777-782.

[2] 陆 希, 孟 光, 李富才. 基于Lamb波的薄壁槽状结构损伤检测研究[J]. 振动与冲击, 2012, 31(12): 63-67.

LU Xi, MENG Guang, LI Fu-cai, Lamb wave-based damage detection for a channel-like thin-wall structure[J].Journal of Vibration and Shock, 2012, 31(12): 63-67.

[3] Nayfeh A H, Chimenti D E. Free wave propagation in plates of general anisotropic media[J]. Journal of Applied Mechanics, 1989, 56(4):881-886.

[4] 陈 军, 李志浩, 林 莉,等. 铝板中Lamb波检测的实验研究[J]. 应用声学, 2011, 30(2):98-104.

CHEN Jun, LI Zhi-hao, LIN Li,etal. Experiment investigations of Lamb waves in an aluminum plate[J]. Applied Acoustics, 2011, 30(2):98-104.

[5] 李鸿源, 徐 鸿, 田振华. Lamb波损伤散射及损伤成像的模拟[J]. 无损检测, 2012, 34(9):12-15，26.

LI Hong-yuan, XU Hong, TIAN Zhen-hua. Detection of damages in plates based on symmetric lamb wave [J]. Nondestructive Testing, 2012, 34(9):12-15，26.

[6] 魏云飞，卢 超.薄板腐蚀缺陷Lamb成像检测的传播模式的有限元模拟[J].测试技术学报,2010,24(3):259-264.

WEI Yun-fei, LU Chao, Finite Element Modeling of Corrosion Image Detection Using Lamb Wave in Thin Plate[J]. Journal of Test and Measurement Technology, 2010,24(3):259-264.

[7] 艾春安, 王学勇, 刘 瑜. 薄板钢结构超声检测Lamb波激励与模态分析[J]. 噪声与振动控制, 2012, 32(1):137-140.

AI Chun-an, WANG Xue-yong, LIU Yu. Ultrasonic Detection of Lamb Wave Stimulation and Modal Analysis of Thin Steel Plate Structure[J]. Noise and Vibration Control, 2012, 32(1):137-140.

[8] 吴 斌, 周 伟, 郑 阳,等. 基于波结构的Lamb波单一模态激励仿真[J]. 无损检测, 2011,33(7):1-4，10.

WU Bin, ZHOU Wei, ZHENG Yang,etal. Excitation of single mode lamb wave simulation based on wave structure[J]. Nondestructive Testing, 2011,33(7):1-4，10.

[9] Mace B R, Manconi E. Modeling wave propagation in two-dimensional structures using finite element analysis[J]. Journal of Sound and Vibration, 2008, 318(4-5):884-902.

[10] Moser F, Jacobs L J, Qu J. Modeling elastic wave propagation in waveguides with the finite element method[J]. NDT & E International, 1999, 32(4): 225-234.

[11] 吴 斌, 周 伟, 何存富. Lamb波在搭接板中传播规律的数值仿真研究[J]. 压力容器, 2011, 28(6):24-30.

WU Bin, ZHOU Wei, HE Cun-fu. Experimental and Numerical Study of the Lamb Waves Propagation in Overlapping Plates[J]. Pressure Vessel Technology, 2011, 28(6):24-30.

[12] Terrien N, Osmont D, Royer D,etal. A combined finite element and modal decomposition method to study the interaction of Lamb modes with micro-defects [J]. Ultrasonic, 2007, 46(1):74-88.

[13] Diligent O, Grahn T, Bostr?m A,etal. The low-frequency reflection and scattering of the S0 Lamb mode from a circular through-thickness hole in a plate: Finite Element, analytical and experimental studies[J]. Journal of the Acoustical Society of America, 2002, 112(6):2589-2601

[14] 艾春安, 李 剑. Lamb波频率方程的数值解法[J]. 无损检测, 2005, 27(6):294-296.

AI Chun-an, LI Jian. Numerical Calculation for Lamb Wave Frequency Equation[J]. Nondestructive Testing, 2005, 27(6):294-296.