耦合潜源参数不确定性效应的地震海啸危险性分析——原理与方法

任鲁川，霍振香，洪明理

（中国地震局防灾科技学院，河北三河065201）

耦合潜源参数不确定性效应的地震海啸危险性分析
——原理与方法

任鲁川，霍振香，洪明理

（中国地震局防灾科技学院，河北三河065201）

总结基于数值模拟的地震海啸危险性分析的基本步骤，论述潜源位置界定原则、潜源参数取值方法、潜源地震海啸发生率估算方法，同时给出一种可以耦合潜源参数不确定性效应的地震海啸危险性分析方法。

地震海啸；危险性分析；不确定性；潜源参数；数值模拟

1 引言

目前，有两类地震海啸危险性分析方法：确定性方法和概率分析方法。概率分析方法又可分为两个亚类：基于场点海啸波高记录的经验统计方法和基于数值模拟计算的概率分析方法。其中，基于数值模拟的概率分析方法应用较为广泛，它尤其适用于历史海啸波高记录缺乏或较少的沿海地区地震海啸危险性分析。

基于数值模拟的地震海啸危险性分析与地震工程研究领域广泛采用的地震危险性分析有诸多异曲同工之处。在地震工程研究领域，地震危险性指，未来一定时期内，特定场点由地震引起的一定强度的地面运动的可能性，其中地面运动强度可用地面运动的峰值加速度和峰值速度表示，可能性可用超越概率或重现周期表示[1]。地震危险性分析大致包含三个环节：（1）界定未来一定时期内，可能对场点产生影响的潜在震源位置，并标定潜在震源参数；（2）建立地震波传播衰减关系式；（3）耦合场地效应，估计场点的地震危险性[2]。地震危险性分析中的一个重要问题是存在不确定性，部分学者[2-6]已就如何分析和诠释这种不确定性开展了一系列相关研究。

海啸的致灾效应取决于三个因素：（1）海啸引起的海水漫滩和淹地；（2）海啸波的冲击作用对结构的破坏；（3）海啸波对岸滩的冲蚀作用[7]。上面三个因素的致灾效应皆与海啸波高有关。在海啸研究领域，海啸危险性指，未来一定时期内，特定场点遭受一定强度海啸袭击的可能性，其中海啸强度可用海啸最大波高表示，可能性可用超越概率或重现周期表示。近年，有学者对基于数值模拟的地震海啸危险性概率分析中的不确定性问题进行了探讨。任鲁川等[8]（2012）指出，地震海啸危险性分析的不确定性源于地震海啸生成、传播、爬高过程分析中的不确定性因素，定性分析和定量评估这些不确定性因素的效应的方法，应是目前地震海啸危险性分析的一个重要研究方向。温瑞智等[9]（2012）分析地震海啸危险性分析中不确定性的主要来源时指出，不确定性的主要方面包括：确定潜在地震海啸源（以下简称潜源）的位置及地震类型、确定震级-频度关系中参数、采用经验公式确定断层参数、对断层破裂进行假设、数值模拟中采用的海水深度误差、数值模式中对传播原理进行假设产生的不确定性。Geist[4]等（2006）借鉴地震危险性分析中的方法，将不确定性划分为认识类不确定性和随机类不确定性；在其美国太平洋西北沿岸地区（the U.S. Pacific Northwest coastline）的地震海啸危险性分析研究案例中，他们采用了蒙特卡洛（Monte Carlo）随机模拟方法，为具有随机不确定性的地震断层位错参数取值。

综上，作者认为，基于数值模拟的地震海啸危险性概率分析中，如何耦合潜源参数取值不确定性效应，是目前需要深入探讨的一个重要问题。

本文首先总结基于数值模拟的地震海啸危险性分析的基本步骤；继而讨论潜源位置界定原则；然后论述潜源参数取值方法和潜源地震海啸发生率估算方法；最后，给出可耦合潜源参数不确定性效应的地震海啸危险性分析的方法和步骤。限于篇幅，拟另文介绍基于本文所提出方法的案例研究结果。

2 地震海啸危险性分析的基本步骤

综合相关研究[4,8-10]，归结地震海啸危险性分析的基本步骤如下：

（1）选定场点，界定潜在地震海啸源位置，并为潜源参数取值。

（2）计算海床同震位移场，推断相应的海啸波初始位移场。

地震海啸危险性分析中，目前通常采用半无限空间弹性位错地震断层模型计算海床同震位移场。该模型由Mansinha和Smylie[11]（1971）提出，后来Okada[12]（1985）又做了改进。在假设地震引起的海床变形极为迅速，且海水不可压缩的情形下，可以认为，在地震发生的瞬间，覆盖在海床上面的海水难以大规模流动，从而可以进一步认为，海水表面初始位移场即海啸波初始位移场与海床初始位移场一致。

（3）选用海啸数值模式，模拟计算海啸波传播过程。

目前模拟计算海啸波传播过程常用的海啸数值模式有：NOAA海啸研究中心(NCTR)开发的的MOST模式[13-16]、美国Cornell大学开发的的COMCOT模式[17-18]、日本Tohoku大学开发的的TUNAMI-N2模式[10]、我国国家海洋环境预报中心开发的海啸数值模式等[19]。

（4）遴选对场点海啸危险性有贡献的潜源。

选定临界海啸波高。从模拟计算结果中提取场点海啸波高数据。以hmax(r,r0,ψcsrit)≥hcrit（场点最大海啸波高超过临界海啸波高）为判据，遴选潜源。上式中，r，r0，hcrit，ψcsrit分别表示场点空间位置、潜源空间位置、临界海啸波高、与临界海啸波高对应的一组潜源参数。

（5）计算地震海啸发生率。

包括：（a）计算单个潜源的地震海啸发生率（下文简称单源地震海啸发生率），（b）计算所有潜源的地震海啸总发生率（下文简称地震海啸总发生率）。

以ψs表示一组潜源参数，以n(r,r0,ψs)表示位于r0潜源参数为ψs的地震海啸发生概率，以ψmsax表示与最大海啸波高的最大值相对应的一组潜源参数。

单源地震海啸发生率可表示为潜源参数空间的积分：

地震海啸总发生率可表示为潜源位置参数空间的积分：

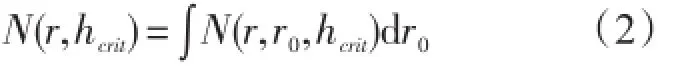
（6）估计场点地震海啸危险性。

假定场点遭受地震海啸袭击的事件为泊松过程，则在未来一定时期T内，场点地震海啸波高超越临界值hcrit的概率即场点地震海啸危险性可以表示为：

3 潜在地震海啸源位置界定原则

进行地震海啸危险性分析，需先划分相关研究海域的地震区（带），界定地震区（带）内的潜在震源位置，再界定潜在地震海啸源位置。

所谓地震区指，数十万乃至几百万平方千米的大区域范围内，地震活动和大地构造活动具有明显相关性的地区。同一地震区，地震活动的时间、空间、强度特征具有共性。所谓地震带指，同一地震区内，地震活动性和地质构造条件密切相关的地带。与地震区相比，地震带内地震活动在时间、空间、强度上的相关性更为密切，且震中分布相对密集成带[20]。区域地震活动性特征和地震构造环境特征是地震区（带）划分的基本依据。地震活动特征包括震中分布、震源深度分布、地震强度分布、地震频度分布等。地震构造环境特征包括活动构造特征、地壳深部结构特征、区域构造应力场特征和地球物理场特征。地震带是地震区内的次级单元。地震区内具有下述特点的地带常被界定为地震带：（1）现代构造运动性质和强度一致性较好或类似；（2）地震活动性（包括地震频度、最大震级、活动周期、古地震和历史地震重复间隔、应变积累释放过程等）相一致或一致性较好；（3）新生代以来地震构造应力场（包括断层节面性质、主压应力轴方位和倾角等）一致性较好；（4）其它典型分带特征，诸如活动构造带的边界、破坏性地震相对密集带的外包带或区域性深大断裂活动的影响带[20]。

海域地震区（带）划分，应遵循上述地震区（带）划分的一般原则。

潜在震源区指，未来一定时期内，可能发生破坏性地震（通常MS≥5.0）的地区。目前潜在震源区位置界定，主要依据两条基本原则即地震构造类比原则和地震活动重复原则。地震构造类比原则的含义是，某一地区历史上虽然没有强地震或中强地震的记载，但如果它与已经发生过同等强度地震的某一地区的构造条件类似，就可将其界定为同类震级上限的潜在震源区。特别的，已发现有古地震遗迹的地区，可界定为相当于最大古地震震级的潜在震源区。地震活动重复原则的含义是，历史上发生过强震的地区，可界定为具有同类震级或高于原最大震级的潜在震源区[20-21]。

潜在地震海啸源区位置界定，要遵循潜在震源区位置界定的一般原则，参照海域潜在震源区位置界定结果，但同时还必须参照产生海啸灾害的其它条件。

必须指出，产生海啸灾害的条件和产生海啸的条件不同。海啸是海水受到某种突然的扰动后，受扰动的海水在重力的作用下趋于恢复平衡，而形成的一种具有较长波长和较长周期的行波[7]。这里所说的突然的扰动可以来自于海底地震，以及海底火山喷发、海底滑坡、陆架或冰架垮塌，陨星落入海洋、海域核爆破等。海啸传播至近海和沿海区域，仍具有一定规模，才可能导致灾害的形成。海啸灾害历史资料显示，史上绝大部分导致重大灾害的海啸是由海底地震触发产生的。

人们通常将震级足够大（≥6.5级）、震源足够浅（浅源地震）、震中区域海水足够深，作为界定潜源位置的基本判据[22]。再者，海沟沉降带在潜源位置界定中广受关注[23-26]。根据震源所在的具体位置，海沟沉降带的地震可区分为板间地震和板内地震（包括海沟外脊、下降板块内和上覆板块内的地震）（见图1）。Satake和Tanioka（1999）[24]研究发现，触发海啸的板间地震，震源深度分布范围10—40 km；大多位于上覆板块的增生稧与沉降板块交接的部位，断层的错动方向随震源深度和沿断层走向改变;板内地震所触发的海啸在规模上可与板间地震等量齐观。Stephen Kirby等[25-26]（2010）的研究显示，海沟区域触发巨大海啸的地震，震级一般大于8.0级，地震断层破裂规模大于100 km，地震断层错动具有正断分量;断层倾角通常大于30°;较多位于海沟向海一侧的海沟外脊（the outer-rise）或海沟的外部斜坡(outer-trench-slope)区域;震源深度约在海底以下5—20 km;震中位于深水区域。

4 潜在地震海啸源参数取值

决定地震海啸规模的主要因素包括：潜源位置、地震能量、地震机制、震源深度等。地震海啸危险性分析中，通过为地震海啸数值模式输入不同潜源参数来体现上述因素的效应。潜源参数（以COMCOT模式[17-18]为例）（见图2）包括：（1）断层几何参数（断层的长度L、宽度W、断层走向角θ和倾角δ）；（2）地震参数（震中纬度和经度、震源深度、震级或断层位错、地震断层两盘间滑移角λ）。

4.1 断层几何参数和震中位置、震源深度及断层滑动角的取值

图1 海沟沉降带横剖面示意图（据文献24图1改绘）

一般说来，通过板块构造动力学、大地测量学、地震构造、地震活动性、海底地貌以及海域地球物理场等方面的研究，结合历史地震记录、历史海啸记录、海水深度资料的分析，可以界定出潜源的位置，同时获得分布其内的断层的几何参数信息，推断出断层长度、宽度、走向、倾向角等参数的取值。例如，NOAA海啸源工作组[23,25]，在其进行的西北太平洋区域的潜源研究中，正是基于该区域内海沟沉降带的地质特征和板块构造动力学特征，参照该区域1895年以来的历史地震海啸记录，沿着该区域内分布的海沟的延伸方向，将海沟沉降带的断层分段，推断各个断层段长度、走向和倾向角，估计各个断层段的宽度。

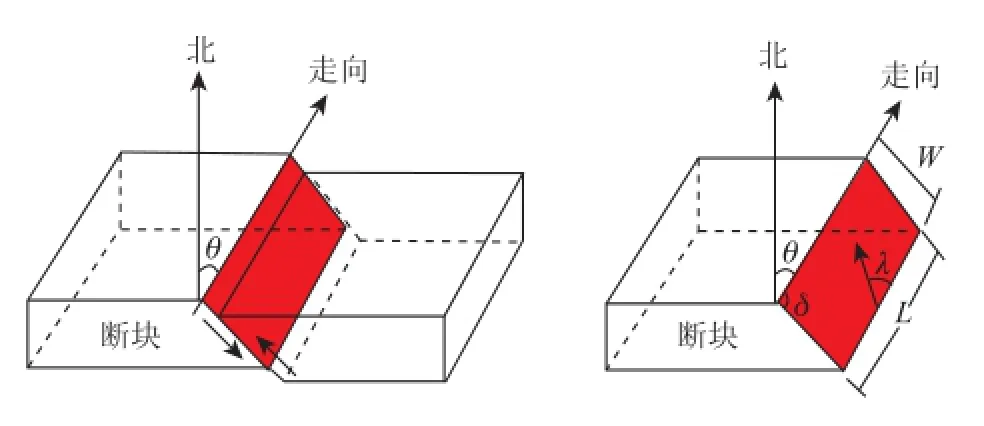
图2 地震海啸源参数

需要说明，未来地震所可能引起的断层错动宽度难以直接估计，通常进行间接估计。目前有两种间接估计的方法[27-28]：（1）根据同一潜在震源历史上发生的大地震的余震分布范围，进行大致估计；（2）基于统计分析得到的震级与断层破裂面积、或与断层长度、宽度之间的经验关系式，进行近似估计。

由于地震预测水平和历史地震记录数据的限制，抑或源于地震活动本身的复杂性，难以在地震发生之前，准确判定地震震中位置、震源深度、地震断层滑动方向。但是，一般说来，分析潜源的地震构造特征、历史地震活动特征以及震源机制解，可以在一定程度上对未来地震的震中位置、震源深度、地震断层滑动方向做出估计。

4.2 介质剪切模量的取值及矩震级与断层平均位错的换算

地震海啸危险性分析中，依据标准参考地球模型为潜源区介质剪切模量μ取值。然后，依据地震断层平均位错与震级或地震矩之间的关系式，计算出平均位错。

构造地震由地下岩石的突然错断引起。作为地震能量标度的地震震级与断层面的面积、地震孕育的深度、断层两盘相对错动的距离、断层滑移速率、岩石介质的剪切模量（shear modulus）有关[29]。人们常用地震矩或矩震级标度地震的大小。地震矩定义为：

式中，L表示断层长度，W表示断层宽度，D¯表示断层面上的平均位错，μ表示介质量剪切模量。H.Thomas.C等[30]给出矩震级与地震矩之间的关系为：

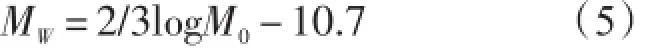
式中，M0的单位是牛顿·米。

已知地震断层长度、宽度和介质剪切模，利用式（4）和（5），可以进行地震的矩震级与地震断层平均位错之间的换算。

5 地震海啸发生率估计

要估计某一潜源地震海啸发生率，需先估计同一潜源强震发生率。目前地震危险性分析中强震发生率的估计，或采用基于G-R关系（古登堡-里克特震级频度关系）的概率估计模型，或采用基于特征地震的强震复发时间可预测模型。

概率估计模型由Cornell[31]（1969）提出，后经众多学者[20]加以改进，可以用来估计不同震级档次地震的发生率。该模型假设潜在震源区发生的地震，在空间上均匀分布，在时间上符合Poisson分布。也有学者[34]假设潜在震源区发生的地震在时间上符合其它类型的分布（如Weibull分布），依据所假设的概率分布，建立估计潜在震源区强震发生率预测模型。

特征地震是指某些断层长期活动过程中，重复发生的多次大地震往往表现出相似的破裂长度、位错分布、和震级大小，有些活动断层在多次地震中表现出局部的相似。如果地震在一个发育比较成熟的断层上发生，并且断层的几何构造、地质背景、物质参数多次地震中未发生很大的改变，那么这些地震很可能就是特征地震。一般认为特征地震模型反应的是单条成熟断层的地震活动性。如果通过古地震学的研究，推断出特征地震的复发周期，即可通过换算得到特征地震的年发生率[32-33]。

地震海啸危险性分析中，需将潜源的地震发生率转换为地震海啸发生率。参考文献（4）中，直接将地震发生率作为地震海啸发生率。参考文献（10）中，假定地震发生在海域的比例（有的潜源包括部分陆地）等于潜源海域部分面积与潜源总面积的比值，将地震发生率与该比值的乘积作为地震海啸发生率。历史地震海啸记录表明，能触发灾害性海啸的地震一般发生在大洋深水区域，并非所有发生于潜源的强震都触发地震海啸。易见，上述两文献中求取地震海啸发生率的方法，会使地震海啸危险性分析结果偏大。可以考虑选定水深指标，以超过该深度的海域面积与潜源总面积的比值与地震发生率的乘积，作为地震海啸发生率，这样也许会使结果更趋合理。

6 耦合潜在地震海啸源参数不确定性效应的随机模拟法

容易看出，地震海啸危险性分析中，潜在地震海啸源位置界定和源参数取值难以避免不确定性。本节在上文所述内容基础上，给出一种可以耦合潜源参数不确定性效应的地震海啸危险性概率分析方法，我们称之为随机模拟法。

首先，完成本文第2节中所述的步骤（1）—（3）。内容包括：（1）依据本文第3节和第4节论述的方法，界定潜源并为潜源断层产状参数赋值。我们建议，根据地震构造、测震资料、震源机制解的分析，估计震中位置、震源深度、断层滑动角这三个参数取值的概率分布；然后采用蒙特卡洛方法，通过随机模拟计算得到震中位置、震源深度、断层滑动角参数的样本值，综合其它潜源参数值，得到潜源参数样本值（需要说明，震级参数或位错参数取值与计算地震海啸发生率的特定震级取值相对应）；（2）选取地震海啸数值模式，以潜源参数样本值作为输入数据，模拟计算海啸波传播；（3）采用本文上节介绍的方法，估算与特定震级相对应的地震海啸发生率。

接下来，完成本文第2节所述的步骤（4），即遴选对场点海啸危险性有贡献的潜源，仍然用场点最大海啸波高超过临界海啸波高为判据。

为了在地震海啸危险性分析中，耦合潜源参数取值不确定性效应，需要改变第2节步骤（5）中的一些作法。

假定一共遴选出M个潜源，l=1,2,...,M。从遴选出的第l个潜源的模拟计算结果中，提取场点最大海啸波高数据，用hmax(r,m,L,W,θ,δ,x0i,y0i,z0i,λi)表示提取出的第i个样本，简记为hmax(i)，用h¯max(r,m,L,W,θ,δ)表示最大海啸波高平均值，简记为h¯max，式中r,m,L,W,θ,δ分别代表场点位置、震级、断层长度、断层宽度、断层走向角、断层面倾角，x0i,y0i,z0i,λi分别代表震中纬度、经度、震源深度、地震断层滑动角的第i个样本。假定样本总数为N,则最大海啸波高平均值为：

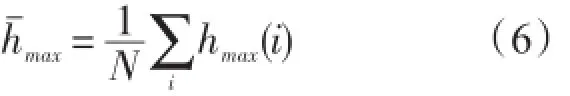
与之相对应的方差为：

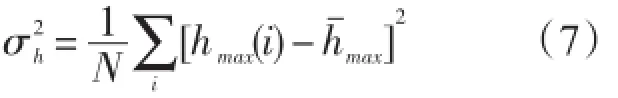
用变量y表示场点最大海啸波高。假定y符合高斯分布，则y的累积分布：

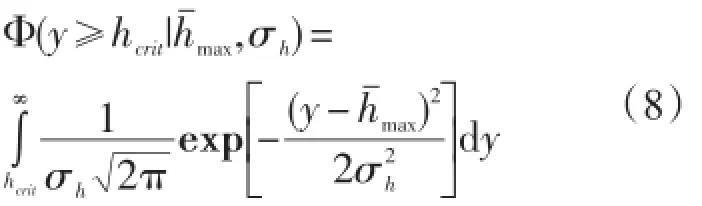
表示第l潜源，当r,m,L,W,θ,δ取确定的值，而x0i,y0i,z0i,λi随机取值时，场点最大海啸波超过海啸临界波高的累积概率。显然场点最大海啸波高y的最大值应该是有限的，记为hmax。如果将区间等分为M段，j=1,2,...,M，取令yj表示第j个区间段中点的值，则（8）式的离散形式为：

用mcrit表示与海啸波高临界值hcrit对应的震级，mmax表示与最大海啸波高最大值对应的震级，nl(r,m)表示第l个潜源震级参数取m时的地震海啸发生率，Nl(r,hcrit)表示第l个潜源的地震海啸发生率，则：

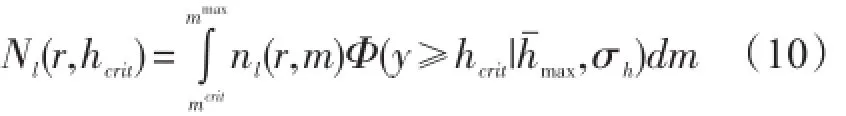
再将震级由mcrit至mmax分为K组，k=1,2,...,K,令Δmk=mk+1-mk，则（10）式的离散形式为：

式（11）可用于计算单源地震海啸发生率。

如前所述，假定一共遴选出M个潜源，l=1,2,...,M。那么，地震海啸总发生率为：

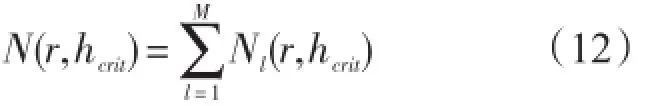
最后，计算场点地震海啸危险性。仍沿用本文第2节步骤（6）中介绍的方法，不再赘述。

7 结语

本文总结了基于数值模拟的地震海啸危险性概率分析的基本步骤;讨论了潜源位置界定原则;论述了潜源参数取值方法和潜源地震海啸发生率估计方法；提出一种基于数值模拟的地震海啸危险性概率分析随机模拟方法。

地震海啸危险性分析中，潜源位置界定，要遵循潜在震源区位置界定的一般原则并参照海域潜在震源位置界定结果，同时要参照震级、震源深度、震中区域海水深度的判据。潜源断层几何参数（断层长度、宽度、走向、倾向角）取值，需要通过板块构造动力学、大地测量学、地震构造、地震活动、海底地貌以及海域地球物理场等方面的综合研究，和历史地震记录、历史海啸记录、海水深度资料的综合分析。分析潜源的地震构造特征、历史地震活动特征以及震源机制解，可以在一定程度上对未来地震的震中位置、震源深度、地震断层滑动方向做出估计。目前地震海啸危险性分析中，潜源位置界定和潜源参数的取值，都难以避免不确定性。

依据本文提出的技术路径和方法，可以实现在地震海啸危险性分析中耦合震中位置、震源深度、地震断层滑动角等潜源参数取值的不确定性效应。

地震海啸危险性概率分析中，潜源参数取值不确定性特征的分析方法，以及这种不确定性对地震海啸危险性分析结果不确定性贡献份额的定量评估方法，是今后需要进一步深入研究的课题。

[1]章在墉,冯时庆.地震危险性分析及其应用[M].上海:同济大学出版社,1996.

[2]Recommendations for Probabilistic Seismic Hazard Analysis: Guidance on Uncertainty and Use of Experts[R].Main Report, 1997.

[3]胡聿贤,鹿林.地震活动性估计的不确定性[M]//地震危险性分析中的综合概率法.北京:地震出版社,1990:176-185.

[4]Geist E L,Parsons T.Probabilistic Analysis of Tsunami Hazards [J].Natural Hazards,2006,37(3):277-314.

[5]Stein S,Geller R J,Liu M.Why earthquake hazard maps often fail and what to do about it[J].Tectonophysics,2012,562-563:1-25.

[6]荆旭.地震危险性分析不确定性表征[J].核安全,2013(1):60-63.

[7]Intergovernmental Oceanographic Commission.Tsunami Glossary [M].Paris,UNESCO.IOC Technical Series,85,2008.

[8]任鲁川,洪明理.地震海啸危险性分析研究进展[J].防灾科技学院学报,2012,14(2):9-14.

[9]温瑞智,任叶飞,李小军,等.我国地震海啸危险性概率分析方法[J].华南地震,2012,31(4):1-13.

[10]Liu Y C,Santos A,Wang S M,et al.Tsunami hazards along Chinese coast from potential earthquakes in South China Sea[J]. Physics of the Earth and Planetary Interiors,2007,163(1-4): 233-244.

[11]Mansinha L,Smylie D E.The Displacement Fields of Inclined Faults[J].Bulletin of the Seismological Society of America, 1971,61(5):1433-1440.

[12]Okada Y.Surface Deformation due to Shear and Tensile Faults in aHalf-Space[J].BulletinoftheSeismologicalSocietyof America,1985,75(4):1135-1154.

[13]Goto C,Ogawa Y,Shuto N,et al.Numerical method of tsunami simulation with the leap frog scheme[Z].IUGG/IOC Time Project.IOC Manual,UNESCO 35.1997.

[14]Titov V V,Gonzalez F I.Implementation and testing of the MethodofSplitting Tsunami(MOST)model[R].NOAA Technical Memorandum ERL PMEL-112,1997.

[15]Titov V,Synolakis C.Numerical modeling of tidal wave runup [J].Journal of Waterway,Port,Coastal,and Ocean Engineering, 1998,124(4):151-171.

[16]Titov V V,Gonzalez F I,Bernard E N,et al.Real-time tsunami forecasting:challenges and solutions[J].Natural Hazards,2005, 35(1):35-41.

[17]Liu P L-E,Woo S-B,Cho Y-S.Computer programs for tsunami propagation and inundation[EB/OL].Cornell University.1998. http://ceeserver.cee.cornell.Edu/pll-group/comcot-down.htm.

[18]Wang W M.User Manual for COMCOT Version 1.7[EB/OL], 2009.http://ceeserver.cee.cornell.edu/pll-group/comcot.htm.

[19]于福江,叶琳,王喜年.1994年发生在台湾海峡的一次地震海啸的数值模拟[J].海洋学报,2001,23(6):32-39.

[20]胡聿贤.地震安全性评价技术教程[M].北京:地震出版社,1999.

[21]胡聿贤.地震危险性分析中的综合概率法[M].北京:地震出版社,1990.

[22]陈颙,陈棋福.印尼地震海啸及其相关的地球物理现象[J].地球物理学进展,2005,20(1):112-117.

[23]Kirby S,Geist E,Lee W H K,et al.Tsunami Source Characterization for Western Pacific Subduction Zones,A Preliminary Report[R].USGS Tsunami Subduction Source Working Group,2005.

[24]Satake K,Tanioka Y.Sources of tsunami and tsunamigenic earthquakes in subduction zones[M]//Seismogenic and Tsunamigenic Processes in Shallow Subduction Zones.Birkhäuser Basel,1999:467-483.

[25]Lee W H K,Kirby S H,Diggles M F.compilers,2010,Program and abstracts of the Second Tsunami Source Workshop[EB/OL]. 2010.

[26]Kirby S H,Wartman J,Choy G L,et al.Large Off-trench EarthquakesandTheirTsunamiPotentials[C]//Programand Abstracts of the Second Tsunami Source Workshop.U.S. Geological Survey Open-File Report 2010-1152,2010.

[27]蒋溥,戴丽思.工程地震学概论[M].北京:世界知识出版社, 1993.

[28]Philip L,Liu F,Wang X M.Andrew John Salisbury.Tsunami Hazard and Forecast Study in South China Sea[EB/OL].http:// ceeserver.cee.cornell.edu/pll-group/comcot.htm.

[29]陈运泰,杨智娴,许力生.海啸、地震海啸与海啸地震[J].物理, 2005,34(12):864-872.

[30]Hanks T C,Kanamori H.A moment magnitude scale[J].Journal of Geophysical Research,1979,84(B5):2348-2350.

[31]Cornell C A.Engineering seismic risk analysis[J].Bulletin of the Seismological Society ofAmerica,1968,58(5):1583-1606.

[32]薛霆虓,邵志刚,傅容珊.特征地震现象和机制分析[J].地球物理学进展,2011,25(6):1887-1896.

[33]Paul Segall.Testing Earthquake Recurrence Models:Space-Time Patterns of Slip-Deficit at Parkfield[EB/OL].http://pangea. stanford.edu/research/CDFM/index.html.

[34]Rikitake T.Probability of a great earthquake to recur in the Tokai district,Japan:reevaluation based on newly-developed paleoseismology,plate tectonics,tsunami study,micro-seismicity and geodetic measurements[J].Earth,Planets and Space,1999,51(3): 147-158.

Principle and method of the seismic tsunami hazard analysis coupling uncertainty effect of potential source parameters

REN Lu-chuan，HUO Zhen-xiang，HONG Ming-li
（Institute of Disaster Prevention,CEA，Hebei 065201 China）

The basic steps of the seismic tsunami hazard analysis based on numerical simulation is summarized. The specification of the potential seismic tsunami source location,selection of potential source parameters as well as estimation of the seismic tsunami occurrence rate is discussed.Meanwhile,a method of seismic tsunami hazard analysis coupling the uncertainty effect of the potential source parameters is proposed in this paper.

seismic tsunamis；hazard analysis；uncertainty；potential source parameters；numerical simulation

P731.25

：A

：1003-0239（2014）06-0007-07

10.11737/j.issn.1003-0239.2014.06.002

2014-03-14

国家自然科学基金项目（41276020）

任鲁川（1958-），男，教授，主要从事自然灾害风险分析、地震灾害和海洋灾害预测研究。E-mail：renluchuan@sina.com