通信中的盲源分离问题及解决方案探讨*
杨 柳,张 杭
(解放军理工大学通信工程学院,江苏南京210007)
通信中的盲源分离问题及解决方案探讨*
杨 柳,张 杭
(解放军理工大学通信工程学院,江苏南京210007)
主要阐述了盲源分离技术应用于无线通信系统时面临的若干问题和解决方案的研究现状。在无线通信系统中,参与混合的源信号是射频通信信号和干扰,这些源信号往往具有循环平稳特性;完成源的混合的无线信道往往受环境影响而发生变化,即具有时变特性;受客观实际条件的限制,观测信号数目往往少于混合源的数目,即表现为欠定混合特性。因此,将盲源分离理论应用于无线通信系统中时,需要特别关注的是循环平稳源、时变、欠定等条件下的盲分离问题。
盲源分离 无线通信 循环平稳 时变混合 欠定混合
0 引 言
随着无线通信技术的发展以及无线设备应用的普及,应用无线环境进行数据通信和信息传输已经成为今后通信网络的主流发展趋势。无线空间中用户数量的增多,频率资源的紧缺,各种通信系统间和系统内部的频率保护间隔的减小,单个信号的多径传输效应,对抗用户间的恶意破坏等等,这些因素的存在都使得无线通信系统遭受干扰的情况越来越普遍,干扰信号的存在降低了无线通信的可靠性,对无线通信系统中传输的信息具有非常大的危害。因此,增强通信系统在干扰环境下的可靠性,是长期的重要研究课题。当前的主要通信抗干扰措施如直接序列扩频技术和跳频技术[1],它们或是通过直接扩展信号传输带宽并配以相关检测实现干扰抑制,或是通过使信号的载波频率在一定的宽频带范围内进行伪随机跳变来躲避干扰,两者均可实现干扰的有效抑制,所获得的容扰容限与带宽的扩展成正比,因此两者是以开销频谱资源为代价来换取抗干扰能力。盲源分离作为一种新兴的盲信号处理技术,能在未知源信号和混合系统参数的条件下,利用多路观测信号恢复相互混叠的各个源信号,这为该技术用于通信系统实现干扰与信号分离奠定了理论基础。利用盲源分离技术实现抗干扰,不需要占用更多的频谱资源,对于频谱资源日益紧缺的今天,这一特性无疑是非常有吸引力的。
将盲源分离技术用于无线通信系统进行抗干扰通信时,下述问题是必须面对的一些关键问题。①传统的盲分离算法往往假设源信号为平稳信号或假设统计量为分段平稳,但是在许多情况下信号的统计特性随时间变化,呈现非平稳特性。例如,无线通信系统中的正弦波已调信号就具有循环平稳性;②目前提出的很多盲分离算法都是在假设信道条件(或混合矩阵)不变或者缓变的条件下提出的,但是对于通信信号的盲分离,由于通信环境的改变、通信终端的运动等因素的影响,盲分离模型中的混合矩阵常常具有时变性;③较为成熟的盲分离技术主要用于解决适定或超定的盲分离问题,即观测信号的数目等于或多于源信号的数目,而实际通信系统中,由于受到设备复杂度等客观条件的限制,接收传感器数量可能会少于源信号数目,导致混合矩阵具有欠定性;④基本的混合模型为瞬时混合,但在通信系统中由于存在传输时延,导致混合具有卷积性。
文中以瞬时混合为前提,分别针对循环平稳源混合、时变混合、欠定混合这些无线通信中所面临的盲分离问题的研究现状进行阐述与探讨。而对于复杂的卷积混合,将在后续工作中进行。
1 盲源分离数学模型
盲源分离问题的处理对象是传感器阵列检测到的信号集,其普适性的模型如图1所示。

图1 盲源分离系统框Fig.1 System block diagram of BSS
其中S(t)=[s1(t),s2(t),…,sN(t)]T,t=0,1,…,T表示N个未知源信号组成的向量;N(t)= [n1(t),n2(t),…,nM(t)]T表示噪声向量;X(t)= [x1(t),x2(t),…,xM(t)]T表示M个传感器阵列接收到的观测信号向量;Y(t)=[y1(t),y2(t),…,yN(t)]T是对源信号的估计向量。
瞬时混合模型输入输出关系如下式所示:

aij(t)表示瞬时混合系统的第j个源到第i个观测信号的冲激响应函数,并且aij(t)是时间t的函数,因此A(t)={aij(t)}表示该混合系统是时变的,即混合矩阵随时间发生变化。
该等式也可用矩阵形式表示:

其中,A是M×N阶的混合矩阵,X=[X(0),X(1),…,X(T)],S与N的定义与X类似。瞬时线性混合信号的分离模型可以表示为:
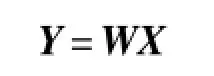
其中,W是N×M的分离矩阵,分离得到的信号Y是对源信号X的一种估计。
观测信号个数M与源信号个数N的大小关系反映了观测信号的信息完备程度,当M≥N时,即超定或适定的情况,此时观测信号是信息完备的;而M<N时,即欠定的情况,此时观测信号是信息不完备的。
2 循环平稳源信号混合盲分离算法
对循环平稳信号进行处理的意义主要表现在两方面:一方面,循环平稳特性反映了信号统计量随时间的变化,这与把信号当作平稳信号处理的方法相比,扩大了分析域,从而获得了分析增益;另一方面,利用信号统计量在时间上的规律性,这与把信号当做非平稳信号处理的方法相比,保留了有用信息,却简化了处理,更易于实时化。
由于通信信号中,大部分信号都为二阶循环平稳信号,即信号的自相关函数为以T0为周期的周期函数,故文中就基于循环平稳信号的二阶统计量研究其盲分离算法。
2.1 基于自然梯度的循环平稳源盲分离算法
自然梯度算法是一种比较经典的盲分离算法,它在随机梯度算法上作了一种改进,且与随机梯度算法相比较,自然梯度算法的收敛速度更快。文献[2-5]提出了基于自然梯度算法的改进盲分离算法。首先,利用信号的二阶循环平稳特性构造代价函数,然后利用自然梯度学习规则最小化该代价函数,突破了传统盲分离算法只处理平稳信号的局限,使得多数具有循环平稳特性的通信信号能够通过这种方法得到有效分离。比较有代表性的文献[6]基于最大似然估计,引入循环自相关代价函数,构建了改进的自然梯度盲分离算法,该算法对循环平稳信号的分离效果和收敛速度明显好于传统的ICA算法。但是,这类算法受到自然梯度算法固有局限性的影响,即迭代步长的选取,已有学者[7]提出了步长自适应的自然梯度循环平稳信号盲分离算法。
2.2 基于空间时频分析的循环平稳源盲分离算法
时频分析(TFA,Time-Frequency Analysis)提供了信号的频谱内容随时间变化的信息,是分析非平稳信号的有力工具。通过考察信号的时频分布,对混叠信号的时频分布矩阵进行联合对角化来实现盲源分离,这种方法能有效分离非平稳信号,并且适用于各种相互独立的(包括高斯)信号,其要求是源信号具有不同的时频分布[8]。比较著名的时频分析工具有短时Fourier变换、小波变换、Cohen类分布(如Wigner-Ville分布)等等。Wigner-Ville分布是一种经典的时频分布,它具有很高的时间和频率分辨率,但是当所分析的信号不是单一成分信号时,会产生交叉项,这些交叉项严重影响了对真实信号的识别。为了改善Wigner-Ville分布,可以采用核函数的方法抑制交叉项的产生[9]。另外,通过采用维纳全时频域搜索来寻找局部最大值的平滑伪Wigner-Ville分布的盲分离算法可以抑制交叉项而且能够保持时频聚集性,并可以达到比传统的ICA更好的分离效果[10],但是,该算法是针对线性瞬时混合模型提出的,对于更为复杂的模型如非线性混合模型和卷积混合模型是否适用则有待于进一步研究。
2.3 基于循环平稳度准则的循环平稳源盲分离算法
循环平稳度(Degree of Cyclostation,DCS)的概念由Gardner[11]于1991年提出,用以度量信号在循环频率α处的循环平稳程度,DCS的值越大表明信号在此循环频率处的循环平稳程度越强。以循环平稳度为准则的盲分离算法,能够很好地抑制混合信号中的噪声,当循环平稳部分是已调信号而平稳部分是复杂噪声时,只需对一路分离信号进行处理即可提取信号,达到抑制噪声的目的,比一般的盲源分离算法简单,而且结果更理想。但该算法的缺点在于,不能同时分离多路循环平稳信号,要想实现循环频率相同的多路源信号的分离,还必须结合使用联合近似对角化算法[12]。
2.4 基于特征值分解的循环平稳源盲分离算法
利用时域范围内的循环平稳信号在频域上的特性,基于特征值分解的盲源分离算法不需要源信号的方差在多个子区间内保持不变,这个条件在很多基于方差循环平稳的分离方法中是必不可少的[13],但该算法仅能应用于小维数源信号混合模型。
3 时变混合盲分离算法
通信系统中,各源的混合是在信道的传输过程中发生的,所以信道的特性体现了混合系统的特性,信道的时变特性即表现了源信号的时变混合。当前对时变问题的研究主要针对时变适定(超定)瞬时混合系统,并采用在线(on-line)的处理方式。在线盲分离算法是一种自适应的算法,自适应处理是指随着数据的不断输入作递归式迭代处理,具有实时处理的特点,因而对时变系统具有一定的跟踪能力。当前的时变盲分离算法主要可以分为以下几类:
3.1 LMS(Least Mean Square)算法
EASI(Equivariant Adaptive Separation via Independence)算法[14]、自然梯度算法(Natural Gradient Algorithm,NGA)[15]、符号自然梯度算法(Sign Natural Gradient Algorithm,S-NGA)[16]以及基于最小互信息的算法[17]都属于典型的在线盲分离算法,这些算法虽然表达形式不同,但都属于LMS型算法。LMS型算法,存在收敛速度与稳态误差间的平衡优化问题,也就是步长参数的优选问题。步长越大,系统的收敛及跟踪速度越快,但同时会导致较大的稳态误差;而步长越小,则稳态误差越小,但是系统的收敛速度较慢,无法对外界环境的变化做出快速反应。因而当这些算法采用固定步长时,迭代过程中就不能兼顾系统对时变系统跟踪能力、算法收敛速度和稳态误差的要求。于是,有学者对算法步长进行优化,提出了变步长(Variant Step-size)盲分离算法:基于分离矩阵权范数[18]的自适应步长盲分离算法、基于峭度[19]的自适应步长盲分离算法、基于自然梯度的两步盲分离算法[20]等,这些算法都具有比固定步长算法更快的收敛速度和更小的稳态误差,其中,前两种算法分别根据信号的分离程度和信号的峭度自适应地调整迭代步长,第三种算法则在自适应步长公式中引入高阶相关系数,综合固定步长和自适应步长算法,进一步提高了算法性能。
3.2 RLS(Recursive Least Square)算法
LMS算法本质上是最速下降算法,其主要优点是计算简单,但因此付出的代价是收敛缓慢,因而,提出了一系列的RLS算法,B.Yang[21]通过引入遗忘因子,建立最小二乘的代价函数,提出了PAST (Projection Approximation Subspace Tracking)算法,该算法是一种RLS类算法,一定程度上提高了算法的收敛性能。在此基础上,X.Zhu和X.Zhang等人[22]首先对观测信号进行白化处理,然后在分离矩阵正交的约束下,提出了基于自然梯度的RLS算法,该算法具有更好的收敛性能和稳定性能。近年, Z.Ding和X.Zhang等人[23]进一步在NPCA(Nonlinear Principal Component Analysis)原则下,提出了基于STF(Strong Tracking Filter)的盲分离算法,该算法的一种特殊形式即为RLS算法,其引入的遗忘因子可利用卡尔曼增益进行自动更新,因而具有更好的时变跟踪性能。简言之,RLS类算法能够提高收敛性能的原因是:其迭代步长不再是经验值,而是根据之前的数据得到的统计意义上的最优值。但此类算法的缺点在于,一是计算复杂,二是对递推计算所引起的累积舍入噪声敏感,会引起算法的不稳定。
3.3 自适应滤波算法
自适应滤波可自动调整其自身参数,使系统性能满足要求,且只需要很少或根本无需任何关于信号和噪声的先验知识。卡尔曼滤波作为一种自适应滤波方法,具有最小均方误差意义下的时变系统跟踪能力,即其参数时变,适用于非平稳随机情况下的滤波且性能优越。张贤达[24]在其文章中提出了利用卡尔曼滤波跟踪混合系统时变的盲分离算法,获得了比基于自然梯度的ICA算法和RLS算法更好的性能,但是,卡尔曼滤波器的收敛性能易受到初始值的影响。N.Das和A.Routray等人[25-26]提出了一种基于H∞范数滤波的盲分离算法,从一定意义上讲,H∞范数滤波是一种带约束的卡尔曼滤波,在时变环境中H∞范数滤波比卡尔曼滤波具有更强的鲁棒性。实验证明,基于H∞范数滤波的盲分离算法比基于卡尔曼滤波的盲分离算法和变步长盲分离算法具有更优越的跟踪时变混合系统的性能。
4 欠定混合盲分离算法
由于在欠定情形下,混合矩阵是不可逆的,因此不能通过经典的独立分量分析等算法进行信号分离;而且即使混合矩阵是已知的,源信号的分离也存在不唯一解。倘若仅利用观测信号,很难精确恢复出源信号,因此,必须利用源信号的一些特性以及先验知识来实现盲源分离。
4.1 基于信号稀疏表示的欠定盲分离算法
信号在满足稀疏性的条件下可得到欠定盲分离的唯一解。所谓稀疏性,直观上说就是信号大部分采样点处取值为零或者接近于零,而少数采样点处远远大于零。当源信号在时域或某个变换域上具有稀疏性并且通过源信号数估计可以得到仅包含一路源信号的信号,即可通过将单源点作为样本估计出混合矩阵,实现信号的分离。目前,国内外的大部分欠定盲分离算法都是利用信号的稀疏性[27]进行的,但这类算法主要用来对由语音、图像等源信号构成的混合信号进行分离;在无线通信系统中,由射频通信信号与干扰这类源构成的混合信号在时频域上无法满足这种稀疏性要求,因而这类方法在解决无线通信系统中的欠定盲分离问题时受到限制。
4.2 基于模型的欠定盲分离算法
基于模型的盲分离算法,适用性强,易于引入先验信息。J.Hirayama和S.Maeda等人[28]提出了一种基于变分贝叶斯的盲分离算法,该算法利用隐马尔可夫模型和比例高斯混合模型对源信号进行建模,在此基础上推导了待估参数的更新公式,从而实现盲分离;S.Sun等人[29]提出了一种VBEM(Variational Bayesian Expectation Maximization)算法,通过建立源信号和混合系统的统计分布模型,针对模型参数设置合理的先验分布引入先验信息,同时实现了混合矩阵和源信号的估计,解决了含噪混合条件下的瞬时混合盲分离问题。虽然,基于模型的盲分离算法并没有讨论混合系统欠定的情形,但是,这些方法也都没有关于系统可逆的假设,亦即有可能通过引入先验信息,解决欠定盲分离问题。
4.3 基于粒子滤波的欠定盲分离算法
粒子滤波是贝叶斯估计基于抽样理论的一种近似算法,它将蒙特卡罗和贝叶斯理论结合在一起,其基本思想是在状态空间中寻找一组随机样本对条件概率密度分布进行近似,以样本均值代替统计均值,从而获得状态的最小方差估计。这种技术适用于任何能用状态空间模型以及传统的卡尔曼滤波表示的非高斯背景的非线性随机系统,精度可以逼近最优估计。不少学者[30-33]将其应用于单通道通信信号的盲分离(是欠定盲分离的一种,即只凭借一路观测信号分离出多路源信号)问题中去,把盲分离问题转化为未知系统参数和信息符号的联合估计问题,并取得了较好的效果。但粒子滤波算法不可避免的缺陷在于其退化问题,需要通过重要性函数的选取、重抽样等方法来改善这一问题。
5 结 语
文中主要针对盲源分离应用于无线通信系统时必须面对的关键问题进行了讨论,分别对循环平稳源问题、时变盲分离和欠定盲分离问题的经典与最新解决方法进行了分析与介绍。
为了将盲源分离技术更好地应用于无线通信系统,还需要对以下问题进行关注:
1)如何有效地利用无线通信信号所呈现出的循环平稳特性,是提高盲源分离算法性能的关键。目前,有一些盲源分离算法利用了信号的二阶循环平稳性,同时许多信号的时变自相关函数中存在着多个周期不可通约的谐波分量,如果能全面的利用这种循环频率,将会很大程度上提高盲源分离算法的性能。此外,通信信号中有些具有非平稳性,因此对一般非平稳信号进行盲源分离将是通信领域的研究重点。
2)目前对时变盲源分离算法的研究鲜有讨论其对通信环境的适应性,例如,算法的收敛性能与信道的多普勒频移、衰落速度等参数之间的关系,因此值得关注。
3)如文中的引言中所述,实际的通信环境中存在传输延迟的情况,此时,观测信号应该是源信号与混合系统冲激响应的卷积,即卷积混合的情形。因而,对时变条件下的卷积混合盲分离算法的研究将具有更大的实际意义。
[1]张邦宁.通信抗干扰技术[M].北京:机械工业出版社,2006:86-87.
ZHANG Bang-ning.Communication Anti-jamming Technology[M].Beijing:China Machine Press,2006:86-87.
[2]何文雪,王林,谢剑英.一种非平稳卷积混合信号的自适应盲分离算法[J].系统仿真学报,2005,17(01): 196-198.
HE Wen-xue,WANG Lin,XIE Jian-ying.An Adaptive Blind Source Separation Algorithm of Non-stationary Convolutive Mixtures[J].Journal of System Simulation, 2005,17(01):196-198.
[3]何文雪,王林,谢剑英.基于自然梯度的非平稳信号自适应盲分离算法[J].上海交通大学学报,2005,39 (04):513-516.
HE Wen-xue,WANG Lin,XIE Jian-ying.An Adaptive Blind Source Separation Approach of Non-stationary Signals by Natural Gradient Rule[J].Journal of Shanghai Jiaotong University,2005,39(04):513-516.
[4]郭彬,张永祥,柯维.一种基于自然梯度的循环平稳信号盲分离算法及其应用[J].船海工程,2011,40(01): 111-114.
GUO Bin,ZANG Yong-xiang,KE Wei.A Blind Source Separation Algorithm and Its Application of Cyclostationary Signals by Natural Gradient Rule[J].Ship and O-cean Engineering,2011,40(01):111-114.
[5]徐洪涛,王跃钢,邓卫强.基于自组织神经网络的非平稳信号盲分离[J].控制与决策,2011,26(05):748-752.
XU Hong-tao,WANG Yue-gang,DENG Wei-qiang. Blind Separation of Non-stationary Sources Based on Self -organizing Neural Network[J].Control and Decision, 2011,26(05):748-752.
[6]郭彬,张永祥,柯维.循环平稳信号的自然梯度盲分离仿真研究[J].震动与冲击,2010,29(S):108-110.
GUO Bin,ZHANG Yong-xiang,KE Wei.Blind Source Separation of Cyclostationary Signals Using An Extended Natural Gradient Method[J].Journal of Vibration and Shock,2010,29(S):108-110.
[7]陈琛.基于自然梯度算法的变歩长盲源分离[D].太原:太原理工大学,2012.
CHEN Chen.Variable Step Size Blind Source Separation Based on Natural Gradient Algorithm[D].Taiyuan: Taiyuan University of Science and Engineering,2012.
[8]BELOUCHRANI A,AMIN M G.Blind Source Separation Based on Time Frequency Signal Representations[J]. IEEE Transactions on Signal Processing,1998,46(19): 2888-2897.
[9]马明,沈越泓,牛英涛.基于空间时频分布的非平稳信号盲分离算法性能研究[J].探测与控制学报,2007, 29(30):56-60.
MA Ming,SHEN Yue-hong,NIU Ying-tao.Performance of Blind Source Separation based on Spatial Time-frequency Distribution for Non-stationary Signals[J].Journal of Detection and Control,2007,29(30):56-60.
[10]石和平,曹继华,刘霄.基于时频分布的非平稳信号盲分离算法[J].计算机应用,2011,31(02):181-183.
SHI He-ping,CAO Ji-hua,LIU Xiao.Blind Source Separation for Non-stationary Signal based on Time-frequency Analysis[J].Journal of Computer Applications, 2011,31(02):181-183.
[11]ZIVANOVIC GORAN D.,GARDNER WILLIAM A.. Degrees of Cyclostationarity and Their Application to Signal Detection and Estimation[J].Signal Processing, 1991,22(02):287-297.
[12]张海燕.基于循环平稳度和联合近似对角化的盲源分离算法研究[D].太原:太原理工大学,2011.
ZHANG Hai-yan.Blind Source Separation Algorithms based on Degree of Cyclostationary and Joint Approximate Diagonalization[D].Taiyuan:Taiyuan University of Science and Engineering,2011.
[13]邱意敏,周力.基于特征值分解的循环平稳离散时间信号的盲分离[J].计算机应用研究,2012,29(11): 4117-4120. QIU Yi-min,ZHOU Li.Eigenvalue Decomposition Based Blind Separation for Cyclo-stationary Discretetime Signals[J].Application Research of Computers, 2012,29(11):4117-4120.
[14]CARDOSO J F,LAHELD B H.Equivariant Adaptive Source Separation[J].IEEE Transactions on Signal Processing,1996,44(12):3017-3030.
[15]AMARI S.Natural Gradient Works Efficiently in Learning [J].Neural Computation,1998,21(10):251-276.
[16]YUAN L,WANG W,CHAMBERS J A.Variable Stepsize Sign Natural Gradient Algorithm for Sequential Blind Source Separation[J].IEEE Signal Processing Letters,2005,10(12):589-592.
[17]HILD KENNETH E,ERDOGMUS D,PRINCIPE JOSE C.Blind Source Separation of Time-varying Instantaneous Mixtures Using an on-line Algorithm[C]//IEEE Intel.Conf.on Acoustics,Speech and Signal Proc.. USA:IEEE Piscataway NJ,2002:993-996.
[18]李广彪,张剑云.基于分离矩阵的步长自适应EASI算法[J].舰船科学技术,2006,28(05):69-72. LI Guang-biao,ZHANG Jian-yun.Adaptive Step-size EASI Algorithm based on Separating Matrix[J].Ship Science and Technology,2006,28(05):69-72.
[19]付卫红,史凡,刘乃安.适用于时变信道环境的盲源分离算法[J].电子科技大学学报,2012,41(04):512-515. FU Wei-hong,SHI Fan,LIU Nai-an.Blind Source Separation Algorithm for Time Varying Channel[J]. Journal of University of Electronic Science and Technology of China,2012,41(04):512-515.
[20]李思怡,王永威.一种基于自然梯度的两步盲源分离算法[J].微电子学与计算机,2013,30(06):169-172. LI Si-yi,WANG Yong-wei.Blind Source Separation based on Two-Segment Natural Gradient Algorithm[J]. Microelectronics and Computer,2013,30(06):169-172.
[21]YANG B.Projection Approximation Subspace Tracking [J].IEEE Transactions on Signal Processing,1995,43 (01):95-107.
[22]ZHU X,ZHANG X.Adaptive RLS Algorithm for Blind Source Separation Using a Natural Gradient[J].IEEE Signal Processing Letters,2002,9(12):432-435.
[23]DING Z,ZHANG X,ZHU X.Nonlinear Principal Component Analysis Using Strong Tracking Filter[J].Tsinghua Science and Technology,2007,12(06):652-657.
[24]LV Q,ZHANG X,JIA Y.Kalman Filtering Algorithm for Blind Source Separation[C]//Inter.Conf.on A-coustics,Speech,and Signal Processing.USA:IEEE Piscataway NJ,2005:257-260.
[25]DAS N,ROUTRAY A,DASH P K.A Robust H∞ Learning Approach to Blind Separation of Slowly Timevarying Mixture of Acoustic Electromechanical Signals [J].Mechanical Systems and Signal Processing, 2009,6(23):2049-2058.
[26]DAS N,ROUTRAY A,DASH P K.A Robust H∞Learning Approach to Blind Separation of Signals[J]. Digital Signal Processing,2010,20(09):410-416.
[27]毛欣,徐慨,刘杰.盲信号分离技术现状与发展动态[J].通信技术,2013,46(08):24-26. MAO Xin,XU Kai,LIU Jie.Present Situation and Development of Blind Signal Separation Technology[J]. Communicatons Technology,2013,46(08):24-26.
[28]HIRAYAMA J,MAEDA S,ISHII S.Bayesian Noisy ICA for Source Switching Environments[C]//IEEE/SP 13th Workshop on Statistical Signal Processing.USA: IEEE Piscataway NJ,2005:1031-1036.
[29]SUN S,PENG C,HOU W,et al.Signal Blind Source Separation Based on Time Series Variational Bayesians theory [J].Digital Signal Processing,2009,30(08):1571-1576.
[30]LIU KAI,LI HUI,DAI X,et al.Single Channel Blind Signal Separation of Cofrequency MPSK Signals[J]. Journal of Information and Computation Science,2005, 2(02):283-287.
[31]TU S,CHEN S,ZHENG H,et al.Particle Filtering Based Single-channel Blind Separation of Co-frequency MPSK Signals[C]//Inter.Symposium on Intelligent Signal Proc.and Communications Systems.USA:Institute of Electrical and Electronics Engineers Inc.Piscataway NJ,2008:582-585.
[32]刘凯.粒子滤波在单通道信号分离中的应用研究[D].合肥:中国科学技术大学博士学位论文,2007. LIU Kai.The Application of Particle Filter in Single Channel Signal Separation[D].Hefei:Doctoral Dissertation of University of Science and Technology of China,2007.
[33]李响.基于粒子滤波的单通道盲分离算法研究[D].郑州:郑州大学,2012. LI Xiang.The Research of Single Channel Blind Source Separation Algorithm Based on Particle Filter[D]. Zhengzhou:Zhengzhou University,2012.

杨 柳(1989—),女,硕士研究生,主要研究方向为盲信号处理;
YANG Liu(1989-),female,graduate student,majoring in blind signal processing.
张 杭(1962—),女,教授,博士生导师,主要研究方向为盲信号处理,通信抗干扰等。
ZHANG Hang(1962-),female,professor,doctoral tutor,mainly engaged in blind signal processing, communication anti-jamming etc.
Discussion of Blind Source Separation Problem and Its Solution in Communication
YANG Liu,ZHANG Hang
(Institute of Communication Engineering,PLA University of Science and Technology, Nanjing Jiangsu 210007,China)
This paper mainly describes the problems and its solutions of blind source separation(BSS)in wireless communication system.In wireless communication system,the source signals are radio frequency signals or interference signals with cyclostationarity;meanwhile,the wireless channel where the sources are mixed is easily influenced by the environment,as a result,it is time-varying;in addition,restricted by the objective conditions,the number of observation signal is often less than the source signal,which is called underdetermined.Consequently,in wireless communication system much attention should be paid to BSS problems under the cyclostationarity and time-varying and underdetermined conditions.
BSS(blind source separation);wireless communication;cyclostationarity;time-varying mixing;underdetermined mixing
TN92
A
1002-0802(2014)01-0001-06
10.3969/j.issn.1002-0802.2014.01.001
国家自然科学基金项目:欠定条件下基于扰信分离的信干比增强方法研究(No.61001106)
Foundation Item:A Signal-to-jamming Ratio Enhancement Research based on the Separation of Interference and Signal in the Underdetermined Condition(No.61001106)

