Long-rod penetration:the transition zone between rigid and hydrodynamic penetration modes

Jian-feng LOU*,Yan-geng ZHANG,Zheng WANG,Tao HONG,Xiao-li ZHANG,Shu-dao ZHANG

Institute of Applied Physics and Computational Mathematics,Beijing 100094,China

1.Introduction

Long-rod penetration in a wide range of velocity means that the initial impact velocity varies in a range from tens of meters per second to several kilometers per second.Forrestal[1,2]conducted the penetration experiments with spherical-nose or ogive-nose steel projectiles and 6061-T6511 aluminum targets at striking velocities between 0.5 km/s and 3.0 km/s.Wickert[3]performed the experiments with tungsten penetrator and aluminum alloy target in the velocity range from 0.25 km/s to 1.9 km/s.These experiments indicate that there are three response regions for long-rod penetration in a wide range of velocity,it is found that there are three response regions as shown in Fig.1.

(I)In low-speed range,the long rod projectile maintains rigid state,and the penetration depth increases with striking velocity.

(II)In medium-speed range,the nose of rod deforms and even is blunted,and then the penetration depth decreases.It will suddenly draw down if erosion or fracture happens.

(III)In high-speed range,the nose erodes and fails to lead to the consumption of long projectile due to instantaneous high pressure.If striking velocity keeps on increase,the penetration depth will increase again,and tend to reach a steady value finally.

Fig.1.Three response regions for penetration in a wide range of velocity.(a)The response regions of steel rods penetrating aluminum targets[1].(b)The response regions of tungsten penetrators penetrating aluminum targets[3].

So far,the theoretical study has focused on the first and the third response regions.There has been little known about the second response region due to the complexity of this problem.The transition zone was discussed in Refs.[4]and[5],but it was simplified as a strong discontinuity,which means that the penetration depth is assumed to decline suddenly when the impact velocity exceeds a critical velocity.For most numerical simulation studies,the same material model was used throughout the entire velocity range[6,7],or it was simplified into two response zones[8].Lan tried to use a unified model to discuss this issue[9],however,the result is far from been satisfied.

In this paper,we put forward the idea of dividing the velocity range into three regions and building independent theoretical model for each region to address this issue.Herein,the first problem is how to determine the limits of each region.According to the experimental results from Forrestal et al.[11]and Wickert[3],the penetration mechanism is rigid penetration in the first region and erosion penetration in the third region.Thus,to better analyze this problem,two velocities,Vrand Vth,are defined.Vris critical rigid velocity,below which the projectile remains rigid penetration;Vthrepresents critical erosion velocity,above which erosion occurs.Accordingly,the entire velocity range can be divided into three regions,and the second region with the boundary velocities(Vrand Vth)is the transition zone.

Another major problem is how to build the theoretical model for each region.For the velocities within low-velocity range(V0≤Vr)and high-velocity range(V0＞Vth),a lot of analytic models,as reviewed in Ref.[10],have been proposed.Here,the appropriate models are chosen for these two regions by comparing the characteristics and applicability of these models.The model proposed in Ref.[11]is used to calculate the depth of rigid penetration in low-velocity region.A comparative analysis of the popular high-velocity penetration models was presented in Ref.[15].One of them is the Tate model[12-14],in which the target resistance is set to be constant.Another one is Anderson-Walker model[16],in which the target resistance varies with penetrating velocity,making it more close to real situation.Thus,the Anderson-Walker model is chosen to calculate the penetration depth of the third region.

The difficulty of this work is to construct an appropriate theoretical model for the second region(transition zone).This is due to the complicated penetration mechanism in this region involving large plastic deformation in projectile head leading to the reduction of its length,blunted head resulting in the increase of target resistance and the weakening of penetration capability.If erosion happens,the penetration depth will decline sharply,almost halved.What's more,it is a relatively narrow velocity range,almost 100 m/s-200 m/s,in which penetrator head changes easily from large deformation to erosion.As shown in Ref.[1],such velocity range is 892 m/s-1042 m/s,967 m/s-1037 m/s and 1086 m/s-1174 m/s for the average Rockwell hardness Rcof 36.6,39.5,and 46.2,respectively,in the experiments of spherical nosed steel rods impacting the aluminum targets.In the case of penetration by tungsten projectiles[3],the velocity range is 695 m/s-785 m/s.In this paper,a phenomenological model to calculate the penetration depth in the transition zone is constructed based on the analysis of penetration behavior in the transition zone.

2.Method to determine boundary velocity of transition zone

2.1.Critical rigid velocity Vr

To achieve the critical rigid velocity Vrat which the projectile changing from rigid to deforming rod,it is necessary to know the stresses acting on the rod/target interface at the threshold velocity.On the side of rod the stress is the effective strength Yeff,and on the side of target it is resistance to penetration H.

During the early stages of penetration,the rod nose experiences a transient lateral stress Hlat,which resists the process of crater formation due to the target strength.Once the rod is embedded in the target,the lateral stress like an effective lateral support prevents the rod nose from deforming and eroding.The direct consequence of this support is to increase the strength of the rod from Ypto an effective strength Yeff,with the Tresca yield condition,Yeff=Yp+Hlat,as was done by Segletes[5].Because the lateral stress is closely related to the pressure needed to open a cavity in the target,the value of Hlatat the threshold velocity can be assumed to be equal to the minimal pressure Pcneeded to open the cavity.Bishop et al.[17]and Hill[18]presented the method to analyze the value of Pcin the cavity-expansion analysis model,while Rosenberg[19]studied the critical(minimal)pressure by simulation.The values of Pcmeasured by different methods were very close,about 3 times of target strength,Pc≈3Yt.When impact velocity equals Vr,the effective strength of long rod Yeffis

Many research results show that the target resistance H,which the rod experiences as it penetrates the target,increases gradually from the initial value H0to the steady value Rtduring the entrance phase.The initial resisting stress can be obtained from static indentation analysis,as was done by Wijk[20],and the value of H0is about 2.8Yt-3Yt.It sustains almost tens of microseconds for the resisting stress H increasing from H0to Rt,the depth of penetration for the early stages is about six times the rod diameter[21].However,there is no way to account for the accurate change in H with time,so the average of the two values is taken to represent the axial stress on the rod nose.

As the impact speed equals the threshold velocity Vr,the stagnation pressure on the target side is 1/2ρt.So it turns out by equating the stresses on both sides of the rod/target interface,

Substituting Eqs.(1)and(2)into Eq.(3),the critical rigid velocity can be obtained,

2.2.Critical erosion velocity Vth

As the impact speed equals the threshold velocity Vth,the erosion occurs on the nose of rod,even fracture,and then the depth of penetration decreases sharply.

A possible reason for the erosion during the rod penetration at high speed is that the rod erosion rate exceeds the rate of gross plastic deformation or plastic wave speed[22].It has been shown by Billington et al.[23,24]that a dynamic stress-strain curve of metals has two linear regions.One is elastic deformation,and the other is plastic deformation.The propagation speed of gross plastic deformation associated with high stress is governed by the tangent modulus in the second linear region of the stress-strain curve,and is usually between 1/3 and 1/10 of the elastic wave speed.Let the limiting dynamic tangent modulus associated with the plastic fl ow of the rod material be denoted by Eap,and let the speed of propagation of gross plastic distortion be denoted by w,we have

where Eapis tangent modulus,andρpis the density of rod.

An estimate of the rod erosion rate w(w=v-u)can be determined from the modified Bernoulli equation in Ref.[12].Substituting u=v-w into Bernoulli equation,and setting w=,the hydrodynamic velocity(Vth)may be obtained,

Then the hydrodynamic velocity can be directly used as critical erosion velocity.

3.Phenomenological model of target resistance and formula of penetration depth calculation

Rosenberg and Dekel[21]simulated the deformation of steel rod nose with the change of impact velocity in the transition zone.The simulation results indicate that the deformations of the rods are very small as long as the impact velocity is below the corresponding threshold velocity.While exceeding the threshold value,their deformations increase sharply.This explains the steep reduction of penetration depth in a certain extent.

For penetration problem of a deforming non-erosive penetrator in the transition zone,a dimensionless parameter,Ks=A/A0,for cross-sectional area is defined in order to construct an analytical model.Here,A0is the initial crosssectional area of long rods,and A is the cross-sectional area of deforming rod.

According to the simulation results of 1.6 GPa rod in Ref.[21],the dimensionless parameter for cross-sectional area,Ks,at different impact velocity can be calculated,seeing the black squares in Fig.2.If the data is nonlinearly fit,the relationship between the dimensionless parameter and impact velocity can be obtained from Eq.(7)and the red line in Fig.2.

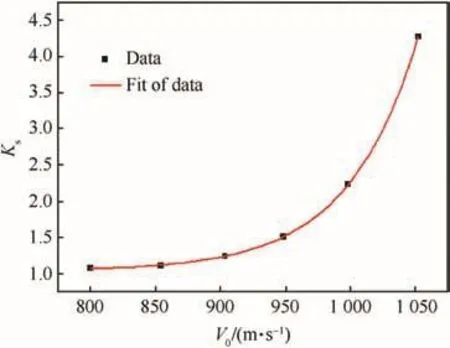
Fig.2.Dimensionless parameter for cross-sectional area as a function of impact velocity.

Hereby,for arbitrary case,in order to analyze the relationship between the dimensionless parameter for crosssectional area of rod nose and impact velocity,an exponential equation can be postulated,as Eq.(8),

where C1and C2are undetermined coefficients,which are only related to the boundary conditions by postulation.If the boundary conditions of transition zone are known,that is,the dimensionless parameters for impact velocity Vrand Vthare obtained,marked as Ks1and Ks2,respectively,then,

so that the coefficients can be obtained

Substituting Eq.(10)into Eq.(8),the relationship between the dimensionless parameter for cross-sectional area and impact velocity is obtained.

The experimental data in Ref.[1]and the simulation results in Ref.[21]show that,as the deforming non-erosive rod is changed to erosive penetrator,the diameter of rod nose is about 1.4-1.6 times the original diameter, so Ks2=1.96～2.56.As the impact velocity equals Vr,the deformation of rod nose is very small,so Ks1can be taken as 1.01.

According to the results in Ref.[21],the deformation of rod nose mainly happens for a very short time in the initial stage.Therefore,it can be assumed that the rod nose deforms and the cross-sectional area increases at the instant of impact in the transition zone(Vr≤V0＜Vth),the rod continues penetrating as a rigid body,and it won't deform anymore in following time.

Since the target resistance for projectile is related with the cross-sectional area of rod,the target resistance Rtfor undeformed rod can be multiplied by dimensionless parameter Ksfor cross-sectional area,that is KsRt.The value is used as the target resistance Rtfor deforming non-erosive rod.

A phenomenological model of target resistance,related with the boundary velocity,in the transition zone can be obtained.

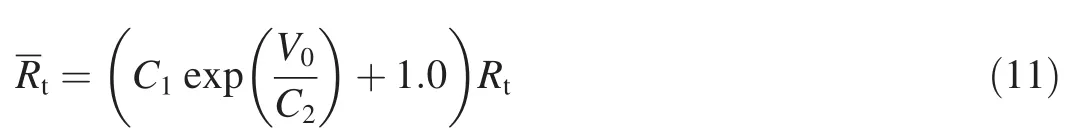
The undetermined coefficients C1and C2can be calculated using Eq.(10).

If the effective length of penetrator is Leffin the transition zone,the formula of penetration depth calculation can be obtained by replacing AYtin Forrestal's model[11]with KsRt.

Table 1Main parameters of rods and targets.

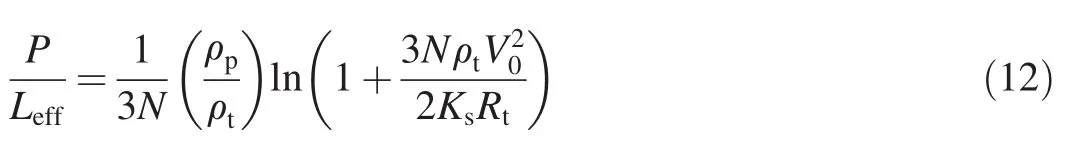
where Ksis determined by Eq.(8),and N is 0.5 as the nose shape is assumed to be hemispherical.

4.Sectional theoretical analysis model for penetration in a wide range of velocity

For the issue of penetration in a wide range of velocity,a theoretical analysis model combined by three sections is presented.In the transition zone,the modified formula(Eq.(12))for penetration is used.For the cases of low-speed range(V0≤Vr)and high-speed range(V0＞Vth),the appropriate models are chosen for rigid projectile penetration and for rod high-speed penetration.The theoretical analysis model is combined by following sections,

(1)In low-speed range V0≤Vr,the model in Ref.[11]is used to calculate the depth of rigid penetration.

(2)In transition zone Vr≤V0＜Vth,the phenomenological model(Eq.(11))of target resistance related to boundary velocities is used to solve the resisting stress of deforming non-erosion penetrator,and the modified formula(Eq.(12))is used to calculate the penetration depth.

(3)In high-speed range V0＞Vth,Anderson-Walker model[16]is used to solve the penetration depth of erosion rod.

The new theoretical analysis model was used to calculate the experiments given in Ref.[1]and Ref.[3].The main parameters of rods and targets are listed in Table 1,Ks1=1.01,Ks2=1.96.The boundary velocities of transition zone were estimated by Eqs.(4)and(6),and the comparison with the experimental results is shown in Table 2.The calculated results are in good agreement with the experimental results,which shows the rationality and correctness of the theoretical formula.

For the experiments of tungsten rods penetrating aluminum targets in Ref.[3],the experimental data and calculated resultsobtained by the new model and Tate's model are shown in Fig.3(a).In Fig.3,vertical coordinate expresses dimensionless depth of penetration.The discrepancy between the calculated results by the new model and the experimental data is verys mall over the wide velocity range.In high-speed range,Anderson-Walker model[16]is used,in which the target resistance decreases as the penetrating velocity increases,the actual situation is more in line with the physical problems so that the calculated values agree well with the experimental results.While target resistance is constant in Tate's model,the calculated results are smaller,and the deviation from experimental results is greater with the increase in speed.of velocity.This model is composed of three parts:In lows peed range(V0≤Vr),the model in Ref.[11]is used to calculate the depth of rigid penetration;in transition zone(Vr≤V0＜Vth),a modified formula[Eq.(12)]is used;and in high-speed range(V0＞Vth),the Anderson-Walker model(1995)is used.The penetration depth predicted by this combined model is in good agreement with the experimental data.

Table 2Comparison of calculated and experimental results of boundary velocity of transition zone.

The key point in this paper is that an appropriate method is built to solve the penetration depth of transition zone.Based on the experimental data and simulation results,the boundary condition of the transition zone was determined.The relationship between the cross-sectional area of rod nose and the

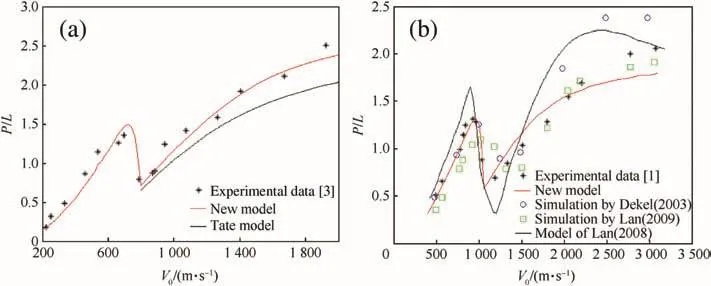
Fig.3.Comparison of calculated results from different methods and experimental data.(a)Calc.and Exp.results of tungsten rods penetrating aluminum targets.(b)Calc.and Exp.results of steel rods penetrating aluminum targets.

The penetration experiments were conducted on steel(Rc=39.5)projectiles with spherical-nose and aluminum(6061-T6511)targets in Ref.[1],which were simulated by Rosenberg and Dekel[7],Lan and Wen[6,9].Together with the results calculated by our new analysis model,all results are indicated in Fig.3(b).Blue hollow circles express the simulation results in Ref.[7],in which the failure criterion was considered.The failure strains of rod and target are 0.5 and 0.6,respectively.There is a great difference between the simulation and experimental data in the high-speed range(V0≥2000 m/s).Green hollow squares express the simulation results in Ref.[6],which differ largely from the experimental values in low-speed range(V0＜1200 m/s).While the calculated values by the analysis model in Ref.[9](black line)are greater than the experimental data almost in the whole velocity range,especially in the velocity range of 1600 m/s-2700 m/s,the calculated values deviate largely from the experimental data.The red line in Fig.3 expresses the results calculated by our new combined theoretical model,which has a good agreement with the experimental data in the whole velocity range,and describes the characteristics of three response regions.

5.Conclusions

A new combined theoretical analysis model was proposed for the long-rod penetration into metal target in a wide range impact velocity was also obtained,suggesting that the dimensionless cross-sectional area changes exponentially with the impact velocity.A phenomenological model to describe the target resistance for transition zone relating to boundary condition was built,and a formula to calculate the penetration depth was derived.

Acknowledgements

This work is supported by the National Natural Science Foundation of China(No.11302031,11371069,11372053).

[1]Forrestal MJ,Piekutowski AJ.Penetration experiments with 6061-T6511 aluminum targets and spherical-nose steel projectiles at striking velocities between 0.5 and 3 km/s.Int J Impact Eng 2000;24(1):57-67.

[2]Piekutowski AJ,Forrestal MJ,Poormon KL,Warren TL.Penetration of 6061-T6511 aluminum targets by ogive-nose steel projectiles with striking velocities between 0.5 and 3.0 km/s.Int J Impact Eng 1999;23(1):723-34.

[3]Wickert M.Penetration data for a medium caliber tungsten sinter alloy penetrator into aluminum alloy 7020 in the velocity regime from 250 m/s to 1900 m/s.In:Proc 23rd int symp ballistics;2007.pp.1437-44.Tarragona,Spain.

[4]Chen XW,Li QM.Transition from non-deformable projectile penetration to semi-hydrodynamic penetration. ASCE J Eng Mech 2004;130(1):123-7.

[5]Segletes SB.The erosion transition of tungsten-alloy long rods into aluminum targets.Int J Solids Struct 2007;44(7-8):2168-91.

[6]Lan B,Wen HM.Numerical simulation of the penetration of a sphericalnosed 4340 steel long rod into semi-infinite 6061-T6511 aluminum targets.Eng Mech 2009;26(10):183-90.

[7]Rosenberg Z,Dekel E.Numerical study of the transition from rigid to eroding-rod penetration.J Phys IV Fr 2003;110:681-6.

[8]Lou JF,Wang Z,Hong T,Zhu JS.Numerical study on penetration of semi-infinite aluminum-alloy targets by tungsten-alloy rod.Chin J High Pres Phys 2009;23(1):65-70.

[9]Lan B.A combined numerical and theoretical study of long rod penetration into semi-infinite targets.Ph.D.thesis.Hefei:University of Science and Technology of China;2008.p.5.

[10]Lou JF.Theoretical model and numerical study on penetrating into semiinfinite targets.Ph.D.thesis.Mianyang:Chinese Academy of Engineering Physics;2012.p.5.

[11]Forrestal MJ,Warren TL.Penetration equations for ogive-nose rods into aluminum targets.Int J Impact Eng 2008;35(8):727-30.

[12]Tate A.A theory for the deceleration of long rods after impact.J Mech Phys Solids 1967;15(6):387-99.

[13]Tate A.Further results in the theory of long rods penetration.J Mech Phys Solids 1969;17(3):141-50.

[14]Alekseevskii VP.Penetration of a rod into a target at high velocity.Comb Expl Shock Wave 1966;2(2):3-66.

[15]Lou JF,Hong T,Wang Z.Theoretical models of high-speed long rods penetrating into semi-infinite targets and analysis of influencing factors.Chinese nationaldefence science and technology report,GFA0164368G;2013.

[16]Walker JD,Anderson CE.A time-dependent model for long-rod penetration.Int J Impact Eng 1995;16(1):19-48.

[17]Bishop RF,Hill R,Mott NF.The theory of indentation and hardness.Proc R Soc 1945;57(3):147-59.

[18]Hill R.The mathematical theory of plasticity.London:Oxford University Press;1950.

[19]Rosenberg Z,Dekel E.A numerical study of the cavity expansion process and its application to long-rod penetration mechanics.Int J Impact Eng 2008;35(3):147-54.

[20]Wijk AG.High-velocity projectile penetration into thick armor plates.Int J Impact Eng 1999;22(1):45.

[21]Rosenberg Z,Dekel E.On the deep penetration of deforming long rods.Int J Solids Struct 2010;47(2):238-50.

[22]Tate A.A possible explanation for the hydrodynamic transition in high speed impact.Int J Mech Sci 1977;19(2):121-3.

[23]Billington EW,Brissenden C.Dynamic stress-strain curves for various plastics and fibre-reinforced plastics.J Phys D 1971;32(4):272-86.

[24]Billington EW,Tate A.The mechanical properties of copper zinc and aluminium tested in compression. Proc R Soc Lond A 1972;327(1568):23-46.