Problem of the reference height of the projectile trajectory as a reduced meteo-ballistic weighting factor

Vladimir CECH*,Ludek JEDLICKA,Jiri JEVICKY

aOprox,Inc.,Kulkova 8,Brno 615 00,Czech Republic

bDepartment of Weapons and Ammunition,University of Defence,Kounicova 65,Brno 662 10,Czech Republic

cDepartment of Mathematics and Physics,University of Defence,Kounicova 65,Brno 662 10,Czech Republic

1.Introduction

It follows from the analysis of the artillery fire errors,e.g.Refs.[1,2],that approximately two thirds of inaccuracy of the indirect artillery fire is caused by inaccuracies in determination of met parameters included into the meteorological error budget[1].Consequently,it is important always to pay close attention to the problems of inclusion of the actual met parameters into ballistic calculations.

The following met parameters are primarily utilized in the ballistics:wind w(and its components:range wind wx,cross wind wz),air pressure p,virtual temperature τ,and air density ρ.Due to practical reasons these parameters will be marked as met parameters(elements)μ.In the ballistics,it is also necessary to know at least the variation of met parameters with the height y above the gun muzzle level μ= μ(y).Each met parameter is characterized by its standard course with the geopotential height hG,i.e.μSTD(hG).More detailed information on standard atmospheres can be found e.g.in Refs.[2,3].

During the last 40 years the effect of current non-standard met conditions can be used directly for the calculation of aiming angles even in the field conditions.Corresponding met parameters are provided in the form of standardized met messages,e.g.METGM[4]or METCMQ[5].Also a number of projectile trajectory models can be used for the ballistic calculations,e.g.modified point mass trajectory model described in Refs.[6,7](See Table 1).

But at the same time the methods based on the use of the tabular firing tables are still utilized for the calculation of aiming angles[8,9]in practice.Their utilization assumes determination of ballistic elements μB(ballistic wind wB,wxB,wZB,ballistic(virtual)temperature τB,ballistic density ρB;ballistic pressure pB;pBis not commonly used in practice),e.g.Refs.[2,9-11].Required met data are again provided in the standardized met messages METBKQ[12],METEO-11 or METEO-44[2,9,13,14].

Table 1List of notation.

The weighting factors(WF)q(μ)(wind q(w),temperature q(τ)and density q(ρ)weighting factors)are used for calculation of ballistic elements μB.The weighting factors q(μ)incorporate characteristics of weapon and ammunition into the calculations.Their magnitude is published e.g.in Ref.[12].

Use of the weighting factors q(μ)follows from the linearized solution of projectile trajectories for non-standard trajectories that are close to standard ones.For example the perturbation methods described in Ref.[11]can be utilized for these purposes.The first step is always the calculation of the corresponding weighting(factor)function(WFF)r(μ).The weighting factors q(μ)are derived consequently from the calculated WFF.Methods of calculation of the WFF were gradually developed in the past,see e.g.Refs.[10,11].The most widespread method is that proposed by Garnier,M.(before 1920)and later modified by Bliss,G.A.(before 1920).The method of calculation of the WFF that is used further in the article is another modification of the Garnier-Bliss method,e.g.Refs.[2,9,15,16].

When using the met message METEO-11 or 44,the weighting factors q(μ)are proportional only to the relative height of individual zones-layers.The effect of ballistic parameters of weapon and munition is included into calculations by use of the reference height of trajectory(RHT,YR)that is a multiple of the trajectory vertex height(TVH,YS),i.e.YR=KR·YS,KR=sYR=approx.0.8-1.4.The magnitudes of RHT and TVH are presented in the tabular firing tables for each combination of projectile and charge as a function of the range of fire X.The RHTs are calculated from the corresponding WFF.

When using the met message METBKQ[12],the ballistic parameters μBare found using the TVH YScorresponding to the given range of fire X.On the other hand in the met message METEO-11 or-44 the ballistic parameters μBare found with the use of RHT YRthat also corresponds to the given range of fire X.

From the authors' point of view there are three reasons to deal with the issue of WFF and the consequently derived WF and RHT.

The first reason has already been clarified.Without the introduction of WFFs and derived WFs and RHTs it is not possible to calculate ballistic elements μBand to create and use the tabular firing tables.

The second reason is the fact that the study of the issue of WFF is the most effective way for understanding the mechanisms in which the met parameters μ affect the shape of the projectile trajectories.

The third reason is specifically for countries utilizing at the same time the tabular firing tables in format described in Ref.[8]together with the standardized met message METBKQ[12]and firing tables that were created in former USSR and its satellites since the late 1950s.Their utilization is based on the introduction of the RHT and use of the standardized met message METEO-11 or-44.The crucial point is the study of possibilities of mutual conversions of WFF,WF,and RHT and also the creation of a methodology for the mutual evaluation of accuracy of both the previously mentioned approaches.

The problems connected with the calculation of WFF are only of numerical nature[15,16].Ambiguities and inaccuracies appear after calculation of the WFF during calculation of RHT.Ambiguities are due to the fact that the original material describing the method of calculation of RHT is not generally available(according to Ref.[16]it is USSR origin,probably from 1956).As an example of existing issues that can be mentioned the case when RHT YR＞TVH YS(KR＞1)and the principle of causality is violated because,in the calculation of the RHT,parameters of atmosphere layers through which projectile never travelled are used.This fact is not discussed in available literature at all.

Comparison of all available information and the use of numerical simulations led to clarification of the entire issue and also led to its interconnection with the methods of WFs determination.

The main aim of this paper is to clarify the problem of causality violation and conduct an analysis of methods of the RHT calculations because the available literature,as stated above,contains a number of inaccuracies and ambiguities.It will be shown that for each weight system WF can be found a unique RHT but,on the other hand,for a given RHT there are more than one weight systems WF.The magnitudes presented in the METBKQ[12]for the type of message:surface-to surface fire(K=3)will be used as an illustrative example.Unfortunately the extent of this article does not allow the authors to present a detailed analysis of the accuracy of indirect fire prepared in accordance with previously mentioned methods,e.g.with use of the methodology described in Ref.[1]or[13].

2.Historical background

The extensive use of computers in the last 40 years allows a fast integration of the equations describing projectile trajectories in both standard and non-standard conditions,e.g.Refs.[6,7].The analyses based on the use of numerical calculations are usually carried in such a way that a number of variants of parameter changes affecting the projectile trajectory are chosen and corresponding changes of projectile trajectory parameters are calculated,e.g.changes in range,time of flight,deflection,etc.Calculated trajectory parameters changes are consequently analysed with the aim to find significant causal connections.This approach is usually called a black box methodology.

The black box methodology approach does not allow the finding and analysis of deeper causal connections that are the proper cause of calculated changes of projectile trajectory.In the case when a deeper analysis of the effect of non-standard conditions on projectile trajectory is required it is necessary to return to the “old”perturbation theory.This perturbation theory is the basis for the creation of perturbation projectile trajectory models.

The above mentioned findings can be documented e.g.on the content of the research report[17].The authors of the report used the black box projectile trajectory model and consequently they were not able to clarify a number of observed phenomena.

The perturbation projectile trajectory models come from the general perturbation theory that was introduced by H.Poincar′e(The problem of three bodies)in the mid-1890s.The first perturbation projectile trajectory models were built during WW1 especially in France,Germany,and the USA[18-20]but achieved results were published in most cases after WW1 between 1919 and 1922,e.g.Ref.[20]and data[10,11].Among the authors of these models are mentioned the′French M.Garnier,M.Haag,K.de F′eriet,H.L.Lebesgue,E.Borel and G.Darrieus[10,11,18-20];German K.Schwarzschield[11,19];American G.A.Bliss[11,21,22]and Bulgarian K.Popoff[11].

The perturbation theory had been developing and widely used at least up to the early 1960s,e.g.Refs.[10,11,22,23].Works published in the following years usually contain only brief notices on this theory and its use in exterior ballistics but the perturbation theory is still in use e.g.for analyses of satellite and cosmic vessels interplanetary trajectories.

There has been an increase in interest focused on the use of perturbation theory during recent years and not only in the connection with compilation of new firing tables or revisions of existing ones[24,25].The authors of Ref.[25]attempted to use a perturbation model but appear to have encountered problems applying it.

Reasons that returned the authors of this article to perturbation theory and models are summarized in chapter 1.Even nowadays,when the use of tabular firing tables is treated as an emergency method for preparation of aiming angles in case of ballistic computer failure,the knowledge of perturbation theory and its utilization in ballistic domain has its importance and meaning.It should be also noted that a majority of developing countries usually do not use the ballistic computers due to financial and other reasons and the use of firing tables is the essential way of preparation of the aiming angles.

The main output from the perturbation models are the WFFs.Their shape depends also on the ballistic coefficient c,muzzle velocity v0,and departure angle θ0,or height of trajectory vertex YS=f(c,v0,θ0).Considering the combinations of the types of projectiles(c),charges(v0),and height of trajectory vertices YSyields a large number of WFFs for MET conditions-wind(range wind wxand cross wind wz),air density and Mach number(“air elasticity”or virtual temperature).The main problem is the reduction of number of WFFs to an acceptable level.This reduction is based on the weighted averaging of selected group of WFFs.A WFF created by averaging is considered to be a representative of a corresponding group of WFFs.Use of the reduction always leads to a decrease in the accuracy of ballistic corrections.

Already during WW1 the number of WFFs was significantly reduced.The reduction was caused by limited abilities to measure the required MET data.At the end[26,27]only two groups of WFFs or Weighting Factors(WFs)were used.One group was used for surface-to-surface fire,the other for anti-aircraft fire.Each group contained subgroups WFs/WFFs for wind w,air density and virtual temperature.Each subgroup was further divided for different trajectory vertex heights YSi,i=1,2,… -see Section 3.2.This system was called “onemessage”system[27].

At the beginning of 1920s this system was criticized due to its inaccuracy in the USA.From 1919 the “three-message”system was developed;firstly WFF for wind and consequently for density[27].It means that for the same height of trajectory vertex three different systems of WFs were used.This system was gradually introduced from 1927.Three MET messages labelled A,B,C were compiled although message C was used also for anti-aircraft fire.It was determined in a table[27]for each gun/mortar,type of projectile and charge which of messages A,B,C should be used for calculations for a given angle of departure θ0.From Ref.[22]it can be deduced that the “three-message”system was still in use in the early 1950s in the USA.

Ratification of STANAG 4061[12]in 1957 meant a return to the less accurate “one-message”system-Fig.7;the literature available does not contain any substantiation of this step.The Eastern block(USSR and its satellites)opted for a different approach,as mentioned in chapter 1.The system of traditional WFs was completely abandoned in these countries and replaced with the system based on the reference height of trajectory(RHT)YR(c,v0,YS).Nowadays western countries still use WFs whereas the ex-Eastern block countries use RHTs.Because of this fact it is not possible to carry out any comparison easily.

This article should be treated as an introduction,summarizing basic findings from the domain.Detailed analyses of partial problems will be published afterwards.Therefore the main aim of this article is to create the prerequisites for a comparison of both methods,especially with respect to the accuracy of predicted results.Another aim of this article is to point out selected shortcomings of both methods.Pros and cons of the Eastern block methodology based on the RHT are discussed across the whole article.

The main contribution of the article is a detailed derivation of relations for the calculation of the reference height of trajectory RHT.A detailed approach was chosen because the traditional approach is very unclear[2,9,15,16]and contains gross errors-there is no explanation why the causality principle is violated,see Section 4.4.The presented examples show how to calculate the RHT for data-WFs published in Ref.[12]-Fig.7 and it allows comparison of results from both methods.

In the case of the “one-message”system according to Ref.[12]there exist two problems,greatly simplified WFF for virtual temperature(“air elasticity”)and wind.Calculation of WFF for virtual temperature[11,22,23]was described in Ref.[28].The authors followed up this article in Ref.[29]and this article briefly deals only with the issues of WFF for wind.The WFF for range wind wxfundamentally differs from the corresponding WFF for cross-wind wz[10,11,21-23].The “one-message”system incorporates both WFFs into a single one for a wind w that blows in an arbitrary direction with respect to the direction of fire.The utilized procedure for combining WFFs has not been found in available literature.Therefore it was estimated as a weighted average.The issue is illustrated by numerical examples-Figs.5 and 7.

Fig.1.Weighting factor function for wind(example of the convex shape)rA,w,n(sy)for n=9,y(9)=6000 m,S=0.356,syR1=0.288,yR1=1730 m,YR=7700 m.

Fig.2..Weighting factor function for air density(example for the concave shape)rR,ρ,n(sy)for n=15,y(15)=18 000 m,S=0.640,syR2=0.720,YR=yR2=13 000 m.

3.Weighting factor functions

3.1.General information

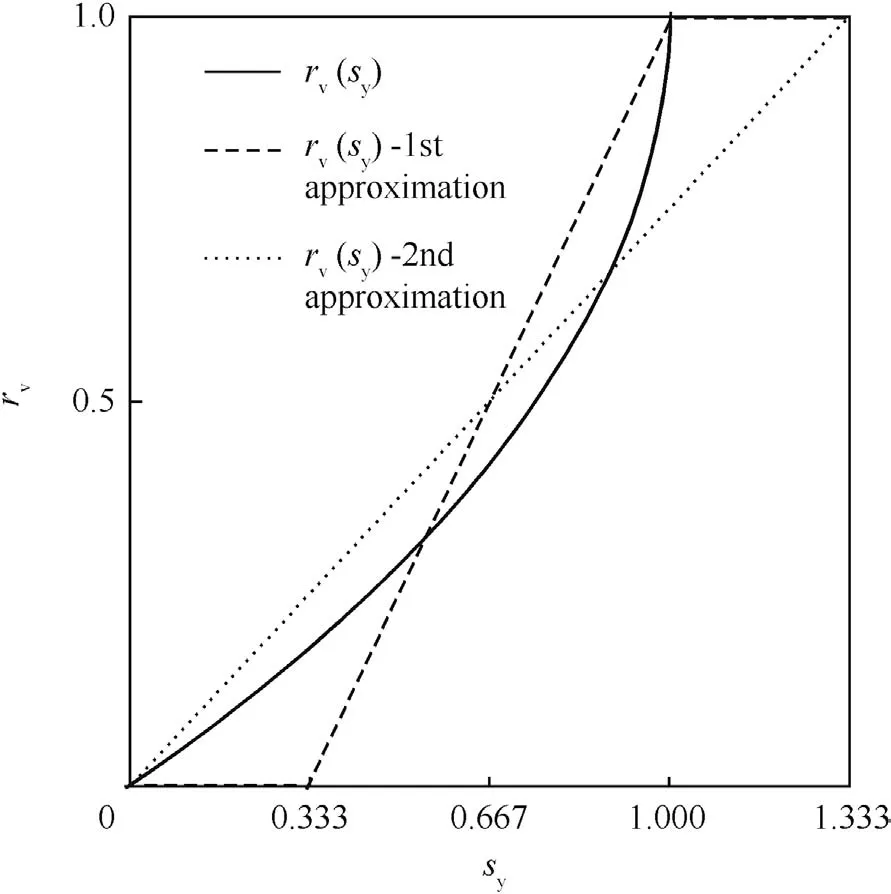
Fig.3.Weighting factor function-vacuum(example of the convex shape)rV(sy),formula(4),S=0.333,syR1=0.333,sYR1=1.333.

Fig.4.Reference height of the trajectory(RHT,YR),nomogram for 122 mm H D-30(2A18),HE projectile OF-462 and charges full,reduced,2nd and 4th.

WFFs r(μ)are usually calculated only for standard conditions(weather,position,material),see Refs.[9,30].WFFs are functions of ballistic coefficient c,muzzle velocity v0,angle of departure θ0.The ballistic coefficient c is defined in accordance with F.Siacci and drag law M1943(c43(m2/kg))in this article.In practice and in accordance with the tabular firing tables the type of projectile and its standard surface finish type instead of c,charge number instead of v0,trajectory vertex height YSinstead of θ0are presented,i.e.r(μ,(projectile,charge,YS)).WFF is calculated for perturbation(δx,δy,δz,δt)in an arbitrary projectile trajectory point and time(x,y,z,t),i.e.r(μ,(projectile,charge,YS),(x,y,z,t)).In the case of indirect fire,the perturbations are most important at the point of impact(y=0),especially perturbations of range of fire δX,time of flight δt(X)and azimuth corrections δZ.This article deals only with perturbations of range of fire δX,i.e.r(μ,(projectile,charge,YS),X)and azimuth correction for the cross wind δZ(wZ).Because the ambiguities are excluded the shortened notation r(μ)instead of r(μ,(projectile,charge,YS),X)will be used hereafter.

Two forms of notation for range correction are used in the tabular firing tables,see Refs.[9,30].

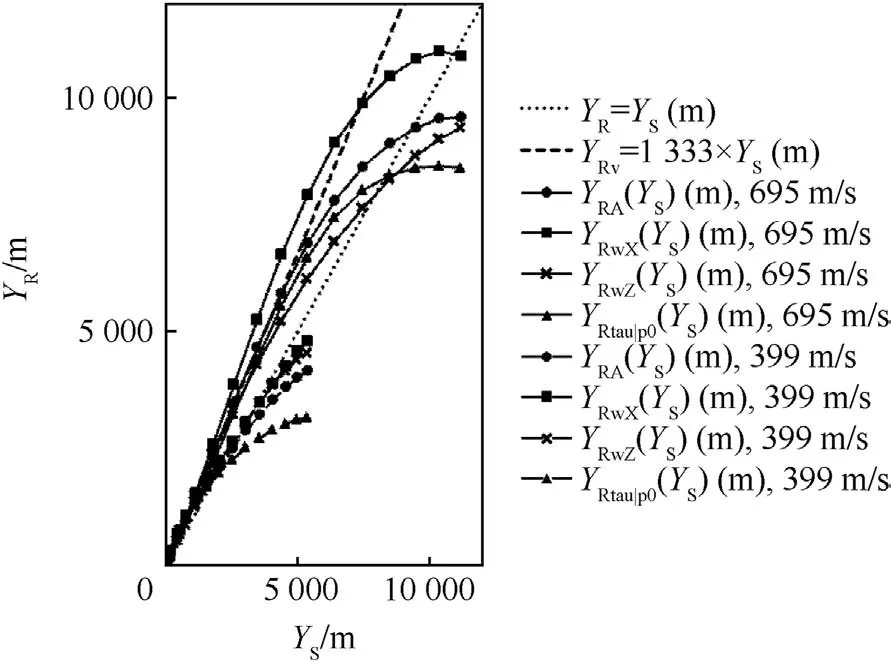
Fig.5.Reference heights of the trajectory for 152 mm SPH,HE projectile OFd,Charge Full(695 m/s)and 4(399 m/s)and θ0=5,10,15,…,70?and YRv(YS)for vacuum is presented for the comparison.

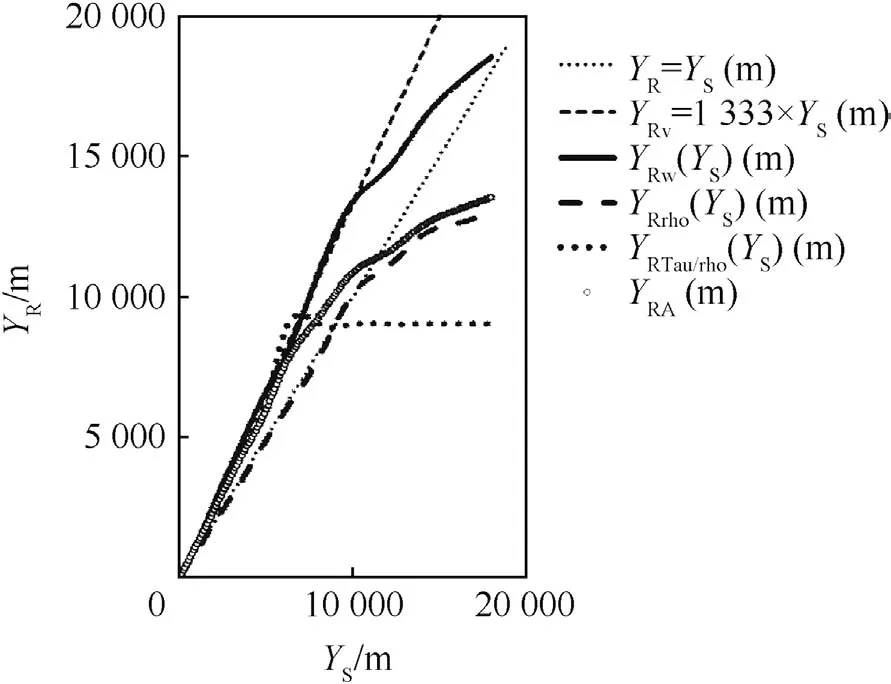
Fig.6.Reference height of the trajectory(RHT):YR,w(YS),YR,ρ(YS),YR,τ|ρ(YS)and YRA(YS)determined for WFFs calculated from WFs presented in Ref.[12]for K=3,and YRv(YS)for vacuum is presented for the comparison.

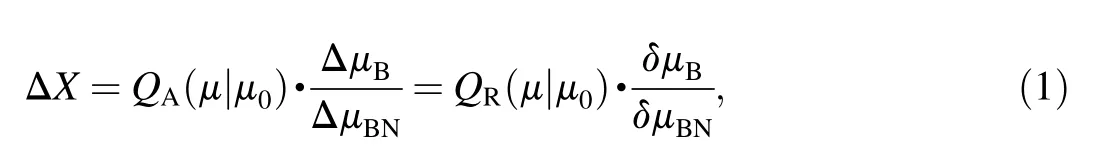
where

ΔμB= μBμSTD-absolute ballistic deviation of ballistic element μB,

δμB= ΔμB/μSTD-relative ballistic deviation of ballistic element μB,

ΔμBN,δμBN-constant norm values of the absolute and relative ballistic deviation that are presented in tabular firing tables,QA,QR-corresponding correction factors for range that are presented in tabular firing tables.

The notation Q(μ|μ0)means that the correction factor Q(μ)is calculated under the assumptions that as a second correction factor is used Q(μ0)and their common range correction ΔXcom= ΔXμ+ ΔXμ0.

Fig.7.Comparison of RHT YRw(YS)determined for WFF calculated from WFs published in Ref.[12]for K=3 with RHTs YR,wx(YS),YR,wZ(YS)and YRA,w(YS)=0.75·YR,wx(YS)+0.25·YR,wZ(YS)calculated for c43=0.43 m2/kg.YRv(YS)for vacuum is presented for the comparison.

Special attention is paid to combinations(τ|ρ)and(τ|p0),where p0is the atmospheric pressure at the gun muzzle level.Reasons for the use of various combinations(μ|μ0)are explained in Ref.[11].

Relations analogous to(1)can be derived for the azimuth corrections δZ.

In case of the wind(w,wx,wZ)the absolute ballistic deviation ΔμB=wB,wxB,wZBis always used because the standard magnitude of the wind speed is equal to zero.The subscript B is not usually used so it is necessary to emphasize that the ballistic wind and its components are meant.In the case of the air density the relative ballistic deviation δμB= δρBis always used.This relative ballistic deviation is used only for the calculation of the trajectories of anti-aircraft projectiles according to Soviet methodology.

For the virtual temperature either relative ballistic deviation δμB(τ|ρ)= δτBin accordance with[8,30]or absolute ballistic deviation ΔμB(τ|p0)= ΔτBin accordance with the Soviet methodology[9,13]are used.

It follows from the above that it is possible to compare directly,without recalculations,only the absolute ballistic deviations ΔμBfor the wind or wind vector.Further in the article only the relations valid for the wind will be compared.

The following definitions hold true[2,11,15,16,22,23]

where

sy=y/YS-relative magnitude of y coordinate,

Δμ(y)= μ(y) μSTD(y)-absolute deviation of met element μ in height y,

δμ(y)=Δμ(y)/μSTD(y)- relative deviation of met element μ in height y,

μ(y)-real or measured magnitude of met parameter μ in height y,

It is obvious that ballistic elements ΔμBand δμBare calculated as a weighted average of measured magnitudes μ(y).

The conversion relation between the WFF rAμ(y)and rRμ(y)is not shown here.The diagrams of WFF rAμ(sy)and rRμ(sy)are usually utilized.Further in the article only the relations following from(2)will be presented because of formal similarity between(2)and(3);this is in agreement with the preference of analysis focused on the wind vector.The subscript A will not be further used unless it leads to any ambiguities.

The WFF derived for the projectile trajectory in vacuum is often utilized[10,11].

This WFF will be further referred as “WFF-vacuum”,see Fig.3.

3.2.Discretization of weighting factor functions

The met messages works with the height zones i,i=1,2,…,nmax.For the height of zone it holds true

where

yZi-upper limit of ith zone,

yZi1-lower limit of ith zone,that is identical with upper limit(i 1)zone,

yZ0=0 m-corresponds to the level surface of the Meteorological Datum Plane(MDP).

Following conversion formula holds true

where hZGis the gun elevation above MDP.

It is valid for the upper limit of the nth zone

and consequently with the use of(6)the corresponding magnitude of y(n)is determined and also sy(n).Magnitudes of y(n)correspond to discrete magnitudes YS=YS(n).In the case when the YSare given and YS(n 1)＜YS＜YS(n)applies it is necessary to find the corresponding magnitudes,that are further shown,by means of interpolation between YS(n 1)and YS(n).

Magnitudes of weighting factors WF are presented always for i=1,2,…,n?nmax

where r0(n)=0,and thus for discrete magnitudes of WFF the equation below applies

because it always applies r(YS)=r(sy)=1 for sy=1,it also applies rn(n)=1.

The literature [2] assumes that nmax= 21,yZ(nmax)=30 000 m.Magnitudes of WF qi(n),i=1,2,…,n are shown only for n?15,yZ(15)=18 000 m.From presented magnitudes(K=2,3)WF the discrete courses of WFF rj,μ,n(sy)for sy=syj,j=1,2,…,n,μ =w,ρ,τwere recreated.It was assumed for simplicity that hZG=0 m.Discrete magnitudes were approximated by suitable continuous functions rA,μ,n(sy)and rR,μ,n(sy).Illustrative examples are presented in Figs.1 and 2.

Discrete magnitudes of partial derivatives are defined by

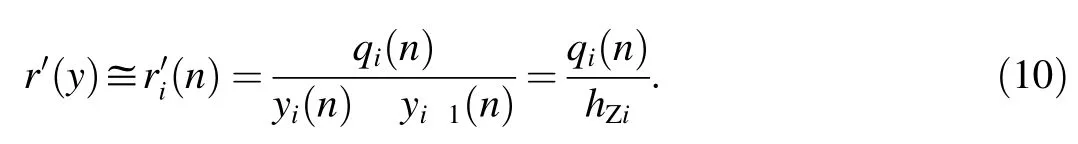
After substitution into(2)and rearrangement it will approximately apply[2,11,12,14-16]

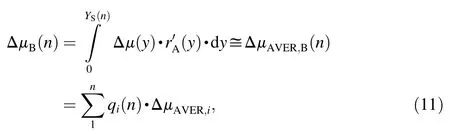
where

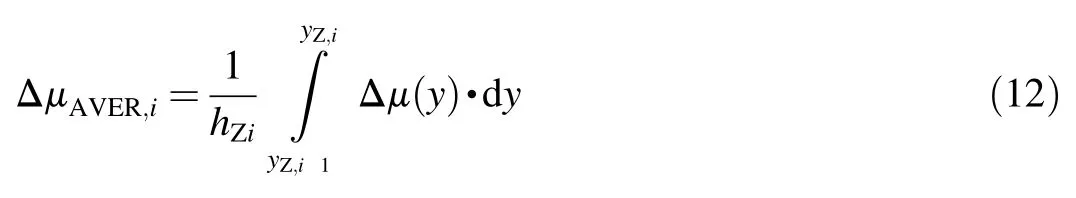
is the average magnitude of Δμ in ith zone.Ways of measurement of Δμ(y)are described in Refs.[2,31],ways of approximate calculation of ΔμAVER,ican be found in Refs.[2,14,24].

4.Reference height of the trajectory

4.1.General information

As it was stated in Section 3.1,the WFF depends,not only on the trajectory vertex height YS,but also on the type of projectile(c)and charge(v0).It means that the WFs presented in Ref.[12]are correct only for a particular calibre,type of projectile and charge.From these facts follow the essential source of errors in the determination of ballistic elements μBor ΔμBand δμB.

Magnitudes of the WFs shown in the Standard Ballistic Meteorological Message[12]are practically used for all calibres,types of projectiles,and charges.

Based on the simulations carried out,it is probable that the WFs are sufficiently accurate for standard projectiles of calibre of 175 and 203 mm and high charges(v0=900-950 m/s).The differences between the WFs mentioned in Ref.[12]and real ones increase with a decrease in the calibre of the projectile(bigger difference in ballistic coefficients)and also with change of charge(lower muzzle velocity v0).The differences also increase for angles of departures above 50?.

The other hypothesis is such that the WFs in Ref.[12]were created by weighting of WFs determined from different WFFs calculated for selected combinations of c,v0,θ0.Also in this case the limitations mentioned in the previous paragraph are true.

The standard[12]comes from the 1950s(ratified 1957)and so it would be very difficult to get the original source materials.

A similar methodology to that described in Ref.[12]was also used in the former USSR.But in the 1950s(probably before 1956)a new methodology was proposed probably with the aim to overcome the deficiencies mentioned.This new methodology was gradually introduced into practice within following 10 years not only in the USSR but also in its satellites.In general,it was widely used since 1970s.This new methodology eliminates the deficiencies mentioned but introduces new ones as explained later in the article.

The important fact is that METEO-11 or-44 provides the following average values,i.e.not weighted values

and its discrete estimation

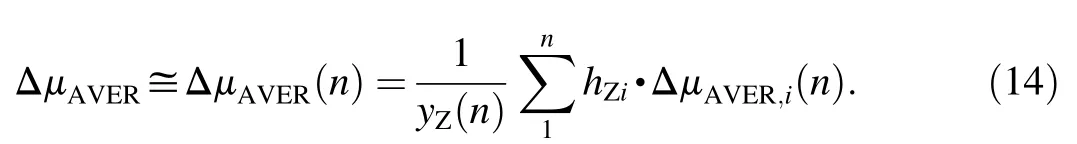
Similar relations hold also true for δμAVERand δμAVER(n).It follows from the above paragraphs that data contained in the met message METEO-11 and-44 have a general validity similar to data in the met messages METGM[4]and METCMQ[5],i.e.data independent on the type of projectile,charge,and angle of departure.

The essential simplification is based on a simplification of the WFF only by two WFs q12,q22for intervals 〈0,yR〉and〈yR,YS〉.Two values ΔμAVER(yR)and ΔμAVER(YS)follow from the relation(13).Simultaneously only two possibilities(q12=0 and q22=1)or(q12=1 and q22=0)are valid and the aim is to find suitable approximation relations for the RHT yR.

Introducing estimates of partial derivatives

and their substitution into(2)

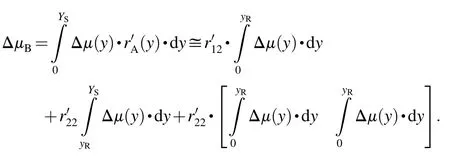
After the rearrangement the essential calculation relation is obtained

where

is the average ΔμAVER(y)on the interval〈yR,YS〉.

If it holds true that YS(nR1)＜yR＜YS(nR)or also YS(n 1)＜YS＜YS(n),it is necessary to carry out one or two interpolations in the data from METEO-11 or-44.

Finally the area below the WFF is determined

The WWFs are consequently divided into two groups:WFFs of a convex shape(S＜0.5;yR=yR1),see the example in Fig.1 and WFFs of a concave shape(S?0.5;yR=yR2),see the example in Fig.2.It is necessary to carry out the analysis for the determination of RHT yRseparately for each group of WFFs.Whether the WFF is of convex or concave shape depends on weapon and ammunition characteristics,atmospheric conditions,and angle of departure θ0(height of trajectory vertex).

4.2.Concave shape of the weighting factor function

The magnitude of syR=syR2is determined from the equality of the complementary area(1 S),see Fig.2 and the corresponding area of triangle 0.5·syR2,and subsequently

Usually syR2=from(0.5-0.7)up to 1.0.Height yR2is approximately equal to the RHT.Essential relation(17)is reduced into(q12=1 and q22=0)

The ballistic element ΔμB(YS)is determined very simply because it is equal to ΔμAVER(yR),yR=yR2is obtained by interpolation between data from METEO-11 or-44.

4.3.Convex shape of the weighting factor function

The magnitude of syR=syR1is determined from the equality of the area S,see Fig.1 and the corresponding area of triangle 0.5·(1 syR1),and subsequently

Usually syR1=from 0.0 up to 0.4.Height yR1is an estimate of the RHT.Essential relation(16)is rearranged into(q12=0 and q22=1)

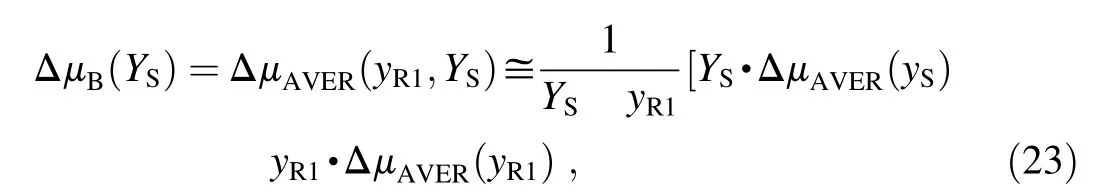
The ballistic element ΔμB(YS)is determined in a more complicated way than in the previous case because it is equal to ΔμAVER(yR,YS),yR=yR1is obtained by calculation(utilizing(18)or(23))from values ΔμAVER(yR1),ΔμAVER(YS)is obtained by interpolation between data from METEO-11 or-44.

4.4.Violation of the causality principle

The authors of the original methodology probably regarded the relation(23)and activities connected with it as complicated and as a possible source of errors during manual calculations.Due to these reasons they decided to simplify the procedure but at the expense of violation of the causality principle.

The authors proceed from an empirical finding that the behaviour of ΔμAVER(y)under usual meteorological conditions is nearly linear

Under this assumption the relation(23)will have a form

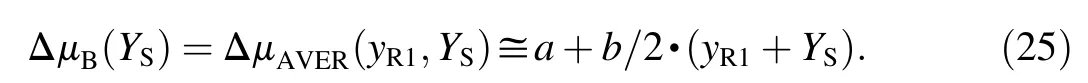
Now the new RHT YR1is searched for which is

After that for the new RHT the following equation applies

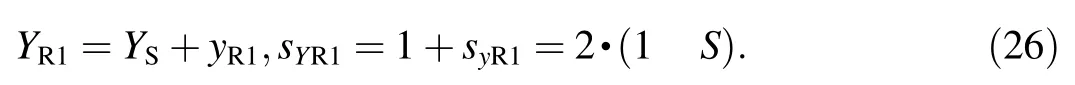
On the basis of this the following simple relation holds true

For example for the WFF-vacuum,S=1/3,syR1=0.3333 and sYR1=1.3333,see Fig.3.

The ballistic element ΔμB(YS)is determined in a very simple way,because it is always equal to ΔμAVER(YR1)corresponding to RHT YR1.The magnitude of ΔμAVER(YR1)is obtained by interpolation in METEO-11 or-44.

The original methodology[2]shows only a unified relation(compare relations(20)and(26),YR2=yR2)for calculation of the RHT

although the derivation of this relation is not correct but another relation is not published in the available literature.

The ballistic element ΔμB(YS)is determined in a very simple way,because it is always equal to ΔμAVER(YR)corresponding to RHT YR.The magnitude of ΔμAVER(YR)is obtained by interpolation in METEO-11 or-44.

4.5.Average reference height of trajectory

As was shown at the end of Section 2,the WFF for the wind rw(y)is a weighted average of two WFFs rwx(y)and rwZ(y).Also the original Soviet methodology assumes calculation of a weighted average of three WFFs rAwx(y)and rAwZ(y),and rA,τ|p0(y).But only their arithmetic mean is calculated in practice and it is equivalent to calculation of the arithmetic mean of the corresponding areas Swx,SwZ,and Sτ|p0determined by(19),or corresponding RHT determined by(28).

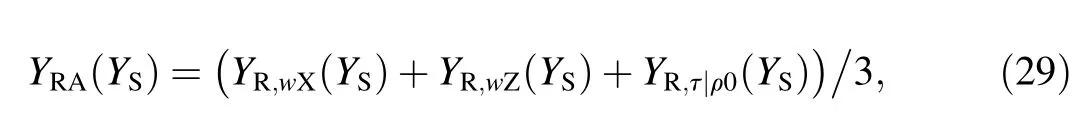
The tabular firing table contains average RHT YRA(YS)rounded to hundreds of meters.During the introduction of the METEO-11 and-44 into practice the nomograms were used,see Fig.4.

It can be assumed that the author of the Soviet methodology used a single average RHT YRA(YS)instead of three RHTs YR,wx(YS),YR,wZ(YS)and YR,τ|p0(YS)either due to reduction of probability of mistaking of individual nomograms or due to reduction of amount of data published in the tabular firing tables.

Generally it is possible to use three independent RHTs and thus lowers the error in determination of the ballistic elements(wx,wZ,Δτ)B,as is obvious from Fig.5.In such a case the errors of their determination are given only by the linearization of the WFFs and by the violation of the causality principle,for situations when YR＞YS.It is not necessary to use the causality violation principle but it is possible to utilize the more accurate relation(23).

Application of the described process on the methodology considered that is derived from WFs published in Ref.[12],requires the weighting of WFF rA,w(y),rR,ρ(y)and rR,τ|ρ(y).It holds true for average RHT

Corresponding dependencies are shown in Fig.6.

5.Conclusion

Simplifications for the weighted average YR,wx(YS),YR,w-Z(YS)with the aim to obtain YR,w(YS)and also based on weighting average across various combinations of(c,v0,θ0)were discussed on the example of the ballistic wind and use of Fig.7.

Fig.7 shows dependencies of RHTs YR,wx(YS),YR,wZ(YS)and YRA,w(YS)=0.75·YR,wx(YS)+0.25·YR,wZ(YS)calculated for c43=0.43 m2/kg,v0=600,900 m/s and θ0=5,10,15,…,70?.The magnitude of the ballistic coefficient c43=0.43 m2/kg is close to that of projectiles of calibre of 175 and 203 mm.It is obvious from the behaviour of YR,wx(YS),YR,wZ(YS)that their effect on the projectile trajectory is very different.It is questionable whether their dependencies should be replaced with their weighted average YRA,w(YS).

From the comparison of RHT YRw(YS)determined for WFFs calculated from WFs presented in Ref.[12]for K=3 with average RHT YRA,w(YS),it is obvious that large errors result from neglecting the effects of muzzle velocity v0and angle of departure θ0.Analogously the effect of change of ballistic coefficient c,e.g.due to change of calibre,can be proved.

On the basis of the research carried out the authors are inclined to think that the Soviet methodology offers a higher potential for the reduction of errors arising from its use than the methodology utilizing[12].

Further work will be focused on the analysis of errors arising from the use of both methods.For this purpose a large database of meteorological measurements carried out during a whole year in different places of the Earth will be utilized.

Acknowledgements

This work originated under the support of financial means from the industrial research project of the Ministry of the Interior of the Czech Republic - project code VG20122015076:“Two survey points range-finding system utilization for perimeter security(screen)”and from the Research project for the development of the Department of Weapons and Ammunition,Faculty of Military Technology,University of Defence,Brno,PRO K-201.

We would like to express our sincere thanks to Dr.Clive R.Woodley,Qinetiq,UK,for his valuable remarks during preparation of English version of this paper.

[1]STANAG 4635.The NATO error budget model.

[2]Kovalenko VV,Shevkunov VI.Meteorological preparation of artillery if re(in Russian).Leningrad:Military Artillery Academy of M.I.Kalinin;1975.p.84.

[3]STANAG 4044.MET adoption of a standard atmosphere.

[4]STANAG 6022.METadoption of a standard gridded data meteorological message(METGM).

[5]STANAG 4082.MET adoption of a standard artillery computer meteorological message(METCMQ).

[6]STANAG 4355 JAIS.The modified point mass and five degrees of freedom trajectory models.

[7]Longdon LW,et al.Textbook of ballistics and gunnery,vols.1 and 2.London:Her Majesty's Stationery Office;1984 and 1987.p.806,521.

[8]STANAG 4119.Adoption of a standard cannon artillery firing table format.

[9]Logvin AM,Aleksandrov VI.Gunnery and exterior ballistics(in Russian).Penza:Military Artillery Academy of N.N.Voronov;1977.p.255.

[10]Curti P.Introduction into exterior ballistics(in German).Frauenfeld:Verlag Huber and Co.;1945.p.408.

[11]Molitz H,Strobel R.Exterior ballistics(in German).Berlin:Springer-Verlag;1963.p.610.

[12]STANAG 4061.MET adoption of a standard ballistic meteorological message(METBKQ).

[13]Composite Authors.Del-55-26 fire and fire control of the field artillery(in Czech).[Textbook].Prague:Ministry of Defence of the Czechoslovak Socialistic Republic;1981.p.856.

[14]Composite Authors.Meteorological preparation of artillery-temporary edition(in Czech).Prague:Ministry of Defence of the Czech Republic;1998.p.115.

[15]Petrovic DR.Mechanized procedure for the calculation of altitude coefficients.Sci Tech Rev 2005;LV(3-4):9-14.

[16]Petrovic DR.New procedure for calculating altitude coefficients.Sci Tech Rev 2006;LVI(3-4):47-51.

[17]Composite Authors.Enhanced MET accuracy test trial.KerMET fire report 2008.Test firing in Turkey;November 2006.NATO/PfP Unclassified,PfP(NAAG-LCG/3-SG/2)and MCMG/WG-BMWG.p.337.

[18]Aubin D. “I'm just a mathematician”:why and how mathematicians collaborated with Military Ballisticians at G^avre.Paris:HAL-UPMC,Pierre and Marie Curie University;2010.pp.801-42.

[19]Aubin D,Goldstein C.Placing world war I in the history of mathematics.Paris:HAL-UPMC,Pierre and Marie Curie University;2013.pp.1-54.

[20]D'Adh′emar R.La Balistique ext′erieure.Paris:Gauthier-Villars;1934.p.55.

[21]Bliss GA.Functions of lines in ballistics.Trans Am Math Soc Apr.1920;21(2):93-106.

[22]McShane EJ,Kelley JL,Reno FV.Exterior ballistics.University of Denver Press;1953.p.834.

[23]Bliss GA.Mathematics for exterior ballistics.London,Printed in USA:John Wiley and Sons,Inc.;1944.p.128.

[24]Zhaosheng W,Xifu G.Firing errors caused by using ballistic mean of meteorological element to calculating firing data.In:Proceedings of 20th International Symposium on ballistics,Orlando,FL;2002.pp.131-8.

[25]Essoloh M,Huguet P,Collin G.Artillery meteorology.MET coefficients.(Presentation),DGA France,MILMET 6-November 20-22,2013,Brusselles.p.11.

[26]Composite Authors.A course in exterior ballistics.Ordnance textbook.Ordnance Department,December 1920.Washington Government Printing Office;1921.p.127.

[27]Edgecomb FE.Meteorology for artillery.Coast Artill J September 1928;69(3):203-11.

[28]Roth E,Sägner R.On effect of temperature on projectile trajectory(in German)Z für angew Math Phys 1962;13(2):175-81.

[29]Cech V,Jedlicka L,Jevicky J.Some problems with the estimation of projectile trajectory perturbations.In:Book of full texts of the 20th International Conference Engineering Mechanics 2014,Svratka,Czech Republic,May 12-15,2014.116-9.

[30]Composite Authors.Tactics,techniques and procedures for field artillery.Manual Cannon Gunnery,Department of the Army;1996.FM 6-40,p.757.

[31]Composite Authors.Federal meteorological handbook No.3,Rawinsonde and Pibal observations.U.S.Department of Commerce;1997.FMC-H3-1997,p.191.