Experimental investigation of a cook-off temperature in a hot barrel

Amer HAMEED*,Mathew AZAVEDO,Philip PITCHER

aCentre for Defence Engineering,Cranfield University,Defence Academy of the United Kingdom,Shrivenham SN6 8LA,United Kingdom

bCranfield University,Defence Academy of the United Kingdom,Shrivenham SN6 8LA,United Kingdom

1.Introduction

As the gun fires,the chamber surface temperature increases due to propellant burning.If it continues to fire at a high rate,the chamber surface temperature will continue to increase with every firing.During this event,if the propellant cartridge is loaded in the hot chamber,the heat transfer from chamber to propellant will take place.As the propellant heats up,the thermal decomposition reaction initiates,and in the limit it could lead to thermal explosion or ‘cook off’.The rate at which the chamber heats up defines the operational limit of the weapon and its ammunition propellant.Therefore it is important for both the weapon designer and the safety inspector to understand and appreciate this thermal limitation while designing the weapon and defining the appropriate rate of fire and storage procedure.Currently operational and training limits for hot gun weapons are typically defined in terms of a set number of rounds in a specified time period.A further understanding of the cook-off mechanism will allow development of systems,particularly in platform mounted weapons,where the hot gun limits can be based on weapon temperature readings.

In the event of a chambered round in a hot gun,the standard means of dealing with the situation is to leave the weapon on target,or in a known safe direction,for the duration of the safe cook-off wait-time.This necessitates remaining in contact with,and being exposed to,the target for the duration of the period.In the case of man-portable small arms,this is likely to mean an increase in exposure while weapon arcs significantly constrain manoeuvr ability in a larger platform.

By further understanding of cook-off mechanisms,and therefore of the time and temperature limits of the reaction mechanism,such operational constraints can potentially be reduced.An increase in the temperature at which the weapon is considered to be in a too hot will allow greater flexibility in firing rate before overheating.An accurate understanding of the cook-off reaction times for the weapon at a specific temperature can reduce the safe wait-time and allow manoeuvring sooner.In addition,understanding the minimum time before a reaction occurs may allow action to be taken,such as ejecting the round to prevent the reaction from occurring.

Fig.1.Heat generated in(G)and loss(L).

2.Propellant cook-off in hot gun

In a system where there is a cook-off event,cook-off arises due to an acceleration of the heat released by the internal decomposition reaction that is greater than the degree of cooling.This may be due to the weapon being hot,which causes a high temperature difference and induces a rapid heat gain within the round,or alternatively low levels of heat loss preventing the reaction from taking place.

In a gun system,heat is lost from the system at a rate which is dependent on the conditions at the boundary of the system.Each system can be considered to be made up of two curves representing heat generation(G)and heat loss(L)which are independent but interact to form the system heat balance.The thermal behaviour of the system can be described by Eq.(1)[3]below.

where m is propellant mass and cvis specific heat.While the rate of heat being generated by the system is an exponential function,governed by the Arrhenius equation,the heat loss from the system is a linear function based on the boundary conditions.When heat loss is subtracted from heat generated as shown in Fig.1,the change in thermal energy is obtained.

The gradient of L is set by the heat transfer properties of the boundary while the x-intercept(T0)is the ambient temperature at the boundary of the system.From this if the system temperature is higher than T0,there is a net heat loss from the system,however if the system temperature is lower than T0,L will be negative and there will be a net heat flow into the system.

From Fig.1,it can be seen that,for heat curves G3and L2,a stable region exists below TBin which temperatures will tend to TA.For a small temperature increase above TA,heat loss L is greater than heat generated G,and therefore the temperature will decrease to TA.Similarly,the temperatures below TAwill increase as heat gain G is greater than heat loss L.At temperatures above TB,there exists an unstable state where heat gain G always exceeds heat loss L and thermal runaway commences.

For the systems where L is minimal when compared to G,such as with G1and L2,there is no capacity for a stable condition to exist and the system always undergoes thermal runaway.As L decreases further as compared to G,there exists a situation where the system is thermally stable at only one temperature,as can be seen from G2and L2,and is unable to withstand any temperature increase without undergoing thermal runaway.

3.Cook-off situation

In a weapon cook-off situation,Tcis the barrel temperature and therefore L is a significant portion of the temperature profile.This has the effect of reducing the stable region between TAand TBto the point where there is no overlap between G and L.Under these conditions,the system is always in a state of thermal runaway and the system temperature is accelerated by the external conditions,as given in Eq.(2).

Fig.2.Test apparatus:(a)unloaded,(b)loaded and(c)activated.

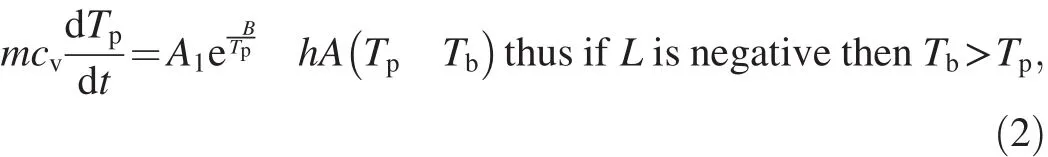
where A1is propellant pre-exponential,B is propellant activation energy,h is heat coefficient and A is propellant surface area.

Cook-off reaction occurs due to a temperature increase causing an acceleration of the internal decomposition reaction that exceeds the rate of heat loss.This may be due to the hot weapon causing a high temperature difference between barrel and powder so that heat gain within the round exceeds heat loss.

4.Hot chamber testing apparatus

For the experiments,a unique test apparatus was designed to simulate a gun barrel and cartridge in a cook-off situation.In order to achieve this,the test apparatus is designed to heat a chamber with 175 W heater elements,insert a cartridge remotely filled with propellant and manage the cook-off reaction without localised damage.The apparatus,shown in Figs.2 and 3,is also designed to record the centre thermal profiles of barrel and powder while the reaction takes place.

The stages of the test apparatus used are shown in Fig.2,where(a)shows the test apparatus with the simulation barrel raised,(b)shows a cartridge with a known quantity of propellant inserted,and(c)shows the situation after the release pin was pulled and the barrel was dropped into the cartridge.

A number of methods for driving the movement were considered,including hydraulic rams and electric motor drives.However,a drop under gravity was selected to gain reliability through reduced complexity.This had the added advantage of reducing manufacturing complications,critical tolerances,and the number of parts.The final design has a drop of 70 mm and,assuming g=9.81 m s2,a freefall closing velocity from Eq.(3)is 1.3 m s1

where vfis the final velocity,viis the initial velocity,xfxois the drop distance is the drop height and a is equal to g.The experiments conducted were broadly grouped into temperature ranges of the barrel at commencement to provide the basis for comparison and statistical analysis(Fig.4).A graphical representation of the data obtained provides an indication of the overall trend as well as the consistency of the experimental results over the trial.Basic statistical analysis(mean and standard deviation)was used to assess the consistency of the data and to compare parameter behaviour with variation in temperature.

As a result of the initial ignition test which indicated a temperature of ignition in the vicinity of 160°C,the final temperature ranges for tests were selected as 160°C,170°C,180°C,190°C,200°C,220°C and 240°C.These were the chamber temperatures at which the barrel was dropped into the cartridge and is defined as➀ “chambering”in Fig.4.

Description of events shown in Fig.4 are given below:

Chambering point-The commencement point of the trial and nominally the zero time point.Identified as the onset of the initial barrel temperature change after being dropped onto the cartridge.In a weapon firing scenario this is the point where a fresh round is chambered and heat transfer commences.

Start temperature(Barrel)-This is the initial barrel temperature at the chambering point and provides an indication of the heat available for the follow on reactions.

Start temperature(Powder):This is the initial powder centre temperature at the chambering point.Nominally this will be the magazine or ambient temperature of the weapon system.

Delay-The period of time between chambering and the commencement of powder centre temperature rise;this also indicates the time for heat transfer to reach the centre of the powder.

Slump-After chambering the barrel temperature slumps by a certain amount before increasing again until a steady state condition is reached.The slump is measured as the start temperature(Barrel)minus the first minimum after chambering.

Rise rate-The initial,near linear,powder temperature rise expressed in degrees Celsius per minute.Measured from just after commencement of rise until the temperature change rate begins to slow or a cook-off reaction occurs.

Peak(Barrel)-After increasing to a steady state condition the barrel temperature again begins to decline.The peak reached is measured as the maximum barrel temperature between the slump and the end of the experiment recording.

Peak(Powder)-The maximum temperature the powder centre reaches during the experiment.

Cook-off time-The time from chambering to the commencement of the cook-off reaction,identified by a sharp change in rate of change of temperature(in s).

Cook-off temp(Barrel)-The temperature at the commencement of the cook-off reaction.

Cook-off temp(Propellant)-The temperature at the commencement of the cook-off reaction.

Fig.3.Schematic diagram of test apparatus.

Fig.4.Key features of characteristics curves.

Fig.5.Cook-off temperatures and time(plotted on the same axes).

Table 1Time to cook-off 3.890592σ(99.99%of occurrences).

5.Experimental results

The temperatures of both the barrel and propellant at thermal explosion are plotted in Fig.5 following commencement of the thermal explosion reaction along with the event times.The “green”curve represents mean propellant thermal explosion temperature,while the “brick-red”colour represents the mean barrel temperature.From the graph,it can be seen that as the mean barrel temperature increases,the time to thermal explosion reduces.Similarly,with the increase in barrel temperature,the heat transfer rate between barrel and propellant is such that the thermal decomposition initiates earlier and this is a significant observation.From the graph,it can be seen that,in the temperature range of 180°C and 190°C,the propellant centre temperature decreases with the increase in barrel temperature for thermal explosion to occur.Therefore 180°C can be defined as the safe limit for this propellant.From the “blue”curve,it can be seen that it takes around 150-240 s for thermal explosion in this range.

As a means of establishing the safe times associated with a cook-off situation it was necessary to determine the possible times at which a cook-off reaction occurs.A suitable method was to calculate the upper and lower limits of each temperature range where cook-off was observed.For the purposes of this experiment,a range of 3.89σ was used,which equates to 99.99%of possible results,and intervals were determined,as shown in Table 1.

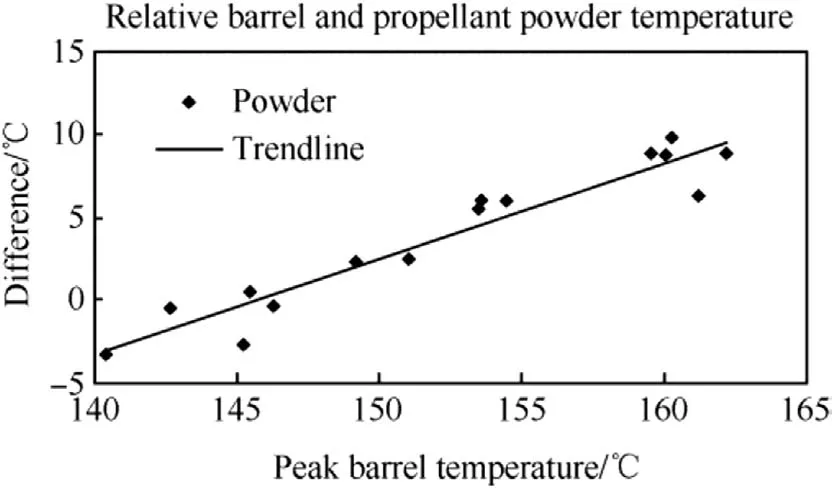
Fig.6.Relative temperature difference between barrel and propellant powder.

Fig.7.Temperature plot of Bulls Eye propellant(160 °C-170 °C).

From the experiments it was observed that the cook-off reaction occurred when initial barrel temperatures were between 169.6°C and 170.1°C.These start temperatures correspond to peak barrel temperatures after activation at the temperatures between 149.2°C and 151.0°C,as well as propellant temperatures between 151.4°C and 153.5°C.It was noted that the propellant temperatures surrounding the onset of cook-off are higher than the barrel temperature.This is expected due to the additional heat generated by the chemical reaction of the propellant decomposing.A plot of the relative powder temperature against the peak barrel temperature over the temperature range from 160°C to 180°C is shown in Fig.6.It can also be seen that,at barrel temperatures above ～146°C,the chemical reaction causes the propellant centre temperature to exceed the peak barrel temperature.At temperatures below ～146°C,the heat generated by the chemical reaction is less than the heat loss through the propellant;whereas the chemically generated heat above this threshold increases the powder temperature above the temperature of the metal,thus transferring heat into the cartridge and driving the reaction.

Fig.8.Time/temperature relationships where cook-off is likely.

Consequently,below this threshold the heat transferred and generated from the internal chemical reactions was not enough to exceed the heat that could be conducted back through the casing and barrel.Although the propellant centre temperature exceeds that of the surrounding barrel,a cook-off reaction does not occur.Fig.7 shows that on heating the powder temperature rises to a plateau where the heat internally generated is being dissipated and equilibrium is established.Any increase in temperature above this level will have a corresponding increase in chemically produced heat and a cookoff reaction will occur.In this series of experiments this was be observed to be between 151.4°C and 153.5°C.

6.Analysis of results

Pitcher[1]previously noted that for the configurations considered here,the critical wall temperature of the cartridge was between 161°C and 162°C.Below the 161°C limit,the propellant was unlikely to cook-off;cook-off was assured above 163°C.However,this did depend on the rate of heat rise;in one experiment using the 200 W heater elements,the propellant core temperature was 156°C at cook-off(compared with the mean average of 162°C-168°C using the 100 W heater elements).Pitcher also stated that cook-off can still occur at a certain heating rate even if the Bulls Eye's core propellant temperature is lower than the wall temperature(recorded as temperature difference between 15°C and 20°C).These cartridges can also be prone to cook-off within 1800 s at a constant cartridge wall temperature of approximately 145°C;the core propellant started thermal runaway at approximately 1600 s until the ignition temperature of 145°C.

For the hot barrel cook-off experiments in Ref.[2],the region where cook-off was likely to occur was bounded by the upper and lower limits and the No-Go region,as shown in Fig.8.There was significant variance in the standard deviations as a percentage of the mean.A likely cause of this was the low population size of 4 or 5 in each temperature range.If the population size was increased through more experiments,it is likely that the lines become more consistent across the temperature ranges.

At start temperatures(barrel)around 185°C,the barrel and powder cook-off temperatures are equal in Fig.5.A pair of equations of straight line for mean cook-off temperatures can be resolved,and an intercept can be simultaneously calculated at a start temperature(barrel)of 186.0°C and cook-off temperature of 163.0°C.At this point,cook-off will theoretically occur and the barrel and propellant will be at the same temperature.Above this point,it can be observed that the propellant temperature at cook-off drops dramatically,while below it exceeds the barrel temperature by a small margin.At higher temperatures,it appears that the propellant closest to the casing reaches the cook-off temperature before the centre significantly heats up[3].In this regime,the heat transfer from the barrel is the dominant heating effect.

7.Conclusions and recommendations

The experiments conducted in this study identified a number of factors to further the understanding of the cook-off reaction dynamics for a chambered round in a hot gun.While the onset of cook-off occurred at a higher barrel temperature than the cook-off temperature of the propellant,it was not significantly higher.The immediate cooling from heat transfer to the cartridge and alignment disk(breech block)was found to briefly reduce the barrel temperature;however it was the rate of cooling of the barrel which dominated the propellant cooling-allowing the cook-off point to be avoided.As higher temperatures were reached,the heat transfer into the cartridge resulted in cook-offoccurring at the outer edge before the central temperature increased sufficiently for cook-off.

It was found that the cook-off temperature of Bulls Eye propellant with the heat transfer profile of the simulation barrel was between 151.4°C and 153.4°C,with the reaction occurring less than 300 s after round chambering.A time vs temperature profile was developed,indicating the conditions in which 99.99%of cook-off reactions are predicted to occur.

A laboratory scale testing apparatus was developed for the experiments,which allows a cartridge to be inserted into a hot simulation barrel with both the barrel and release being remotely operated.The experiment was found to be consistent and repeatable in its operation.

Acknowledgement

The Authors would like to express their thanks to Dr Bryan Lawton for his valuable guidance.

[1]Pitcher P.Assessment of self ignition temperature(cook-off)in gun barrels.MSc Project thesis.Shrivenham,SN6 8LA,UK:Cranfield University;2012.

[2]Azavedo M.Assessment of self ignition temperature(cook-off)in hot gun barrels.MSc Project thesis.Shrivenham,SN6 8LA,UK:Cranfield University;2013.

[3]Markides CN.Advanced autoignition theory:a short(but hopefully sweet)introduction.Available from: www2.eng.cam.ac.uk/～cnm24/images/Autoignition.pdf;2006[accessed 04.06.13].