Distributed Average Consensus in Multi-agent Networks with Limited Bandwidth and Time-delays

Wenhui Liu Feiqi Deng Jiarong Liang Haijun Liu

I.INTRODUCTION

THE distributed consensus problem of multi-agent net

works has attracted great interests in recent years.It has gained wide applications in practice,such as information fusion in sensor networks,load balancing in processor networks,clock synchronization,and multi-agent coordination and flocking.The distributed average consensus usually means to design a network protocol such that the states of all agents asymptotically reach the average value of their initial states as time goes on.In practice,the communication bandwidth and time-delays are important constraint conditions.The conventional consensus protocols are not appropriate for them.Recently,more and more researchers study the distributed consensus problem of multi-agent networks with quantization information and/or time-delays,such as[1-15]and references therein.

There are many distributed algorithms to achieve consensus in literature,for example,classical consensus algorithms,Gossip algorithms[1-3],sequence averaging algorithm[4],etc.Here,we emphasize that the design of efficient quantization ways(namely smart quantization techniques)is very important.In[5-9],they have given some quantization techniques,for example,uniform quantization strategy with finite-level[5,6]or in finite-level[7],the logarithmic quantization strategy[8,9]and the “zoom in-zoom out”uniform quantization strategy[8,9],etc.

In[5,7,9],the distributed average consensus problem of multi-agent systems with quantization information was studied.However,only the real-time communication was considered.In[10],the average consensus problem for multi-agent networks with communication delays and limited data rate was dealt with.Our paper will further consider the distributed average consensus problem of multi-agent systems with limited communication data rate and time-delays.Generally,in order to control and process a complex dynamic network,we do not transform it into a single high-dimensional system by simply increasing dimensions[16].Thus,our paper will not construct a high-dimensional augmented system as in[10].Furthermore,we show that the average consensus protocol((4)in this paper,(5)in[10])is robust to finite symmetric time-delays,but is sensitive to asymmetric time-delays(see Remark 3 in Section III-A).

Another main contribution of our paper is that we study two types of dynamic encoders/decoders.One uses inverse proportion function as scaling function,while the other uses exponential function as scaling function.We prove that all agents can reach average consensus asymptotically with our protocol.We believe that different encoders/decoders have different applications in practice.

The remainder of this paper is organized as follows.In Section II,we present the model of networks,propose a distributed protocol,and formulate the problem to be investigated.Section III presents the main results.We prove that the multi-agent network can reach average consensus asymptotically.The protocol with an inverse proportion function as scaling function is considered in Section III-A,and the protocol with an exponential function as scaling function is considered in Section III-B.Simulation results are given in Section IV.Section V draws the conclusions.

II.PRELIMINARIES AND PROBLEM FORMULATION

In this paper,we consider the average consensus problem for a network of agents with the dynamics of

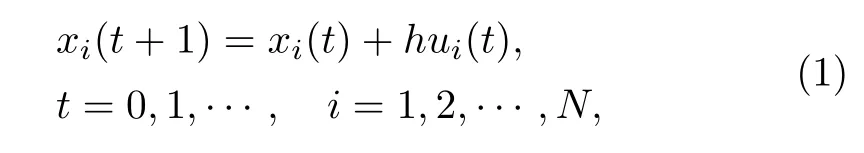
wherexi(t)∈Randui(t)∈Rare,respectively,the state and input of thei-th agent,andhis the control gain.The communications among agents are modeled as a simple undirected weighted graphG=(V,E,A),whereV={1,···,N}is a nonempty set ofNnodes and each node denotes an agent,Edenotes the edge set and each edge denotes a communication channel.

Distributed average consensus control means designing a distributed protocol for the dynamic network,such that the states of all agents converge to the average value of their initial values.

Definition 1.The multi-agent network(1)is said to reach average consensus asymptotically,if for each initial conditionx0:=[x1(0),···,xN(0)]T,

For the multi-agent network(1),a classic distributed average consensus protocol was proposed in[11]as

Thei-th agent needs the exact state information of its neighbours.However,(2)may be too rough when the network links represent actual digital communication channels.For digital networks,only symbolic data can be exchanged among agents[5,9].

Some distributed protocols which use the quantized information were proposed as

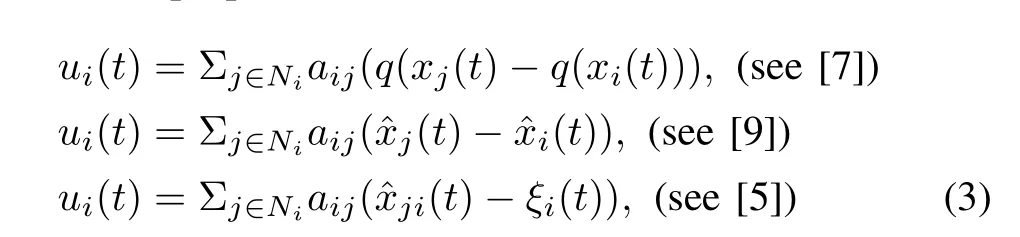
For the practical multi-agent digital network(1),we assume that each agent can only exchange symbolic data with its neighbours and the network has finite time-delays.

We propose a time-delay distributed protocol as

whereξi(t)∈Randˆxji(t)∈Rare,the internal state of Φiand the output of Ψji,respectively(see bellow).

The form of encoder Φi/decoder Ψjiin this paper is similar to the one in[5],but they are not exactly the same.Because we use some different scaling functions for them.

The difference encoder Φiof thei-th agent is given by

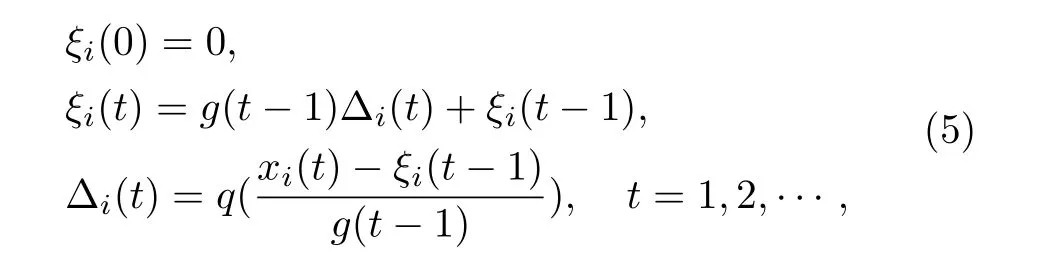
whereξi(t)∈Ris the internal state of Φiand Δi(t)is the output of Φi.Δi(t)will be sent to its neighbours along communication channels.Perhaps these neighbours cannot get data Δi(t)on time.

For each communication channel(j,i)∈E,thei-th agent receives Δj(t),and then uses the following decoder Ψjito recoverξj(t)which is the estimated value of statexj.

Here,q(·)is a finite-level uniform quantizer,andg(·)＞0 is a scaling function.

The quantizerq(·)is a map fromRto the set of quantized levels Γ :={0,±1,···,±K}.In this paper,the associated quantizerq(·)is given by

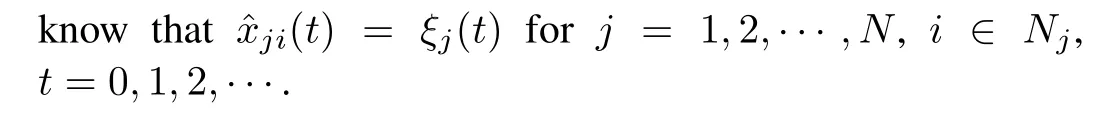
whereJ:=(1/N)11T.

Equations(4)and(5)can be respectively rewritten as

whereQ([y1,···,yN]T):=[q(y1),···,q(yN)]T.

Substituting(8),(9)and(6)into system(1)leads to

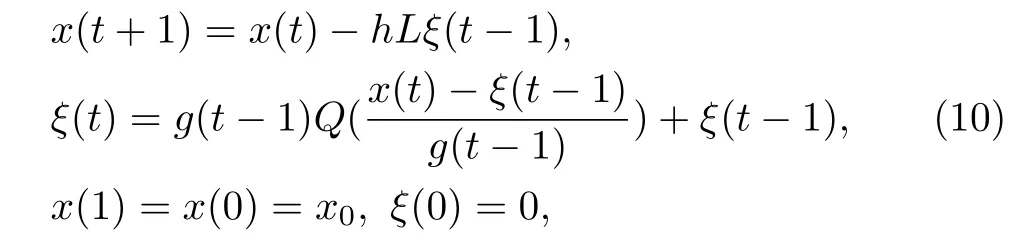
fort=1,2,···.

Note thatJL=0,we haveJx(t+1)=Jx(t).That is,

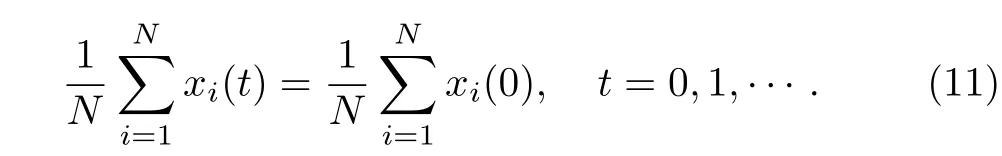
This means that the closed-loop system(10)preserves average value of the states.

III.MAIN RESULTS

For our mentioned multi-agent networks,we make the following assumptions.

Assumption 1.G=(V,E,A)is fixed undirected connected information exchange topology.

Assumption 2.|x0|∞≤C1,|δ0|∞≤C2,whereC1andC2are known nonnegative constants.

Remark 1.For Assumption 1,we have 0=λ1＜λ2≤···≤λN,whereλi:=λi(L)is the eigenvalue of the Laplacian matrixLofG[17].For Assumption 2,we accept Remark 6 in[5].That is,we have a good estimate with the initial states.

Lemma 1[5].If Assumption 1 holds and 0＜h＜2/λN,thenρh＜1,whereρh:=max2≤i≤N|1-hλi|.Furthermore,if 0＜h＜2/(λ2+λN),thenρh=1-hλ2.

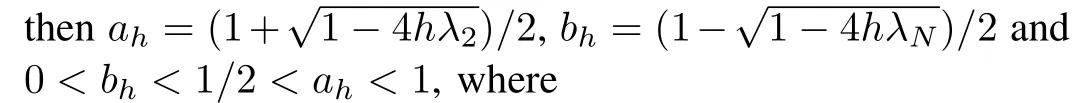
Proof.Note thatGis connected.It is easy to complete the proof,so we omit the details. □

Lemma 3.For any positive integerskandr,

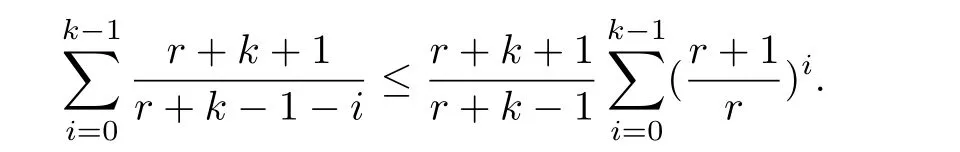
Proof.It is easy to complete the proof,so we omit the details. □

We prove that the network can achieve average consensus asymptotically with protocol(4).In Section III-A,we choose an inverse proportion function as scaling function.In Section III-B,we choose an exponential function as scaling function.

A.Distributed Protocol with an Inverse Proportion Function as Scaling Function

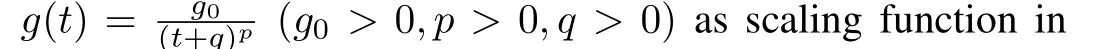
whereξij(t)∈Randˆxij(t)∈Rare the internal state of Φijand the output of Ψij,respectively[6].

Theorem 1.Suppose Assumptions 1 and 2 hold.For any givenh∈(0,1/(4λN)),integerr＞1/(1-ah),integerK≥「M1(h,r)⏋and

whereah,bhare given by Lemma 2 and

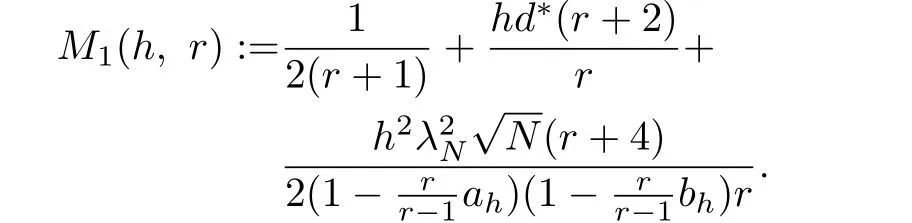
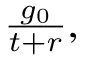
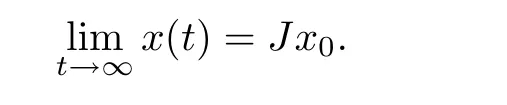
Proof.We chooseh,r,K,g0which satisfy the theorem′s conditions.

By(10)andLJ=JL=0,we have

Noting that

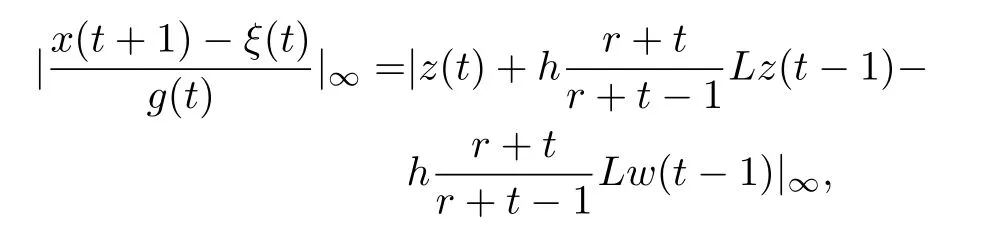
we only need to prove

Secondly,we assume that

Lastly,fort=k+1 we will prove

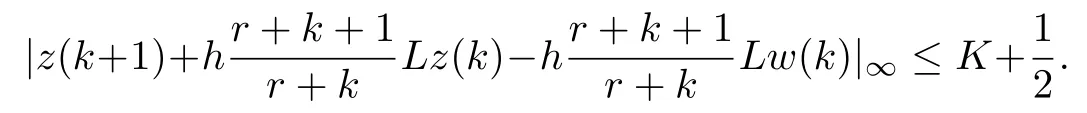
fort=2,3,···.

Now we estimate the three terms on the right-hand side of the above equation,separately.

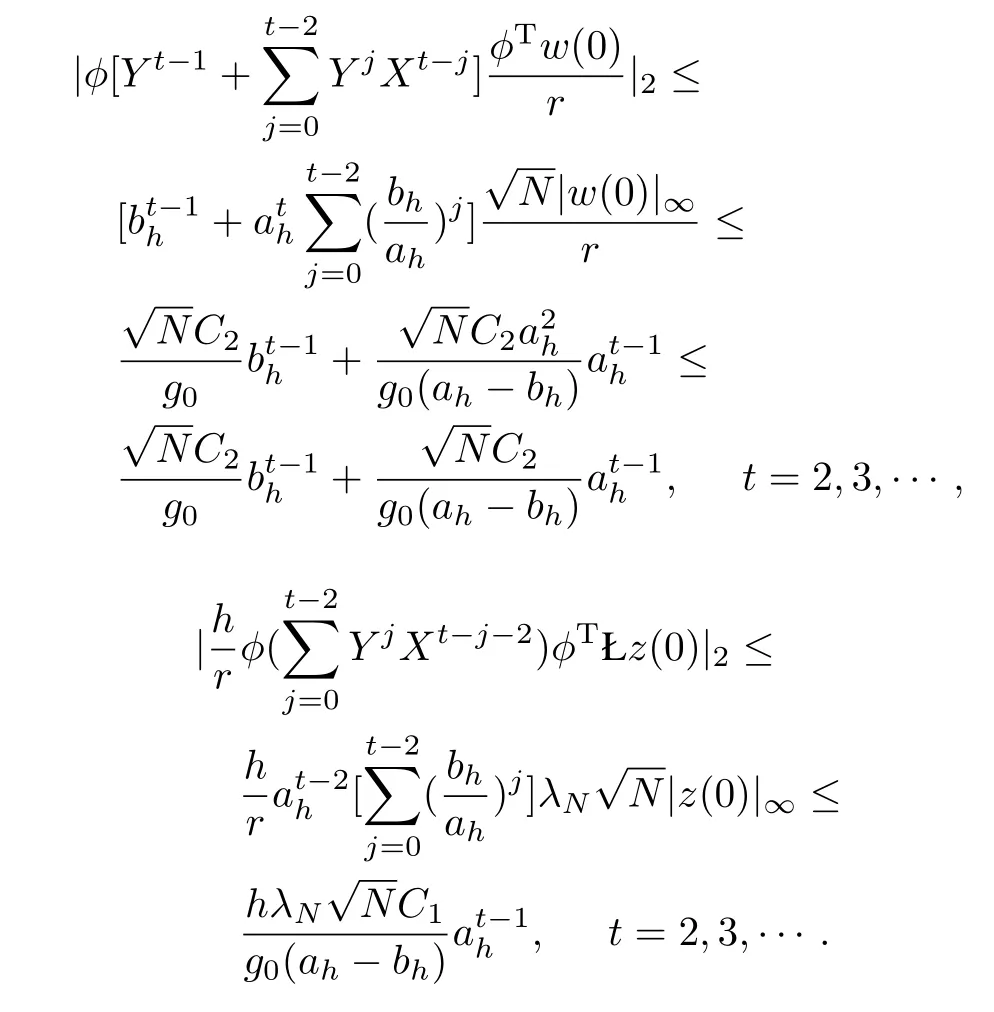
fort=3,4,···,k.So we have

By induction,we conclude that

fort=1,2,···.

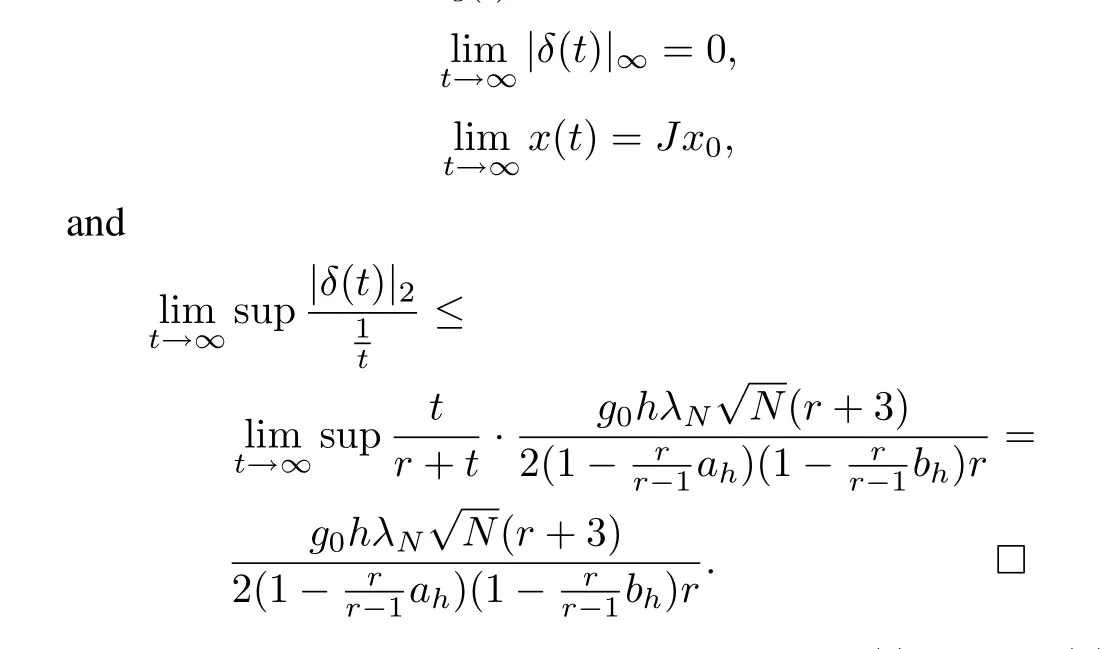
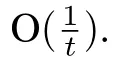
Under the protocol given by(3),(5)and(6),the closed-loop system can be written as

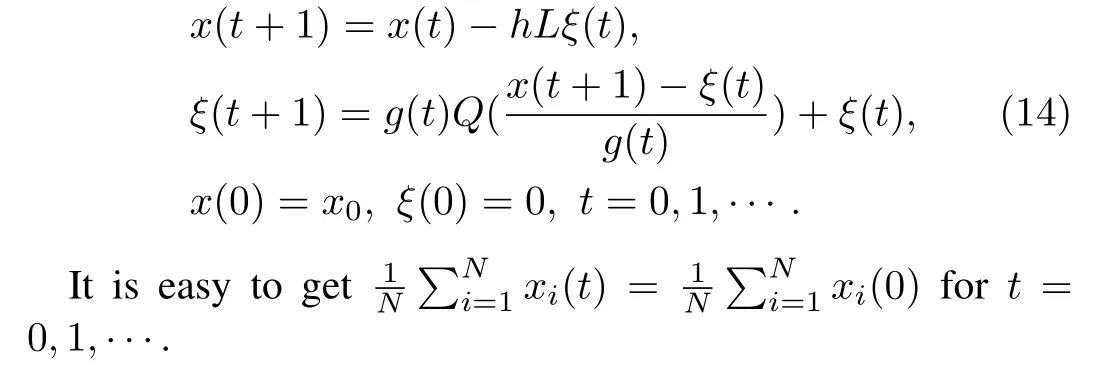
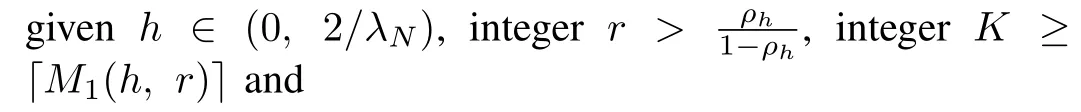
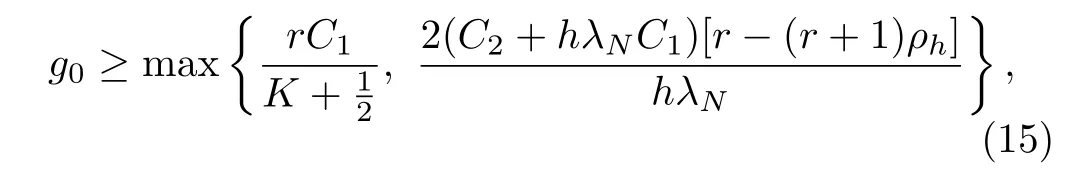
whereρhis given by Lemma 1 and

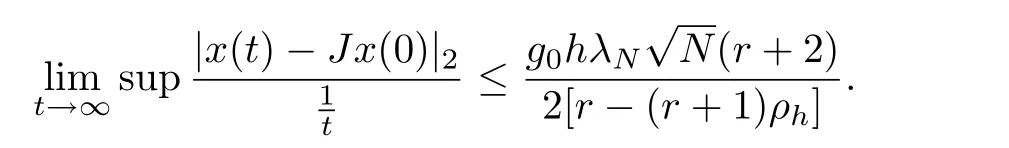
Proof.We chooseh,r,K,g0which satisfy theorem′s conditions.By(14),we have

fort=0,1,···.Specifically,we haveδ(1)=δ(0)=x0-Jx0,e(0)=x0.

The rest proof is similar to Theorem 1,so we omit the details. □

Remark 3.From the proofs of Theorems 1 and 2,we conclude that the multi-agent network can achieve average consensus asymptotically by using the following protocol

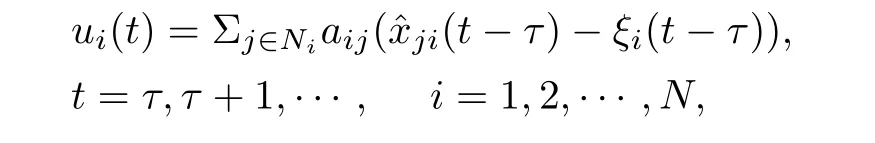
whereτis a nonnegative integer,h,r,Kandg0are appropriate parameters.That is,protocol(4)is robust to finite symmetric time-delays.Namely,we can chooseτas 0,1 or other positive integer.On the other hand,if the protocol changes into

then the multi-agent network will not achieve average consensus asymptotically(see Example 4).Therefore,the distributed average consensus problem of multi-agent digital networks has many challenges.

B.Distributed Protocol with an Exponential Function as Scaling Function

In this section,we chooseg(t)=g0rtas scaling function in encoders and decoders.

whereah,bhare given by Lemma 2 and

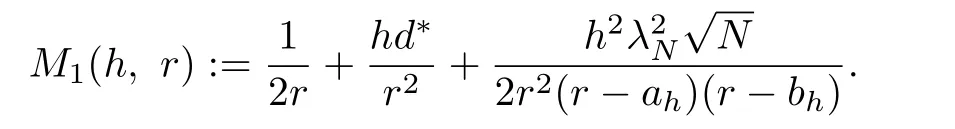
Then under the protocol given by(4)～(6)with the(2K+1)-level uniform quantizer(7)and the scaling functiong(t)=g0rt,the multi-agent network(1)can achieve average consensus asymptotically.That is,the closed-loop system(10)satisfies

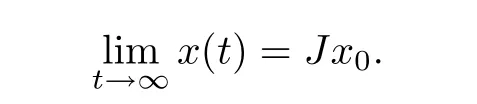
Furthermore,the convergence rate is at least O(rt).Actually,

Proof.The proof is similar to Theorem 1,so we will drop some details.We chooseh,r,Kandg0which satisfy the theorem′s conditions.

By(10),we have

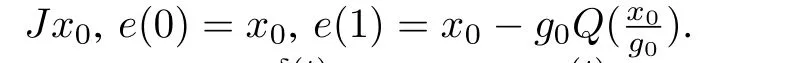
We only need to prove

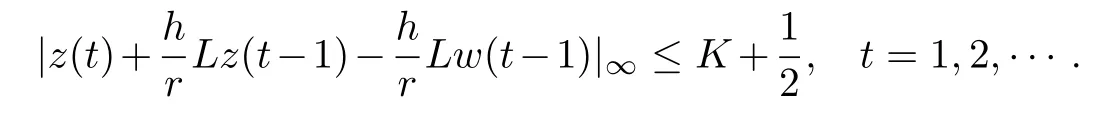
Secondly,we assume that

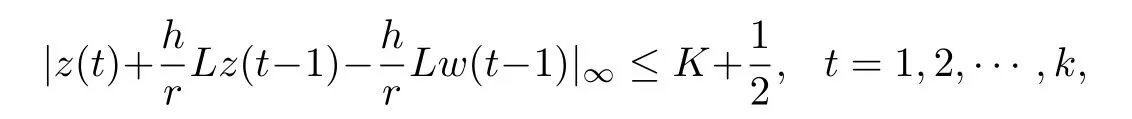
Lastly,fort=k+1 we will prove

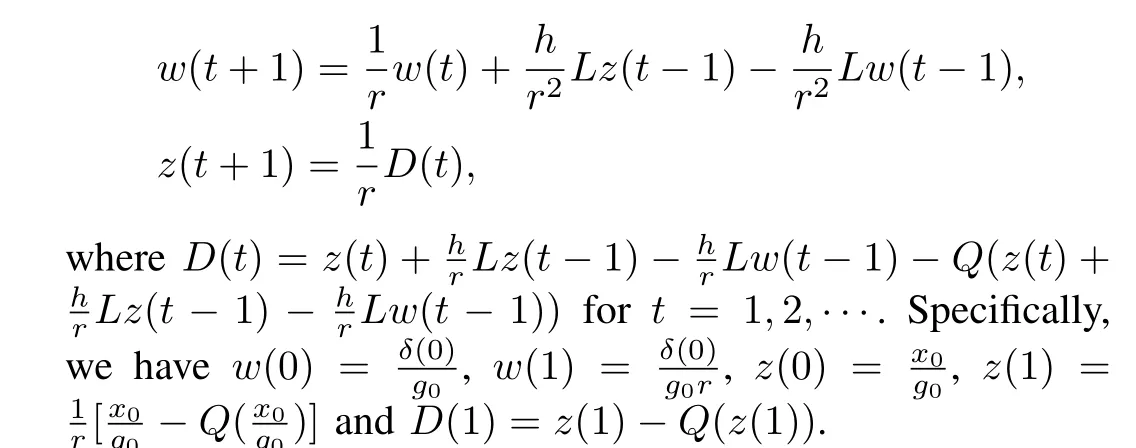
Noting thatˆw(t)=UTw(t)andˆw1(t)=0,ˆw2(t)=φTw(t),we have

fort=2,3,···.

Now we estimate the three terms on the right-hand side of the above equation,respectively.

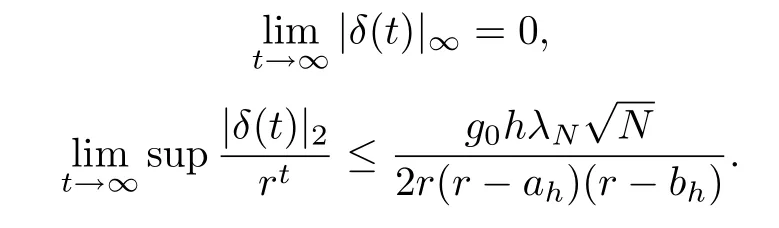
Remark 4.From Theorem 3,we havex(t)→Jx(0)ast→∞,and the convergence rate is at least O(rt)withr∈(ah,1).

Remark 5.Comparing these theorems,we have the followings conclusions.

1)We can always choose some feasible parametersh,r,Kandg0by these theorems,such that the multi-agent network can achieve average consensus asymptotically.

2)The scaling functions can influence the convergence rate.

3)For our mentioned multi-agent digital networks,the average consensus protocol(4)is robust to finite symmetric time-delays,but is sensitive to asymmetric time-delays.The asymmetric time-delays will destroy the average consensus.

IV.NUMERICAL EXAMPLES

We consider a network with 10 nodes.The interconnection topology is modeled as a simple undirected circuit graph and shown in Fig.1.Ais the adjacency matrix,

Based on the above conditions,we choose a set of control parameters to illustrate the above theorems.

Example 1.For Theorem 1,we chooseh=0.02,then we haveah=0.9923,bh=0.0877.And we chooser=185,K=5,g0=170.The evolution of the states is shown in Fig.2(a).We only changeg0=3,and get the evolution of the states which is shown in Fig.2(b).It can be seen that the average consensus is all achieved asymptotically.

Example 2.For Theorem 2,we chooseh=0.40,then we haveρh=0.8472.And we chooser=7,K=104,g0=4.5.The evolution of the states is shown in Fig.3(a).We only changeK=5,and get the evolution of the states,which is shown in Fig.3(b).It can be seen that the average consensus is all achieved asymptotically.

Example 3.For Theorem 3,we chooseh=0.02,then we haveah=0.9923,bh=0.0877.And letr=0.9950,K=5 andg0=1.The evolution of the states is shown in Fig.4(a).We only changeK=2,and get the evolution of the states which is shown in Fig.4(b).It can be seen that the average consensus is all achieved asymptotically.

Fig.1.The interconnection topology.

Fig.2. The trajectories of the states in Example 1.

Fig.3.The trajectories of the states in Example 2.

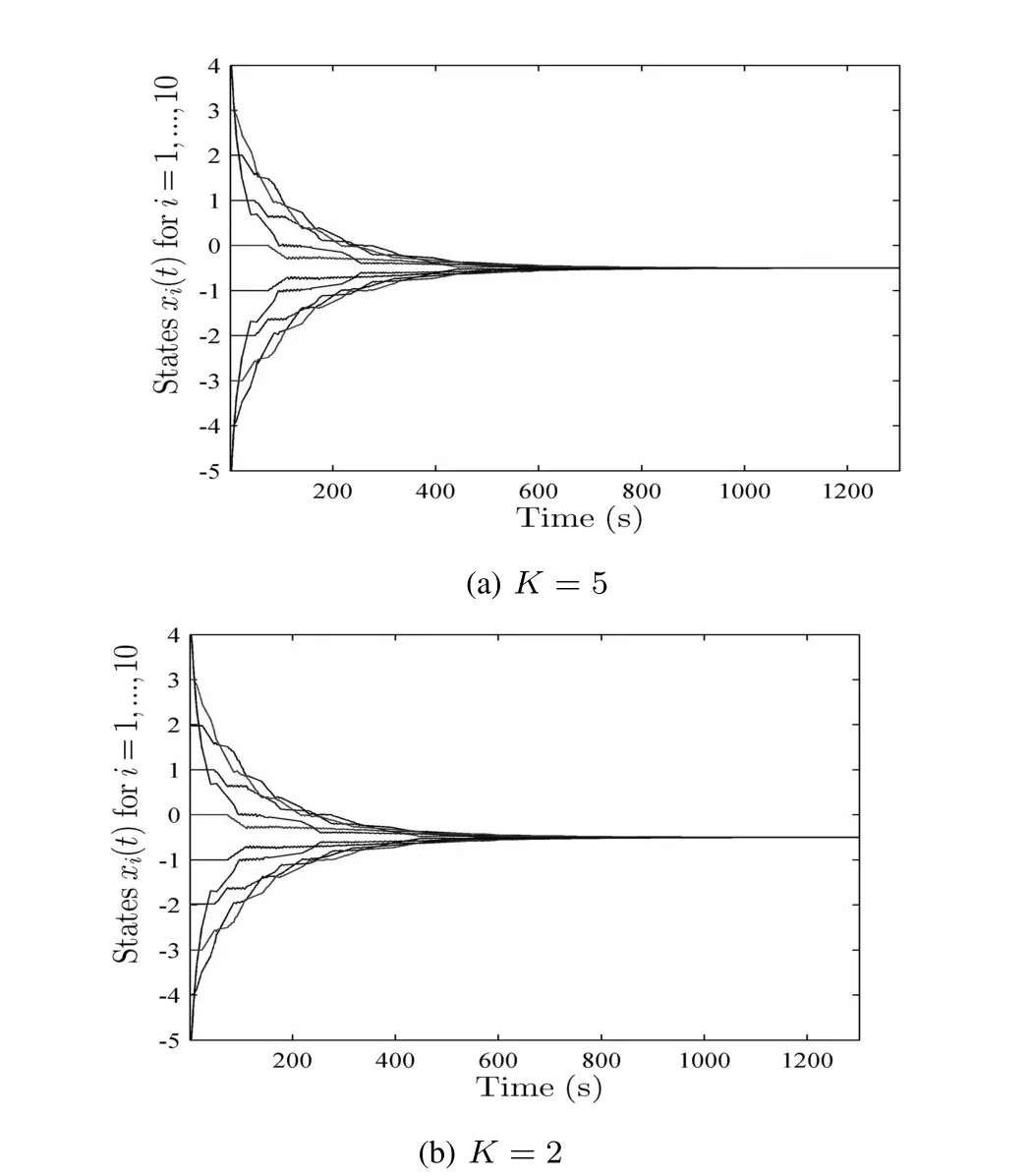
Fig.4.The trajectories of the states in Example 3.

V.CONCLUSION AND DISCUSSION

In this paper,the average consensus control problem has been considered for the undirected networks with finite bandwidth and time-delays.The average consensus problem can be efficiently solved by our protocol.Furthermore,we show that the average consensus protocol is robust to finite symmetric time-delays,but is sensitive to asymmetric time-delays.The asymmetric time-delays will destroy the average consensus of the networks.Meanwhile,we find that the theoretical results are still quite conservative from simulations.For future research,how to relax the selection of parameters and how to choose the best parameters will be considered.

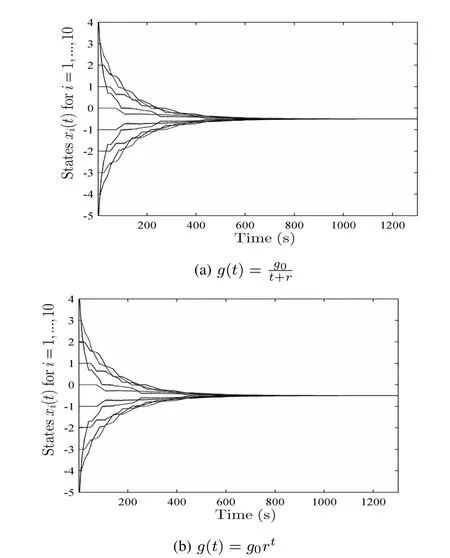
Fig.5.The trajectories of the states in Example 4.

APPENDIX

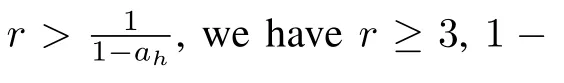
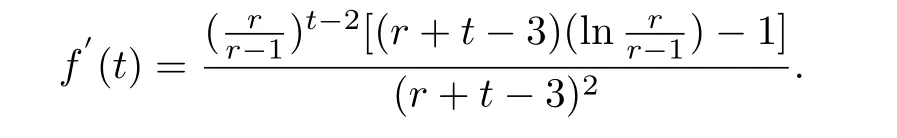
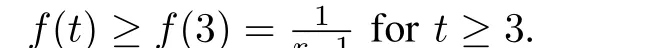
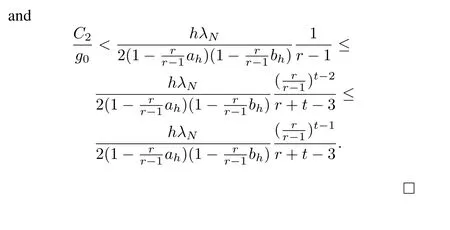
[1]Kashyap A,Bas¸ar T,Srikant R.Quantized consensus.Automatica,2007,43(7):1192-1203

[2]Carli R,Fagnani F,Frasca P,Zampieri S.Gossip consensus algorithms via quantized communication.Automatica,2010,46(1):70-80

[3]Cai K,Ishii H.Quantized consensus and averaging on gossip digraphs.IEEE Transactions on Automatic Control,2011,56(9):2087-2100

[4]Fang J,Li H B.Distributed consensus with quantized data via sequence averaging.IEEE Transactions on Signal Processing,2010,58(2):944-948

[5]Carli R,Fagnani F,Frasca P,Zampieri S.Efficient quantized techniques for consensus algorithms.In:NeCST workshop.Nancy,France,2007

[6]Frasca P,Carli R,Fagnani F,Zampieri S.Average consensus on networks with quantized communication.International Journal of Robust and Nonlinear Control,2009,19(16):1787-1816

[7]Carli R,Bullo F,Zampieri S.Quantized average consensus via dynamic coding/decoding schemes.International Journal of Robust and Nonlinear Control,2010,20(2):156-175

[8]Li T,Fu M Y,Xie L H,Zhang J F.Distributed consensus with limited communication data rate.IEEE Transactions on Automatic Control,2011,56(2):279-292

[9]Li T,Xie L H.Distributed consensus over digital networks with limited bandwidth and time-varying topologies.Automatica,2011,47(9):2006-2015

[10]Liu S,Li T,Xie L H.Distributed consensus for multi-agent systems with communication delays and limited data rate.SIAM Journal on Control and Optimization,2011,49(6):2239-2262

[11]Cheng Guan-Rong.Problems and challenges in control theory under complex dynamical network environments.Acta Automatica Sinica,2013,39(4):312-321(in Chinese)

[12]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533

[13]Carli R,Fagnani F,Speranzon A,Zampieri S.Communication constraints in the average consensus problem.Automatica,2008,44(3):671-684

[14]Min Hai-Bo,Liu Yuan,Wang Shi-Cheng,Sun Fu-Chun.An Overview on Coordination Control Problem of Multi-agent System.Acta Automatica Sinica,2012,38(10):1557-1570(in Chinese)

[15]Cao Xi-Bin,Guo Hai-Bo,Zhang Shi-Jie.Information topologyindependent consensus criteria for second-order systems under directed graph.Acta Automatica Sinica,2013,39(7):995-1002(in Chinese)

[16]Thanou D,Kokiopoulou E,Pu Y,Frossard P.Distributed average consensus with quantization refinement.IEEE Transactions on Signal Processing,2013,61(1):194-205

[17]Fiedler M.Algebraic connectivity of graphs.Czechoslovak Mathematical Journal,1973,23(2):298-305