A Continuous Leader-following Consensus Control Strategy for a Class of Uncertain Multi-agent Systems

Chuanrui Wang Xinghu Wang Haibo Ji

I.INTRODUCTION

OVER the last decade,cooperative control of multi-agent systems has attracted much attention from various disciplines.This is partially due to that it has many potential applications in many engineering systems,such as unmanned air vehicle,robotics,transportation and sensor networks.One fundamental problem in this area is the consensus problem,which contains the leader-less and leader-following consensus(or consensus tracking)problems.It aims to design distributed control laws using the relative information between neighboring agents such that the states or outputs of all agents reach an agreement[1-4].

Compared with the leader-less consensus problem,the leader-following consensus problem is more challenging and has more applications.With an active second-order leader agent,[5-6]studied the leader-following consensus problem of first-order and second-order multi-agent systems,respectively.Reference[7]investigated the second-order leader following consensus problem with multiple time-varying delays,where some necessary and(or)sufficient conditions were obtained for both fixed and switching topologies.In[8],the authors proposed discontinuous consensus tracking and swarm tracking algorithms for first-order or second-order multi-agent systems without velocity or acceleration measurements.Reference[9]proposed topology-independent consensus protocols for second-order multi-agent systems.References[10-12]investigated the leader-following consensus problem for multi-agent systems with general linear dynamics.

Note that most of the existing works focus on the consensus problem of linear multi-agent systems under the assumption that the exact model knowledge of the agent dynamics is known.However,in reality,all physical systems are inherently nonlinear and there may exist disturbances and unmodeled uncertainties.In the existing literature,there are few results on the robust consensus problem of uncertain nonlinear multi-agent systems.An attempt on this problem can be found in[13-14],where continuous robust consensus tracking control laws were constructed for a class of first-order and second-order integrator-type multi-agents systems,respectively.The proposed construction was based on the recently developed continuous nonlinear robust control technique called the robust integral of the sign of the error[15].The main advantage of this technique is that a continuous control law rather than a usually discontinuous control law can be constructed for a class of systems with bounded disturbances.Therefore,many results have recently been developed[16-18].

In this paper,we further study the leader-following consensus problem for a class of multi-agent systems with disturbances and unmodeled uncertainties.Contrary to[13-14],where only first-order and second-order integrator-type multi-agents systems were investigated,we consider a class of more general multi-agent systems.We firstly consider a linear single input multi-agent system in the controllable canonical form with disturbances and unmodeled uncertainties satisfying matching condition,which can be see as an extension of[15]to multi-agent systems.By employing the robust integral of the sign of the error technique,a continuous distributed control law is constructed which achieves semiglobal leader-following consensus.We then extend the above result to a class of multi-input multi-agent systems with disturbances and unmodeled uncertainties satisfying matching condition.Moreover,we show that if the unmodeled uncertainties vanish or satisfy global Lipschitz condition,then global leader-following consensus can be achieved.It is worth pointing out that different from some previous results such as[7,10-11],where the leader′s control input was assumed to be available to all follower agents,we consider a more general case,that is,the leader′s control input is nonzero and not available to any follower agent.Note that[5-6,8,12]have also studied this problem.However,they only considered the linear multi-agent systems cases.Moreover,the resulted closed-loop system solutions of[5-6]were only bounded with any positive constant while the proposed control laws in[8,12]were discontinuous.

II.PRELIMINARIES

LetG(V,E,A)be an undirected graph of orderN,whereV={1,2,···,N}is the set of nodes,E⊂V×Vis the set of undirected edges andA=[aij]N×Nis the adjacency matrix withaii=0.An edge denoted by pair(j,i)represents a communication channel fromjtoi.For undirected graphG,if(j,i)∈E,then(i,j)∈E.The neighborhood of thei-th agent is denoted byNi={j∈V|(j,i)∈E}.For anyi,j∈V,aij≥0 andaij＞0 if and only ifj∈Ni.The Laplacian matrix of graphGis defined asL=D-A,whereD=diag{d1,d2,···,dN}is called the degree matrix ofGwithdi=Pj∈Niaij,i=1,···,N.A path from nodei1to nodeikis a sequence of edges of the form(i1,i2),(i2,i3),···,(ik-1,ik),whereij∈V,j=1,···,k.If there exists a path between any two vertices ofG,thenGis said to be connected,otherwise disconnected.A subgraphG1ofGis an induced subgraph if two vertices ofG1are adjacent inG1only if they are adjacent inG.

Consider a graph¯Gconsisting ofNagents and a leader agent.When regarding theNagents as the vertices inV,the relationships between agents can be described by a simple and undirected graphG.(i,j)is an edge ofGif and only if agentsiandjare neighbors.¯GcontainsGand a leader with edges between some agents and the leader.The connection weight matrix is denoted byB=diag{b1,···,bN},wherebi≥0,i=1,···,Nandbi＞0 if and only if agentiis connected to the leader.¯Gis connected if at least one agent in each component is connected with the leader.DenoteH=L+B.A useful lemma aboutHis given as follows.

Lemma 1[5].If graph¯Gis connected,then the symmetric matrixHassociated with¯Gis positive definite.

III.PROBLEM STATEMENT

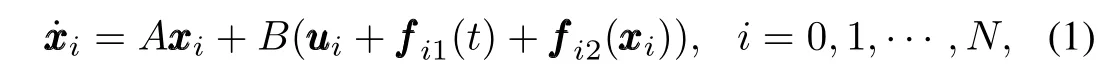
The objective of this paper is to solve the semiglobal leader-following consensus problem of system(1).

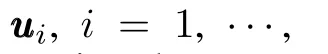
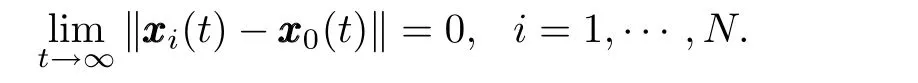
To facilitate the stability analysis,the following mild assumptions are given for system(1).

Assumption 1.(A,B)is stabilizable.

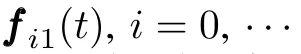
IV.MAIN RESULTS

In this section,we will design continuous distributed control laws to solve the semiglobal leader-following consensus problem for system(1)by employing the robust integral of the sign of the error technique.

A.Design of a Linear Single Input Uncertain Multi-agent Systems

Firstly,we consider a class of single input uncertain multi-agent systems that can be seen as a special case of system(1).The dynamics ofi-th agent is given by

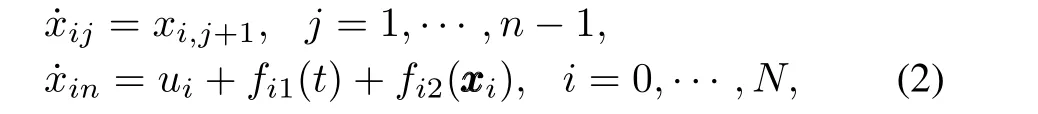
The relative state betweeni-th agent and its neighboring agents is defined as follows:

Its dynamics is described by

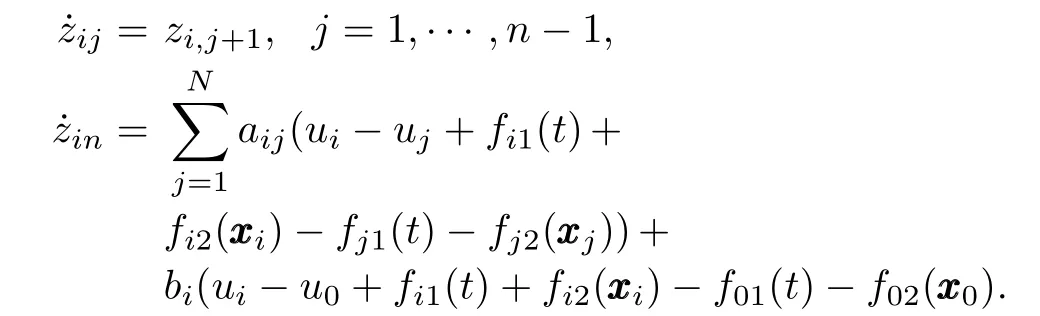
Define the filtered tracking errorri∈Ras follows:

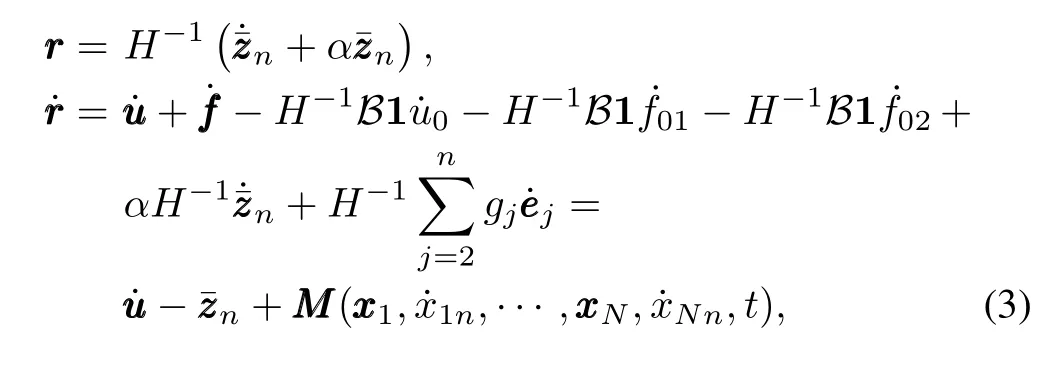
According to the mean value theorem,there exists a nondecreasing functionχsuch that the following holds

Based on the above analysis,we can now design a continuous distributed control law as follows:

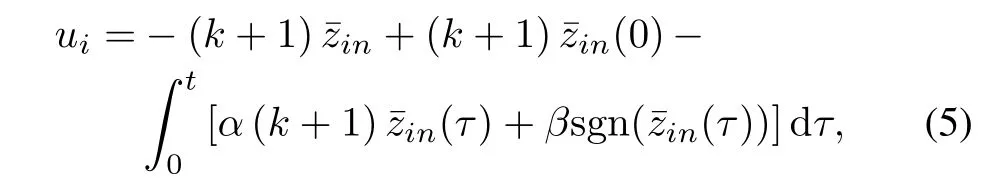
wherek,βare positive constants,and sgn(·)denotes the standard signum function.Then,we have

Lemma 2[14-15].Let the auxiliary functionL(t)∈Rbe defined as follows:

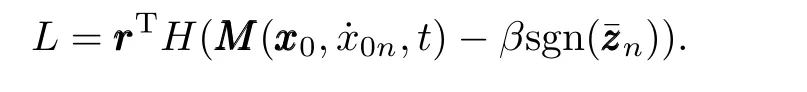
If positive constantβis selected to satisfy the following condition

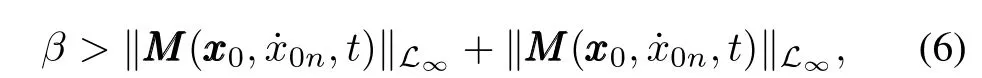
where‖·‖L∞denotes theL∞norm,then Z

Theorem 1.Consider system(2),and assume Assumptions 2～4 hold.The control law(5)solves the semiglobal leader-following consensus problem of system(2),provided that the control gainα＞αc＞0,βis selected according to inequality(6),andkis chosen sufficiently large,where positive constantαcwill be given in the following analysis.

Proof.DefineQ(t)=ϖ-Rt0L(τ)dτ∈R.By Lemma 2,Q(t)≥0 ifβis selected according to inequality(6).Consider the following Lyapunov candidate function

then there exists a positive constantγsuch that

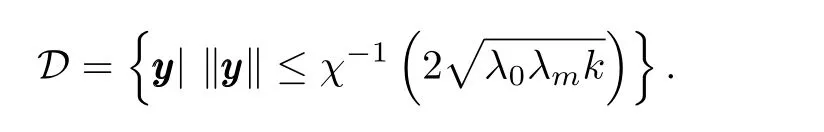
To show that the leader-following consensus problem is solved locally,consider the following region

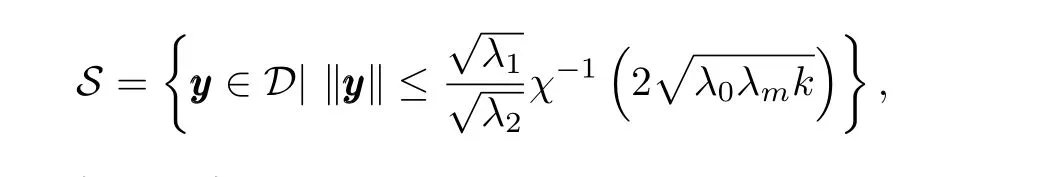
whereλ1andλ2are two positive constants such that

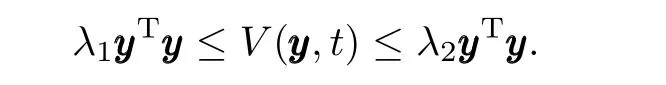
y(0)∈S.So,the leader-following consensus problem is solved locally by the distributed control law(5).Note that semiglobal leader-following consensus can be achieved by properly choosing the control gainkthat depends on the initial conditions. □

B.Design of General Linear Uncertain Multi-agent Systems

In this subsection,we study the semiglobal leader-following consensus problem of system(1)based on the last subsection.

Since(A,B)is stabilizable,by[20],there exists an invertible matrix Γ∈Rn,such that

where0′s represent zero matrices with compatible dimensions,Bi=[0,···,0,1]T,i=1,···,p,

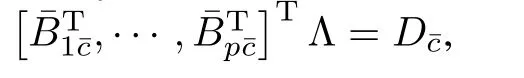
Dj¯c,j=1,···,pare some corresponding submatrices ofD¯c,andBj¯cnjdenotes the last row of matrixBj¯c.

To solve the semiglobal leader-following consensus problem of system(9),we next consider a class of multi-agent systems as follows:

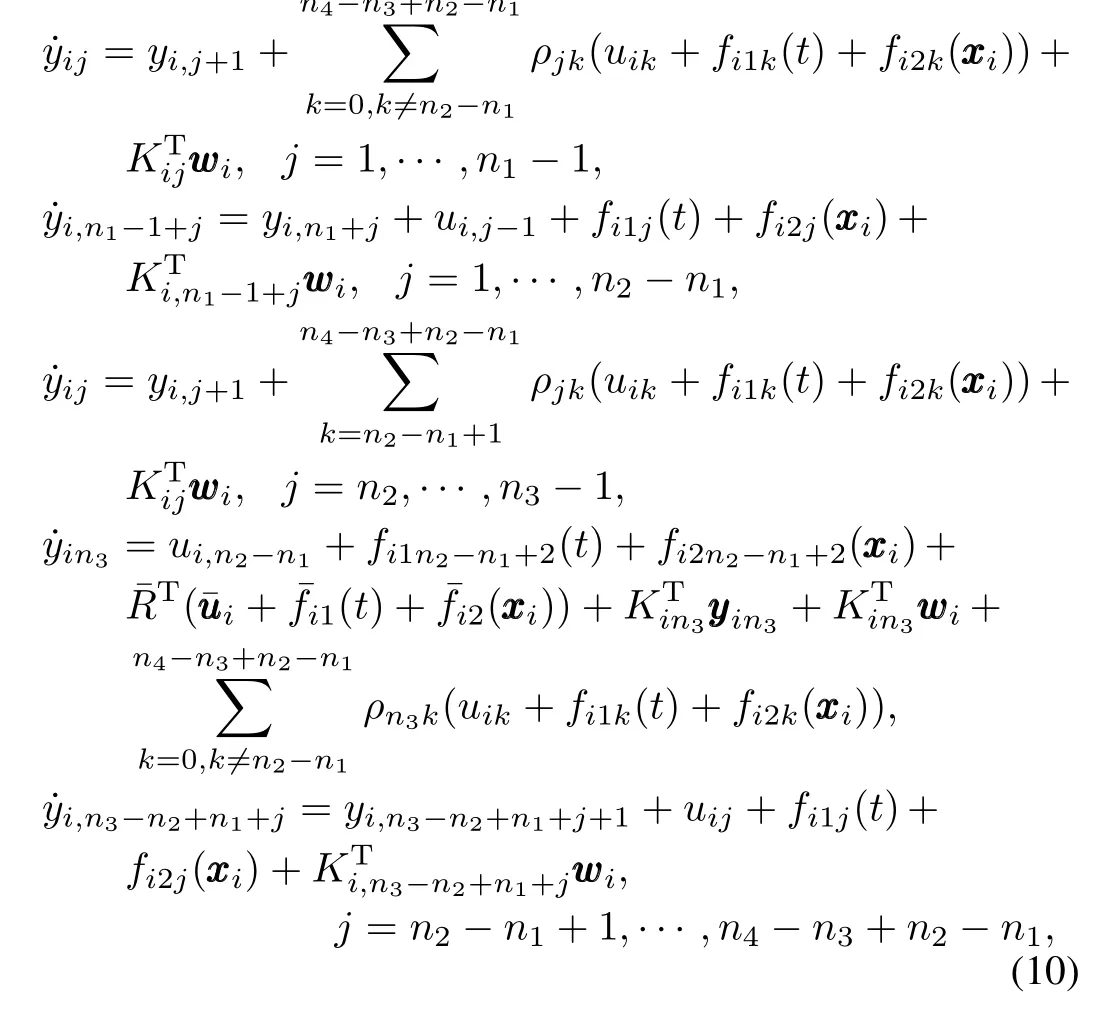
As in the last subsection,design distributed control laws similar to(5).Then,there exists a Lyapunov function¯Vin the form of(7)such that

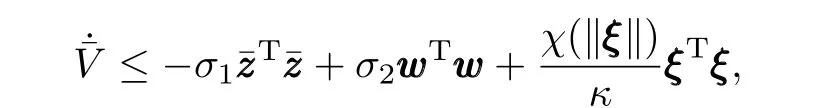
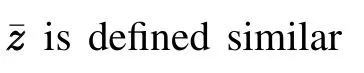
Consider the following Lyapunov candidate function for system(1),or equivalently,system(10)

ˇαj,j=1,···,p+1 are positive constants andP¯cis a positive definite matrix satisfying the following equation

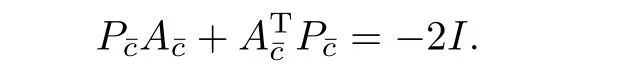
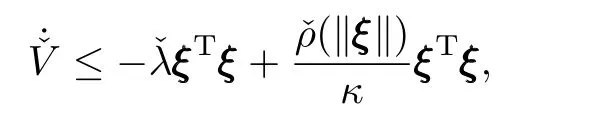
for a nondecreasing functionˆρand a positive constantˆλ.

By the proof of Theorem 1,we have the following result.

Theorem 2.Under Assumptions 1～4,there exists a continuous distributed control law that solves the semiglobal leader-following consensus problem of system(1).

Remark 3.It is worthwhile to mention two related works[8,12],which have studied the leader-following consensus problem with unknown but bounded input.Compared with those two papers,the contribution of our paper is at least twofold.First,we consider a class of more general systems with unknown nonlinear dynamics and unknown but disturbances.Second,the distributed control law developed in[8,12]are discontinuous,while in our paper,continuous distributed control laws are designed by employing the robust integral of the sign of the error technique.

V.SIMULATION RESULT S

Consider a multi-agent system with four followers labeled 1,2,3,4 and a leader labeled 0.The dynamics of thei-th agent is described by(1)with

The Laplacian matrix of the corresponding connected information exchange graphGis given by

and the leader adjacency matrix is given byB=diag{1,0,0,0}.

Consider the following state transformation

Note that system(11)are in the form of(10).Denote

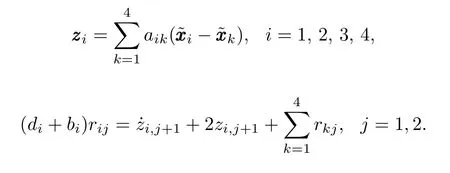
According to our design procedure,we construct the control lawsuijas follows:

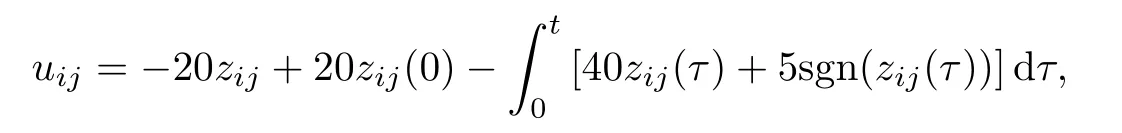
where we chooseα=2,β1=β2=5,andκ=20.The robust tracking results are depicted in Fig.1.It can be seen that the leader-following consensus is achieved.

Fig.1. Relative states zij,i=1,2,3,4,j=1,2,3.

VI.CONCLUSION

In this paper,we have considered the leader-following consensus problem for a class of uncertain multi-agent systems.Based on the relative state between neighboring agents,continuous distributed control laws have been designed by employing the robust integral of the sign of the error technique,which solve the semiglobal leader-following consensus problem.For future research,it is interesting to consider the leader-following consensus problem with only relative output between neighboring agents that are measurable.

[1]Jadbabaie A,Lin J,Morse A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988-1001

[2]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533

[3]Olfati-Saber R.Flocking for multi-agent dynamic systems:algorithms and theory.IEEE Transactions on Automatic Control,2006,51(3):401-420

[4]Ren W,Beard R.Distributed Consensus in Multi-Vehicle Cooperative Control.London:Springer-Verlag,2008

[5]Hong Y G,Hu J P,Gao L X.Tracking control for multi-agent consensus with an active leader and variable topology.Automatica,2006,42(7):1177-1182

[6]Gao L X,Zhu X J,Chen W H.Leader-following consensus problem with an accelerated motion leader.International Journal of Control,Automation,and Systems,2012,10(5):931-939

[7]Zhu W,Cheng D Z.Leader-following consensus of second-order agents with multiple time-varying delays.Automatica,2010,46(12):1994-1999

[8]Cao Y,Ren W.Distributed coordinated tracking with reduced interaction via a variable structure approach.IEEE Transactions on Automatic Control,2012,57(1):33-48

[9]Cao X B,Guo H B,Zhang S J.Information topology-independent consensus criteria for second-order systems under directed graph.Acta Automatica Sinica,2013,39(7):995-1002

[10]Ni W,Cheng D Z.Leader-following consensus of multi-agent systems under fixed and switching topologies.Systems and Control Letters,2010,59(3-4):209-217

[11]Zhang H W,Lewis F,Das A.Optimal design for synchronization of cooperative systems:state feedback,observer and output feedback.IEEE Transactions on Automatic Control,2011,56(8):1948-1952

[12]Li Z K,Liu X D,Ren W,Xie L H.Distributed tracking control for linear multi-agent systems with a leader of bounded unknown input.IEEE Transactions on Automatic Control,2013,58(2):518-523

[13]Hu G Q.Robust consensus tracking for an integrator-type multi-agent system with disturbances and unmodelled dynamics.International Journal of Control,2011,84(1):1-8

[14]Hu G Q.Robust consensus tracking of a class of second-order multi-agent dynamic systems.Systems and Control Letters,2012,61(1):134-142

[15]Xian B,Dawson D M,de Queiroz M S,Chen J.A continuous asymptotic tracking control strategy for uncertain nonlinear systems.IEEE Transactions on Automatic Control,2004,49(7):1206-1211

[16]Cai Z,de Queiron M S,Dawson D M.Robust adaptive asymptotic tracking of nonlinear systems with additive disturbance.IEEE Transactions on Automatic Control,2006,51(3):524-529

[17]Makkar C,Hu G,Sawyer W G,Dixon W E.Lyapunov-based tracking control in the presence of uncertain nonlinear parameterizable friction.IEEE Transactions on Automatic Control,2007,52(10):1988-1994

[18]Patre P M,Mackunis W,Kaiser K,Dixon W E.Asymptotic tracking for uncertain dynamic systems via a multilayer neural network feed forward and RISE feedback control structure.IEEE Transactions on Automatic Control,2008,53(9):2180-2185

[19]Khalil H K.Nonlinear Systems(3rd edition).New Jersey:Prentice-Hall,2000

[20]Chen C T.Linear System Theory and Design.New York:Holt,Rinehart and Winston,1984