机载分布式相干MIMO雷达的杂波谱分析
匡云连,陆军,胡光岷
(1.电子科技大学 通信与信息工程学院,成都 611731;2.中国电子科学研究院,北京 100041)
0 引 言
MIMO雷达是利用阵列信号处理技术,发射端由多个天线发射独立信号,接收端由多个天线接收回波的一种新体制雷达[1~5]。当前研究的MIMO雷达利用多个发射端发射相互正交的波形,接收端对接收的发射波形进行分离。相比于传统的相控阵雷达,MIMO雷达具有系统自由度高、探测视角广和布阵灵活等优点。杂波特性研究是机载MIMO雷达的一项重要的基础研究工作。王永良等人分析了发射离散频率编码信号时机载MIMO雷达的杂波特性[6~10]。Frank 等人研究了多径效应对机载MIMO雷达杂波自由度的影响[11,12]。Wang研究了发射任意波形时机载MIMO雷达杂波自由度的估计[13]。本研究主要考虑载频步进频率、杂波起伏、速度模糊等情况时杂波自由度的影响。
根据雷达天线位置的空间分布,MIMO雷达主要分为统计MIMO雷达和相干MIMO雷达[14]。统计MIMO雷达是双/多基地组网雷达的发展,相干MIMO雷达可以看成是相控阵雷达的发展。相干MIMO雷达天线阵列单元集中布阵,更易满足机载雷达小平台、多任务的设计需求,多载频信号容易产生和分离并能够实现发射信号正交性的要求。因此,所研究的对象就是多载频机载分布式相干MIMO雷达。
首先基于均匀线阵(ULA,uniform linear array)建立了机载分布式相干MIMO雷达的阵列几何模型,然后以多载频矩形脉冲信号为发射信号建立了杂波模型,并介绍了两种经典的杂波功率谱估计方法及杂波特征值数的估计规则,最后仿真分析了不同情形下的杂波功率谱及特征谱。出于简便,将机载分布式相干MIMO雷达简称为分布式系统。
1 分布式系统杂波模型
分布式系统阵列天线的几何关系,如图1所示。

图1 机载分布式相干MIMO雷达阵列几何模型
假设雷达平台沿X轴做直线运动。p为距离环上的第p个杂波散射单元,定义X轴为零方位角,对应的俯角和方位角分别是φ,θ;β是相对于阵列的视线角,v是平台速度,α是载机速度与视线方向的夹角,Φ是载机速度与阵列轴线之间的夹角。假设总共有M个发射阵元,N个接收阵元,K个脉冲时间周期。发射阵列单元间距为dt,接收阵列单元间距为dr,收发阵列单元均为全向。当收发阵元位置重合时,则收发并用。假设第1个天线单元为阵列的相位参考点,杂波处于阵列远场,在一个相干处理时间间隔内,忽略平台运动引起的角度变化。
对于分布式系统,采用多载频矩形脉冲信号,则第m个发射阵元的视频信号可以写成:
Sm(t)=rect(t/Te)exp[j2π(m-1)Δft]
(1)
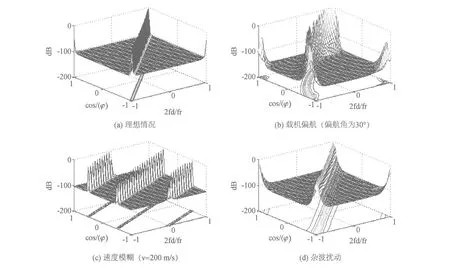
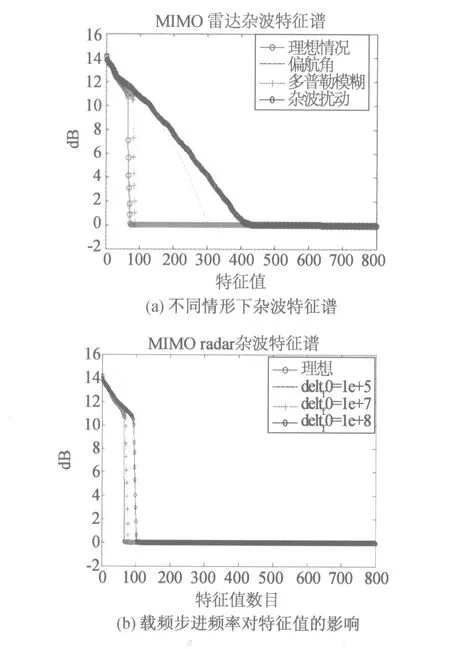
式中,rect(t)为门控信号,0 发射信号间的互相关为 (2) τm、τn分别为第m、n个发射单元发射信号的时间延迟。为了满足发射信号间的正交性,应满足式(2)为零,则有ΔfTe=k(k为整数)。假设杂波源的统计特性在空间上相互独立,在时间上相关平稳分布,则在第k个脉冲时间周期内,第n个阵元接收第l个距离环上散射单元的回波信号经匹配滤波器之后的输出为 (3) 式中,Nc为第l个距离环上杂波单元的个数;σcp为第p个杂波散射单元的雷达截面积;r0为阵列参考单元到P点的距离;Tr为雷达脉冲重复周期;vr=vcosα为雷达平台速度在视线方向的分量;λ为雷达工作波长。 ψ(Δf)=e-j4π(m-1)Δfr0 /ce-j2π(m-1)kΔfTr ej2π(m-1)Δf/c[(n-1)drcos β+(m-1)dtcos β +2(k-1)vr Tr ]为步进频率引起的相位差,忽略载频差异对接收阵列和多普勒频率的影响。对式(3)进行参考阵元初始相位的补偿并化简得到 (4) asw=[1,ej2πΔfdtcos β/c,…,ej2π(m-1)Δf(m-1)dtcos β/c]T (5) []T为向量的转置。定义发射空间导向矢量和接收空间导向矢量为 ast(β)=[1,ej2π/λdtcos β,…,ej2π/λ(m-1)dtcos β]T (6) asr(β)=[1,ej2π/λdrcos β,…,ej2π/λ(n-1)drcos βr]T (7) 定义时间导向矢量为 at(fd)=[1,ejfdTr,…,ejfd(k-1)Tr]T (8) (9) 定义 asd(β,fd)=[asw⊙ast(β)]⊗asr(β)⊗at(fd) (10) ⊙为HAdamard积,⊗为Kronecker积。asd为NMK×1维的杂波空时二维导向矢量,决定了杂波的空时二维特性。假设雷达接收机产生的噪声在时间和空间上不相关,回波信号可以写成 y=ycl+n (11) n为高斯白噪声,其协方差矩阵为 R=E{y*yH}=Rc+σ2I (12) 通过用一个导向矢量乘以杂波加噪声的估计的协方差矩阵或其逆,可以获得功率谱,功率谱反映了各频率成分的平均功率的大小及各频率成分的构成情况。功率谱具有两种经典的形式:傅里叶谱和最小方差谱。最小方差谱具有高分辨特性,非常接近真实的杂波模型,本文采用最小方差谱对杂波的空时特性进行估计。其表达式为 Pmv(β,fd)=[aHsd(β,fd)R-1asd(β,fd)]-1 (13) 特征谱实质上指的是杂波加噪声协方差矩阵的特征值分布,它反映了杂波处理所需要的自由度。在理想情况下,侧视线阵相控阵雷达的杂波特征值数的估计规则为[15] Nph≈int{N+(K-1)γ} (14) 式中,int表示下一个整数;γ=2vrTr/dr是空-时平面杂波轨迹的斜率。机载MIMO雷达杂波特征值数估计规则为[11] Nmimo≈int[N+κ(M-1)+γ(K-1)] (15) κ=dt/dr。考虑步进频率对杂波自由度的影响,对式(15)稍作修改 Nrank≈int{N+κ[(M-1)+(M-1)2λΔf/c]+γ(K-1)} (16) 从式(16)中看到杂波自由度与载频、步进频率,收发阵列单元数、脉冲时间间隔个数及收发间距之比等因素有关。 相控阵雷达系统自由度为N*K,定义其杂波相对自由度为Nph/(N*K),机载MIMO雷达的系统自由度为N*M*K,定义其杂波相对自由度为Nmimo/(N*M*K),则有 Nph/(N*K)-Nmimo/(N*M*K)≥0 (17) 机载MIMO雷达的杂波子空间增大了,但是杂波处理的维数占总的系统维数的比值减少了,这意味着机载MIMO雷达可利用更多的自由度进行信号处理。 依据分布式系统的阵列几何模型和杂波模型,仿真假设载机以100 m/s的速度沿x轴正方向做匀速直线运动,载机高度为8 km。发射阵元数为10,接收阵元数为5,收发阵元间距比为5,时间域相干处理脉冲数为16。 理想条件、载机速度与阵列轴线的夹角为30°、载机速度为200 m/s和杂波起伏情况下,MV杂波谱的变化曲线,如图2所示。由仿真结果可以看出,在理想情况下多载频分布式系统的杂波沿空时对角线均匀分布;当载机速度与阵列轴线存在夹角时,MV杂波谱发生弯曲,多普勒频率具有距离依从性,而且杂波谱变宽;载机速度为200 m/s时存在速度模糊,MV杂波谱会在“原谱”的两侧有模糊的杂波响应,杂波谱在多普勒域上有重叠;杂波起伏使得MV杂波谱展宽。 载频步进频率对MV杂波谱的影响,如图3所示。步进频率的增大使得MV杂波谱展宽,但是不改变正交性,能量仍均匀的分布在对角平面上。 图2 不同因素对MV杂波谱的影响 图3 步进频率对MV杂波谱的影响 针对图2中的杂波分布情况,进行了杂波特征谱的分析,如图4所示。理论计算得到的分布式系统的杂波特征值为65。从图4(a)中可以看出,理想情况下,分布式系统杂波的特征值与理论值基本相符,并具有明显的捷变特性。载机偏航、多普勒模糊和杂波起伏等因素都会导致杂波自由度偏大,这与图2杂波谱的展宽相对应,反映了杂波抑制滤波器的复杂性增加。从图4(b)中看到,载频步进频率使杂波自由度有轻微的增大。 图4 杂波特征值分布 从机载分布式相干MIMO雷达的阵列几何模型出发,建立了杂波模型,比较了机载相控阵雷达和机载分布式相干MIMO雷达的杂波自由度分布。仿真和分析结果得出在理想情况下机载分布式相干MIMO雷达具有斜对角空时二维特性,且在全方向均匀分布。杂波起伏、载机偏航均使杂波谱展宽,且载机偏航还会使杂波谱发生弯曲,载机速度增大引起杂波多普勒模糊;在满足正交条件时,载频的步进频率增大会导致多载频机载分布式相干MIMO雷达杂波谱扩展。 [1] ALEXANDER M.MIMO Radar with Widely Separated Antennas[J].IEEE Signal Processing Magazine,2008,25(1):116-129. [2] BLISS D W.Multiple-Input Multiple-Out(MIMO)Radar and Imaging:Degrees of Freedom and Resolution[J].IEEE,2003:54-59. [3] Fishler.E.MIMO radar:an idea whose time has come[C].IEEE,2004:71-78. [4] DONNET B J.MIMO Radar,Techniques and Opportunities[C]//proceedings of the 3rd European radar Conference,2006:12-115. [5] FRANK C.MIMO radar theory and experimental results[C].IEEE,2004:300-304. [6] 张西川,张永顺,谢文冲,等.波形正交性退化下机载MIMO雷达杂波模型与自由度分析[J].系统工程与电子技术,2012,34(1):80-84. [7] WANG YONG LIANG.General Clutter Modeling for Airborne Radar[C]//CSP2010 proceedings,2010:2 274-2 278. [8] 张西川,张永顺,谢文冲.机载相干MIMO雷达杂波自由度估计研究[J].电子与信息学报,2011,33(9):2 125-2 131. [9] 张西川,张永顺,王永良.机载MIMO雷达空时二维杂波建模及特性分析[J].空军工程大学学报,2010,11(5):35-38. [10] 严韬,谢文冲,王永良.机载MIMO雷达杂波建模及杂波特性分析[J].雷达科学与技术,2010,8(4):289-295. [11] MECCA V F,JEFFREY L.KROLIK.MIMO Enabled Multipath Clutter Rank Estimation[C].IEEE,2009. [12] MECCA V F.MIMO Radar Space-Time Adaptive Processing for Multipath Clutter Mitigation[C]//IEEE,2006:249-253. [13] WANG GUO HUA.Clutter Rank of STAP in MIMO Radar with Waveform Diversity[J].IEEE transaction on signal processing.2010,58(2):938-943. [14] LI J,PETER S.MIMO Radar Signal Processing[M].Hoboken:New Jersey,John wiley &Sons,Inc,2009. [15] KLEMM R.空时自适应处理原理[M].北京:高等教育出版社,2009.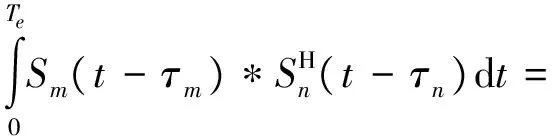
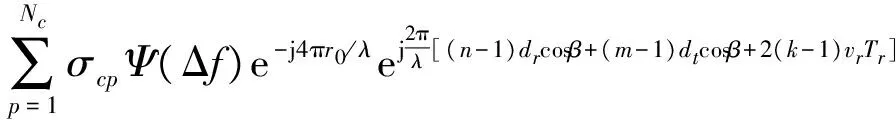
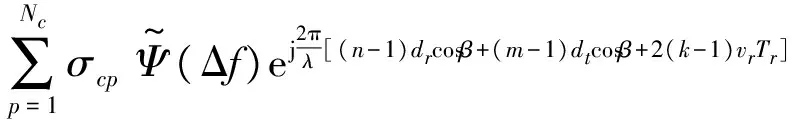


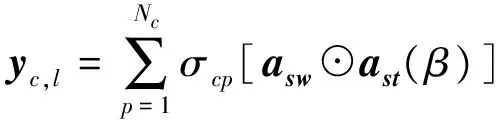
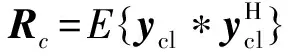
2 杂波谱分析
2.1 功率谱
2.2 特征谱
3 机载分布式相干MIMO雷达杂波谱仿真分析

4 结 语

