高温后混凝土断裂能的确定
商兴艳,俞可权,陆洲导
(同济大学 土木工程学院,上海,200092)
高温后混凝土断裂能的确定
商兴艳,俞可权,陆洲导
(同济大学 土木工程学院,上海,200092)
采用楔入劈拉法对高温后混凝土试件的断裂能GF进行测试,试验设置20~600 ℃内共10个温度段。对试验得到的荷载−开口位移曲线进行尾部曲线拟合。结果表明:当温度不超过120 ℃时,采用幂函数拟合更为准确;而当温度超过120 ℃时,采用指数函数拟合更为准确。由荷−开口位移曲线计算各温度下混凝土试件的断裂能GF,稳定断裂能GFS及失稳断裂能GFU,随温度的变化趋势均为保持不变—上升—下降,表明高温后混凝土断裂性能随温度呈现保持不变—上升—下降的趋势。
楔入劈拉法;高温;混凝土;曲线拟合;断裂能
混凝土断裂能GF定义为产生单位面积裂缝所需消耗的平均能量,表征了混凝土材料抵抗裂缝开展的能力。断裂能作为混凝土非线性断裂力学模型的基础,是断裂本构关系中必不可少的物理量。另一方面,随着非线性断裂理论的不断发展和成熟,该理论已被越来越多地引入到混凝土结构的计算、分析和设计中。混凝土非线性断裂理论的应用必须以断裂能参数已知作为前提条件。常温下众多学者对断裂能的测试方法[1−3]和尺寸效应[4−6]进行了深入分析,而高温作用后混凝土断裂能的研究较少。Bazant等[7]采用三点弯曲梁混凝土试件进行了高温中的断裂试验,发现混凝土I型断裂能随着温度的上升而单调下降。相反的,Baker等[8−9]的研究结果表明:在温度达到300 ℃前,高温后混凝土断裂能随温度上升而增加,随后断裂能迅速下降。Nielsen等[10]对普通混凝土和高性能混凝土在高温后的断裂能也进行了研究,得到与Zhang等[9]相同的结论。断裂能上升的主要原因是混凝土经历高温后出现较多的微裂缝,微裂缝在断裂过程中吸收能量,从而使得测定的断裂能偏高,同时混凝土试件体现出较大的延性。在国内,Peng等[11]研究了普通强度高性能混凝土和高强度高性能混凝土的高温后残余断裂能。现阶段,高温后断裂性能的研究均采用三点弯曲梁,三点弯曲梁试件体积大,升温控制较难,而楔入劈拉试件体积小,升温易控制,较之三点弯曲梁试件具有更大体积韧带比;另外,对断裂能的研究多停留在整体断裂能的求解,没有更进一步细化分析。本文作者采用楔入劈拉法测试高温后混凝土试件的断裂能,测得各试件荷载−开口位移曲线并对尾部曲线拟合处理,计算各温度下试件的断裂能及其随温度的变化趋势;在此基础上进一步将断裂过程分为稳定断裂阶段和失稳断裂阶段,得到了稳定断裂能与失稳断裂能随温度的变化趋势,从而更为细致的评判混凝土断裂性能随温度的变化规律。
1 试验概况
试验中试件长×宽×高均为230 mm×200 mm×200 mm,预制开口裂缝高80 mm,厚3 mm,试件几何形式见图1(图中,b=200 mm,d=65 mm,h=200 mm,f=30 mm,a0=80 mm,θ=15°)。试件混凝土配合比为m(水泥):m(砂):m(石子):m(水)=1:3.44:4.39:0.8,其中水泥采用海螺牌P.O42.5普通硅酸盐水泥,粗骨料最大粒径为16 mm,细骨料采用粒径为0.25~0.5 mm的中砂,标准配合强度为C30。每个试件内均插有热电偶,其位于预制裂缝附近,深入试件深度为100 mm,以便测得试件中心温度。试件洒水自然养护60 d。考虑到混凝土本身固有的离散性以及试件将经受高温作用,每组温度设有5个试件。
混凝土试块历经65,120,200,300,350,400,450,500和600 ℃高温,当试件达到设计温度时,关闭电炉。试件加热至65,300,450和600 ℃的平均耗时分别为50,182,294和453 min。试件自然冷却后采用塑料袋密封减少环境湿气渗入。
楔入劈拉法试验在1 000 kN的电液伺服万能试验机上进行,利用动静态数据采集系统进行试验数据采集。在预制裂缝开口和尖端处分别安装量程为4 mm的夹式引伸计,以测得试件的裂缝口开口位移和裂缝尖端开口位移。控制试验机加载速率为0.4 mm/min,保证试验得到稳定的荷载−裂缝开口位移曲线。对于温度低于200 ℃的试件,加载时间平均为15 min;温度高于400 ℃的试件,其加载时间平均达到40 min,主要表现为试件在荷载−开口位移曲线下降段所经历的时间较长。
图2所示为各温度下典型试件的荷载−开口位移曲线。可见:随着温度的上升,峰值荷载Pu明显下降,而对应的荷载−开口位移则显著上升。当温度由低到高变化时,荷载−开口位移曲线上升与下降段斜率明显由陡逐渐变缓。常温下试件劈裂面更为平整,而高温后试件劈裂面较为曲折。
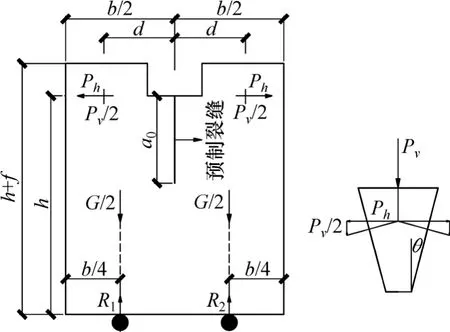
图1 试件几何形式Fig. 1 Geometry of specimens
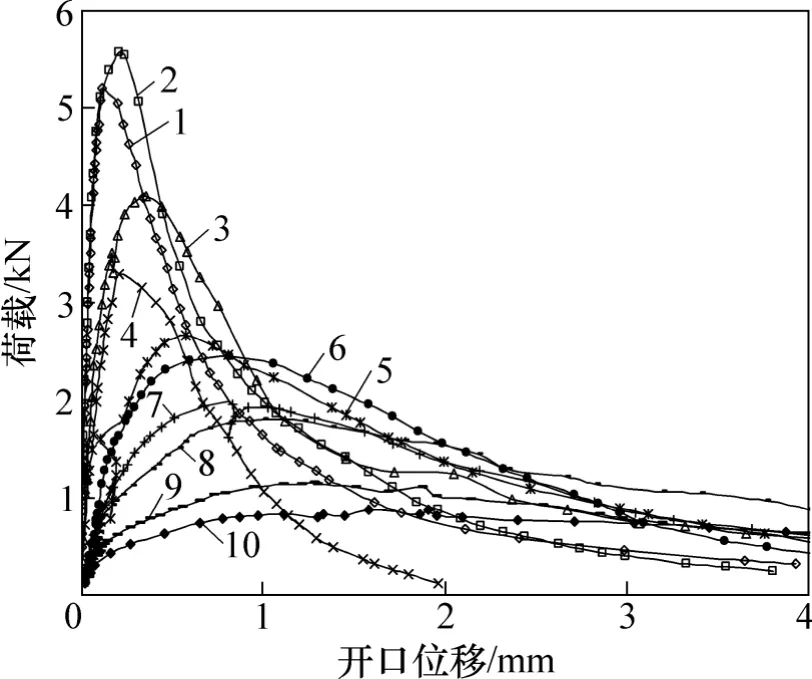
图2 各温度下典型试件的荷载−开口位移曲线Fig. 2 Load vs crack mouth opening displacement curves of specimens with temperatures
2 断裂能计算及趋势分析
断裂能GF是产生单位面积裂缝所需消耗的平均能量,并定义平行于主裂缝方向平面中的投影面积为裂缝面积。对于楔入劈拉试件,裂缝形成的能量全部为外荷载提供,荷载−开口位移全曲线所包围的面积就是外荷载的断裂功W;通常试件完全断裂,可取裂缝面面积为韧带面积。
当试验行将结束时,荷载下降速度非常缓慢,曲线十分平缓,为提高试验效率,只能在荷载基本接近于0 kN时结束试验,此时水平向荷载和裂缝开口位移分别为PH1和δ1,图3所示为考虑尾部曲线拟合的断裂能计算简图。断裂能GF计算公式为:
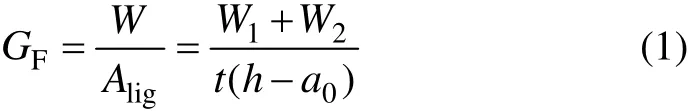
式中:W1为试验采集到荷载−位移曲线的包络面积;W2为考虑尾部曲线拟合的包络面积;Alig为试件韧带面积;t为试件厚度;h为试件高度;a0为试件预制裂缝高度。

图3 高温后试件尾部曲线拟合Fig. 3 Curve fitting results for post-fire specimens
本文试验采用反向加载,即加载过程中试验机底座上升,上夹头保持不动,所以整个过程中加载架自重已经计算在外力中,式(1)中不包括加载架自重mg。
对结束点之后尾部曲线引起的断裂能采取拟合数据的方法。多数试验表明,曲线下降段反弯点之后的部分呈一定的规律性。采用幂函数和指数函数[12−13]的形式对荷载−开口位移曲线进行拟合,并依据此拟合曲线计算试验结束点后的曲线面积W2。拟合结果表明,在20~120 ℃时,采用幂函数得到的拟合曲线相关系数R2更高;而当温度进一步提高时,采用指数函数得到的拟合曲线相关系数R2更高。各温度下典型拟合结果见图3所示。各温度下荷载−开口位移曲线的尾部曲线经适当拟合之后,便可计算曲线与坐标轴围合面积,即断裂功W,继而可求得断裂能GF。
图3中W1可以按照数值积分法求得。对于W2,当采用幂函数形式对尾部曲线进行拟合时,根据公式Ph=βδ-λ,断裂功为
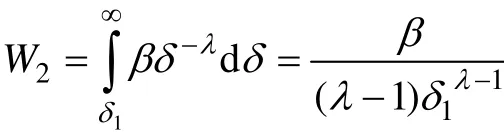
当采用指数函数形式对尾部曲线进行拟合时,根据公式:Ph=me−nδ,断裂功为
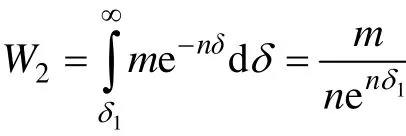
式中,β,λ,m,n为曲线参数,β,λ>0;δ为开口位移。
根据上述公式可计算各温度下试件破坏所需的总断裂功W以及断裂能GF。各温度下试件断裂功和断裂能计算结果见表1所示。
图4所示为断裂能与温度的关系。可见:随温度升高,断裂能变化趋势为保持不变−上升−下降:当温度低于120 ℃时,试件断裂能没有明显变化,略有升高;当温度在120~450 ℃时,混凝土内部生成较多的细微裂缝,这些裂缝在加载过程中同样消耗能量,使得断裂能随温度的增长而上升;当温度在450~600 ℃时,试件本身损伤加大,细微裂缝增多,但缝宽变大,混凝土试件抵抗裂缝的能力随温度升高而下降。由断裂能的变化趋势可以得到高温后混凝土断裂性能的变化趋势也为保持不变−上升−下降。
当温度由常温上升到450 ℃时,混凝土试件的平均断裂能由339.3 N/m上升到609 N/m,而当温度继续上升至600 ℃时,平均断裂能则降为307.8 N/m。
由于混凝土强度、材料组成(包括混凝土配合比、骨料直径等)、升降温制度以及试件几何形状的不同,本文的试验结果与文献[8−11]在具体数值上并无可比性,但是在整体趋势上,与文献均可以较好吻合。本文中高温后试件的断裂能在450 ℃时发生转折,与文献十分接近,表明各类混凝土断裂性能在发生转折时的温度比较接近。450 ℃发生突变的原因为水泥水化产物氢氧化钙在该温度开始分解,从而导致混凝土微观结构产生较大变化。

表1 各温度下断裂能计算结果Table 1 Residual fracture energy GF
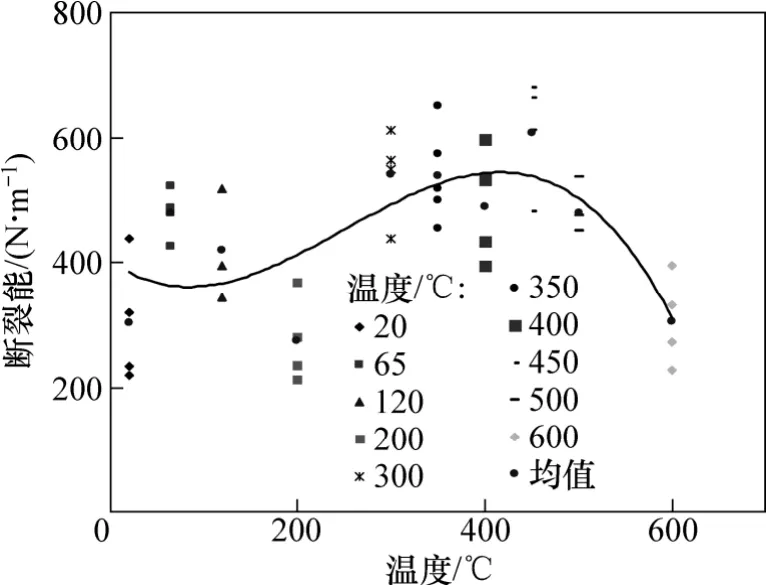
图4 断裂能与温度的关系Fig. 4 Relationship between GF and T
3 稳定断裂能与失稳断裂能
将断裂过程分为裂缝的稳定断裂阶段和失稳断裂阶段[14],相应的断裂能分别记为GFS和GFU。根据文献[14],稳定断裂阶段为裂缝起裂至峰值荷载阶段,失稳断裂阶段则为峰值荷载至完全破坏阶段。在稳定断裂过程中,根据功−能原理,外力做的功一部分用于裂缝开裂,另一部分以弹性应变能的形式储存在试件内。在失稳断裂过程中,裂缝开裂的能量源于外力功及内部应变能的释放。
整个能量消耗过程见图5所示。稳定断裂能和失稳断裂能的计算公式如下

式中:WS和WOAMO为稳定断裂功;WOIMO为达到峰值荷载时消耗的外力功,可由荷载−开口位移曲线积分得到;WU为失稳断裂功;AS,AU为试件稳定与失稳时对应的断裂面积;WAIMA为试件应变能;Phmax为峰值荷载;Kc为试件在峰值荷载处刚度[15];δ0,δc,δ1分别为起始点、峰值荷载点以及试验结束点(荷载接近与0)对应的位移。考虑到试件温度越高,下降段下降越缓慢,耗时越大,对各温度下荷载接近0 kN的定义如下:20~120 ℃时,取峰值荷载的1/40;200~450 ℃时,取峰值荷载的1/30;500~600 ℃时,取为峰值荷载的1/20。K0为试件的起始刚度,可根据起裂荷载前荷载−开口位移曲线的线性段进行求解。
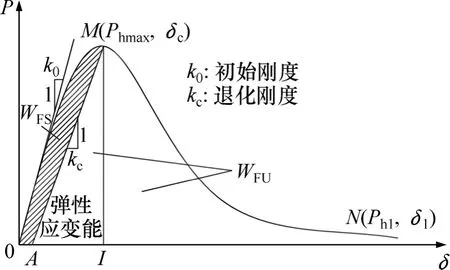
图5 混凝土试件耗能过程示意图Fig. 5 Energy consumption for an entire crack propagation period
图6所示为稳定断裂能与失稳断裂能平均值随温度的变化趋势。由图6可知:稳定断裂能GFS和失稳断裂能GFU随温度均为保持不变—增加—下降的趋势,与断裂能随温度的变化趋势保持一致。
由表2可知,稳定断裂能GFS小于整体断裂能GF,而失稳断裂能GFU大于整体断裂能GF,三者关系如下
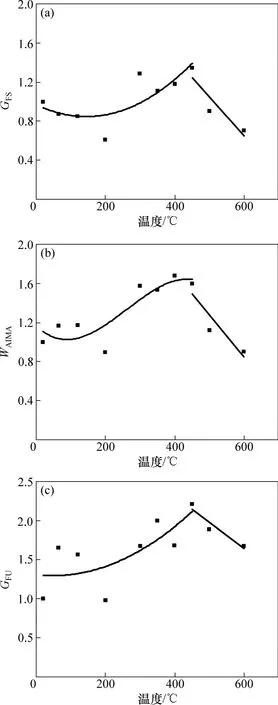
图6 稳定断裂能与失稳断裂能随温度的变化趋势Fig. 6 Relationship of GFS , WAIMA and GFU with Tm
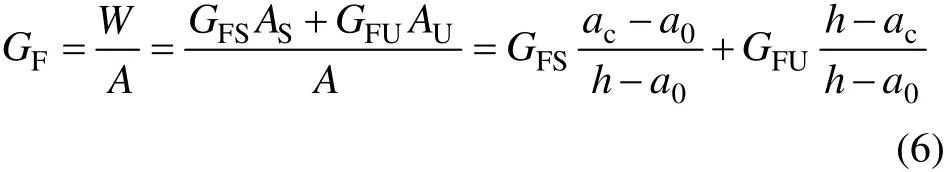
其中,GFS与GFU在GF中所占权重与试件临界裂缝发展长度成正比,即与其断裂面积AS,AU成正比。当温度在20~120 ℃时,由表2可得:AS小于AU,20 ℃时,GFS所占比例约为21%;随温度的升高,临界裂缝长度ac增加,AS大于AU,GFS所占比例明显增加,600 ℃时GFS所占比例为46%。

表2 稳定断裂能和失稳断裂能参数Table 2 Calculated values of GFS and GFU
当从能量角度考虑高温后混凝土试件的延性时,应主要考虑其稳定裂缝扩张状态下的能量吸收能力,包括裂缝表面能和试件弹性应变能的储存。当试件吸收能量的能力如图6(a)和6(b)所示时,可以评定混凝土试件的整体韧性(延性)随温度也呈现保持不变—上升—下降的趋势。
4 结论
(1) 随着温度的上升,荷载−开口位移曲线峰值荷载Pu明显下降,而与其对应的临界裂缝开口位移则显著上升,且荷载−开口位移曲线上升与下降段的斜率变缓。
(2) 对荷载−开口位移曲线进行尾部曲线拟合处理,发现对于温度不超过120 ℃的试件,采用幂函数形式更好,而对于温度超过120 ℃的试件,则采用指数函数形式进行拟合更为准确。
(3) 高温后混凝土试件断裂能GF及稳定断裂能GFS随温度的变化趋势为保持不变−上升−下降,两者在450 ℃左右发生突变。
[1] Wittmann F H. Size effect of fracture energy of concrete[J]. Engineering Fracture Mechanics, 1990, 35(1/2/3): 107−115.
[2] Petersson P E. Crack growth and development of fracture zones in plain concrete and similar materials[R]. Sweden: Division of Building Materials, Lund Institute of Technology, 1981: 6−12.
[3] Bruhwiler E, Wittmann F H. The wedge splitting test: A new method of performing stable fracture mechanics[J]. Engineering Fracture Mechanics, 1990, 35(1/2/3): 117−125.
[4] Hillerborg A. Results of three comparative test series for determining the fracture energyGFfor concrete[J]. Materials and Structures, 1985, 18(5): 407−413.
[5] Duan K, Hu X Z, Wittmann F H. Size effect on fracture resistance and fracture energy of concrete[J]. Materials and Structures, 2003, 36(2): 74−80.
[6] Duan K, Hu X Z. Explanation of size effect in concrete fracture using non-uniform energy distribution materials[J]. Materials and Structures, 2002, 35(6): 326−331.
[7] Bazant Z P, Prat P C. Effect of temperatures and humidity on the fracture energy of concrete[J]. ACI Materials Journals, 1988, 85(4): 262−271.
[8] Baker G. The effect of exposure to elevated temperatures on the fracture energy of plain concrete[J]. Materials and Structures, 1996, 29(6): 383−388.
[9] Zhang B, Bicanic N, Pearce C J, et al. Residual fracture properties of normal and high-strength concrete subject to elevated temperatures[J]. Magazine of Concrete Research, 2000, 52(2): 123−136.
[10] Nielsen C V, Bicanic N. Residual fracture energy of high-performance and normal concrete subject to high temperatures[J]. Materials and Structures, 2003, 36(8): 515−521.
[11] PENG Gaifei, YANG Wenwu, ZHAO Jie, et al. Explosive spalling and residual mechanical properties of fiber-toughened high-performance concrete subject to high temperatures[J]. Cement and Concrete Research, 2006, 36(4): 723−727.
[12] 张东, 刘娟淯, 陈兵, 等. 关于三点弯曲法确定混凝土断裂能的分析[J]. 建筑材料学报, 1999, 2(3): 206−211.
ZHANG Dong, LIU Juanyu, CHEN Bing, et al. Analysis of the determination of fracture energy of concrete using three-point-bending method[J]. Journal of Building Materials, 1999, 2(3): 206−211.
[13] 徐世烺, 赵艳华, 吴智敏, 等. 楔入劈拉法研究混凝土断裂能[J]. 水力发电学报, 2003(4): 15−22.
XU Shilang, ZHAO Yanhua, WU Zhimin, et al. The experimental study on the fracture energy of concrete using wedge splitting specimens[J]. Journal of Hydroelectric Engineering, 2003(4): 15−22.
[14] XU Shilang, ZHAO Yanhua, WU Zhimin. Study on the average fracture energy for crack propagation in concrete[J]. Journal of Materials in Civil Engineering, 2006, 18(6): 817−824.
[15] Rajendra K N. True fracture energy of concrete[J]. ACI Material Journal, 1999, 96(2): 213−225.
(编辑 赵俊)
Determination of residual fracture energy of concrete subjected to elevated temperature
SHANG Xingyan, YU Kequan, LU Zhoudao
(College of Civil Engineering, Tongji University, Shanghai 200092, China)
The wedge-splitting method was employed to determine the residual fracture energyGFof post-fire concrete specimens. All the specimens were subjected to 10 temperatures varying from 20 ℃ to 600 ℃. The effect of the long tail of load-displacement (P-CMOD) was considered by curve fitting when calculating GF. The results show that when the temperature is less than 120 ℃, the power function has a better agreement; beyond 120 ℃, and the exponential function has more accuracy. According to the wholeP-CMOD, the residualGF, the stable fracture energy GFSand the unstable fracture energyGFUare determined. The results demonstrate that all three values sustain a hold−increase−decrease tendency with the increase of temperatures, which means that the residual fracture behaviors share the same tendency with the increase of temperatures.
wedge-splitting method; post-fire; concrete; curve fitting; fracture energy
TU375.4
A
1672−7207(2014)02−0589−07
2013−06−25;
2013−09−30
国家自然科学基金资助项目(51378397);土木工程防灾国家重点实验室基金资助项目(SLDRCE09-D-02)
陆洲导(1957−),男,上海人,博士,教授,从事混凝土抗火研究;电话:13901731892;E-mail:lzd@tongji.edu.cn

