基于波浪谱的三维随机波浪数值模拟及仿真

赵 珂，李茂华，郑建丽，田冠楠

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001； 2.中国水产科学研究院 渔业机械仪器研究所，上海 200092)

0 引 言

舰船、海洋平台等海洋结构物在海洋中工作，鱼雷及潜射导弹的发射航行等都不可避免的受到波浪载荷的影响，波浪载荷的研究成为海洋结构物设计的重要组成部分，而准确确定波浪载荷的前提是建立可反映真实海浪的波浪模型。目前对于波浪研究的主要方法仍然是把波浪看作理想的规则波模型，然而自然界中的海浪是一种非常复杂的物理现象，波面上风速风向的变化，波浪内部运动破碎等因素都使海浪成为一种高度不规则和不可重复的现象[1-2]，即随机波浪。因此，只有随机波浪模型才能真实反映实际海浪，为海洋结构物的研究提供准确的波浪信息。

本文采用Matlab软件对三维随机波浪进行仿真，生成波面图像，并对图像显示进行处理使其视角上更加接近真实波浪。为舰船、水下武器(鱼雷、潜射导弹等)的设计研究提供参考。

1 波浪模型的建立

1.1 随机波浪的数学模型

实际波浪的运动过程是一个复杂的三维随机过程，二维波浪模拟不能够有效地反映实际波浪的运动情况，需要进行更加精确的三维随机波浪模拟。 将三维随机波浪看成是由许多个不同波高、不同周期、不同相位、不同运动方向的余弦波叠加而成，设波面方程为z=η(x,y,t)，则其波面模型可用式(1)表示[1]

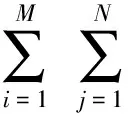
ωdit+βij]。

(1)

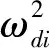
1.2 波浪参数的确定

在进行随机海浪仿真时，首先要选取适宜的海浪谱作为模拟对象(即靶谱)，本文选取ITTC规定的标准波浪谱Pierson-Moscowitz谱(PM谱)[3-4]作为靶谱，其表达式为

式中，ω为频率，H1/3为有义波高，设海面风速为v，则H1/3=0.0214v2。

由于PM谱描述的是能量随频率的变化，而对于三维随机波浪，其能量分布与频率和方向角都有关，并且认为频率和方向角的影响相互独立，则引入只与方向角α相关的方向扩展谱函数Df(α)：

最终，可得到三维随机波浪的方向波谱：

S3D(ω,α)=SPM(ω)·Df(α)。

(4)

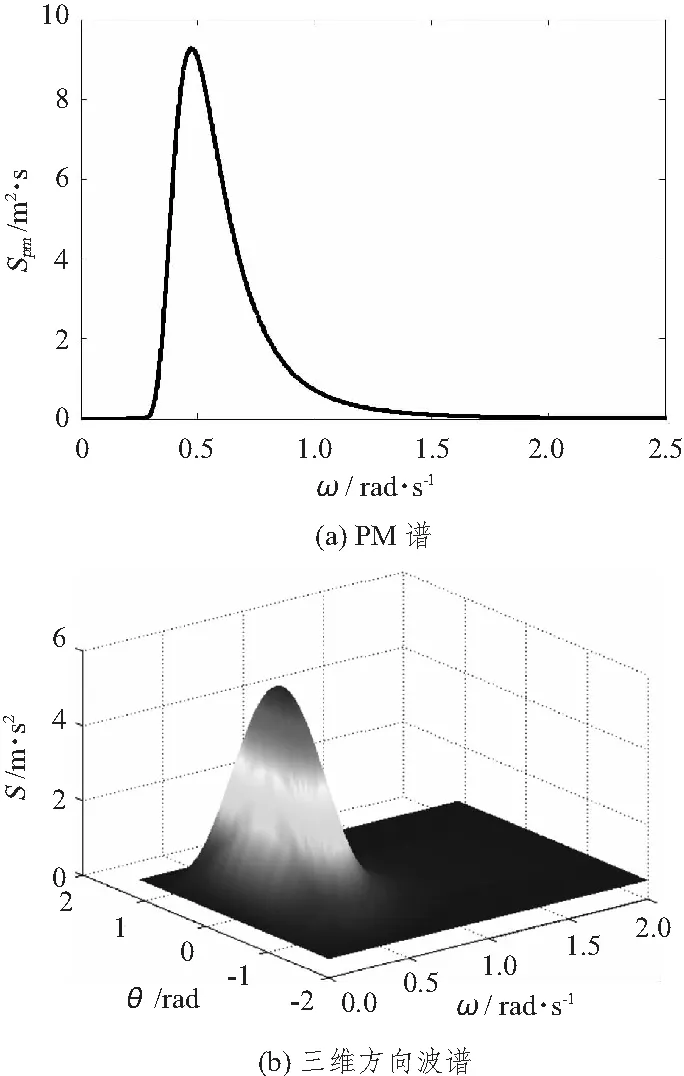
图1 波浪谱示意图Fig.1 Graph of wave spectrum

对传播方向角α进行划分和选取时，设方向角的变化范围为主波向αmain两侧-π/2～π/2的范围，将此区N等分，每一等份的宽度为dα=2π/N，选取每段的中心方向角作为代表方向角αdj。

方向角划分完毕后，进行代表频率的选取。设PM谱的能量集中在频谱区间[ωs，ωx]内， 则其余部分可忽略不计，假设在高低频侧各允许略去总能量的μ部分(本文取μ=0.003)， 频谱区间的上、下限ωs，ωx可通过下式确定：

确定频谱区间后要进行频谱区间的划分及代表频率的选取。频谱区间划分一般有等分频率法和等分能量法2种方法，为防止按等频率法划分频率区间时，模拟得到的波浪以周期2π/dω重复出现，使模拟结果与实际海浪不符，本文采用等分能量法。等分能量法是将谱频区间划分为M个能量相等的区间，各区间的分界频率ωi由式(6)确定，则每个频率区间的宽度为dω=ωi+1-ωi。频谱区间划分完毕后，选择各个频谱区间的中心频率作为代表频率，其计算式如式(7)所示。

(6)

自此，通过对频率和方向角的划分，把待模拟的波浪离散成了M×N个单元，每个单元组成波的波幅ζij可采用式(8)得到

波浪相位角βij应在0～2π范围内均匀分布，为保证生成的随机数分布均匀，从而保证仿真效果能够尽可能符合实际情况，采用线性乘同余法[5]生成所需伪随机数，式(9)～式(10)为乘同余法递推公式，xij为0～B范围内均匀分布的随机数，yij为 0～1内均匀分布的随机数，最后，根据式(11)得到i×j个 0～2π范围内均匀分布的随机数βij。

xij=λx(i-1)j(modB)， (i=1,2,3...)，

(9)

yij=xij/B。

(10)

βij=2πyij。

(11)

式中，取B为素数，λ为B的原根时，能达到最大周期T=B-1，因此B可适当取大些，使生成的随机序列的周期大。

2 波浪仿真

运用Matlab软件实现波浪仿真。首先，采用上节介绍的方法确定频率分割数M，方向角分割数N，代表频率ωdi， 代表方向角αdj， 相位角βij， 波幅ζij及波数ki， 并给定某一时刻t； 接着选定待仿真波浪的波面范围，即x和y的范围；仿真实现时，对于某一选定的位置(x,y)， 运用式(1)得到一个叠加的波高，这样通过改变(x,y)值， 就可得到三维波面的图像。此三维波面图像显示的为固定时刻t的波面效果，随着t值的连续变化，就可得到随时间变化的波面图像。

图(2)中(a)和(b)分别为模拟3级浪、5级浪的波面图像，模拟所需具体参数及文献中的参考波高[6-7]和本仿真最大波高对比结果如表1所示。

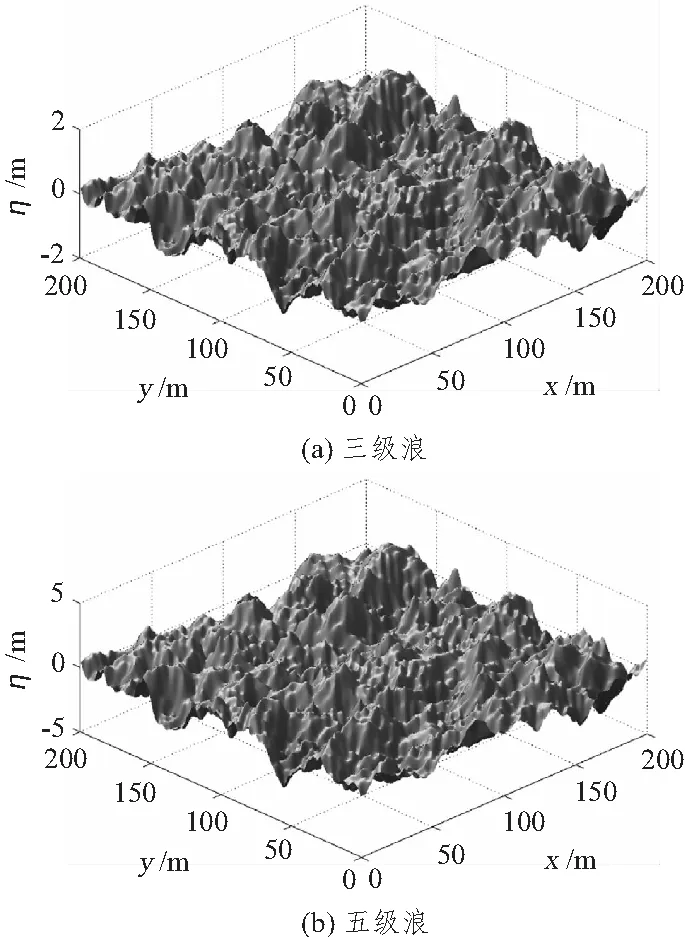
图2 三维随机波浪仿真曲面Fig.2 Simulate surface of 3-D random wave

浪级时刻t/s频率划分数M方向角划分数N风速范围/m·s-1选取风速/m·s-1波高参考范围/m仿真最大波高/m3级浪2605055～88[05125]115级浪26050115～1413[2540]34

3 结 语

本文针对三维随机海浪的仿真进行研究，首先建立基于PM谱的三维随机海浪数学模型，并通过对频率和方向角的划分进行了数值离散。在波浪相位角的选取上，为使得到的随机数列效果更好，采用乘同余法；最后运用Matlab软件生成波面，引入Matlab自带的brighten()， colorma()函数[8]并开启lighting模式对波面进行美化，使显示效果更具真实性。将仿真得到的最大波高与参考波高范围对比，结果表明，仿真结果满足要求，本方法能够快速有效地进行三维随机波浪的仿真。本研究下一步的工作是将水中航行体的受力与随机波浪结合起来，从而计算出随机波浪对于航行体运动的影响。

[1] 俞聿修.随机波浪及其工程应用[M].大连:大连理工大学出版社,2003.

YU Yu-xiu.Random wave and its applications to engineering[M].Dalian:Dalian University of Technology Press,2003.

[2] 竺艳蓉.海洋工程波浪力学[M].天津：天津大学出版社，1991.

ZHU Yan-rong.Ocean engineering wave mechanics[M].Tianjin:Tianjin University Press,1991.

[3] PIERSON W J,MOSKOWITZ L.A propose spectral form for fully developed seas based on the similarity theory of SA Kitaigorodski[J].Jour.Geophys.Res.,1964,69(24):5181-5190.

[4] BOCCOTTI P.A method to obtain the directional wave spectrum[J].Ocean Engineering,2004(31):539- 545.

[5] 符宁.均匀随机数的线性同余生成方法[D].吉林：吉林大学,2007.

FU Ning.The methods for generating the random numbers:liner congruence generator[D].Jilin:Jilin University,2007.

[6] KINSMAN B.Wind waves[M].New Jersey:Prentice Hall In.,1965.

[7] 潘玉田，马新谋， 杨栋.三维随机波浪的数值仿真研究 [J].火箭发射与控制学报，2010,9(3):5-8.

PAN Yu-tian,MA Xin-mou,YANG Dong.Study on numerical simulation of 3D random wave[J].Journal of Gun Launch & Control,2010,9(3):5-8.

[8] 李晖，郭晨，李晓方.基于Matlab的不规则海浪三维仿真[J].系统仿真学报，2008,15(7)：1057-1059.

LI Hui,GUO Chen,LI Xiao-fang.3D visual simulation of irregular ocean wave based on matlab [J].Journal of System Simulation,2008,15(7):1057-1059.