数据挖掘约简算法的应用
黑龙江 洪学银
系统应用中,S=(U,C,D,V,f)每一元素表示决策规则。在决策规则中条件的属性取值不是必要的。规则的约简算法就是要约去规则中的不必要的属性参数,计算规则的核和简化。属性约简之后,对规则的冗余参数进行剔除。粗糙集理论的应用重点在约简属性和提取规则,但粗糙集知识中上下近似元素约简出的规则不一定是最优化规则。因此,组建粗糙集知识与信息熵的关系图,得出粗糙性理论的度量性表示,把信息熵理论和粗糙集理论相结合,提出规则集,得出信息熵约简算法应用方法。
一、基本概念
2.条件熵:知识属性集合Y(U|IND(Y)={Y1,Y2,…,Ym})相对于知识(属性集合)
U/ind(X)={X1,X2,…,Xn}的条件熵:H(Y|X)为:
3.互信息:T=
二、方法描述
应用粗糙集知识约简出的规则不一定是最简规则,规则中会存在属性值是不必要的。在决策表中添加属性引起互信息的改变大小为该属性重要性的度量,SGF(a,A,D)值越大,表示在已知A的条件下,属性a对于决策D就越重要。论域上的不可分辨关系和信息熵知识可以对确定性规则进行约简。
三、实例分析
假设论域 U={1,2,3,4,5,6,7,8},属性的集合 C={Solar energy,Volcanic activity,Residual CO2},决策属性D为Temperature,原始数据表见表1-1:
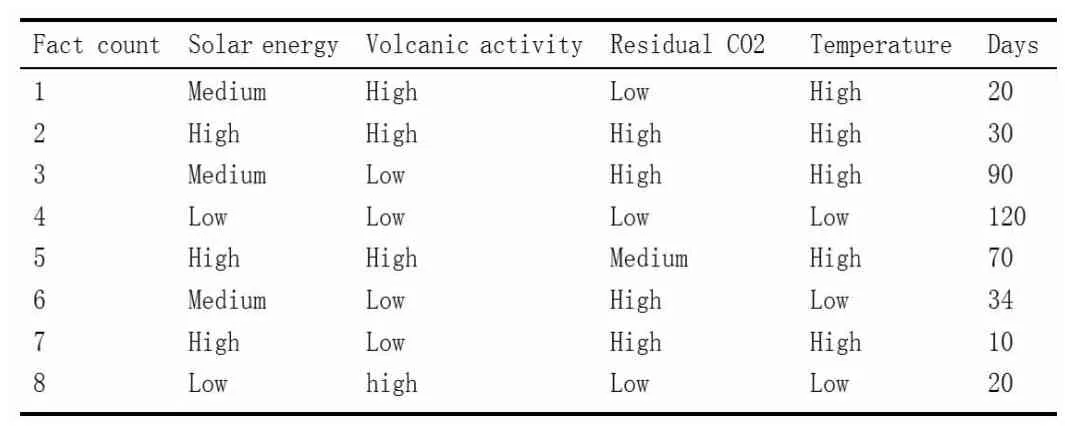
表1-1 一个天气决策表
计算C对于D约简过程,得出C0={solar,volcanic}是C对于D的约简。
提取规则:
计算决策属性同类相对于U/C0的下近似值,得出确定性的规则
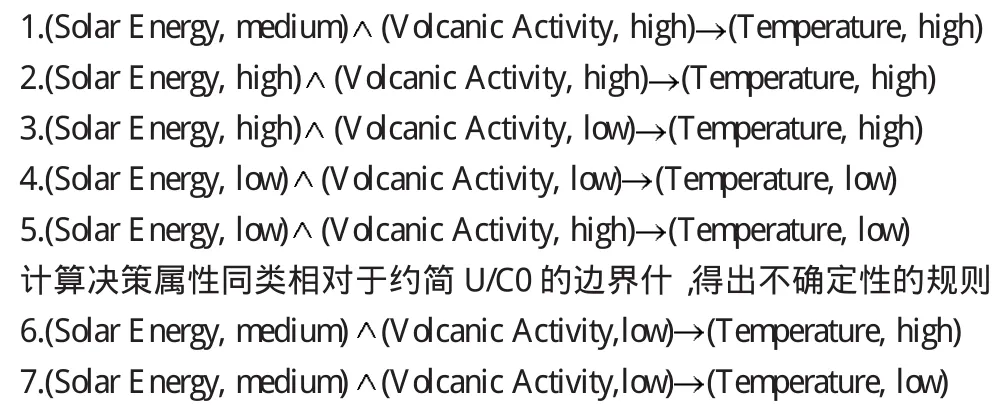
计算表1-1中决策属性的信息熵,约简的属性solar,volcanic的互信息是:
H(D)=-1*(130/270*log2(130/270)+140/270*log2(140/270))=0.999
属性Solar Energy的条件熵是:
H (D|C1)=-1*(110/270)*(110/110)*log2(110/110)-1*(20/270)*20/20*log2(20/20)-1*(140/270)*(140/140)*log2(140/140)=0
属性Volcanic Activity的条件熵是:
H(D|C2)=-1*140/270*(120/140*log2(120/140)+20/140*log2(20/140))-1*130/270*(120/130log2(120/130)+10/130*log2(10/130))=0.345
两种属性的互信息是:
Gain(Solar Energy)=0.999
Gain(Volcanic Activity)=0.654
因为属性solar互信息较大,决策重要性高,Volcanic较小,得出要先在量化规则中去掉Volcanic属性值,当去掉Volcanic,当Solar Energy为高时,规则中没有冲突的规则,所以对应的规则2、规则3中属性Solar Energy的值标是1;若Solar Energy为低,没有产生冲突性规则,所以对应的规则4、规则5中属性Solar Energy的值也是1;池Solar Energy为中,规则1,规则6与规则7产生冲突性规则,所以确定性规则1属性Solar Energy值标记3。然后按照约简方法进行计算,简化得出确定性规则集是:

四、小结
通过研究基于应用的粗糙集知识和信息论结合的约简算法,将信息论实例应用在决策信息规则约简算法中,规划出信息熵与知识的关系结构,得到基于应用的信息熵约简算法,通过实例应用,约简算法得出合理的最优化的约简规则,更有效地应用到数据统计中。
[1]童舟,罗可.基于Rough Set带结论域的关联规则挖掘[J].计算机工程与应用,2006,42.
[2]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11(5):341~356.
