擦窗机底盘四点支撑反力计算探讨

兰阳春，谢建琳

（上海普英特高层设备有限公司，上海 200127）

擦窗机底盘一般分为固定式和运行式，有4个支点，固定式底盘受到的支撑反力，即为擦窗机对建筑基础的施加力，是建筑设计结构梁的验算条件之一。而运行式底盘其轮压是擦窗机运行轮对轨道的垂直压力，即为擦窗机轨道对擦窗机底盘的支撑反力。本文主要针对四点支撑的擦窗机底盘支撑反力进行分析计算，比较后得出哪种计算方法更适合擦窗机底盘支撑反力计算。

1 擦窗机底盘的刚性及支撑的刚性

1.1 刚性底盘假设

认为底盘是绝对刚性，在载荷作用下底盘的4个支撑点也不发生变化，即始终保持在一个平面上。

1.2 铰接底盘假设

认为底盘为4根简支梁构成的平面铰接框架，四支撑点是框架的铰支座，在载荷作用下，四支撑点随基础变形而位移，不再保持同一个平面上，即支撑具有一定的弹性变形。

1.3 擦窗机底盘支撑的刚性假设

固定式度盘通过地角螺栓直接连接建筑基础，可初步视为其具有足够的刚度，即不发生位移，在受力情况下能保持在同一个平面上。而运行式底盘，由于运行式底盘自身具有摆臂，并且其受力于轨道上，因此可视为其支撑刚性有限，在受力情况下会发生位移，不再保持在同一个平面上。

2 擦窗机刚性底盘假设计算支撑反力

擦窗机底盘由A、B、C、D四点支撑（图1），其非旋转部分重力为G1，旋转部分重力为G2，旋转中心位于底盘中心，重心G1与底盘中心与x轴线夹角为φ。

图1 刚性底盘假设支撑反力示意图

刚性底盘各支撑点在静止状态下的垂直反力分别为

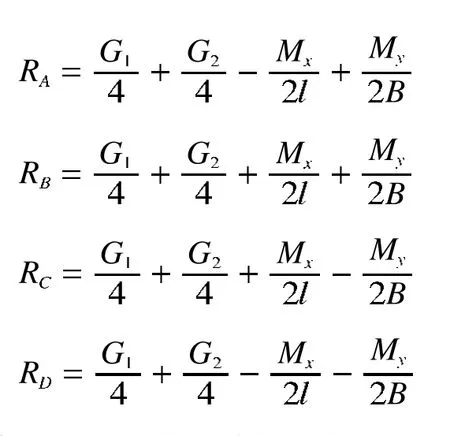
式中G1——非旋转部分自重；

G2——旋转部分自重；

Mx、My——旋转部分载荷向旋转中心转化的力矩在x、y方向的分力矩，Mx=G2cosφ，My=G2sinφ。

3 擦窗机铰接底盘假设计算支撑反力

按铰接底盘计算支承反力，设想虚梁A1B1通过重心G2，并简支在铰接框架的简支梁AD、BC上（图2）。旋转重心G2距离底盘中心距离为S，根据力与力臂平衡的反比关系即可以求出各支撑点的支撑反力。

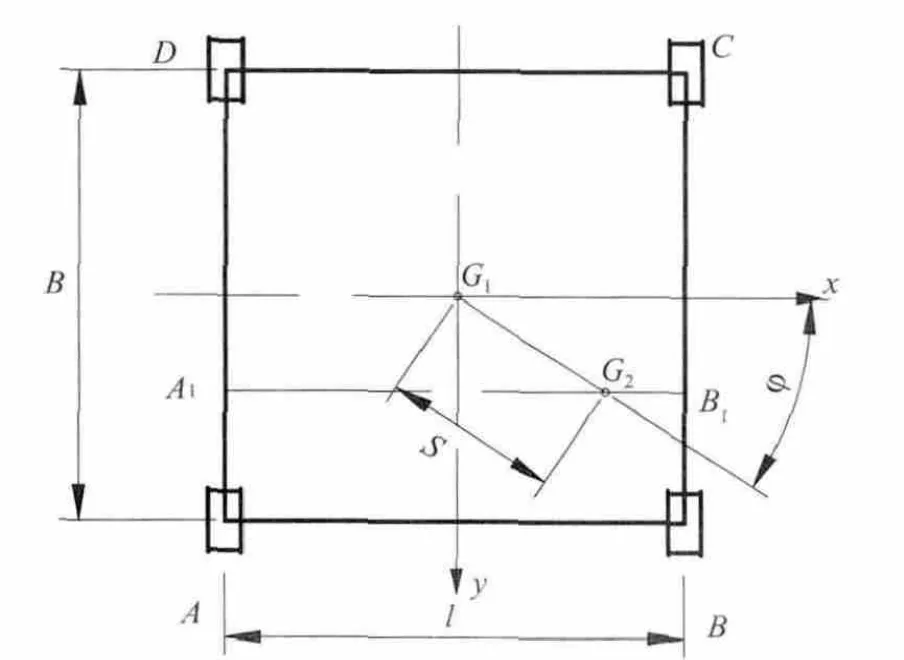
图2 铰接底盘假设支撑反力示意图

根据简支梁特点，可先求出A1、B1点的支撑力分别为

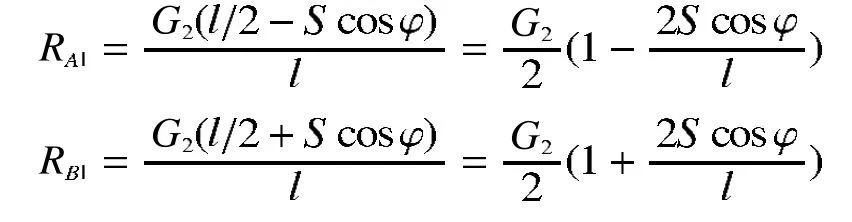
再将AD梁看作简支梁，则可求得

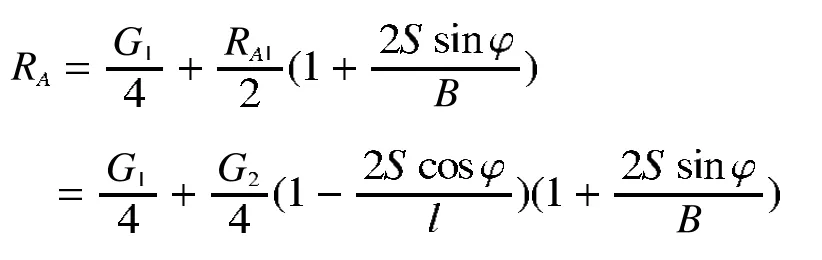
同理，可以求得其它各点支撑力

4 两种公式计算举例

4.1 设定数据

下面通过假设一组数据分别代入两种公式，求出其支撑反力值，以查看其二者之间的差别。为了便于计算，特设定：B＝l＝1500mm，S＝800mm，G1＝5000kg，G2＝5000kg，φ＝45°。

通过计算可得出刚性假设下各支撑点反力为：RA=25.00kN，RB=43.86kN，RC=25.00kN；RD=6.14kN。铰点假设下各支撑点反力为RA=17.89kN；RB=50.96kN，RC=17.89kN，RD=13.25kN。

4.2 举例结论

从上面数据看，铰点假设的最大支撑反力比刚性假设的最大支撑反力大，其最小轮压同样比刚性假设支撑反力大。

5 有限元分析

那么两种计算方法，出现两种不同的结果，到底哪种计算结果更符合实际工程中擦窗机底盘的支撑反力的实际情况呢，下面通过有限元来分析比较。建立一个空心管拼接而成的底盘模型，通过对底盘模型的约束不同分别进行分析。

5.1 刚性约束建模

约束：底盘4个支撑点完全固定，并且不能发生位移。

加载：底盘受到均布载荷非旋转重力，底盘上表面受到集中载荷旋转重力。

图3中FZ表示垂直方向力，FX、FY表由于内力影响而产生的其它两个方向的水平力。从图3中可以看出，四支撑点的各个支撑反力如下：RA＝15.90kN，RB＝54.80kN，RC＝16.00kN，RD＝13.10kN。

图3 刚性约束有限元分析

根据建模时的约束情况，这种约束更符合擦窗机工程中固定底盘的形式，即4个支撑点焊于建筑基础上。可以看出，有限元分析结果与铰接假设更接近。

5.2 铰接约束建模

约束：底盘4个支撑点水平方向自由，可发生位移，并且在垂直方向上存在一定的弹性位移。

加载：底盘受到均布载荷非旋转重力，底盘上表面受到集中载荷旋转重力。

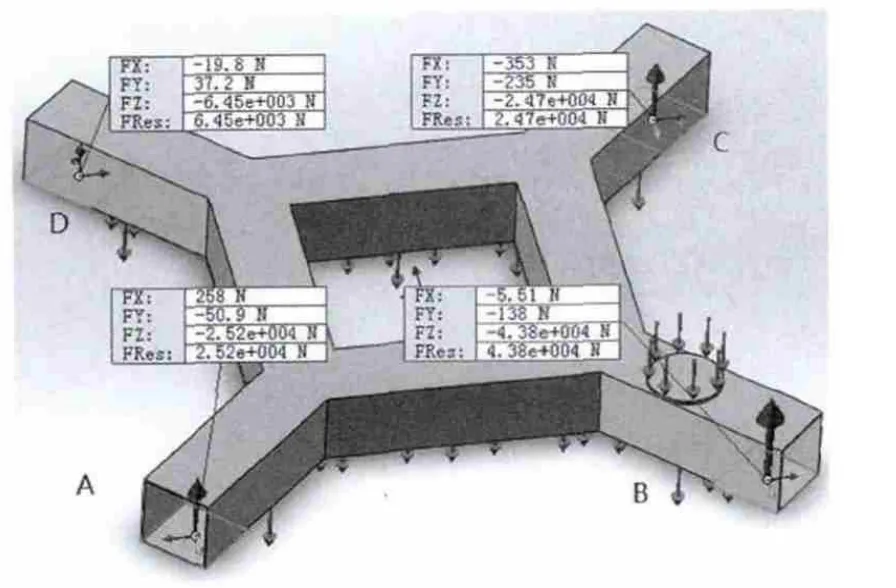
图4 铰接约束有限元分析

从图4中可以看出，4支撑点的各个支撑反力如下：RA＝25.20kN，RB＝43.80kN，RC＝24.70kN，RD＝6.45kN。

根据建模时的约束情况，这种约束更符合擦窗机工程中，带运行底盘的形式，即4个支撑点受力于擦窗机轨道上，轨道受力后存在一定的弹性变形。可以看出，有限元分析结果与刚性假设更接近。

6 结 语

综上所述，擦窗机四点支撑底盘在受力时，应根据不同的假设模型选择不同的计算公式，而作为固定式的四点支撑应根据铰接公式计算，此时计算的数据最大支撑反力比刚性假设公式的要大，而带有行走的四点支撑底盘，更适合用刚性假设条件计算公式。建议实际工程根据两种计算结果合理地取其最大值，作为擦窗机设计、建筑设计的参考。

[1]张质文.起重机设计手册[M].北京：中国铁道出版社，1998.

[2]成大先.机械设计手册[M].北京：化学工业出版社，2011.