菱锌矿的硫化电位控制浮选机理研究

陈经华，张方齐，吴熙群

（1.北京矿冶研究总院矿物加工科学与技术国家重点实验室，北京102600；2.庄胜矿产资源集团有限公司，北京100052；3.万宝矿产有限公司，北京 100053）

菱锌矿的硫化电位控制浮选机理研究

陈经华1，张方齐2，吴熙群3

（1.北京矿冶研究总院矿物加工科学与技术国家重点实验室，北京102600；2.庄胜矿产资源集团有限公司，北京100052；3.万宝矿产有限公司，北京 100053）

以十二胺为捕收剂、硫化钠为活化剂，通过菱锌矿单矿物浮选试验系统研究了硫化钠用量、硫化时间、搅拌条件、加药方式以及矿浆p H值对其浮游性和硫化电位的影响。利用相关系数法分析了各因素对硫化电位的影响趋势及相关性。采用多元回归方法建立了浮选回收率与硫化电位的数学模型。利用Matlab软件拟合出硫化电位与主要因子之间的数学模型方程，结合回收率与电位的数学模型，因素与电位的数学模型为实现硫化过程的优化调控提供了理论基础。

菱锌矿；硫化过程；多元回归分析；数学模型；硫化电位控制浮选机理

锌是非常重要的有色金属之一，其消费量仅次于铜和铝。锌产品的用途广泛，需求量逐年加大，这就对锌资源的利用提出了较高的要求［1］。我国氧化锌矿产资源丰富，如能提高其利用率，可以缓解现阶段硫化锌矿资源日趋减少、锌再生产业发展缓慢造成的锌产品量不足的问题［2－4］。菱锌矿是最有工业价值的氧化锌矿物之一［5］，一直以来对于菱锌矿开发利用的相关研究很多［6－11］。目前，较为成熟的回收菱锌矿的方法是硫化钠活化－胺浮选法。本研究以十二胺为捕收剂，硫化钠为硫化活化剂，对菱锌矿硫化钠活化过程中的电化学行为进行了研究，分析了菱锌矿硫化活化过程中的电位特性，为菱锌矿的硫化过程电位调控浮选提供了理论基础，也为氧化锌资源利用工艺的发展提供了新的研究思路。

1 试验用材及方法

1.1 试验矿样、试剂及设备

本试验使用的菱锌矿采自云南省会泽铅锌矿，将高纯度菱锌矿矿块经锤碎、手选、实验室小型颚式破碎机与对辊式破碎机破碎、瓷球磨磨细，筛分得到－0.074＋0.038mm粒级产物。使用去离子水对矿样进行多次清洗，自然晾干，保存在磨口瓶中。经化学分析菱锌矿纯度在94%以上，符合单矿物浮选试验要求。

试验中使用的水都是去离子水。所用药剂中，十二胺、硫化钠均为分析纯试剂，化学纯的氢氧化钠与盐酸控制p H值，松油醇为起泡剂。

试验中IviumStat电化学工作站在线获取硫化活化电位。工作电极有测量硫离子电极电位的p Ag/S－1型硫离子选择性电极，测量矿浆电位的213－01型铂电极，参比电极为232型饱和甘汞电极。采用PHSJ－3F型p H计测量矿浆p H值，测量电极为E－201－9型p H复合电极。

1.2 试验方法

单矿物浮选试验使用XFGC－Ⅱ型挂槽式浮选机，每次试验称取3g菱锌矿，加入改装过的浮选槽中，同时加入50m L去离子水。试验流程：将电极与工作站连接，开启IviumSoft软件并调整测量参数，打开连接工作站与电脑的IviumStat仪器，开始在线测量并记录矿浆电位及硫离子电极电位；调整叶轮转速，调浆，加入硫化钠搅拌一定时间，测量矿浆p H值，加入捕收剂搅拌2min，加入起泡剂搅拌1min；关闭IviumStat仪器，拿出电极用注射器将粘附在电极上的矿物清洗入槽中，刮泡3min；泡沫产品烘干、称重，计算回收率。

2 硫化电位控制浮选数学模型

采用多元回归方法［12－13］拟合出一个数学模型方程来表征浮选回收率与硫化电位之间的关系。利用相关系数法［14］分析各影响因素对硫化电位的影响趋势及相关性，找出主要影响因子。利用Matlab软件［15］拟合出硫化电位与主要因素之间的数学模型方程，实现通过主要因素对硫化电位的调节，进而实时控制浮选回收率的目的。

2.1 菱锌矿回收率与硫化电位的数学模型

选取硫化钠用量、硫化时间、搅拌条件、加药方式以及矿浆p H值五个因素的条件试验的相关数据进行数学公式拟合。采用准牛顿法（BFGS）＋通用全局优化法进行数学模型方程的拟合，结果见图1、图2。

图1 菱锌矿回收率与矿浆电位数学模型方程拟合曲线

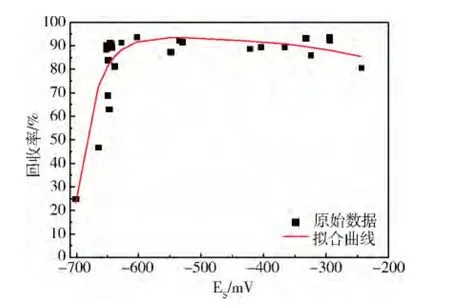
图2 菱锌矿回收率与硫离子电极电位数学模型方程拟合曲线

拟合方程为：y＝ Exp（（4.5321＋0.0256x＋4.4606x2）/（1＋0.0058x＋1.1002x2）），其中y为回收率，x为矿浆电位EPt值。拟合方程的均方根误差（RMSE）为 4.0231，误 差 平 方 和 （SSE）为420.8188，相关系数R为0.9664，决定系数（DC）为0.9339，接近于1。表明拟合的数学模型方程很好的反映了矿浆电位EPt值与菱锌矿回收率之间的关系，并且在一定的矿浆电位EPt值范围内，菱锌矿的浮游性较好。

拟合方程为：y＝3756.7531/x－1.4501Exp（－0.0319x）＋100.9559，其中y代表回收率，x代表硫离子电极电位ES值。拟合方程的均方根误差（RMSE）为 8.3618，误 差 平 方 和 （SSE）为1887.8339，相关系数 R为0.8416，决定系数（DC）为0.7082。可见拟合方程基本上能够反映硫离子电极电位ES值与菱锌矿回收率之间的关系，但是拟合的效果相比矿浆电位EPt值与菱锌矿回收率的较差。

由图1、图2可以看出，在一定的硫化电位范围内，菱锌矿的浮游性较好，在菱锌矿的浮选过程中，通过控制硫化电位可以实现菱锌矿较高的回收率。

2.2 单因素对菱锌矿硫化电位的影响分析

2.2.1 单因素对硫化电位的相关性分析

计算单因素与菱锌矿硫化电位之间的相关系数。计算公式如式（1）所示，计算结果如表1所示。

式中：r为相关系数；x为自变量；y为因变量。

表1 硫化电位与单因素之间相关系数表

由表1可见，硫化钠用量与矿浆电位EPt值的线性相关性较为显著，相关性系数为－0.8607大于r0.01（8）。其他因素与矿浆电位 EPt值、硫离子电极电位ES值之间相关性系数均小于r0.01（n），表明两者之间不存在显著的线性关系。

试验过程中捕收剂是在硫化电位测定以后添加，因此捕收剂用量不对硫化电位产生影响。加药方式试验中电位的获取环境不同，数据点不具有连续性，并且其它因素的电位数据主要是在先加硫化钠后加捕收剂的条件下获取的，为确保建立的数学模型方程的合理性，后续的拟合也没有采用加药方式的数据。

2.2.2 单因素对硫化电位影响程度分析

单因素实现的硫化电位变化范围见表2。

由表2可以看出，硫化钠用量对矿浆电位EPt值及硫离子电极电位ES值的影响较大，可以实现最大电位变化量程的调节。硫化时间可以实现一定范围内的电位值的调节，主要是辅助硫化钠用量进行电位控制。矿浆p H值、叶轮转速对矿浆电位EPt值及硫离子电极电位ES值不产生影响。综上所述，可以用硫化钠控制电位。

表2 单因素实现的硫化电位的变化量程

2.3 主因素与菱锌矿硫化电位的数学模型

由上文第2.1节可知，硫离子电极电位ES值与菱锌矿回收率的拟合效果明显较差，因此，本文主要建立了主因素与菱锌矿矿浆电位EPt值的数学模型方程。矿浆电位EPt值与菱锌矿回收率的拟合方程能够较为准确的反映两者之间的相关关系，在一定的矿浆电位范围内，菱锌矿的浮游性较好。建立主因素与菱锌矿矿浆电位EPt值的拟合方程，通过方程实现主因素对矿浆电位EPt值的准确调节，再结合矿浆电位与回收率的关系，进一步达到因素对菱锌矿回收率的实时合理调节。

2.3.1 单因素对矿浆电位EPt值的数学模型

根据菱锌矿硫化钠用量试验数据可以拟合出硫化钠用量对矿浆电位EPt值的影响曲线，见图3。

图3 硫化钠用量对矿浆电位EPt值的拟合曲线

拟合方程1为 y＝229.4022－2.5820x＋0.0046x2－2.7697×10－6x3，其中，y为矿浆电位EPt值，x为硫化钠用量。由拟合结果知R＝0.9973，可决系数为0.9947接近于1，说明拟合方程能够准确地反映硫化钠用量与矿浆电位EPt值的关系。对上述方程求导，导数方程：y＝－2.5820＋0.0092x－8.3091×10－6x2，可知拟合方程导数恒小于零，则拟合方程是单调递减的。上述结果表明，随着硫化钠用量的增加，矿浆电位EPt值单调递减。

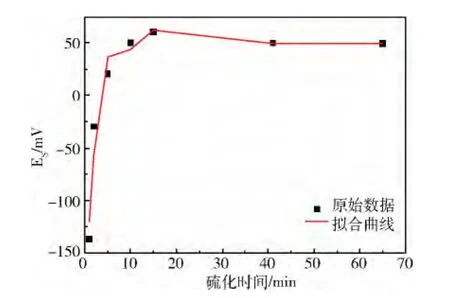
图4 硫化时间对矿浆矿浆电位EPt值的拟合曲线

根据菱锌矿硫化时间试验数据，可以拟合出硫化时间对矿浆电位EPt值的拟合曲线，见图4。拟合方程2：y＝－207.1894＋99.4117x－13.6149x2＋0.7819x3－0.0177x4＋0.0001x5，其中，y为矿浆电位EPt值，x为硫化时间。由拟合结果知R＝0.9785，可决系数为0.9574接近于1，可见拟合方程能够很好的说明硫化时间与矿浆电位EPt值之间的关系。

2.3.2 主因素对矿浆电位EPt值的数学模型

表3 回归方程的系数置信区间与统计量

由表3可见，决定系数r2＝0.9820，接近于1，复相关系数r＝0.9909大于r0.01（13）＝ 0.6411，F＝659.3597大于F0.01（2，12）＝6.93，说明多元线性回归整个效果特别显著，由此说明用该回归方法建立的数学模型方程是合适的，基本反映了观测值与回归值之间的关系，拟合程度较好。硫化钠用量、硫化时间对矿浆电位EPt值的影响规律可以用这一数学模型方程来描述。模型回归值与观测值对比见图5。

图5 矿浆电位拟合曲线与原始数据对比图

3 结论

在浮选过程中，硫化电位是可以通过测试仪器进行实时监测的，而影响因素的调整对矿物浮选的影响可以很快地体现在电位的变动上，并且回收率与电位相关，因此可实现影响因素对浮选回收及时、准确地调整。本文利用多元回归方法和相关性分析等系统研究了硫化电位控制的规律性，并拟合出了菱锌矿回收率与硫化电位，因素与硫化电位之间的数学模型方程，揭示了硫化电位控制浮选的机理。

1）单因素对菱锌矿浮选矿浆电位EPt值以及硫离子电极电位ES值的相关性和影响程度分析结果表明，单因素与硫化电位之间并没有极为显著的线性相关关系，硫化钠用量以及硫化时间对矿浆电位的影响较大，可以实现较大量程范围内的调节，是硫化电位的主要影响因素。

2）拟合结果表明，菱锌矿回收率与矿浆电位EPt值之间的数学模型方程能够很好的反映两者之间的关系，并且由拟合曲线图可以看出，在一定的硫化电位范围内，菱锌矿的浮游性较好；主要影响因素与矿浆电位EPt值之间的数学模型方程能够很好的反映两者之间的相关关系，通过方程可以实现因素对矿浆电位EPt值准确快速的调节。

3）菱锌矿硫化电位控制浮选机理的关键点是利用回收率与电位之间的关系、因素与电位之间的关系实现硫化活化过程的及时、理性的优化调控。

［1］雷力，周兴龙，文书明，等.我国铅锌矿资源特点及开发利用现状［J］.矿业快报，2007（9）：1－4.

［2］国土资源部矿产资源储量司.全国矿产资源储量通报［R］.国土资源部信息中心，2009.

［3］中华人民共和国国土资源部.中国矿产资源报告［M］.北京：地质出版社，2012：14－15.

［4］张庆.我国锌资源保障能力分析［J］.中国金属通报，2012，（29）：20－21.

［5］谭欣，李长根.国内外氧化铅锌矿研究进展［J］.国外金属矿选矿，2000 （3）：7－14.

［6］冯其明，张国范.氧化锌矿原浆浮选新技术［J］.中国基础科学·研究进展，2011（1）：25－27.

［7］段秀梅，罗琳.氧化锌矿浮选研究现状评述［J］.矿冶，2000（4）：47－51.

［8］吴卫国，孙传尧，朱永揩.五种有机螯合剂活化菱锌矿作用机理研究［J］.矿冶，2007，16（1）：16－21.

［9］宋振国，孙传尧，刘书杰.干/湿磨对菱锌矿浮选的影响［J］.有色金属，2009，61（1）：104－106.

［10］张祥峰.异极矿浮选理论及工艺研究［D］.长沙：中南大学，2012.

［11］韩聪，魏德洲，刘文刚，等.十二胺体系中菱锌矿的浮选行为［J］.金属矿山，2011（11）：99－110.

［12］Douglas M B，Donald G W.非线性回归分析及其应用［M］.北京：中国统计出版社，1996.

［13］祁红光.基于多元回归数学模型的分析应用研究［J］.湘南学院学报，2007，28（2）：10－15.

［14］周乃磊，王中琪，徐旭东.建立数学模型分析UV－Fenton对金属切削液废水的降解［J］.环境工程学报，2012，6（7）：2271－2275.

［15］董大校.基于 MATLAB的多元非线性回归模型［J］.云南师范大学学报，2009，29（2）：45－48.

Study on mechanism of sulfide potential－controlled flotation of smithsonite

CHEN Jing－hua1，ZHANG Fang－qi2，WU Xi－qun3
（1.State Key Laboratory of Mineral Processing Science and Technology，Beijing General Research Institute of Mining and Metallurgy，Beijing 102600，China；2.Junefield Mineral Resources Holdings Limited，Beijing 100052，China；3.Wanbao Mining Co.，Ltd.，Beijing 100053，China）

The monomineral flotation test which for investigate the influence of the dosage of sodium sulfide and collector，sodium sulfide treating time，the p H of pulp，impeller speed of flotation and the methods of adding sodium sulfide and collector on the floatability of mineral，pulp potential and sulfide ion electrode potential have been conducted using dodecylamine as collector，sodium sulfide as sulfide reagent.Based on multivariable regression method，the mathematical model which reflects the relationship between flotation recovery and sulfide potential quite well was established.The influence trend of each factor on the sulfide potential and correlation between them were studied upon the correlation coefficient.Mathematical model equation between the sulfide potential and main factors was fitted out by using Matlab.The combination of mathematical models between recovery and potential，factors and potential can provides the theoretical basis for realizing the optimizing regulation of the process of sulfidation.

smithsonite；process of sulfidation；multivariable regression analysis；mathematical model；mechanism of sulfide potential－controlled flotation

张方齐，男，工学硕士，助理工程师，主要从事铜、铁、金等多金属矿选矿工作。E－mail：zhangfangqi2007＠126.com。

TD952

A

1004－4051（2014）S2－0263－04

2014－08－30

国家自然科学基金项目资助（编号：51004015）

陈经华，男，工学博士，高级工程师，主要从事有色金属矿选矿工艺及工业应用研究。E－mail：chen＿jh＠bgrimm.com。