测量平差中必要观测数的研究
胡圣武,关胜况
(1.河南理工大学 测绘学院,河南 焦作 454000)
测量平差中必要观测数的研究
胡圣武1,关胜况1
(1.河南理工大学 测绘学院,河南 焦作 454000)

测量平差中必要观测数决定了平差结果的正确性和条件方程的个数。通过长期的教学发现,正确决定必要观测数仍是一个比较困难的问题,特别是随着GPS网平差和坐标值平差的到来,必要观测数的确定越来越困难。就必要观测数在平差中的作用进行了系统总结和分析,就水准网、平面控制网、坐标值平差和GPS网的必要观测数的确定进行了系统分析和研究。
必要观测数;水准网;平面控制网;GPS网;坐标值
1 必要观测数在平差中的作用
在测量平差中,无论采用何种平差模型都要先确定必要观测数,如果必要观测数不准确,平差就不可能有正确的结果。
1)必要观测数决定平差模型的自由度。设必要观测数为 t,观测数为n ,则不管采用何种平差,其自由度r 为:r=n-t 。可知,只要观测数不变,则r 不变。
2)必要观测数确定条件方程的个数。如果不选参数,则列立的方程个数为: c=r=n-t;如果选 u个参数,且参数独立,则列立方程个数为:c=r+u=n-t+u ;如果所选u 个参数中,有 s个不独立参数,则列立方程个数为:c=r+u-s=n-t+u-s 。由此可知,必要观测数决定条件方程个数:若必要观测数太少,则条件方程数太多,所列立的方程之间不独立;若必要观测数太多,条件方程数太少,则列立方程数不足,影响平差结果。
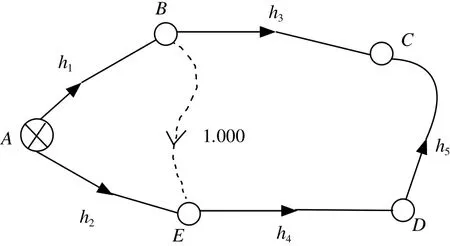
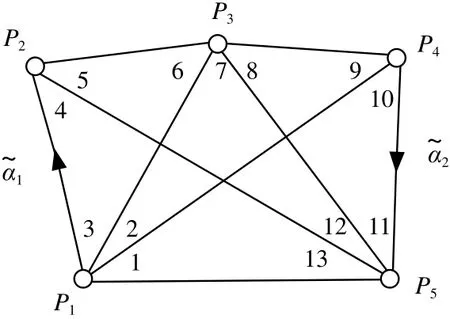
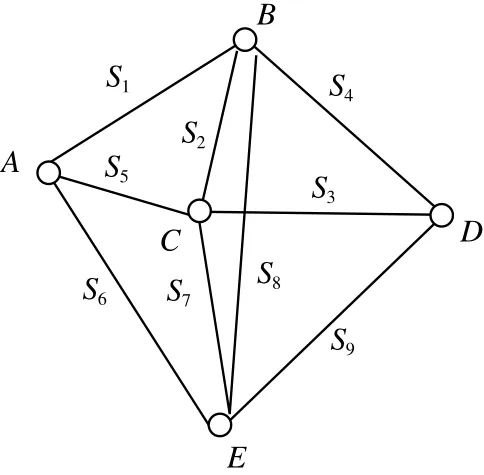
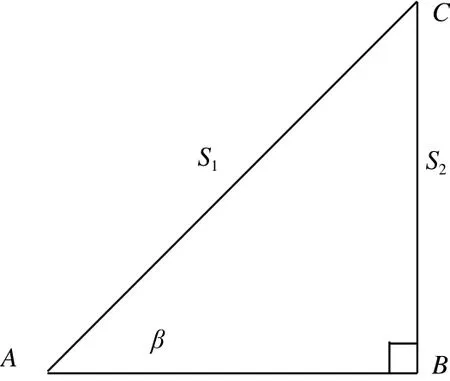
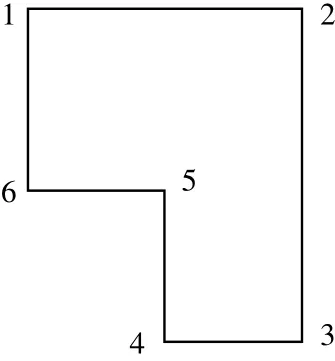
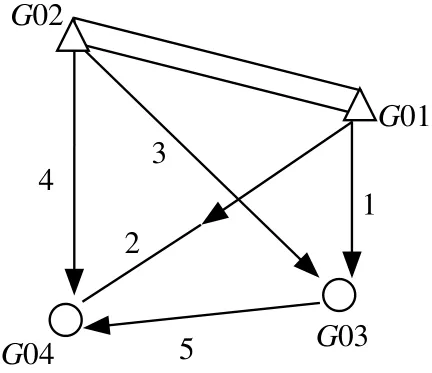
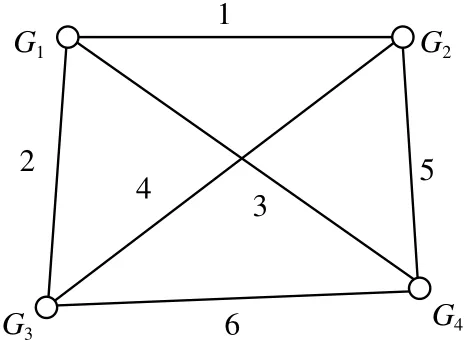
3)必要观测数确定采用平差模型的种类。平差模型的确定实际上是由所选参数个数和必要观测数确定的。设所选参数为u 个,且参数独立,有3种情况:u=0 ,则选用条件平差; u 设所选参数为 u个,且不独立参数为s 个,则有2种情况:u-s 对于水准网必要观测数的确定比较简单,主要分为3种情况:①如果有已知水准点,则必要观测数就等于未知点的个数。②如果没有已知水准点,则必要观测数就等于点数减1。③对于水准网而言,有“两点之间的高差是已知的”等特殊情况,在这种情况下,必要观测个数要减去已知值的个数。 如图1所示, A为已知点,B、C、D、E 为未知点,已知B、E 两点之间高差ΔhBE=1.000 m ,求必要观测数t 。 由于 n=5,有已知点,如果没有已知B、E 两点之间高差,则t=4 ,必要观测数t=4-1=3 。 图1 水准网示意图 1)有2个已知点的测角网。对于这种情况,各种误差处理与测量平差教材都说得很清楚,必要观测数t=2p,p 为未知点的个数。 2)有一个已知点或没有已知点的测角网。对于测角网而言,如果要进行平差则必须要有2个已知点,若不够,则需要把未知点假设成已知点。因此,对于一个已知点的情况, t=2(p-1),没有已知点,则t=2(p-2)。 3)特殊情况。测角网会出现这些情况:已知2点之间的距离、已知2点之间的方位角或两线垂直等。判断其必要观测数的步骤如下:统计出已知值的个数,设为m ;判断出该平面网的已知点,然后根据已知点的情况,判断出必要观测数t1;该平面控制网的必要观测数 t 为 :t=t1-m 。 如图2所示,观测了12个角,已知 p1、p2两点之间的方位角为 α~1,p4、p5两点之间方位角为 α~2,求其必要观测数。已知值的个数m=2 ;由于没有已知点,则 t1=(5-2)×2=6 ;必要观测数 t 为 :t=t1-2=4 。 图2 测角网示意图 边角网和测边网与测角网不同的是边都要进行测量。对于有2个已知点的测边网和边角网的必要观测数与测角网一样。没有已知点或只有一个已知点的情况与测角网不一样。 1)有2个已知点的边角网与测边网。这种情况下其必要观测数等于2倍未知点个数。 2)没有已知点或只有一个已知点的边角网和测边网。该情况与测角网一样,也要假设一个已知点或2个已知点,只不过是假设点所测的边要作为必要观测值,则已知一个点的必要观测数为t =2(p-1)+1 ,没有已知点的必要观测数为t=2(p-2)+1,其中p 为未知点的个数。 3)特殊情况。测边网或边角网有时会出现一些已知值,如两条线之间成直角、已知某条边的方位角等,判断其必要观测数的步骤如下:统计出已知值的个数,设为m ;根据其已知点的个数,确定其必要观测数 ;必要观测数为:t=t2-m 。 如图3所示,由于没有已知条件,也没有已知点,则必要观测数t=2(5-2)+1=6+1=7。直角三角形ABC ,测了2条边和1个角,是一个简单的三角网,有一个已知条件,即∠ABC=90°,没有已知点,则t2=2(3-2)+1=3。由于有一个已知值,所以该三角形测角网的必要观测数为:t=t2-1=3-1=2 (见图4)。 图3 测边网示意图 图4 直角三角形ABC示意图 一般而言,对于坐标值平差,有u 个点,每个点有一对坐标(x,y) ,则其观测数就是n=2u ,必要观测数根据确定平面一个点需要2个条件,则t=2u ,因此 n=t无法进行平差,所以没有已知值的坐标值是无法进行平差的。 一般而言,在坐标值平差中有两直线所成的角度、两线平行、图形的已知面积、两点之间的已知距离等已知值。确定其必要观测数的步骤如下:统计出已知值的个数,设为 m;计算点数设为u ,则计算出t3=2u;必要观测数为:t=t3-m 。 图5是对一直角房屋进行数字化,有6个点,12个坐标值,求其必要观测数。 解:1)由于是直角房屋,在图5中有5个直角和1个270° ,应该说是有6个已知值,但由于是多边形,确定了5个角的值,第6角的值就确定了,所以,在本图中只能算5个已知值,m=5; 2)由于有6个点,所以t3=2×6=12 ; 3)必要观测数为:t=t3-m=12-5=7 。 图5 直角房屋示意图 图6 矩形房屋线划图 图6中数字化了3个点P1、P2、P3,已知P1P3和P1P2的长度,且P1P3与P1P2保持垂直,求其必要观测数。由于有3个已知值,则m=3 ;由于有3个点,则t3=2×3=6;必要观测数为:t=t3-m=6-3=3。 GPS网可分为有已知点和没有已知点2种情况。 有已知点情况下,其必要观测数为未知点数的3倍。 如图7所示,G01、G02 为已知点,有5条基线向量,G03、G04 两个待求点,求其必要观测数。由于有2个待求点,则必要观测数:t=3×2=6。 如果没有已知点,则假设一个已知点,设待求点的个数为u ,则其必要观测数为:t=3×(u-1) 。 如图8所示,4个待求点,没有已知点,观测了6条基线向量 ,求其必要观测数。由于没有已知点,则其必要观测数为:t=3×(u-1)=3×3=9。 图7 有已知点GPS网示意图 图8 无已知点GPS网示意图 本文就必要观测数的确定进行了系统研究,特别是对坐标值平差、GPS网平差的必要观测数的确定进行了研究。需要注意以下问题: 1)虽然都是平面控制网,但坐标值平差的必要观测数的确定与测角网、测边网和边角网的必要观测数的确定不一样。 2)对于边角网和测边网,如果没有已知点或只有一个已知点,一定要掌握其必要观测数与测角网不一样,要在测角网的基础上加1。 3)GPS网是三维坐标,确定一个点需要3个条件。 4)确定已知值的个数不能重复,特别是在坐标值平差中。 [1] 姚宜斌,邱卫宁.测量平差问题中必要观测数的确定[J].测绘通报,2007(3):14-16 [2] 宁伟,欧吉坤,宁亚飞.测量平差中必要观测数确定的新方法[J].测绘通报,2010(7):45-47 [3] 宁伟,欧吉坤,张发顺.测量平差中必要观测数确定的再探讨[J].测绘通报,2010(10):11-14 [4] 左廷英,邓才华,刘庆元.关于《测量平差》课程改革的思考[J].矿山测量,2006(1):84-86 [5] 陈本富.关于《测量平差基础》教学的若干思考[J].北京测绘,2007(1):60-63 [6] 赵超英,张勤.再论经典测量平差模型间的内在联系[J].测绘通报,2006(3):26-27 [7] 邓永和.《再论经典测量平差模型间的内在联系》的研究[J].铁道勘察,2009(2):8-11 [8] 陶本藻,邱卫宁.误差理论与测量平差[M].武汉:武汉大学出版社,2012 [9] 胡圣武,肖本林.误差理论与测量平差基础[M].北京:北京大学出版社,2012 [10] 王穗辉.误差理论与测量平差基础[M].上海:同济大学出版社,2010 Research on Essential Observation Number of Surveying Adjustment byHU Shengwu Observation Number can decide correctness of adjustment outcome and number of condition equation. It is a commonplace talk of an old scholar of the problem how to define essential observation number, but correctly defi ning essential observation number is a diffi cult question from long-term teaching. Especial advent of GPS network adjustment and coordinate value adjustment,it is more and more diffi cult to defi ne essential observation number. The paper systematic and wholly researched the question, and laid the foundation promoting its application. essential observation number,leveling network,horizontal control network,GPS network,coordinate value P207 B 1672-4623(2014)02-0121-03 10.11709/j.issn.1672-4623.2014.02.043 2013-04-28。 项目来源:山东省基础地理信息与数字化重点实验室开放研究基金资助项目(SD080707)。 胡圣武,博士,副教授,主要从事GIS基础理论和图像处理技术研究。2 水准网必要观测数的确定
3 平面控制网必要观测数的确定
3.1 测角网
3.2 边角网和测边网
4 坐标值平差必要观测数的确定
4.1 必要观测数的确定
4.2 实例分析

5 GPS网必要观测数的确定
5.1 有已知点
5.2 无已知点
6 结 语

