柯诺洛夫规则与相图*
陈飞武
(北京科技大学化学与生物工程学院 北京 100083)
柯诺洛夫规则与相图*
陈飞武**
(北京科技大学化学与生物工程学院 北京 100083)
以柯诺洛夫规则为例,引导学生去探索该规则背后蕴藏的物理图像,即气液相图。从理想溶液和稀溶液气液相图开始,进一步探讨和分析了非理想溶液气液相图中总蒸气压与气液相中A组分物质的量分数之间的定量关系。
柯诺洛夫规则 气液相图 溶液热力学
1 问题的提出
在物理化学教学中,我们发现,如果教学仍像高中一样围绕考试来开展,对大学生毕业后进入社会的各个领域往往是不利的。于是在课堂教学中提出了对大学生能力培养的问题。大学生的能力包括很多方面,对那些将来要进入科研领域的大学生来说,培养提出问题的能力、分析问题的能力、以及解决问题的能力显得尤为重要[1]。这里谈谈对分析问题能力的培养。对于这一能力的培养,问题的选择尤为重要。如果问题选择不当,分析问题能力的培养很容易回到考试这条老路上来,从而就变成了对解题能力的培养。另一方面,如果题目选得太深,为了讲清楚这个题目,就需要做很多铺垫,但这样在时间上又不允许。我们主张问题最好还是来自教材,或与教材密切相关的科研课题。这样,问题的引入就很自然,不需要过多的铺垫。关键在于对这些看似平常或司空见惯的问题,如何引导学生逐步深入下去。下面以物理化学中的柯诺洛夫规则为例,通过分析柯诺洛夫规则,引导大学生看到隐藏在规则背后的物理图像,并进一步去探讨非理想溶液中的气液相图问题。
对多组分溶液体系,根据偏摩尔量的加和公式[2-5],吉布斯自由能可以表示成如下形式:

式中nB和μB分别表示组分B的物质的量和化学势。对式(1)计算全微分,得:

在等温下,吉布斯自由能有如下的微分式[2-5]:

式中aq原意为水溶液,在这里用以泛指一切溶液,Vaq表示溶液的体积。比较式(2)和式(3),得:

假定和溶液平衡的气相为理想气体,则溶液中组分B的化学势可以表示为[2-5]:

式中pӨ表示标准压力,pB表示组分B在气相中的分压。等温下,化学势μB的微分式有如下形式:

将式(6)代入式(4),得:

考虑由A和B组成的两组分体系,气相的总压为p。设A组分在溶液和气相中的物质的量分数分别为x和y,则pA=py,pB=p(1-y)。将pA和pB的表达式代入式(7),并同时除以溶液中A和B的总物质的量(nA+nB),整理后得:

式中Vm,aq为溶液的摩尔体积。利用理想气体的摩尔体积Vm,g=RT/p,进一步整理式(8)后,得:
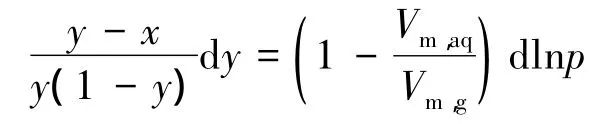
由于Vm,aq远小于Vm,g,上式可以近似写成如下形式[2]:

从式(9)得出柯诺洛夫的第一规则和第二规则[2]如下:
柯诺洛夫第一规则:若y=x,则总压对y的导数等于0。
柯诺洛夫第二规则:若y>x,则总压对y的导数大于0;若y<x,则总压对y的导数小于0。
虽然从式(9)导出了柯诺洛夫规则,但目前的物理化学教科书都很少对此做进一步讨论。柯诺洛夫规则指出了总压与气相中A组分物质的量分数y之间的导数关系,但这背后的物理图像是什么呢?
2 柯诺洛夫规则与相图
上节讨论了柯诺洛夫规则,在这一节将讨论柯诺洛夫规则的实际物理意义,即柯诺洛夫规则与相图的关系。柯诺洛夫第一规则指出,当y=x时,溶液的总蒸气压p对y的偏导数为0。因此,如果以p对y作图,则导数的零点可能对应于气相线的极值点。这一极值点可能为极大值,也可能为极小值,如图1和图2。图1和图2给出了气相线的定性的图像。y=x还意味着在这一点气相线和液相线重合。

图1 柯诺洛夫第一规则(气相线有一极小值)

图2 柯诺洛夫第一规则(气相线有一极大值)
柯诺洛夫第二规则第一条指出,当y>x时,溶液的总蒸气压p对y的偏导数大于0。这说明随着y增加,p也增加,即气相线是单调增加的。另一方面,y>x,又将气相线和液相线联系起来。气相中A组分的物质的量分数y大于液相中A组分的物质的量分数x,这说明液相线总是在气相线的左边,否则不能满足y>x这一条件。这样,由气相线和液相线可以构成一个完整的气液相图(图3)。从图3可以看出,对气相物质的量分数y2,其相应的液相物质的量分数x2应在y2的左边,因为y2>x2。对另一气相组成y1,假设y1<y2,其相应的液相物质的量分数为x1。x1当然也应在y1的左边。但x1究竟是在x2和y1之间,还是在x2的左边呢?还是两者都有可能呢?对此进行分析如下:当y=0和y=1时,x=0和x= 1,即两组分体系变为单组分体系,分别对应于纯B和纯A体系。这意味着气相线和液相线在两个端点重合。因此,一种最简单的情形是,液相线也单调递增。如果液相线单调上升,则x1将在x2的左边。这正好是图3所示的情形。
柯诺洛夫第二规则第二条指出,当y<x时,溶液的总蒸气压p对y的偏导数小于0。与上面的分析类似,可以很容易得出其相应的气液相图如图4所示。

图3 柯诺洛夫第二规则(y增加,p也增加)

图4 柯诺洛夫第二规则(y增加,p减小)
如果将柯诺洛夫第一规则和第二规则结合起来,即考虑气相线还存在极值点的情形,则可得到如图5和图6所示的气液相图。图5对应于气相线存在极小值的情形,图6对应于气相线存在极大值的情形。
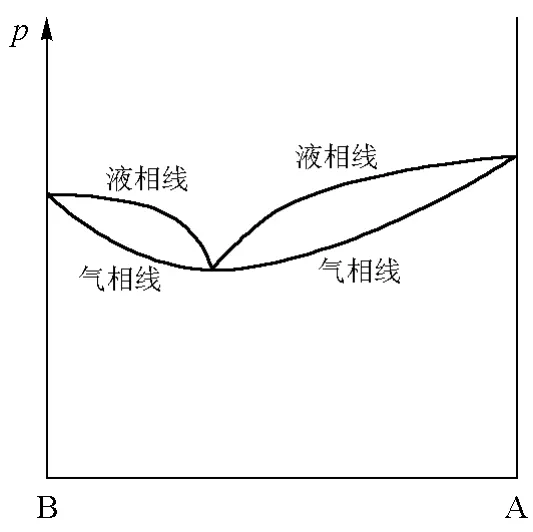
图5 气相线有极小值的气液相图
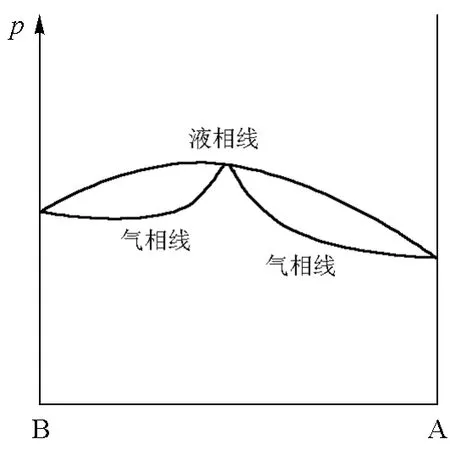
图6 气相线有极大值的气液相图
通过上面的讨论可以看出,柯诺洛夫规则看似简单,实际上蕴藏着非常丰富的物理图像。虽然从柯诺洛夫规则得到的气液相图是定性的,但在物理化学教材的相图部分中都要遇到[2-5]。
3 非理想溶液探讨
第2节采用柯诺洛夫规则从定性的角度讨论了4种可能的气液相图。其实,利用式(9)还可以对此定量地进行分析。在推导式(9)的过程中,曾假定气相为理想气体,即pA=py。如果再假定液相中A组分服从拉乌尔定律,即pA=px(p为纯A的饱和蒸气压),则可得出y和x之间的关系式:

将式(10)代入式(9),得:

对上式两边积分,得:

其中c为积分常数。由于假定气相为理想气体,pB=p(1-y),上式可写成:

将p=pA+pB以及pA=px代入式(11),得:

由于xB=1-x,可以看出,如果假定组分A服从拉乌尔定律,则组分B的分压和它的浓度成正比。如果积分常数c满足下面关系式:

则pB服从拉乌尔定律,即pB=pxB(p为纯B的饱和蒸气压)。另外,如果积分常数c满足下式:

则pB服从亨利定律,即pB=kxxB(kx为亨利常数)。在这两种情况下,气液相图中的液相线均为一直线,p=px+p(1-x),或p=px+kx(1-x),但气相线稍微复杂一些,具体形式如下:

以上讨论了溶液为理想溶液或稀溶液时的情形。如果溶液中组分A不服从拉乌尔定律,为简单起见,可假定其具有如下的二次形式:

其中c为一参数,需由实验确定。又已知pA=py,则p(x+cx2)=py。对等式两边取自然对数,并对y求导数,得:

将式(9)代入式(17),则有:

对式(18)积分,整理后得:


将d的表达式代入式(19),经过进一步整理,得:

由式(20)可求出y的倒数的表达式如下:

对式(20)两边同时除以总压p,得:

已知p*A(x+cx2)=py以及pB=p(1-y),由式(22)可求出pB的表达式如下:

由式(16)和式(23),可得出总压p和液相中A组分物质的量分数x的关系如下:

如果参数c已知,则由式(24)可以作出气液相图中的液相线。对于给定的总压p和相应的x,由式(21)可计算出相应的y,进而可作出相应的气相线。这样,就得到了完整的气液相图。
从式(16)和式(23)可看出,组分A和B都不满足拉乌尔定律,它们的活度系数分别如下:

已知活度系数γA和γB之间存在如下关系式[2]:

式(25)的正确性可以通过式(26)加以验证。
4 结论
本文以式(9)和柯诺洛夫规则为例,讨论如何引导学生思考问题,培养学生分析问题的能力。式(9)和柯诺洛夫规则看似简单,但其背后却蕴藏着丰富的物理图像,即气液相图。式(9)不仅可以帮助我们分析理想溶液和稀溶液中总蒸气压和气液相中A组分浓度之间的定量关系,而且作为一个有力的工具,还可以帮助我们向前迈出一步,进入非理想溶液领域,从而定量地讨论非理想溶液中的气液相图。这样的例子还有很多。如果这些例子能启发大学生自己去探索、去挖掘某些问题背后的物理本质,不管这些问题有多重要,或无足轻重,则我们培养他们分析问题能力的目的就达到了。
[1]高新秀,陈飞武,王桂华,等.物理化学教学中研究式教学方法//张欣欣.实践与创新——北京科技大学本科教育教学改革论文集.北京:高等教育出版社,2007:149-153
[2]傅献彩,沈文霞,姚天扬,等.物理化学.第5版.北京:高等教育出版社,2009
[3]韩德刚,高执棣,高盘良.物理化学.第2版.北京:高等教育出版社,2009
[4]Levine I N.Physical Chemistry.5th ed.NewYork:McGraw-Hill,2002
[5]Atkins P,Paula J.Atkins's Physical Chemistry.7th ed.London:Oxford University Press,2006
北京科技大学研究型示范教学项目
**通讯联系人,E-mail:chenfeiwu@ustb.edu.cn

