一种新的无轴承永磁同步电机径向悬浮力研究方法

国网湖北省电力公司神农架供电公司 汪泉 汪明涛

1 引言

随着现代农业科技、电力电子技术、微电子技术、新型电机控制理论和稀土永磁材料的快速发展，使得永磁同步电动机在离心泵、机械加工、干燥机、高精数控机床等领域得以迅速的推广应用。永磁同步电机与传统的电励磁同步电机相比，效率高、损耗少、节电效果明显，这些优点在稀土永磁同步电机上表现的尤为显著，因而它成为了近年来广受研究并在各个领域中广泛应用的一种电动机[1]。无轴承永磁同步电机充分利用了磁轴承与电机产生电磁力原理的相似性，把磁轴承中产生径向力的绕组安装在电机定子上，通过解耦控制，独立控制了电机转矩和径向悬浮力。无轴承电机被广泛应用于需要免维修、长寿命运行，无菌、无污染以及有毒有害液体或气体的传输等场合[2-3]。因此，研究无轴承永磁同步电机是非常有价值的。

基于迦辽金加权余量法或变分原理的有限元法，最早用于力学计算中[4]，其具有以下优点：系数矩阵对称、正定且具有稀疏性，几何剖分灵活，有利于分析几何形状复杂的问题；适宜于处理非线性问题。本文在基于电磁场理论基础上推导出无轴承永磁同步电机径向悬浮力数学模型。基于有限元的优点，在Ansoft/Maxwell有限元分析软件基础上，提出了一种简单的气隙磁密基波法对无轴承永磁同步电机径向悬浮力数学模型进行研究验证，仿真结果验证了径向悬浮力数学模型的正确性。

2 径向悬浮力数学模型

忽略洛仑磁力和由于转子偏心而引起的径向作用力。不计电机磁饱和、涡流损耗与齿槽效应。假定铁芯和气隙的磁导率分别为μFe与μ0，并且μFe远大于μ0，铁芯与气隙交界面上的法向磁感应强度和切向磁场强度分别为Bm，Hm，由于Hm≈0，作用在转子表面面积为元dA上的麦克斯韦力可表示为:

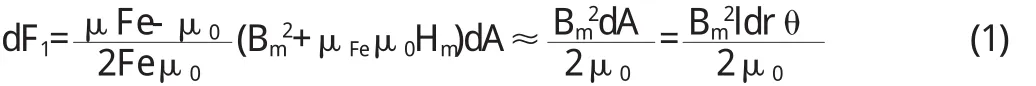
式中，μ0=4×10-7H/m，l为铁芯长度，r为转子外半径，θ为空间位置角。气隙中的合成磁密为:

其中，B1，B2分别为永磁体、转矩绕组共同产生的气隙磁密幅值和径向悬浮力绕组单独产生的气隙磁密基波幅值；μ、λ为初始相位角；ω1、ω2为转矩绕组和径向悬浮力绕组的电角频率。

可将转子表面单位面积上的径向悬浮力写成：dF(θ,t)=

将上式沿圆周积分，得径向悬浮力沿x方向上的分量为：

其中，P1=1，P2=2，ω1=ω2。

同样的可得到径向悬浮力沿y方向上的分量为：

分析Fx和Fy的公式可知，Fx正好为一余弦函数，而Fy为一正弦函数，令它们的幅值为：

分析(6)可得，若能获得气隙磁密幅值B1和B2便能得到Fr的值。

3 电机的有限元模型与磁场分析

参数：P1=1，P2=2，转矩绕组的额定电流为10A，径向悬浮力绕组的额定电流为10A，定子槽数12，定子铁芯外径155mm，定子铁芯内径98mm，转子外径93mm，转子内径50mm，铁芯长度135mm，转矩绕组和径向悬浮力绕组每槽匝数为40，转速3000rpm。

定子槽分成内层和外层两部分，分别嵌入径向悬浮力绕组和转矩绕组。图1为电机磁力线分布图。左边为只加转矩绕组电流时磁力线呈两极对称分布；中图表示的是只加径向悬浮力绕组电流时磁力线呈四极对称分布；右图为两绕组同时通过三相对称电流时合成磁力线分布，可以看出磁力线密集的位置位于y轴的负方向上，而y轴正方向上的磁力线则很稀疏，根据电磁场麦克斯韦力产生原理，可知电机沿y轴负方向产生了径向悬浮力。

图1 磁力线分布

4 径向悬浮力的有限元值和数学模型值

同时给转矩绕组和径向悬浮力绕组通以10A额定三相对称交流电时，在Ansoft/Maxwell中Fx和Fy的有限元波形曲线分别如图2所示。由图可知Fx为一余弦曲线，而Fy为一正弦曲线，与径向悬浮力数学模型分析结果一致。从图中读取其幅值记作Ft=280N。

图2 有限元波形

由前面分析得知，径向悬浮力的数学模型值的求取可转换成对B1和B2的求取，结合公式便能得到径向悬浮力的数学模型幅值。

当转矩绕组电流为额定值10A，径向悬浮力绕组不通电时，气隙磁密波形和进行FFT分解后的波形分别如图3所示。

图3 转矩绕组气隙磁密波形

根据图3，电机气隙磁密的基波幅值B1=0.18T。

当径向悬浮力绕组电流为额定值10A，转矩绕组电流不通电时，气隙磁密波形和进行FFT分解后的波形分别如图4所示。

图4 各次谐波波形

根据图4，电机气隙磁密的基波幅值为B2=0.2T。

将B1、B2与其它已知量代入公式(6)中，得Fr=282.5N。

5 径向悬浮力的的比较分析

当转矩绕组和径向悬浮力绕组分别通以10A额定三相对称交流电时，径向悬浮力的有限元模型值Ft和数学模型值Fr之间的误差很小，它们基本相等。即Fx、Fy的有限元波形与数学模型是一致的。接下来分析一般情况：

当转矩绕组电流保持额定值10A不变，Ft和Fr随径向悬浮力绕组电流的变化情况如下表所示。

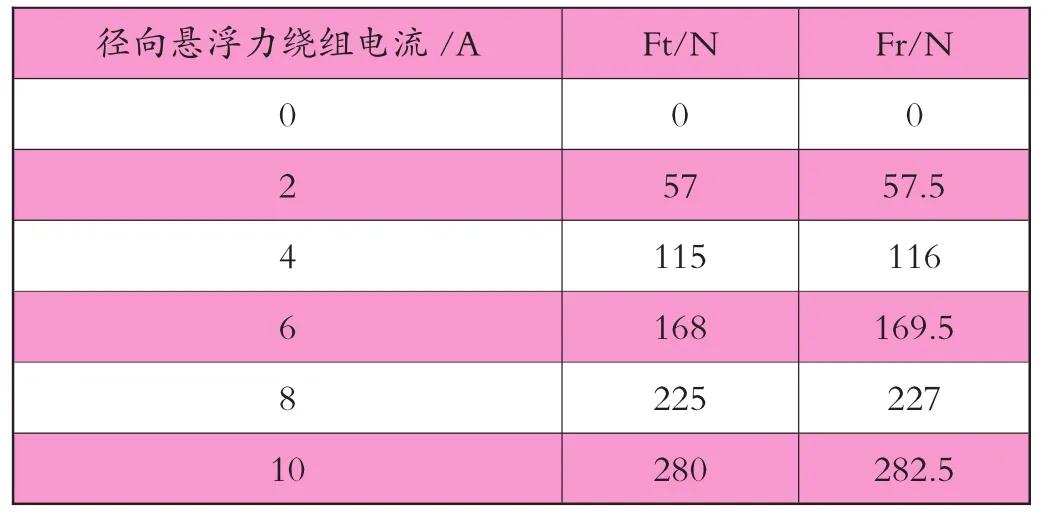
表1 径向悬浮力随径向悬浮力绕组电流变化的取值

将表1中的数据在Matlab中进行曲线拟合，可得曲线图5。

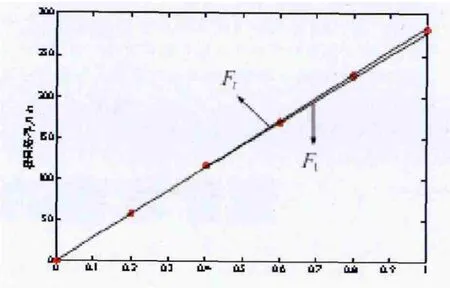
图5 径向悬浮力的比较

由图5中的曲线对比可知，随着径向悬浮力绕组电流的增大，Ft和Fr基本上呈线性增加，两者数值基本相等，误差极小。且Ft比Fr略小，造成这种现象的原因是Ansoft综合考虑了磁饱和，定子磁势谐波、涡流损耗和齿槽效应等因素。通过有限元分析证明了径向悬浮力数学模型是正确的，为无轴承永磁同步电机的优化设计提供了理论依据。

6 结论

本文使用了有限元的研究方式，控制绕组电流，进而分析了无轴承永磁同步电机的内部磁场，证明了径向悬浮力产生原理是正确的。此外，还运用简单的基波幅值法研究了径向悬浮力的数学模型，与有限元仿真数值与数学模型计算值相结合，从而使径向悬浮力数学模型的正确性和有效性得到了验证。为无轴承永磁同步电机的进一步优化提供了借鉴。

[1]吴钦木,韦书龙,李捍东等.永磁同步电机驱动系统效率优化控制参数变化影响研究[J].电机与控制应用,2012,39(6):18-23.

[2]A.C hiba,J.A sama.I nfluence of rotor skew in induction type bearingless motor[J].I EEE T ransactions on M agnetics,2012,48(11):4646-4649.

[3]D.C.F ei,H.Q.Z hu.Study on decoupling control of bearingless permanent magnet synchronous motors based on inverse system theory[J].Engineering Science,2005,7(11)48-54.

[4]朱熀秋，张涛.无轴承永磁同步电机有限元分析[J].中国电机工程学报,2006,26(3):136-140.